
W ramach drugiego wykładu z baz danych zostanie przedstawiony relacyjny model danych, który w praktyce jest najczęściej stosowany. W szczególności wykład omówi: struktury danych tego modelu, operacje modelu i ograniczenia integralnościowe.


W ogólności model danych definiuje:
- struktury wykorzystywane do reprezentowania danych,
- operacje na danych,
- ograniczenia integralnościowe, czyli reguły poprawności danych.
Jednym z fundamentalnych modeli jest model relacyjny. Jest on wykorzystywany w większości komercyjnych i niekomercyjnych systemów baz danych. W modelu tym, strukturą danych jest relacja; operacje na danych obejmują selekcję, projekcję, połączenie i operacje na zbiorach. Ograniczenia integralnościowe w tym modelu to: klucz podstawowy, klucz obcy, zawężenie dziedziny, unikalność wartości, możliwość nadawania wartości pustych/niepustych.

Każdy atrybut posiada swoją domenę, zwaną także dziedziną. Definiuje ona zbiór wartości jakie może przyjmować atrybut poprzez określenie tzw. typu danych, np. liczba całkowita, data, ciąg znaków o długości 30.

Relacją r o schemacie R(A1, A2, ..., An), oznaczoną r(R), nazywamy zbiór n-tek (krotek) postaci r={t1, t2, ..., tm}.
Pojedyncza krotka t jest uporządkowaną listą n wartości t=<v1, v2, ..., vn>, gdzie vi, 1<i<n, jest elementem dom(Ai) lub specjalną wartością pustą (NULL).
i-ta wartość krotki t, odpowiadająca wartości atrybutu Ai, będzie oznaczana przez t[Ai].
Matematyczna definicja relacji jest następująca:
Relacja r(R) jest relacją matematyczną stopnia n zdefiniowaną na zbiorze domen dom(A1), dom(A2), ..., dom(An) będącą podzbiorem iloczynu kartezjańskiego domen definiujących R.
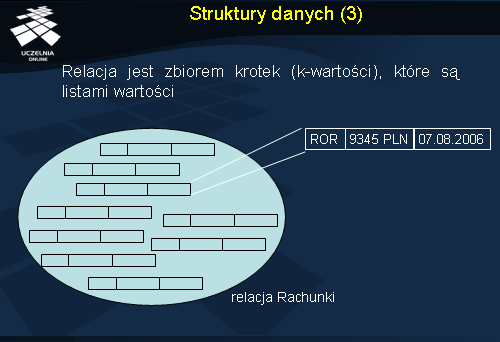


Baza danych jest zbiorem relacji.
Schemat relacji jest zbiorem {atrybut, dziedzina, [ograniczenia integralnościowe]}.
Schemat bazy danych jest zbiorem schematów relacji.
Relacja jest zbiorem krotek.
Krotka jest listą wartości atomowych.

Relacja posiada następujące cechy:
- każdy atrybut relacji ma unikalną nazwę,
- porządek atrybutów w relacji nie jest istotny,
- porządek krotek w relacji nie jest istotny i nie jest elementem definicji relacji,
- wartości atrybutów są atomowe (elementarne),
- relacja nie zawiera rekordów powtarzających się. Ponieważ relacja jest zbiorem krotek, więc, z definicji zbioru, wszystkie krotki relacji muszą być unikalne.


Klucz jest minimalnym superkluczem zachowującym własność unikalność krotek relacji.
Schemat relacji może posiadać więcej niż jeden klucz.


Wyróżnia się następujące ograniczenia integralnościowe:
- klucz podstawowy (primary key),
- klucz obcy (foreign key),
- unikalność (unique),
- zawężenie domeny/dziedziny (check),
- wartość pusta/niepusta (NULL/NOT NULL).

Przykładami atrybutów, które mogły by być kluczami podstawowymi są np. adres e-mail, NIP, PESEL, nr dowodu, nr paszportu.
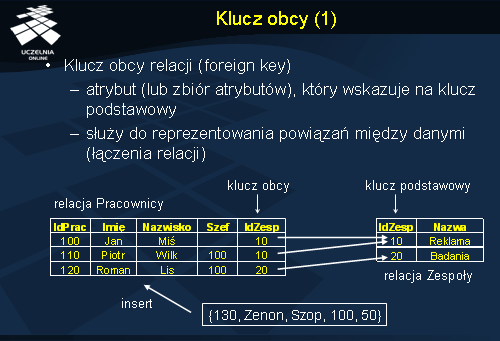
W przykładzie ze slajdu, w relacji Zespoły kluczem podstawowym jest atrybut IdZesp. W relacji Pracownicy kluczem obcym jest IdZesp i wskazuje on na IdZesp w relacji Zespoły. Wartościami atrybutu IdZesp w relacji Pracownicy mogą być tylko te wartości, które przyjmuje IdZesp w relacji Zespoły.
Przykładowy rekord {130, Zenon, Szop, 100, 50} nie zostanie wstawiony do relacji Pracownicy, ponieważ wartość atrybutu IdZesp (50) nie znajduje się w relacji Zespoły. Naruszono w tym przypadku ograniczenie integralnościowe klucza obcego.

Dane są relacje R1 i R2. Podzbiór FK atrybutów relacji R1 nazywany jest kluczem obcym R1 jeżeli:
- atrybuty w FK mają taką samą domenę jak atrybuty klucza podstawowego PK relacji R2,
- dla każdej krotki t1 relacji R1 istnieje dokładnie jedna krotka t2 relacji R2, taka że t1 [FK] = t2 [PK], lub t1 [FK] = null.
Klucz obcy, zwany również ograniczeneim referencyjnym, gwarantuje, że rekordy z tabeli R1 występują w kontekście związanego z nim rekordu z tabeli R2.

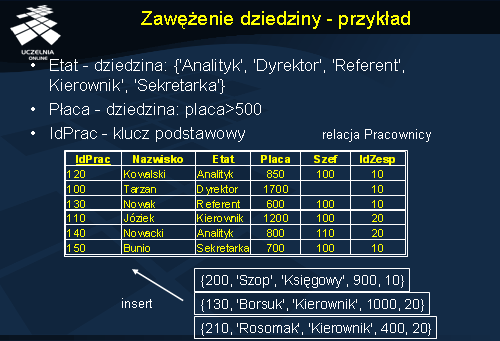
Zbiór wartości domeny atrybutu może być zawężony przez wyrażenie logiczne do pewnego podzbioru: przedziału lub wyliczeniowej listy wartości. Jest to tzw. ograniczenie integralnościowe zawężenia dziedziny (domeny). Przykładami tego typu ograniczenia są np.
- ograniczenie dopuszczalnych wartości atrybutu płeć do: K, M, nieznana, N/A (zgodnie ze standardem ISO),
- zagwarantowanie dodatnich wartości atrybutu pensja,
- ograniczenie dopuszczalnych wartości atrybut kolor_oczu do trzech wartości: niebieskie, szare, piwne.


Operacja ta jest oznaczana symbolem sigma z pewnym warunkiem selekcji. Operacja ta działa na relacji o pewnej nazwie. Warunek selekcji jest zbiorem predykatów postaci <atrybut><operator relacyjny><literał> lub <atrybut><operator relacyjny><atrybut>.
Predykaty są łączone operatorami logicznymi: AND lub OR.
Rozważmy dwie operacje selekcji. Operacja S1 jest realizowana jako pierwsza. S1 posiada warunek W1 i jest realizowana na relacji R. Operacja S2 jest realizowana jako druga. S2 posiada warunek W2 i jest realizowana na wyniku operacji S1. Przyjmijmy, że wynik operacji S1 i S2 wykonanych w takiej kolejności jest zbiorem krotek {k1, k2, k3}. Jeżeli zamienimy kolejność wykonywania operacji selekcji, tzn. najpierw zostanie wykonana operacja S2 z warunkiem W2 na relacji R, a następnie S1 z warunkiem W1 na wyniku działania operacji S2, to w wyniku końcowym otrzymamy identyczny zbiór krotek jak poprzednio. Taką własność operacji selekcji nazywamy komutatywnością.

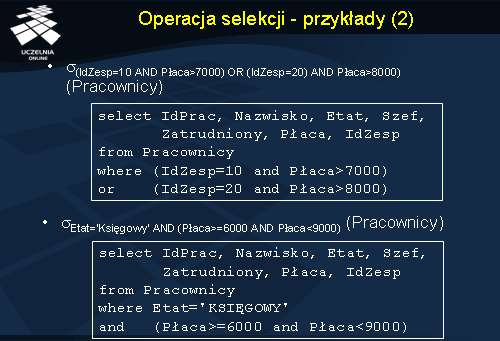
Drugi przykład ilustruje selekcję z relacji Pracownicy wszystkich księgowych zarabiających w przedziale między 6000 i 9000.

Operacja ta jest oznaczana symbolem pi z podzbiorem wybieranych atrybutów z całego zbioru atrybutów relacji. Operacja ta działa na relacji o pewnej nazwie.
Operacja projekcji nie jest komutatywna, a składanie operacji projekcji jest możliwe jeżeli lista2 zawiera wszystkie atrybuty lista1. Notację operacji składania projekcji przedstawiono na slajdzie.

Obie przykładowe operacje projekcji wyrażono w notacji ogólnej i w języku SQL.

Jako przykład rozważmy operację selekcji z warunkiem IdZesp=10. Przyjmijmy, że jej wynikiem jest relacja tymczasowa o nazwie PracZesp10. Następnie na tej relacji wykonujemy operację projekcji atrybutów IdPrac i Nazwisko. Przyjmijmy, że jej wynikiem jest relacja tymczasowa o nazwie PracZesp10Wynik.
Obie operacje można złożyć w jedną, której wynik będzie identyczny z zawartością relacji PracZesp10Wynik, jak pokazano na slajdzie.

Dwie relacje są kompatybilne jeśli mają ten sam stopień i dziedziny odpowiadających sobie atrybutów są takie same.
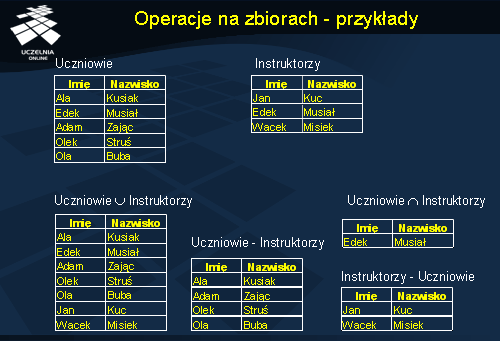
Operacje sumy, iloczynu i różnicy dwóch kompatybilnych relacji R i S są zdefiniowane następująco.

Iloczyn: wynikiem tej operacji, oznaczonej przez R ILOCZYN S, jest relacja zawierająca krotki występujące zarówno w R i S. Operacja iloczynu jest operacją komutatywną: R ILOCZYN S = S ILOCZYN R.



Dane są dwie relacje: R(A1, ..., An) i S(B1, ...,Bm). Wynikiem iloczynu kartezjańskiego relacji R i S, oznaczonym przez R x S, jest relacja Q stopnia n+m i schemacie: Q(A1, ..., An, B1, ...,Bm). Krotkom w relacji Q odpowiadają wszystkie kombinacje krotek z relacji R i S. Jeżeli relacja R ma N krotek, a relacja S ma M krotek, to relacja Q będzie miała M*N krotek. Innymi słowy, iloczyn kartezjański polega na połączeniu każdej krotki z relacji R z każdą krotką relacji S.


Notację operacji łączenia relacji R i S przedstawiono na slajdzie. Warunek połączeniowy jest zbiorem predykatów połączonych operatorami logicznymi AND. Predykaty te są postaci: Ai THETA Bj, gdzie
- Ai i Bj są atrybutami połączeniowymi,
- Ai jest atrybutem R, Bj jest atrybutem S,
- dom(Ai) = dom(Bj),
- THETA jest operatorem relacyjnym ze zbioru { =, !=, <, >, <=, >= }.

Operacja połączenia, dla której THETA jest operatorem =, nazywana jest połączeniem równościowym (ang. equi join).
Operacja połączenia, dla której THETA jest operatorem różnym od =, nazywana jest połączeniem nierównościowym (ang. non-equi join).

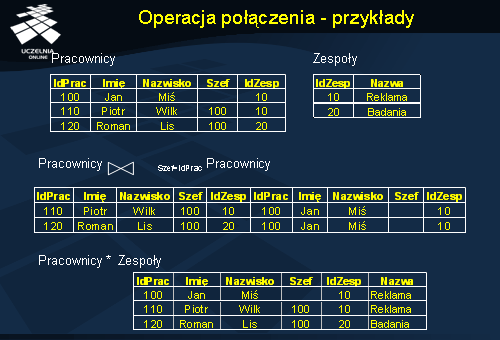

Połączenie równościowe zapisano w dwóch postaciach, pierwsza nie jest zgodna ze standardem SQL, ale jest wspierana przez wiele SZBD. Druga notacja jest zgodna ze standardem języka. Połączenie naturalne wyspecyfikowano zgodnie ze standardem.