Algorytmy odkrywania binarnych reguł asocjacyjnych

Celem naszego wykładu jest zapoznanie się z dwoma podstawowymi algorytmami odkrywania binarnych reguł asocjacyjnych, najczęściej wykorzystywanymi w praktyce, algorytm A-priori oraz algorytm FP-Growth. Przeanalizujemy przykłady z zastosowaniem powyższych algorytmów.


Algorytm Apriori



Pierwszym algorytmem odkrywania binarnych reguł asocjacyjnych, który wykorzystał własność monotoniczności miary wsparcia do ograniczenia przestrzeni poszukiwań zbiorów częstych, był algorytm Apriori. Algorytm ten jest algorytmem iteracyjnym, który w kolejnych krokach (iteracjach) znajduje zbiory częste o rozmiarach 1, 2, ..., k. Zakładamy, że elementy każdej transakcji ze zbioru D są uporządkowane leksykograficznie {Jeżeli nawet transakcje nie są wewnętrznie posortowane, to krokiem wstępnym algorytmu może być leksykograficzne uporządkowanie elementów transakcji.}. Pierwszym krokiem algorytmu jest wyodrębnienie z bazy danych D wszystkich zbiorów jednoelementowych, które występują w transakcjach, i sprawdzenie, które z nich są częste (posiadają wsparcie co najmniej minsup). Następnie, w oparciu o zbiory częste jednoelementowe algorytm generuje zbiory kandydujące (ang. candidate itemsets) dwuelementowe, które, potencjalnie mogą być zbiorami częstymi. Dla każdego wygenerowanego zbioru kandydującego obliczane jest jego wsparcie w bazie danych D. Jeżeli obliczone wsparcie zbioru kandydującego wynosi co najmniej minsup, to jest on dołączany do listy zbiorów częstych i w kolejnym kroku zostanie on wykorzystany do generacji zbiorów kandydujących trzyelementowych. Następnie, zbiory częste trzyelementowe są wykorzystywane do generacji zbiorów kandydujących czteroelementowych, zbiory częste czteroelementowe są wykorzystywane do generacji zbiorów kandydujących pięcioelementowych, itd. W każdym kolejnym kroku, w oparciu o zbiory częste znalezione w poprzednim kroku, algorytm generuje zbiory kandydujące o rozmiarze większym o 1. W celu obliczenia wsparcia zbiorów kandydujących, w każdym kroku algorytmu jest dokonywany odczyt bazy danych D. Działanie algorytmu się kończy, gdy nie ma można już wygenerować kolejnych zbiorów kandydujących. Wynikiem działania algorytmu jest suma k-elementowych zbiorów częstych (k=1, 2,...).


Algorytm 1.3 Apriori



W opisie algorytmu zastosowano następującą notację: C_k oznacza rodzinę zbiorów kandydujących k-elementowych, L_k oznacza rodzinę zbiorów częstych k-elementowych, c.count oznacza licznik zliczający liczbę transakcji wspierających zbiór elementów c, apriori_gen () oznacza funkcję, opisaną na kolejnym slajdzie, która generuje zbiory kandydujące, natomiast subset() oznacza funkcję, która dla danej transakcji t zwraca wszystkie zbiory kandydujące wspierane przez t. W pierwszym kroku algorytm zlicza wystąpienia wszystkich elementów w bazie danych D w celu wyodrębnienia zbiorów częstych 1-elementowych (L_1). Każdy kolejny k-ty krok algorytmu składa się z dwóch faz. W pierwszej, funkcja apriori_gen(), w oparciu o zbiory częste należące do L_{k-1}, generuje zbiory kandydujące k-elementowe (C_k). W drugiej fazie k-tego kroku jest realizowany odczyt bazy danych D i dla każdego zbioru kandydującego c ze zbioru C_k jest obliczane wsparcie zbioru c w bazie danych D, {wsparcie}(c). W celu zapewnienia odpowiedniej efektywności procedury obliczania wsparcia zbiorów kandydujących, algorytm Apriori wykorzystuje strukturę danych postaci drzewa haszowego, która służy do przechowywania zbiorów kandydujących. Procedura subset() zwraca te zbiory kandydujące należące do C_k, które są wspierane przez transakcję t.


Jeżeli zbiór kandydujący c spełnia warunek minimalnego wsparcia, to jest, {wsparcie}(c)>= minsup, to zbiór ten jest dodawany do listy zbiorów częstych, w przeciwnym razie zbiór ten jest usuwany z listy zbiorów kandydujących. Podstawowe znaczenie dla efektywności działania algorytmu Apriori ma rozwiązanie dwóch problemów szczegółowych: jak zapewnić efektywność procedury generowania zbiorów kandydujących, oraz, jak zapewnić efektywność procedury obliczania wsparcia dla tych zbiorów. Pierwszy z wymienionych problemów dotyczy efektywności funkcji apriori_gen().



Funkcja Apriori_Gen(Ck)



Funkcja apriori_gen() jest realizowana w dwóch krokach: (1) kroku generacji zbiorów kandydujacych (ang. join step) oraz (2) kroku usuwania zbiorów kandydujacych (ang. prune step). W kroku pierwszym, zbiory kandydujace k-elementowe (Ck) sa generowane poprzez łaczenie zbiorów czestych (k-1)-elementowych (Lk-1). W kroku drugim, ze zbioru Ck sa usuwane te zbiory kandydujace, których jakikolwiek podzbiór nie jest zbiorem czestym. Zło_onosc pierwszego kroku funkcji apriori_gen(), dla i-tej iteracji, w najgorszym przypadku, jest rzedu O(|Li| ^2). Wynika ona z koniecznosci znalezienia wszystkich par zbiorów (ci, cj) nale_acych do Lk-1, takich, _e ich suma daje zbiór o rozmiarze i. Krok drugi funkcji apriori_gen() wymaga sprawdzenia, czy utworzony zbiór jest rzeczywiscie zbiorem kandydujacym, to znaczy, wymaga sprawdzenia, czy ka_dy podzbiór tego zbioru jest zbiorem czestym. Ta procedura wymaga sprawdzenia |Li| zbiorów. Stad, zło_onosc obliczeniowa funkcji apriori_gen() jest rzedu O(Si |Li|^3). W praktyce, rzadko mamy do czynienia z najgorszym przypadkiem, gdy_, najczesciej, niewiele zbiorów czestych posiada k-1 wspólnych elementów, co pozwala na ich łaczenie. Zauwa_my równie_, _e przedstawiona zło_onosc obliczeniowa funkcji apriori_gen jest niezale_na od liczby transakcji n. Wynika to z faktu, _e generowanie zbiorów kandydujacych nie wymaga dostepu do bazy danych, lecz wykorzystuje do tego celu odkryte wczesniej zbiory czeste. Drugi ze wspomnianych problemów dotyczy efektywnosci procedury obliczania wsparcia dla wygenerowanych przez funkcje apriori_gen zbiorów kandydujacych. Załó_my, _e dany jest zbiór Ci, którego elementami sa zbiory kandydujace o rozmiarze i. Obliczenie wsparcia zbiorów kandydujacych ze zbioru Ci wymaga tylko jednokrotnego odczytu bazy danych D. Wystarczy bowiem dla ka_dego zbioru kandydujacego c utworzyc licznik, c.count, który bedzie zliczał liczbe transakcji wspierających zbiór c. Zło_onosc obliczeniowa przedstawionej procedury obliczania wsparcia dla zbioru Ci jest rzedu O(|Ci|nq), gdzie n oznacza liczba transakcji w bazie danych D, natomiast q oznacza maksymalny rozmiar transakcji nale_acej do D. Algorytm Apriori wymaga k lub k+1 odczytów bazy danych D, gdzie k oznacza maksymalny rozmiar zbioru czestego.



Przykład 1



Powyższy przykład ilustruje działanie algorytmu Apriori. Rozważmy przykładową bazę danych produktów przedstawioną na slajdzie w w postaci znormalizowanej relacji. W relacji mamy transakcje ze sprzedaży 5 produktów. Transakcja określona jest przez TID, który jest identyfikatorem transakcji oraz produktów, które w ramach danej transakcji zostały zakupione. Załóżmy wartość minimalnego wsparcia = 50% (2 transakcje z 4 możliwych). Dla uproszczenia w podanych tabelach wsparcie zbioru jest liczone w transakcjach.

Pierwszy krok algorytmu polega na znalezieniu wszystkich zbiorów kandydatów zbiorów częstych 1-elementowych C1 i sprawdzeniu czy spełniają minimalny próg wsparcia. Otrzymaliśmy w ten sposób zbiór L1 wszystkie zakupione produkty poza 4 są wspierane przez co najmniej 2 transakcje, zatem, każdy produkt z wyłączeniem 4, stanowi zbiór częsty 1-elementowy.





Następnie, w kolejnym kroku algorytmu, funkcja apriori-gen() generuje zbiory kandydujące 2-elementowe C2 uzyskane w oparciu o L1. Na powyższym slajdzie możemy zobaczyć zbiór C2, wraz z wartościami wsparcia poszczególnych zbiorów kandydujących. Zbiór L2 składa się z tych zbiorów kandydujących 2-elementowych należących do C2, których wsparcie spełnia warunek minimalnego wsparcia minsup. Pamiętamy w naszym przykładzie wynosi on 50% (2 transakcje). W kolejnym kroku, funkcja apriori-gen() generuje zbiory kandydujące 3-elementowe C3 w oparciu o L2. Każdy zbiór kandydujący 3-elementowy jest nadzbiorem zbioru częstego 2-elementowego należącego do L2, i każdy jego podzbiór również należy do L2. C3 zawiera tylko jeden zbiór kandydujący. Wygenerowany zbiór kandydujący jest również zbiorem częstym, gdyż jego wsparcie wynosi 2 stąd pojawia się on w zbiorze L3. Zbiór C4 jest zbiorem pustym, gdyż L3 zawiera tylko jeden zbiór częsty. Stąd L4 również jest zbiorem pustym. Kończy to pierwszy etap algorytmu Apriori. Wynikiem tego etapu są zbiory częste 1-elementowe L1, 2-elementowe L2, oraz 3-elementowe L3. W kolejnym etapie, w oparciu o otrzymane zbiory częste, są generowane binarne reguły asocjacyjne zgodnie z algorytmem 1.2. Na etapie generacji reguł pomijamy zbiory częste 1-elementowe, gdyż prowadziłyby one do reguł asocjacyjnych, których poprzednik lub następnik byłby zbiorem pustym.


Generacja zbiorów kandydujących



Jak wcześniej pokazano, jednym z głównych operacji wykorzystywanych w algorytmie Apriori jest generacja zbiorów kandydujących. Przyjrzyjmy się dokładniej tej operacji. Mamy daną kolekcję zbiorów częstych k-elementowych – Lk. Generacja zbiorów kandydujących realizowana jest w dwóch krokach. W pierwszym kroku następuje połączenie (zbiór Lk1 ze zbiorem Lk2) z następującym warunkiem połączeniowym – pierwszych k-1 elementów musi być identycznych oraz Lk1[k]<Lk2[k]. Gdzie lki[k] oznacza k-ty element zbioru Lki.


Drugi krok – odcięcie, polega na usunięciu wszystkich zbiorów kandydujących, które posiadają nieczęste podzbiory.





Generację zbiorów kandydujących możemy prześledzić na powyższym przykładzie. Dana jest kolekcja w postaci zbioru L2. Wykonujemy pierwszy krok generacji zbiorów kandydujących – połączenie. W wyniku czego otrzymujemy zbiór C3. Następnym krokiem generacji zbiorów kandydujących jest odcięcie czyli usunięcie wszystkich zbiorów kandydujących, które posiadają nieczęste podzbiory. W tym przypadku, będzie to zbiór {3 5 7}. Ostateczna postać zbioru C3 po odcięciu, zawiera pojedynczą transakcję, która zawiera kandydata na zbiór częsty.


Idea algorytmu


Podstawowe znaczenie dla poprawy efektywności algorytmu znajdowania zbiorów częstych ma spostrzeżenie, że miara wsparcia zbioru elementów ma własność monotoniczności. Monotoniczność miary wsparcia zbioru oznacza, że zbiór X jest zbiorem częstym wtedy i tylko wtedy, gdy wszystkie podzbiory zbioru X są również zbiorami częstymi. Innymi słowy, jeżeli zbiór X nie jest zbiorem częstym, to żaden nadzbiór zbioru X nie jest zbiorem częstym. Oznacza to, że nie musimy rozważać wsparcia zbioru X, którego podzbiór nie jest zbiorem częstym. Tę własność monotoniczności miary wsparcia można wykorzystać do redukcji przestrzeni poszukiwań zbiorów częstych.


Własność Apriori



Podzbiory zbioru L, ze względu na relację zawierania się, tworzą kratę, której kresem dolnym jest zbiór pusty, natomiast kresem górnym jest cały zbiór L. Przykładową kratę podzbiorów zbioru L = {A,B,C,D}. Podstawowe znaczenie dla poprawy efektywności algorytmu znajdowania zbiorów częstych ma spostrzeżenie, że miara wsparcia zbioru elementów ma własność monotoniczności o której wspomnieliśmy wcześniej. A co się z tym wiąże, nie musimy rozważać wsparcia zbioru X, którego podzbiór nie jest zbiorem częstym. Dlatego skoro podzbiory {ABCD}, {ABD} oraz {ACD} nie są częste stąd zbiór {AD} również nie jest częsty. Własność ta znacznie redukuje przestrzeń poszukiwań podczas generacji częstych kandydatów.


Idea algorytmu



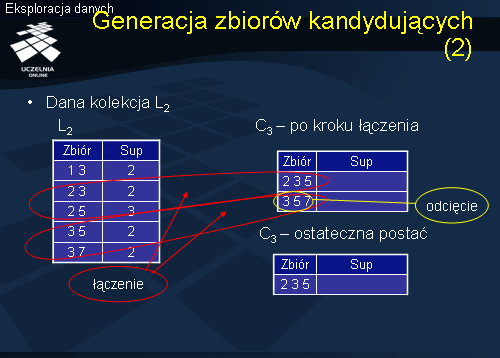
Na podstawie tego co zostało powiedziane wcześniej możemy sformułować ideę algorytmu, że krok połączenia jest równoważny dodaniu do każdego zbioru częstego należącego do Lk, kolejno, każdego elementu z bazy danych, a następnie, usunięciu tych zbiorów kandydujących Ck+1, dla których podzbiór (C[2], C[3], ... ,C[k+1]) nie jest częsty, co wcześniej zostało pokazane na przykładzie.



Generacja reguł



W kolejnym etapie, w oparciu o otrzymane zbiory częste, są generowane binarne reguły asocjacyjne zgodnie z algorytmem 1.3. Na etapie generacji reguł pomijamy zbiory częste 1-elementowe, gdyż prowadziłyby one do reguł asocjacyjnych, których poprzednik byłby zbiorem pustym. Ostatnią fazą algorytmu jest sprawdzenie, które z wygenerowanych reguł spełniają warunek minimalnej ufności minconf. Reguły, których ufność jest mniejsza od minconf są odrzucane.


Przykład 2



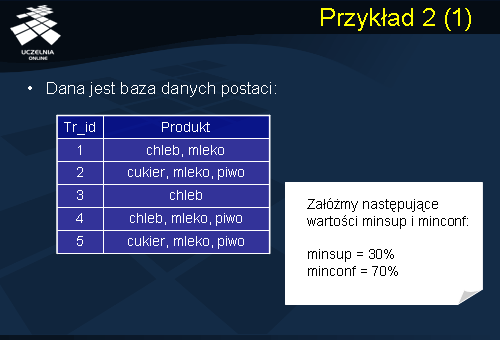
Aby prześledzić dokładnie ścieżkę algorytmu Apriori przeanalizujmy drugi przykład. Mamy daną bazę danych zawierającą dane ze sprzedaży produktów. Zakładamy próg minimalnego wsparcie = 30% natomiast minimalnej ufności = 70%.




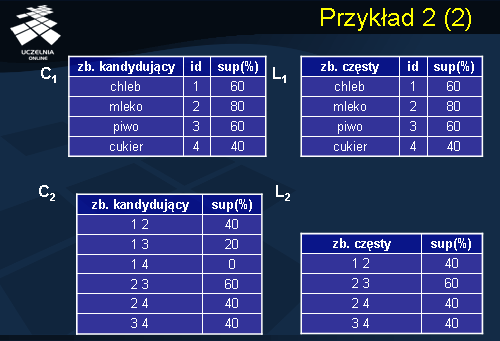
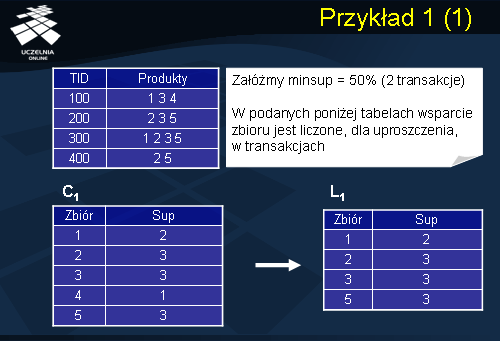
Jak pamiętamy z przykładu wcześniejszego pierwszy krok algorytmu polega na znalezieniu wszystkich zbiorów kandydatów zbiorów częstych 1-elementowych C1 i sprawdzeniu czy spełniają minimalny próg wsparcia. Otrzymaliśmy w ten sposób zbiór L1, w którym znalazły się wszystkie zakupione produkty, zatem, każdy produkt stanowi zbiór częsty 1-elementowy. Następnie generujemy zbiór kandydatów 2-elementowych w oparciu o zbiór L1. (jak wcześniej omówiliśmy generacja składa się z połączenia oraz odcięcia czyli usunięciu wszystkich zbiorów kandydujących, które posiadają nieczęste podzbiory). Po sprawdzeniu wsparcia, otrzymujemy zbiór częsty L2, 2-elementowych produktów.




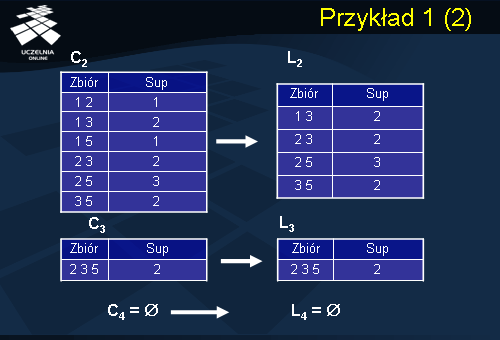
W następnym kroku zostaje wygenerowany zbiór częstych kandydatów C3, analogicznie jak w krokach wcześniejszych otrzymujemy z niego zbiór częsty 3-elementowy. Zbiór C4 jest zbiorem pustym, gdyż L3 zawiera tylko jeden zbiór częsty. Stąd L4 również jest zbiorem pustym. Kończy to pierwszy etap algorytmu Apriori. Wynikiem tego etapu są zbiory częste 1-elementowe L1, 2-elementowe L2, oraz 3-elementowe L3. W kolejnym etapie, w oparciu o otrzymane zbiory częste, są generowane binarne reguły asocjacyjne zgodnie z algorytmem.



Przykład 2 - generacja reguł



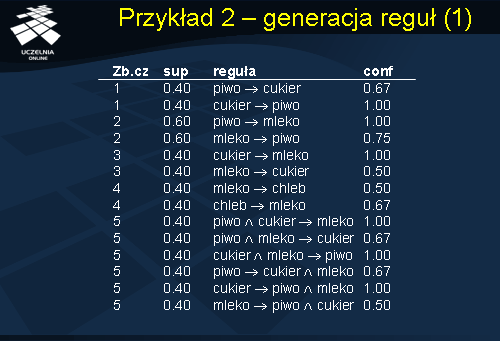
Ostatnią fazą algorytmu jest sprawdzenie, które z wygenerowanych reguł spełniają warunek minimalnej ufności minconf. Reguły, których ufność jest mniejsza od minconf są odrzucane. W naszym przykładzie minimalny próg ufności reguły minconf = 70%. W ten sposób otrzymano zbiór reguł, które zostały umieszczone na powyższym slajdzie.




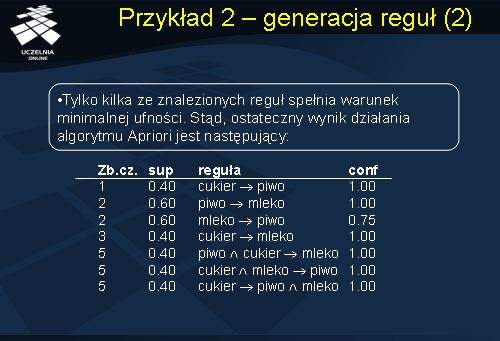
Po weryfikacji współczynnika ufności dla otrzymanych reguł uzyskaliśmy ostateczny zbiór binarnych reguł asocjacyjnych. Tylko kilka ze znalezionych reguł spełnia warunek minimalnej ufności – stąd w wyniku końcowym pozostało 7 reguł.


Idea algorytmu - FP Growth



Diametralnie inne podejście do problemu odkrywania zbiorów częstych zaproponowano w algorytmie FP-Growth. W algorytmie tym

proces odkrywania zbiorów częstych jest realizowany w dwóch krokach:




Kompresja bazy danych



Pierwszy krok algorytmu rozpoczyna się od odczytu bazy danych D w celu znalezienia wszystkich 1-elementowych zbiorów częstych (analogicznie jak w przypadku algorytmu Apriori). Następnie, z każdej transakcji Ti należących do bazy danych D, i=1,..., n, są usuwane te elementy, które nie są częste, to jest, nie są 1-elementowymi zbiorami częstymi. W wyniku otrzymujemy zmodyfikowany zbiór transakcji T = T1,T2,..., Tn, zawierających wyłącznie elementy będące 1-elementowymi zbiorami częstymi. (Otrzymana w wyniku tej transformacji baza danych D ma, najczęściej, znacznie mniejszy rozmiar aniżeli wyjściowa baza danych D. Stąd nazwa kroku – krok kompresji bazy danych).


Dla każdej transakcji {Ti}, i = 1, 2, ..., n, elementy transakcji są, następnie, sortowane według malejących wartości ich wsparcia, tworząc listę elementów. Posortowane transakcje T1, T2,...,Tn, w ostatnim etapie tego kroku, są transformowane do FP-drzewa.



FP -drzewo



FP- drzewo jest ukorzenionym, etykietowanym w wierzchołkach, grafem acyklicznym. Korzeń grafu posiada etykietę 'null', pozostałe wierzchołki grafu, zarówno wierzchołki wewnętrzne jak i liście, reprezentują 1-elementowe zbiory częste. Z każdym wierzchołkiem grafu, za wyjątkiem korzenia, związana jest etykieta reprezentująca 1-elementowy zbiór częsty oraz licznik transakcji, reprezentujący liczbę transakcji wspierających dany zbiór.


Transformacja do FP-drzewa



Transformacja skompresowanej bazy danych D do FP- drzewa jest realizowana w następujący sposób. Tworzymy korzeń FP- drzewa i przypisujemy mu etykietę 'null'. Następnie, dokonujemy ponownego odczytu bazy danych D i dla pierwszej transakcji T1 należącej do D, tworzymy ścieżkę w FP-drzewie, której początkiem jest korzeń drzewa. Kolejność występowania elementów w posortowanej transakcji odpowiada kolejności wierzchołków w ścieżce reprezentującej daną transakcję. Dla każdego wierzchołka należącego do ścieżki, wartość licznika transakcji jest, początkowo, równa 1.





Dla kolejnej transakcji T2 należącej do D tworzymy następną ścieżkę rozpoczynającą się od korzenia. Jeżeli lista elementów transakcji T2 posiada wspólny prefiks z listą elementów transakcji T1, wówczas, ścieżka reprezentująca T2 jest konstruowana w następujący sposób. Załóżmy, że wspólny prefiks transakcji Tr1 i Tr2 składa się z elementów: I1, I2, ..., Ik, gdzie Ii ? T1, Ii ? T2, i = 1, ..., k.




Transformacja elementów transakcji Tr2 należących do wspólnego prefiksu I1, I2, ..., Ik nie tworzy nowych wierzchołków drzewa, lecz współdzieli istniejącą w FP-drzewie ścieżkę I1, I2, ..., Ik utworzoną przy transformacji transakcji Tr1. Pozostałe elementy transakcji Tr2, nie należące do wspólnego prefiksu, tworzą nowe wierzchołki połączone łukami - początkiem tej ścieżki jest wierzchołek Ik.




Transformacja elementów transakcji T2 należących do wspólnego prefiksu I1, I2, ..., Ik nie tworzy nowych wierzchołków drzewa, lecz współdzieli istniejącą w FP- drzewie ścieżkę I1, I2,..., Ik utworzoną przy transformacji transakcji T1. Pozostałe elementy transakcji T2, nie należące do wspólnego prefiksu, tworzą nowe wierzchołki połączone łukami. Początkiem tej ścieżki jest wierzchołek Ik. Ogólnie, w przypadku transformacji transakcji Tj, która posiada wspólny prefiks z przetransformowaną wcześniej transakcją Ti, transakcja Tj, po transformacji, współdzieli podścieżkę reprezentującą wspólny prefiks z transakcją Ti. Innymi słowy, pojedyncza ścieżka w FP- drzewie, rozpoczynająca


się w korzeniu drzewa, reprezentuje zbiór transakcji zawierających identyczne elementy. Licznik ostatniego wierzchołka danej ścieżki zawiera informację o liczbie transakcji wspierających zbiór elementów reprezentowanych przez wierzchołki grafu należące do tej ścieżki.





W celu przyspieszenia i ułatwienia przeszukiwania FP- drzewa, algorytm FP- Growth utrzymuje dodatkową strukturę pełniącą rolę katalogu, nazywaną tablicą nagłówków elementów, lub krótko tablicą nagłówkową, która dla każdego elementu wskazuje na jego lokalizację w FP- drzewie. Jeżeli dany element występuje wielokrotnie w FP- drzewie, to wskaźniki do wierzchołków reprezentujących dany element tworzą listę wskaźników.


Przykład FP-drzewa



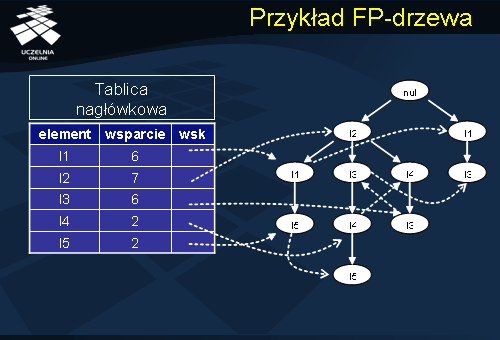
Powyższy slajd przedstawia FP-drzewo z odpowiednią tablicą nagłówkową zawierającą listę wskaźników do poszczególnych elementów w drzewie.


Eksploracja FP-drzewa



W kroku drugim algorytmu, FP- drzewo jest eksplorowane w celu znalezienia wszystkich zbiorów częstych. Proces eksploracji FP-drzewa bazuje na obserwacji, że dla każdego 1-elementowego zbioru częstego alpha, wszystkie częste nadzbiory zbioru alpha są reprezentowane w FP-drzewie przez ścieżki zawierające wierzchołek (wierzchołki) alpha. Eksploracja FP- drzewa jest realizowana w następujący sposób.




Dla każdego 1-elementowego zbioru częstego alpha znajdujemy wszystkie ścieżki w FP- drzewie, których końcowym wierzchołkiem

jest wierzchołek reprezentujący zbiór alpha. Pojedynczą ścieżkę, której końcowym wierzchołkiem jest alpha, nazywać będziemy ścieżką prefiksową wzorca alpha (ang. prefix path). Z każdą prefiksową ścieżką wzorca alpha jest związany licznik częstości ścieżki, którego wartość odpowiada wartości licznika transakcji wierzchołka końcowego ścieżki reprezentującego zbiór alpha.





Zbiór wszystkich ścieżek prefiksowych wzorca tworzy warunkową bazę wzorca (ang. conditional pattern base). Warunkowa baza wzorca służy do konstrukcji tak zwanego warunkowego FP-drzewa wzorca alpha, oznaczanego Tree_alpha. Warunkowe FP-drzewo jest, następnie, rekursywnie eksplorowane w celu znalezienia wszystkich zbiorów częstych zawierających zbiór alpha.


Procedura FP-Growth



Formalny opis procedury FP- Growth, która w oparciu o FP- drzewo znajduje wszystkie zbiory częste. Parametry początkowe procedury FP- Growth, w momencie inicjacji procedury, są następujące: Tree = FP-drzewo i alpha = null.




Procedura FP-Growth ma następującą postać: (parametrami wejściowymi procedury jak powiedzieliśmy w momencie inicjacji są FP-drzewo i null). Jeżeli FP-drzewo zawiera tylko pojedynczą ścieżkę p, wówczas dla każdej kombinacji beta, wierzchołków ścieżki p generujemy zbiór beta+alpha o wsparciu równym minimalnemu wsparciu elementów należących do zbioru beta. Jeżeli FP-drzewo zawiera więcej niż jedną ścieżkę to dla każdego elementu alpha_i należącego do tablicy nagłówków elementów Tree, generujemy zbiór beta = alpha_i+alpha o wsparciu odpowiadającym wsparciu elementów alpa_i. Tworzymy warunkową bazę wzorca beta oraz warunkowe FP-drzewo wzorca beta oznaczone Tree-beta. Jeżeli Tree-beta jest niepuste, ponownie uruchamiamy procedurę FP-Growth z parametrami Tree-beta i beta.



Przykład 3



Działanie algorytmu FP- Growth ilustruje powyższy przykład. Rozważmy przykładową bazę danych supermarketu D przedstawioną

na slajdzie. Załóżmy następujące wartości minimalnego wsparcia i minimalnej ufności: minsup = 30% i minconf = 70%. Przykładowa baza danych składa się z pięciu transakcji.





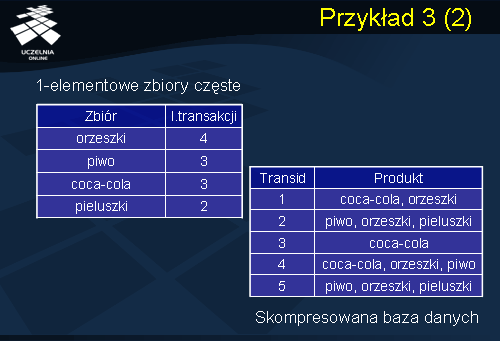
W pierwszym kroku algorytmu znajdujemy wszystkie 1-elementowe zbiory częste. Poniższa tabela przedstawia wszystkie znalezione 1-elementowe zbiory częste wraz z liczbą transakcji wspierających. Dla ilustracji konstrukcji FP- drzewa wartość wsparcia zbioru częstego została zastąpiona w poniższej tabeli wartością licznika transakcji wspierających dany zbiór częsty.

Następnie, z każdej transakcji Ti należącej do D, i=1, ..., n, usuwamy elementy, które nie są 1-elementowymi zbiorami częstymi, i sortujemy pozostałe elementy wewnątrz każdej transakcji według malejących wartości ich wsparcia. W wyniku tej transformacji otrzymujemy następującą skompresowaną bazę danych D.





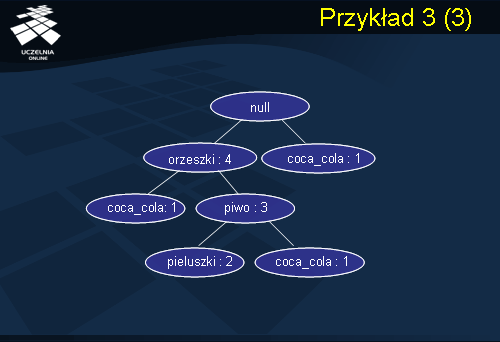
Kolejnym krokiem algorytmu jest transformacja bazy danych D do FP- drzewa. Konstrukcja FP- drzewa rozpoczyna się od utworzenia korzenia drzewa i przypisania mu etykiety null. Odczyt pierwszej transakcji {T_1} z bazy danych D prowadzi do utworzenia ścieżki drzewa: (orzeszki:1) (coca_cola:1) Liczba całkowita występująca po znaku : określa aktualną wartość licznika, związanego z każdym wierzchołkiem, reprezentującego liczbę transakcji wspierających dany element (zbiór częsty 1-elementowy). Transformacja transakcji T2 jest realizowana następująco. Transakcja {T_2} posiada wspólny prefiks (orzeszki) z transakcją T1, stąd, zwiększamy wartość licznika transakcji pierwszego wierzchołka o 1, i tworzymy nową ścieżkę od wierzchołka (orzeszki) zawierającą dwa nowe wierzchołki: (piwo:1) (pieluszki:1). Dla transakcji T3 tworzymy nowy wierzchołek (coca_cola:1), który łączymy z korzeniem drzewa - transakcja T3 nie posiada wspólnego prefiksu z przetransformowanymi transakcjami T1 i T2. Kolejna transakcja T4 posiada wspólny prefiks (orzeszki, piwo) z transakcją T2. Stąd, zwiększamy wartość licznika transakcji każdego z wierzchołków należących do ścieżki reprezentującej wspólny prefiks o 1, (orzeszki:3) (piwo:2), i tworzymy nowy wierzchołek (coca_cola:1), który łączymy łukiem z wierzchołkiem (piwo:2). Ostatnia transakcja {T_5} jest transformowana do istniejącej już ścieżki (orzeszki:3) (piwo:2) (pieluszki:1), stąd, zwiększamy wartość licznika transakcji każdego z wierzchołków należących do tej ścieżki o 1. Ostatecznie, w wyniku transformacji bazy danych D, otrzymujemy FP- drzewo przedstawione na powyższym slajdzie.




Po utworzeniu FP- drzewa, przechodzimy do drugiego kroku algorytmu - eksploracji FP- drzewa zgodnie z procedurą FP- Growth.

Rozpocznijmy od analizy ostatniego znalezionego 1-elementowego zbioru częstego, w porządku malejących wartości wsparcia, to jest, 1-elementowego zbioru pieluszki. Istnieje tylko jedna ścieżka, której wierzchołkiem końcowym jest wierzchołek pieluszki. Stąd, jedyną ścieżką prefiksową wzorca pieluszki jest ścieżka {(orzeszki, piwo) : 2}. Licznik częstości tej ścieżki przyjmuje wartość licznika transakcji wierzchołka pieluszki i jest równa 2 (wartość ta jest podana po znaku :).





Ścieżka {(orzeszki, piwo) : 2} tworzy warunkową bazę wzorca pieluszki. Warunkowe FP- drzewo, związane ze wzorcem pieluszki, zawiera tylko jedną ścieżkę {(orzeszki: 2, piwo: 2)} Zgodnie z procedurą FP- Growth ścieżka ta generuje następujące zbiory częste: {(orzeszki, piwo,pieluszki: 2), (orzeszki, pieluszki: 2) oraz (piwo, pieluszki: 2). Wsparcie wygenerowanych zbiorów częstych wynosi 0.4.





Przechodzimy do analizy kolejnego 1-elementowego zbioru częstego coca_cola. Warunkowa baza wzorca coca_cola zawiera 2 ścieżki prefiksowe: {(orzeszki, piwo: 1 )} i {(orzeszki : 1 )}. Warunkowe FP- drzewo, związane ze wzorcem coca_cola, zawiera tylko jeden wierzchołek {(orzeszki: 2)} i generuje tylko jeden zbiór częsty (orzeszki, coca_cola: 2) o wsparciu 40%.




Dla kolejnego 1-elementowego zbioru częstego piwo, warunkowa baza danych zawiera tylko jedną ścieżkę prefiksową:


(orzeszki, : 3 ). Stąd, warunkowe FP- drzewo, związane ze wzorcem piwo, zawiera tylko jeden wierzchołek (orzeszki: 3) i generuje


tylko jeden zbiór częsty (orzeszki, piwo, : 3) o wsparciu 60%. Dla ostatniego 1-elementowego zbioru częstego orzeszki, warunkowa baza wzorca orzeszki jest zbiorem pustym, gdyż FP- drzewo nie zawiera żadnych ścieżek prefiksowych dla wzorca orzeszki.





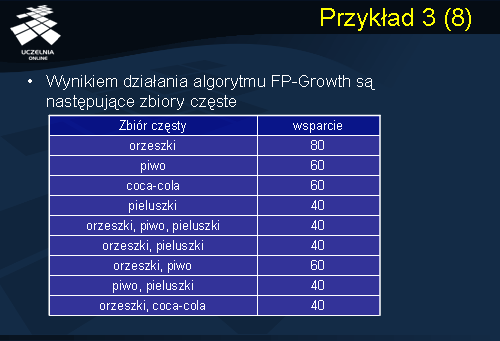
W wyniku działania algorytmu FP- Growth otrzymaliśmy następujące zbiory częste, które podsumowaliśmy w powyższej tablicy.