W4_Wielopoziomowe_i_wielowymiarowe_reguły

Wielopoziomową (lub uogólnioną) regułą asocjacyjną (ang. multilevel association rule, generalized association rule) WRA nazywamy implikację postaci X -> Y, gdzie X zawiera się w I, X i Y są rozłączne i żaden element y należący do Y nie jest poprzednikiem żadnego elementu x należącego do X. Zbiór X nazywamy poprzednikiem reguły, natomiast zbiór Y następnikiem reguły. Czasami, w literaturze, terminem „wielopoziomowa reguła asocjacyjna” określa się regułę asocjacyjną, której poprzednik i/lub następnik zawiera nazwaną grupę elementów taksonomii. W takim przypadku, reguły opisujące asocjacje pomiędzy elementami reprezentowanymi przez liście taksonomii nie są, w myśl tej definicji, wielopoziomowymi regułami asocjacyjnymi. Definicje wsparcia i ufności reguły wielopoziomowej będą identyczne jak w przypadku binarnych jednopoziomowych reguł asocjacyjnych, czyli wielopoziomowa reguła asocjacyjna X -> Y posiada wsparcie s w bazie danych D, 0 <= s <= 1 , jeżeli s% transakcji w D wspiera X U Y. Mówimy, że wielopoziomowa reguła asocjacyjna X -> Y posiada ufność c w bazie danych D, 0 <= s <= 1 , jeżeli c% transakcji w D, które wspierają X, wspierają również Y.

Sformułowanie problemu

Problem odkrywania wielopoziomowych reguł asocjacyjnych można zdefiniować następująco: dana jest baza danych transakcji T oraz taksonomia elementów H - należy znaleźć wszystkie wielopoziomowe reguły asocjacyjne, których wsparcie s jest większe lub równe pewnej minimalnej wartości wsparcia minsup, i których ufność c jest większa lub równa pewnej minimalnej wartości ufności minconf. Powyższe zdefiniowanie problemu odkrywania wielopoziomowych reguł asocjacyjnych zakłada, że próg minimalnego wsparcia jest jednakowy dla wszystkich reguł niezależnie od tego, czy reguła opisuje asocjacje występujące na najniższym poziomie abstrakcji, to jest, asocjacje pomiędzy elementami zbioru I, czy też na wyższym poziomie abstrakcji, to jest, pomiędzy nazwanymi grupami elementów.

Podstawowy algorytm odkrywania WRA

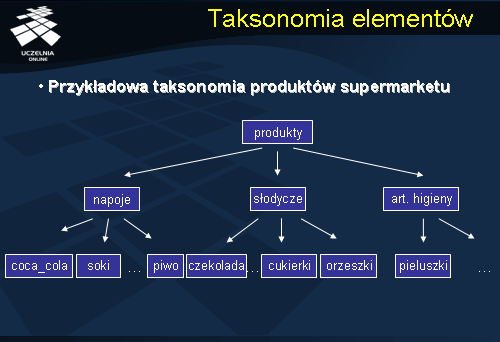
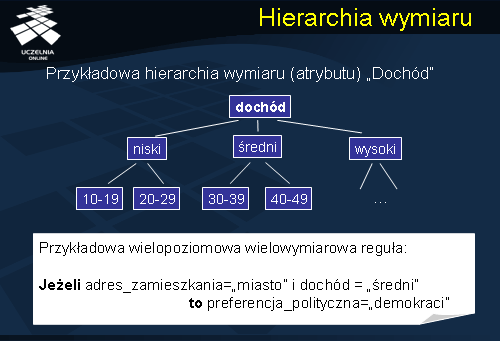
Teraz przejdziemy do omówienia podstawowego algorytmu odkrywania wielopoziomowych reguł asocjacyjnych. Ogólna idea algorytmu odkrywania wielopoziomowych reguł asocjacyjnych, polega na rozszerzeniu każdej transakcji Ti należącej do D, i=1, ..., n o zbiór poprzedników (nazwane grupy elementów) wszystkich elementów należących do transakcji. Pomijamy przy tym rozszerzeniu korzeń taksonomii i, ewentualnie, usuwamy z transakcji powtarzające się elementy. Następnie, w odniesieniu do tak rozszerzonej bazy danych można zastosować dowolny algorytm odkrywania jednopoziomowych reguł asocjacyjnych (np. Apriori). W kroku trzecim algorytmu usuwamy wszystkie trywialne wielopoziomowe reguły asocjacyjne.

Ze zbioru wygenerowanych reguł należy usunąć trywialne wielopoziomowe reguły asocjacyjne. Trywialną regułą asocjacyjną nazywamy regułę postaci wierzchołek -> poprzednik(wierzchołka), gdzie wierzchołek reprezentuje pojedynczy element lub nazwaną grupę elementów. Do usuwania trywialnych wielopoziomowych reguł asocjacyjnych wykorzystujemy taksonomie elementów, po czym usuwamy specjalizowane wielopoziomowe reguły asocjacyjne jedną regułą uogólnioną np.: ‘bułki -> napoje’ oraz ‘rogale -> napoje’ zastąp regułą ‘pieczywo -> napoje’.

Wady podstawowego algorytmu odkrywania WRA

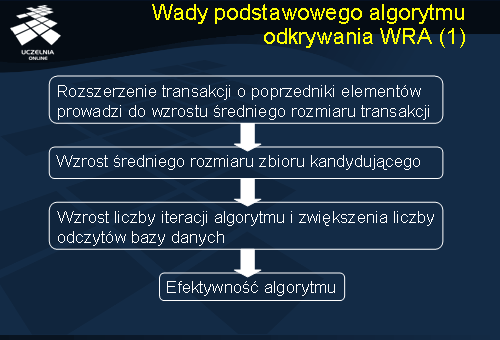
Przedstawiony podstawowy algorytm odkrywania wielopoziomowych reguł asocjacyjnych posiada szereg wad, które w istotny sposób wpływają na jego efektywność. Idea rozszerzenia transakcji o poprzedniki wszystkich elementów należących do transakcji prowadzi w oczywisty sposób do zwiększenia średniego rozmiaru transakcji, co z kolei prowadzi do zwiększenia średniego rozmiaru zbioru kandydującego. Wzrost średniego rozmiaru zbioru kandydującego prowadzi do zwiększenia liczby iteracji algorytmu, a co za tym idzie, do zwiększenia liczby odczytów bazy danych w fazie obliczania wsparcia zbiorów kandydujących, co istotnie pogarsza efektywność algorytmu. Wzrost średniego rozmiaru zbioru kandydującego prowadzi również do znacznego zwiększenia liczby zbiorów kandydujących, co w konsekwencji również istotnie pogarsza efektywność algorytmu.

W literaturze zaproponowano szereg wariantów podstawowego algorytm odkrywania wielopoziomowych reguł asocjacyjnych: Cumulate, Stratify, Estimate, oraz EstMerge, których celem jest poprawa efektywności fazy znajdowania zbiorów częstych.

Przedstawione podejście do odkrywania wielopoziomowych reguł asocjacyjnych nastręcza jeszcze jeden istotny problem. Zauważmy, że przedstawione w powyższym algorytmie odkrywania wielopoziomowych reguł asocjacyjnych podejście zakłada jednakowy próg minimalnego wsparcia dla wszystkich poziomów abstrakcji taksonomii elementów. Identyczny próg minimalnego wsparcia odnosi się do nazwanej grupy elementów "napoje"' jak i pojedynczego elementu "orzeszki ziemne firmy Felix w opakowaniu 50-gramowym"'. Ma to swoje istotne zalety. Po pierwsze, użytkownik podaje tylko jedną wartość minimalnego wsparcia i minimalnej ufności. Po drugie, upraszcza i optymalizuje procedurę znajdowania zbiorów częstych. Zauważmy bowiem, że dowolny wierzchołek wewnętrzny taksonomii jest nadzbiorem swoich następników - w fazie znajdowania zbiorów częstych można pominąć analizę zbiorów zawierających elementy, których poprzedniki w taksonomii elementów nie są zbiorami częstymi (algorytm Stratify).

Wymienione wyżej wady podejścia zakładającego jednakowy próg minimalnego wsparcia dla wszystkich poziomów taksonomii elementów stanowiły motywację opracowania podejścia, którego podstawowym założeniem jest zmniejszanie wartości minimalnego wsparcia dla kolejnych, idąc od korzenia, poziomów taksonomii. Algorytmy odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia Multi_AssocRedSup. Punktem wyjścia przy konstrukcji algorytmów odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia jest założenie, że dla każdego poziomu taksonomii elementów definiujemy niezależny próg minimalnego wsparcia. Im niższy poziom taksonomii, tym mniejszy próg minimalnego wsparcia.

Zmienny próg minimalnego wsparcia

Punktem wyjścia przy konstrukcji algorytmów odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia jest założenie, że dla każdego poziomu taksonomii elementów definiujemy niezależny próg minimalnego wsparcia. Im niższy poziom taksonomii, tym mniejszy próg minimalnego wsparcia. Wymienione wyżej wady podejścia zakładającego jednakowy próg minimalnego wsparcia dla wszystkich poziomów taksonomii elementów stanowiły motywację opracowania podejścia, którego podstawowym założeniem jest zmniejszanie wartości minimalnego wsparcia dla kolejnych, idąc od korzenia, poziomów taksonomii. Algorytmy odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia Multi_AssocRedSup. Punktem wyjścia przy konstrukcji algorytmów odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia jest założenie, że dla każdego poziomu taksonomii elementów definiujemy niezależny próg minimalnego wsparcia. Im niższy poziom taksonomii, tym mniejszy próg minimalnego wsparcia. Próg minimalnego wsparcia dla poziomu i wynosi minsup = 0.2, natomiast dla poziomu i+1 wynosi 0.1. Wsparcie zbiorów "coca_cola"' oraz "piwo"' wynosi 0.11, zatem, oba zbiory są częste. Wsparcie zbioru "napoje"' wynosi 0.22 i jest większe niż minsup dla poziomu i. Zatem, zbiór "napoje"' jest również zbiorem częstym. Gdyby przyjąć jednakowy próg minimalnego wsparcia, na przykład minsup = 0.2, wówczas tylko zbiór "napoje" byłby zbiorem częstym.

Ogólny algorytm odkrywania WRA o zmiennym progu minsup

Ogólny algorytm odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia jest algorytmem schodzącym (ang. top-down algorithm). W pierwszym kroku jest obliczane wsparcie elementów występujących na najwyższym poziomie taksonomii (pomijamy korzeń taksonomii). Elementy, których wsparcie jest większe od zadanego progu minimalnego wsparcia dla danego poziomu są dodawane do listy zbiorów częstych. W kolejnych krokach jest obliczane wsparcie dla elementów występujących na kolejnych, niższych poziomach taksonomii, aż nie zostanie osiągnięty poziom liści taksonomii. Do znajdowania zbiorów częstych na danym poziomie taksonomii można zastosować dowolny algorytm odkrywania zbiorów częstych.

Generowanie zbiorów częstych

Istnieje szereg wariantów nakreślonego powyżej ogólnego algorytmu odkrywania wielopoziomowych reguł asocjacyjnych o zmiennym progu minimalnego wsparcia. Warianty te różnią się przyjętą strategią przeszukiwania przestrzeni zbiorów kandydujących:

Strategia niezależnych poziomów jest strategią wyczerpującą, która zakłada, że poziomy taksonomii są wzajemnie niezależne. Oznacza to, że w fazie generowania zbiorów kandydujących każdy wierzchołek taksonomii jest analizowany niezależnie od swoich poprzedników lub następników. Innymi słowy, wszystkie wierzchołki taksonomii reprezentują ten sam poziom abstrakcji, to jest, reprezentują niezależne elementy (podobnie jak w przypadku odkrywania binarnych reguł asocjacyjnych). W konsekwencji, strategia niezależnych poziomów analizuje wsparcie każdego zbioru kandydującego niezależnie od tego, czy jego poprzednik w taksonomii elementów jest zbiorem częstym czy też nie. Niestety, prowadzi to do analizy wielu zbiorów kandydujących, które z definicji nie są zbiorami częstymi.

Strategia krzyżowej filtracji zbioru k-elementowego zakłada, że analizie poddawane są tylko te zbiory kandydujące, których elementy są następnikami zbiorów częstych k-elementowych. Przykładowo, jeżeli zbiór „piwo, pieczywo” jest zbiorem częstym, to zbiorami kandydującymi poddawanymi analizie są, na przykład, zbiory „piwo_żywiec, bułki_kajzerki” lub „piwo_lech, rogale”. Ta strategia, z kolei, prowadzi do automatycznego odrzucenia wielu interesujących częstych zbiorów kandydujących, takich, dla których poprzedniki elementów należących do tych zbiorów nie są częste. Przykładowo, załóżmy, że wsparcie nazwanej grupy elementów „piwo_żywiec”, występującej na i-tym poziomie taksonomii, jest większe od prógu minimalnego wsparcia zdefiniowanego dla tego poziomu taksonomii, natomiast wsparcie nazwanej grupy elementów "piwo"', występującej na i-1-tym poziomie taksonomii, jest mniejsze aniżeli próg minimalnego wsparcia dla poziomu i-1 taksonomii. Strategia krzyżowej filtracji zbioru k-elementowego automatycznie odrzuci zbiór częsty „piwo_żywiec, art. higieny”, który może być zbiorem częstym.

Strategia krzyżowej filtracji pojedynczego elementu jest próbą kompromisu pomiędzy wspomnianymi wcześniej strategiami przeszukiwania przestrzeni zbiorów kandydujących. Zbiór kandydujący jest analizowany na i-tym poziomie jeżeli jego poprzednik na poziomie i-1 jest zbiorem częstym. Innymi słowy, jeżeli zbiór x na poziomie i jest częsty, to analizie są poddawane jego następniki. Przykładowo, jeżeli zbiór „piwo” nie jest częsty, to w dalszej analizie pomija się zbiory „piwo_żywiec" oraz „piwo_lech”. Strategia ta posiada jednak podobną wadę jak strategia krzyżowej filtracji zbioru k-elementowego, to jest, może ona prowadzić do automatycznego odrzucenia interesujących częstych zbiorów kandydujących, takich, dla których poprzedniki elementów należących do tych zbiorów nie są częste. Próbą rozwiąania tego problemu było zaproponowanie zmodyfikowanej wersji strategii krzyżowej filtracji pojedynczego elementu, nazwanej kontrolowaną strategią krzyżowej filtracji pojedynczego elementu (ang. controlled level-cross filtering strategy by single item).

Wielowymiarowe reguły asocjacyjne

Pozostała nam jeszcze jedna klasa reguł asocjacyjnych, rozpatrywanych w kontekście wymiarowości przetwarzanych danych. Aby przybliżyć pojęcie analizy wielowymiarowej, rozważmy, dla przykładu, problem analizy i generowania raportów opisujących sprzedaż wina w sieci supermarketów. Załóżmy, że sprzedaż wina jest mierzona ilością butelek sprzedanych w określonym przedziale czasu. Miarą analizy jest zatem ilość sprzedanych butelek wina. Wartość tej miary jest, najczęściej, funkcją następujących „wymiarów” analizy: czasu, rodzaju wina oraz oddziału supermarketu. Może się zatem zdarzyć, że różne wymiary analizy będą posiadały tą samą dziedzinę wartości. Na przykład, dla wymiarów „adres supermarketu” i „adres klienta”, dziedziną wartości będzie zbiór adresów reprezentowanych przez łańcuchy znaków. Reguła może być zatem wielowymiarowa nawet, jeżeli dane występujące w regule reprezentują tę samą dziedzinę wartości.

Wielowymiarową regułą asocjacyjną nazywamy regułę, w której dane w niej występujące reprezentują różne dziedziny wartości. Atrybuty (wymiary) mogą być dwojakiego rodzaju ciągłe (ilościowe) lub kategoryczne (nominalne). Reguły wielowymiarowe określają współwystępowanie wartości danych ciągłych i/lub kategorycznych.

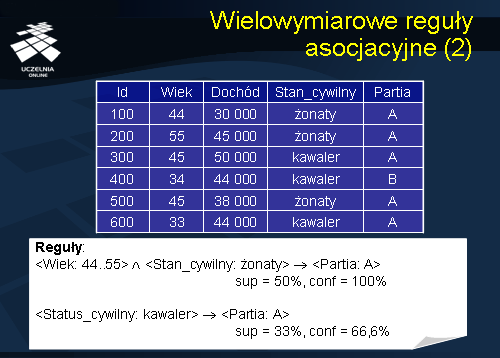
Dla zilustrowania wielowymiarowych reguł asocjacyjnych rozważmy przykład umieszczony na slajdzie. Dana jest baza danych sondażowych przedstawiających wyniki głosowania określonych osób, o określonych parametrach i określonej partii politycznej. Przykładowo osoba o identyfikatorze 100, lat 44, dochodzie 30 000, stan cywilny żonaty – głosował na partię A. W prezentowanej bazie danych można przedstawić następujące otrzymane reguły wielowymiarowe postaci:

<Wiek: 44..55> i <Stan_cywilny: żonaty> -> <Partia: A> sup = 50%, conf = 100%

<Status_cywilny: kawaler> -> <Partia: A>sup = 33%, conf = 66,6%

Problemy

Z wielowymiarowymi regułami asocjacyjnymi wiąże się szereg problemów. Po pierwsze dane ciągłe (np. atrybut „zarobek” w analizowanym przez nas przykładzie) może być bardzo różnorodny. Gdybyśmy brali pod uwagę wszystkie możliwe wartości jakie może przyjąć ten atrybut, znalezienie jakichkolwiek zależności między atrybutami byłoby bardzo ograniczone, lub wręcz niemożliwe. Dane ciągłe wymagają odpowiedniego przygotowania zwanego dyskretyzacją. Szerzej na temat dyskretyzacji powiemy w dalszej części wykładu.

Drugim problemem są brakujące dane w bazie danych czyli wartości puste (null values), w tym wypadku przyjmujemy dwie strategie. Albo pomijamy rekordy zawierające brakujące dane, albo próbujemy uzupełnić brakujące dane.

Jeżeli decydujemy się na uzupełnienie danych musimy przyjąć założenie o świecie otwartym lub zamkniętym. W przypadku założenia o świecie otwartym zakładamy, że dane mogą przyjąć dowolne wartości. W drugim przypadku, zakładamy że wartości jakie przyjmuje atrybut są atrybutami występującymi w bazie danych. W takim przypadku możemy wykorzystać algorytm znajdowania zależności funkcyjnych w bazie danych. Korzystając z wiedzy z odkrytych zależności funkcyjnych możemy uzupełnić brakujące dane.

Transformacja problemu

Problem odkrywania reguł wielowymiarowych jest problemem trudnym. Do każdego nowego problemu możemy podejścia w dwojaki sposób. Podejście pierwsze polegałoby na opracowaniu nowych specyficznych algorytmów rozwiązywania tego problemu. Podejście drugie, nazwane przez nas klasycznym podejściem rozwiązania problemów jest transformacja problemu odkrywania wielowymiarowych reguł asocjacyjnych do problemu znajdowania binarnych reguł asocjacyjnych. W pierwszym kroku dokonujemy dyskretyzacji atrybutów ciągłych, czyli dzielimy zbiór możliwych wartości przyjmowanych przez atrybut, na przedziały wartości. Przykładowo, atrybut „wiek” możemy podzielić na przedziały odpowiednio [20, 29], [30,39], itd. Innym rozwiązaniem jest tworzenie rekordów postaci boolowskiej. W tym wypadku atrybuty kategoryczne traktujemy w ten sposób, że każda wartość atrybutu kategorycznego stanowi osobny „produkt”. Natomiast, w przypadku atrybutów ciągłych każdy przedział atrybutu stanowi osobny „produkt”.

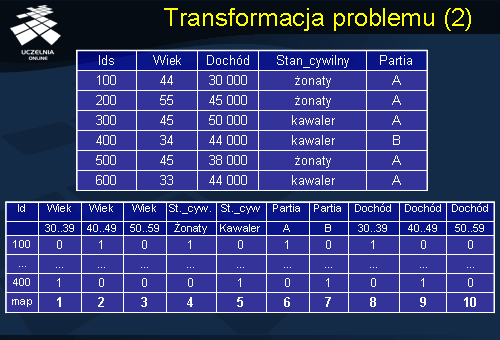
Rozważmy przykład ilustrujący transformację problemu odkrywania wielowymiarowych reguł asocjacyjnych do problemu odkrywania binarnych reguł asocjacyjnych. Dana jest relacja przedstawiona na slajdzie opisująca wyniki głosowania określonych osób na określone partie. Proces transformacji rozpoczyna się od procesu dyskretyzacji atrybutów ciągłych. W naszym przypadku będzie to atrybut wiek oraz atrybut dochód. Wcześniej wspomniany atrybut wiek poddajemy dyskretyzacji, czyli dzielimy na przedziały [30..39],[40..49],[50..59]. Podobnie dyskretyzujemy atrybut ciągły dochód dzielimy na trzy przedziały wartości [30..39],[40..49],[50..59]. Następnie transformujemy oryginalną relacje do postaci rekordów w postaci boolowskiej. Transformacja polega na utworzeniu osobnego atrybutu dla każdego przedziału wartości dla atrybutu ciągłego oraz utworzeniu osobnego atrybutu dla każdej wartości atrybutu kategorycznego. Stąd w naszej nowej relacji, która będzie zawierała rekordy w postaci boolowskiej, otrzymujemy następujące atrybuty: trzy atrybuty odpowiadające trzem przedziałom wartości atrybutu wiek; następnie dwa atrybuty odpowiadające wartościom atrybutu kategorycznego stan cywilny; następnie dwa atrybuty odpowiadające wartościom atrybutu kategorycznego partia, wreszcie trzy atrybuty odpowiadające trzem przedziałom atrybutu dochód. Dodajemy wiersz „map”, w którym mapujemy kolumny, nadając im poszczególne identyfikatory.

Następnie numerujemy wszystkie atrybuty, w naszym przypadku mamy 10 atrybutów ponumerowanych od 1 do 10. Następnie tworzymy nową tablicę przedstawioną na slajdzie składającą się z dwóch kolumn: kolumna Id oraz kolumna Produkty. Kolumna Id odpowiada identyfikatorom rekordów z oryginalnej relacji, natomiast kolumnę Produkty tworzymy w następujący sposób – wpisujemy dla danego rekordu numery atrybutów dla których dany rekord posiada wartość 1. Po dokonaniu transformacji wszystkich rekordów otrzymujemy następująca tablicę przedstawioną na slajdzie. Otrzymana tablica łudząco przypomina nam znaną tablicę, którą eksplorowaliśmy w celu znalezienia binarnych reguł asocjacyjnych. Możemy zastosować dowolny z algorytmów odkrywania binarnych reguł asocjacyjnych w celu znalezienia wszystkich zbiorów częstych i wszystkich reguł asocjacyjnych. Zakładamy próg minimalnego wsparcia = 30%.

Transformacja problemu - znajdowanie zbiorów częstych

Załóżmy, że zastosujemy algorytm Apriori w celu znalezienia wszystkich zbiorów częstych i reguł asocjacyjnych. Rozpoczynamy od listy wszystkich produktów (C1). Dla każdego produktu obliczamy wsparcie określonego produktu. Dzięki temu znajdujemy wszystkie zbiory częste 1-elementowe zaznaczone na slajdzie L1. Do L1 należą zbiory częste {1,2,4,5,6,8,9}. Następnie w oparciu o L1 obliczamy wszystkie zbiory kandydujące 2-elementowe (C2). Ponownie obliczamy wsparcie dla każdego zbioru kandydującego usuwamy wszystkie zbiory kandydujące, które nie spełniają progu minimalnego wsparcia oraz usuwamy wszystkie te zbiory kandydujące, które zawierają podzbiory, które nie są częste. W konsekwencji otrzymujemy L2 – zbiory częste 2-elementowe przedstawione na slajdzie. W naszym przykładzie wsparcie zbiorów częstych jest dla ułatwienia liczone liczbą transakcji wspierających dany zbiór.

Stosując kolejne iteracje algorytmu Apriori dochodzimy do zbioru zawierającego zbiór częsty 4-elementowy L4={2 4 6 8}. W kolejnym kroku algorytmu Apriori z podanych zbiorów częstych możemy otrzymać reguły asocjacyjne. Przykładowo ze zbioru L4 otrzymamy następujące reguły asocjacyjne: Pierwsza reguła: Jeżeli klient jest w przedziale wiekowym (40..49) i jest żonaty a jego dochód wynosi w granicach (30tys.-39tys) to dana osoba należy do Partii ‘A’. Reguła druga brzmi następująco: Jeżeli dochód klienta wynosi w granicach (30tys.-39tys) i jest żonaty oraz należy do Partii ‘A’ to jego wiek prawdopodobnie należy do przedziału (40-49).

Dyskretyzacja atrybutów ilościowych

Wróćmy obecnie do problemu dyskretyzacji atrybutów ilościowych. Istnieje wiele schematów dyskretyzacji atrybutów ilościowych, jednakże trzy schematy są najbardziej popularne. Dyskretyzując atrybuty ilościowe tworzymy przedziały o równej szerokości. W tym schemacie zakładamy, że rozmiar każdego przedziału jest identyczny (np. przedziały 10tys. dla atrybutu „dochód”). Schemat dyskretyzacji na przedziały o równej gęstości zakłada, że każdy przedział posiada zbliżoną (równą) liczbę rekordów przypisanych do przedziału. Schemat dyskretyzacji poprzez grupowanie (cluster-based) zakłada on, że cały zbiór wartości poddajemy procesowi grupowania, znajdujemy skupienia wartości dyskretyzowanego atrybutu, w oparciu o skupienia tworzymy podział wartości danego atrybutu ilościowego.

Dyskretyzacja może mieć charakter statyczny lub dynamiczny. Dyskretyzacja statyczna to dyskretyzacja, która dzieli zbiór wartości danego atrybutu apriori na przedziały niezależnie od rozkładu wartości danego atrybutu. Pod pojęciem dyskretyzacji dynamicznej rozumiemy taki podział zbioru wartości atrybutów na przedziały, który może być rozpatrywana w oparciu o rozkład wartości atrybutu lub w oparciu o odległości pomiędzy wartościami danego atrybutu.

Wielopoziomowe wielowymiarowe reguły asocjacyjne

Podobnie jak w przypadku binarnych reguł asocjacyjnych tak również w przypadku wielowymiarowych reguł asocjacyjnych możemy być zainteresowani poszukiwaniem wielopoziomowych, wielowymiarowych reguł asocjacyjnych. Dla każdego atrybutu (wymiaru) bazy danych można zdefiniować hierarchię wymiaru (analogicznie do taksonomii elementów w przypadku wielopoziomowych reguł asocjacyjnych). Wielowymiarowe reguły asocjacyjne reprezentujące asocjacje pomiędzy nazwanymi poziomami hierarchii wymiarów atrybutów nazywamy wielopoziomowymi lub uogólnionymi wielowymiarowymi regułami asocjacyjnymi.

Hierarchia wymiaru

Przykładowo dla atrybutu dochód rozważanym wcześniej przez nas w przykładzie możemy zdefiniować następującą hierarchię atrybutu. Możemy założyć, że przedziały wartości [10-19] oraz [20-29] są przedziałami oznaczającymi niski dochód, przedziały [30-39],[40-49] będzie oznaczał dochód średni, natomiast przedział np.. [50-59] będzie oznaczał dochód wysoki. Przykładową wielopoziomową, wielowymiarową regułą asocjacyjną może być reguła następującej postaci: Jeżeli adres_zamieszkania = „miasto” i dochód = „średni” to preferencja_polityczna = „demokraci”.

Problem oceny reguł asocjacyjnych

Na zakończenie wykładu powróćmy do problemu oceny reguł asocjacyjnych. J.Han w swoim fundamentalnym podręczniku dotyczącym eksploracji danych sformułował następujące pytanie: [W jaki sposób system eksploracji danych, odkrywając reguły asocjacyjne, może określić, które ze znalezionych reguł są interesujące dla użytkownika?]. Otóż okazuje się, że reguły o dużym wsparciu niekoniecznie muszą okazać się interesujące. Co więcej okazuje się, że reguły te są z reguły dobrze znane użytkownikom. Podobnie rzecz ma się w odniesieniu do reguł o wysokim współczynniku ufności, czyli reguł pewnych najczęściej również dobrze znanych użytkownikom. Okazuje się, że w ostatecznym rozrachunku przydatność reguły potrafi określić tylko i wyłącznie użytkownik.

Problemy reguł asocjacyjnych

Ostatnie stwierdzenie, że tylko użytkownik (specjalista dziedzinowy) potrafi racjonalnie ocenić, na ile znaleziona reguła asocjacyjna jest interesująca jest stwierdzeniem pesymistycznym, ponieważ mówi ono, że nie istnieją obiektywne miary na ocenę czy dana reguła jest interesująca dla użytkownika czy też nie. Weźmy przykład, reguły znalezionej w szpitalnej bazie danych: „przetoczenie ponad 2,5 jednostek krwi prowadzi często do komplikacji pooperacyjnych”. Czy otrzymana reguła jest interesująca? Informacja taka jest powszechnie dostępna, można ją znaleźć w każdym podręczniku chirurgii. Jak zauważyliśmy wcześniej miary wsparcia i ufności nie pozwalają na odpowiedź, czy dana reguła asocjacyjna jest interesująca czy nie. Pojawia się pytanie „czy można podać ranking reguł z punktu widzenia, na ile uzyskane reguły są interesujące”?.

Przykład

Rozważmy jeszcze jeden przykład, który ilustruje słabości miar wsparcia i ufności. Dana jest tablica na powyższym slajdzie, przedstawiającą wyniki ankiety dotyczącej preferencji klientów w zakresie herbaty i kawy. Ankietowanych było 100 osób, 90 osób deklaruje się jako osoby, które piją kawę, z których 20 osób pije również herbatę. 70 osób lubi kawę, ale nie lubi herbaty. Pozostałe 10 osób nie lubi kawy, a ich preferencje rozkładają się następująco: 5 osób nie lubi kawy, ale lubi herbatę, natomiast pozostałe 5 osób nie lubi ani kawy, ani herbaty. Reasumując z przedstawionej tabeli wynikają następujące wnioski: Spośród 100 ankietowanych 90 deklarowało się jako zwolennicy kawy, 10 deklarowało się jako osoby, które nie lubią kawy, 25 osób deklarowało, że lubi herbatę i 75 osób deklarowało, że nie lubi herbaty. W dostarczonych zestawie danych znaleziono następującą regułę asocjacyjną: Ci którzy lubią herbatę lubią również kawę, reguła posiada wsparcie wynosi 20/100 =20% oraz ufność 20/25=80%.

Z podanej reguły możemy wnioskować: „Kto lubi herbatę, najczęściej, lubi również kawę”. Otrzymana reguła ma duże wsparcie oraz wysoką ufność. Jednak analizując przedstawioną na poprzednim slajdzie tabelę, dochodzimy do następującej konkluzji: przedstawiona reguła posiada wsparcie 20%, jest to o tyle zaskakujące, że aż 90% ankietowanych deklaruje się jako zwolennicy kawy. Skąd różnica wartości wsparcia reguły na poziomie 20% i deklarowanej preferencji do kawy 90% ankietowanych. Jeżeli przyjrzymy się tabeli ponownie, dojdziemy do wniosku, że ludzie, którzy lubią herbatę najczęściej nie lubią kawy. Istnieje negatywna korelacja pomiędzy preferencją „lubię herbatę” i „lubię kawę”. Gdybyśmy wygenerowali regułę przeciwną: ‘Ci, którzy nie lubią herbaty, ale lubią kawę” ma wsparcie 70% oraz ufność 93%.

Korelacja

Mimo, że reguła ‘kto lubi herbatę lubi również kawę’ jest regułą o stosunkowo dużym wsparciu i wysokiej ufności, to okazało się na podstawie naszego przykładu, że reguła przeciwna ‘kto nie lubi herbaty ten lubi kawę’ jest regułą o znacznie większym wsparciu i większej ufności. Jakie są praktyczne konsekwencje tego spostrzeżenia? Pierwszy wniosek mówi, że miary wsparcia i ufności nie wystarczają do pełnej oceny ważności reguł asocjacyjnych. Drugi wniosek mówi, że jeżeli wygenerowaliśmy zbiór reguł asocjacyjnych to powinniśmy jeszcze sprawdzić, czy zbiór przeciwnych reguł (nie poprzednik reguły -> następnik reguły) nie posiada przypadkiem większego wsparcia i większej ufności. W literaturze zaproponowano szereg nowych miar oceny ważności reguł asocjacyjnych: lift, conviction, any-confidence, all-confidence, bond, gain, itp., aby móc empirycznie określić przydatność reguły asocjacyjnej. Spośród zaproponowanych nowych miar skoncentrujemy się na mierze Lift (lub Interest), która szeroko stosowana jest przez wiele produktów komercyjnych. Aby wprowadzić definicję tej miary wcześniej przybliżymy definicję korelacji. Mówimy, że dwa zdarzenia A i B są niezależne, jeżeli prawdopodobieństwo wystąpienia tych zdarzeń jest równe iloczynowi prawdopodobieństw wystąpienia tych zdarzeń), w przeciwnym razie zdarzenia A i B są skorelowane.

Korelacja - Lift

Miara Lift jest miarą korelacji pomiędzy poprzednikiem i następnikiem reguły asocjacyjnej. Jeżeli wartość miary Lift wynosi 1 oznacza, że zdarzenia reprezentujące poprzednik reguły i następnik reguły są niezależne. Jeżeli wartość miary Lift < 1 oznacza iż zdarzenia reprezentujące poprzednik i następnik reguły są skorelowane negatywnie, wówczas należałoby rozważać regułę przeciwną. Jeżeli wartość miary Lift > 1 oznacza to, że zdarzenia reprezentujące poprzednik i następnik reguły są skorelowane pozytywnie. Wracając do przykładu ‘kto lubi herbatę lubi również kawę’ wartość miary Lift wynosi 0.89, stąd wiemy, że zdarzenia są skorelowane negatywnie, skąd możemy wnioskować, że prawdopodobnie reguła przeciwna ‘Kto nie lubi herbaty najczęściej lubi kawę”, będzie regułą asocjacyjną o większym wsparciu i większej ufności niż oryginalna rozpatrywana reguła.