Odkrywanie wzorców sekwencji
Na wykładzie zapoznamy się z problemem odkrywania wzorców sekwencji. Rozpoczniemy od wprowadzenia oraz sformułowania problemu. Następnie wprowadzimy szereg nowych definicji, z którymi będziemy się posługiwać w eksploracji wzorców sekwencji. Przedstawimy poszczególne kroki algorytmu GSP oraz zilustrujemy jego działanie na przykładzie.
Eksploracja wzorców sekwencji

Wzorce sekwencji stanowią ważną klasę wzorców symbolicznych opisujących zależności występujące pomiędzy zdarzeniami zachodzącymi w pewnym przedziale czasu. W przypadku wzorców symbolicznych zdarzenia są opisane wartościami atrybutów kategorycznych. W przypadku, gdy zdarzenia są opisane wartościami numerycznymi mówimy o przebiegach czasowych lub o analizie trendów. W przypadku analizy trendów, najczęściej stosuje się metody analizy przebiegów czasowych lub metody predykcji., jest związana etykieta czasowa opisująca czas zajścia danego zdarzenia. Problem odkrywania wzorców sekwencji polega, najogólniej mówiąc, na analizie bazy danych zawierającej informacje o zdarzeniach, które wystąpiły w określonym przedziale czasu, w celu znalezienia zależności pomiędzy występowaniem określonych zdarzeń w czasie. Przykładem wzorca sekwencji, który można znaleźć w bazie danych wypożyczalni filmów video, jest następujący wzorzec zachowania klientów wypożyczalni:
‘Klient, który wypożyczył tydzień temu film pod tytułem Gwiezdne wojny, w ciągu tygodnia wypożyczy film pod tytułem Imperium kontratakuje, a następnie, w ciągu kolejnego tygodnia, wypożyczy film po tytułem Powrót Jedi’. Zauważmy, że zdarzenia wchodzące w skład wzorca sekwencji nie muszą występować bezpośrednio jedno po drugim - mogą być przedzielone wystąpieniem innych zdarzeń. W odniesieniu do przedstawionego powyżej wzorca sekwencji, oznacza to, że klient, pomiędzy wypożyczeniem filmu Imperium kontratakuje a Powrót Jedi, wypożycza zwykle jeszcze inny film, ale podana sekwencja opisuje typowe zachowanie większości klientów wypożyczalni.
Przykładem innego wzorca sekwencji jest wzorzec, który można znaleźć analizując log serwera www. Przykładowo: ‘użytkownik, który odczytał stronę A i B przejdzie w kolejnych krokach prawdopodobnie do strony D, a następnie do strony F’.
Dziedziny zastosowań

Metoda odkrywania wzorców sekwencji znalazła zastosowanie w wielu dziedzinach: analiza koszyka zakupów, telekomunikacja, medycyna, ubezpieczenia i bankowość, serwery WWW, itd. W przypadku analizy koszyka zakupów, metodę odkrywania wzorców sekwencji stosuje się w celu znalezienia typowych wzorców zachowań klientów w czasie. Dotyczy to handlu hurtowego lub półhurtowego, gdy potrafimy zidentyfikować pojedynczego klienta i jego koszyk zakupów. W takim przypadku, z każdym rekordem opisującym zakupy pojedynczego klienta jest związana, dodatkowo, informacja o kliencie (identyfikator klienta) i o dacie zakupów (etykieta czasowa rekordu). Zbiór wszystkich rekordów w bazie danych opisujących zakupy danego klienta, uporządkowany zgodnie z wartościami etykiet czasowych tych rekordów, nazywamy sekwencją klienta i stanowi ona opis zachowania konsumenckiego tego klienta w czasie. Analizując sekwencje klientów w bazie danych możemy znaleźć typową sekwencję zakupów i, na tej podstawie, przewidywać przyszłe zachowania klientów: „klient, który miesiąc temu zakupił dużą partię cegieł o rozmiarze 25 cm, w ciągu tygodnia zakupi jeszcze, dodatkowo, partię cegieł o rozmiarze 11 cm”. Metodę odkrywania wzorców sekwencji stosuje się w analizie kataklizmów (trzęsienia ziemi, huragany, erupcje wulkanów) w celu określenia typowej sekwencji zdarzeń prowadzących do wystąpienia kataklizmu. W telekomunikacji metodę odkrywania wzorców sekwencji stosuje się do analizy sygnałów alarmowych urządzeń sieciowych w celu znalezienia zależności pomiędzy wystąpieniami tych sygnałów i określenia na tej podstawie źródła uszkodzenia w sieci. W ostatnim czasie operatorzy telefonii komórkowej wykorzystują metody odkrywania wzorców sekwencji do określania wzorców zachowań klientów, którzy przenoszą się do innych operatorów. Metody te są również szeroko stosowane w bankowości i ubezpieczeniach do analizy zachowań klientów i wykrywania oszustw ubezpieczeniowych. Ważnym obszarem zastosowań metod odkrywania wzorców sekwencji jest medycyna, gdzie metody te, przykładowo, wykorzystuje się do (1) określania efektywności terapii leczenia, (2) w diagnostyce medycznej do określania zależności pomiędzy występowaniem określonych symptomów chorobowych a jednostkami chorobowymi, wreszcie, (3) do analizy kosztów leczenia i wykrywania fałszerstw medycznych (żądania zwrotu nienależnych kosztów leczenia, fałszywych recept, itp.). Wreszcie, metody te znalazły szerokie zastosowanie do analizy efektywności i organizacji serwerów Web. Odkrywając wzorce sekwencji dostępu do stron WWW, przez eksplorację logu serwera WWW, można poprawić organizację logiczną serwera, zreorganizować sposób nawigacji po stronach WWW (poprawić i uprościć strukturę połączeń pomiędzy skorelowanymi stronami), czy też poprawić sposób prezentacji reklam (tzw. adaptatywne serwery WWW) dynamicznie dostosowując prezentację reklam do określonych grup użytkowników.
Klasyfikacja problemu

W zakresie odkrywania wzorców sekwencji możemy de facto wyróżnić trzy oddzielne problemy. Pierwszym problemem jest znajdowanie zależności pomiędzy występowaniem określonych zdarzeń w czasie czyli „znajdowanie wzorców sekwencji”. Problem ten możemy sformułować w następujący sposób: ‘Mamy daną bazę danych zawierającą sekwencję zdarzeń, które są opisane danymi kategorycznymi – znajdź wszystkie częste podsekwencje zdarzeń’.

Kolejny problem to problem znajdowania częstych epizodów sekwencji. Problem ten możemy scharakteryzować następująco: ‘Dana jest sekwencja i pewna klasa epizodów (klasa sekwencji zdarzeń), znajdź w zadanej sekwencji wszystkie częste epizody’. Ostatni problem reprezentuje problem analizy przebiegów czasowych. Problem ten możemy określić w następujący sposób: ‘Dana jest baza danych przebiegów czasowych (sekwencji zdarzeń opisanych danymi ciągłymi), znajdź przebiegi czasowe podobne do zadanego przebiegu, znajdź cykle w przebiegach czasowych, itp.’
Definicje i pojęcia podstawowe

W dalszej części wykładu skoncentrujemy się na pierwszym z wymienionych problemów, mianowicie na problemie znajdowania wzorców sekwencji. Aby móc dalej zagłębić się w problematykę odkrywania wzorców sekwencji, zapoznajmy się z podstawowymi pojęciami i definicjami jakimi będziemy się posługiwać w dalszej części wykładu.
Niech I = {i1, i2,..., im} oznacza zbiór literałów, nazywanych dalej elementami.
Transakcja T będzie zbiorem elementów, takich że T całkowicie zawiera się w I.
Sekwencją S nazywać będziemy uporządkowaną listę S = <T1;T2;...,Tn>, gdzie Ti zawiera się całkowicie w I, i = 1,2, ...,n, i Ti nie jest zbiorem pustym. Zbiór Ti zawiera się w S, oznaczony (x1; x2;...; xl), gdzie xj należy do I, 1<= j<= l, nazywać będziemy wyrazem sekwencji.
Dowolny element xj może wystąpić tylko raz w pojedynczym wyrazie sekwencji S, może natomiast wystąpić wielokrotnie w wielu wyrazach danej sekwencji S. Mówimy, że wyraz T sekwencji S wspiera element x należący do I, jeżeli x należy do T. Mówimy też, że wyraz T sekwencji S wspiera zbiór X całkowicie zawiera się w I, jeżeli T wspiera każdy element ze zbioru X.

Zbiór X, którego wsparcie jest większe od zadanej minimalnej wartości progowej minsup nazywamy zbiorem częstym.
Długością sekwencji S, oznaczoną length(S), nazywać będziemy liczbę wyrazów w S. Przykładowo, length( (7), (3 8), (9), (4 5 6), (8)) = 5.
Sekwencję o długości k nazywać będziemy k-sekwencją.
Rozmiarem sekwencji S, oznaczonym size(S), nazywać będziemy liczbę wystąpień instancji elementów w S. Przykładowo, size( (7), (3 8), (9), (3 5 6), (8)) = 8.

Mówimy, że sekwencja S1 ( a1, a2 ... an) zawiera się w innej sekwencji S2(b1, b2 ... bm) jeżeli istnieją takie liczby całkowite i1 < i2 < ... < in takie, że zachodzi a1 całkowicie zawiera się w bi1, a2 całkowicie zawiera się w bi2, ..., an całkowicie zawiera się w bin.
Przykładowo, sekwencja ( (B), (D E) ) zawiera się w sekwencji ( (A), (B), (C), (D A E), (C)), ponieważ (B) całkowicie zawiera się w (D, E) całkowicie zawiera się w (D A E). Sekwencja ( (A), (B)) nie zawiera się w sekwencji (A B) i vice versa.

Mówimy, że sekwencja S jest
maksymalna , jeżeli nie zawiera się w żadnej innej sekwencji.
Pod pojęciem sekwencji rozumieć będziemy listę transakcji uporządkowanych zgodnie z czasem ich realizacji.

W dalszej części wykładu będziemy rozważać bazę danych sekwencji DS nazywać będziemy zbiór sekwencji S, takich że DS = (S1, S2, ..., Sn). Mówimy, że sekwencja S należąca do bazy danych sekwencji DS, wspiera sekwencję Q, jeżeli Q zawiera się w sekwencji S.
Wsparciem sekwencji S = (X1, X2 ... Xn) w bazie danych sekwencji DS, oznaczonym wsparcie (S, DS), nazywać będziemy iloraz liczby
sekwencji należących do DS, które wspierają sekwencję S, do liczby wszystkich sekwencji należących do DS.
Sformułowanie problemu

Możemy obecnie przejść do oficjalnego sformułowania problemu odkrywania wzorców sekwencji. Celem procesu odkrywania wzorców sekwencji jest znalezienie wszystkich sekwencji, których wsparcie w bazie danych sekwencji DS przekracza pewną zadaną wartość minimalną, oznaczoną minsup. Sekwencje, które spełniają powyższy warunek minimalnego wsparcia, nazywamy sekwencjami częstymi lub wzorcami sekwencji. Sekwencje częste, które są maksymalne, nazywać będziemy maksymalnymi wzorcami sekwencji.
Przykład

Rozważmy przykładową bazę danych przedstawioną na slajdzie w tabeli Recepty. Baza danych zawiera informacje o: pacjentach (pacjentId),
receptach (receptaId), dacie wypisania recepty (data) oraz zapisanych lekach (lekId). Interpretacja tabeli jest następująca, rozważmy pierwszy rekord przedstawiony w tabeli. Rekord ten przedstawia sytuację, że 26 stycznia 1998 roku pacjent o identyfikatorze 105 otrzymał receptę 112 na lek o identyfikatorze 30. Kilka dni później, czyli 28 stycznia 1998 roku ten sam pacjent o identyfikatorze 105 otrzymał kolejną receptę 114 na lek o identyfikatorze 90. Przykładowo pacjent o identyfikatorze 200 otrzymał recepty o identyfikatorze 117 w dniu 3/9/98 na następujące leki: lek o identyfikatorze 30, lek o identyfikatorze 50 oraz lek o identyfikatorze 70. Przedstawioną bazę danych można przedstawić w postaci bazy danych sekwencji, w której kolejność występowania zdarzeń jest reprezentowana poprzez uporządkowanie wyrazów sekwencji. W tym przypadku zdarzeniem jest wypisanie recepty pojedynczemu pacjentowi na określony zbiór leków. Analizując bazę danych sekwencji można w niej odkryć, zakładając próg minimalnego wsparcia minsup = 0.25, następujące cztery wzorce sekwencji:
-
((30), (40) sup = 0,4
-
((30), (70) sup = 0,4
-
((30), (90)) sup = 0,4
-
((30), (40 70)) sup = 0,4
-
Wzorce (3) i (4) są maksymalnymi wzorcami sekwencji. Interpretacja odkrytych wzorców sekwencji jest następująca. W 40% przypadków
lekarze zapisują lek 30, a następnie, lek 90. Inną popularną terapią stosowaną przez lekarzy (40% przypadków) jest stosowanie leku 30, a następnie, pary leków 40 i 70.
Podstawowy algorytm odkrywania wzorców sekwencji GSP

Pierwszy algorytm odkrywania wzorców sekwencji przedstawiono w roku 1995. Algorytm ten, nazwaliśmy "podstawowym algorytmem odkrywania wzorców sekwencji", jest on rozszerzeniem klasycznego algorytmu Apriori dla danych sekwencyjnych i wykorzystuje własność monotoniczności miary wsparcia: jeżeli sekwencja X nie jest wzorcem sekwencji (tj. nie spełnia warunku minimalnego wsparcia), to żadna sekwencja Y, zawierająca sekwencję X, nie może być wzorcem sekwencji.
Algorytm składa się z pięciu następujących kroków:
Krok 1 – sortowanie. Posortuj bazę danych D w taki sposób, aby uzyskać bazę danych sekwencji DS.
Krok 2 - znajdowanie zbiorów częstych. Znajdź wszystkie zbiory częste w bazie danych sekwencji DS.
Krok 3 – transformacja. Przetransformuj każdy wyraz sekwencji w listę zbiorów częstych zawierających się w tym wyrazie.
Krok 4 – sekwencjonowanie. Znajdujemy wszystkie częste sekwencje.
Krok 5 – maksymalizacja. – jest krokiem opcjonalnym i polega na usunięciu wszystkich wzorców sekwencji, które nie są maksymalne.
Krok 1: sortowanie
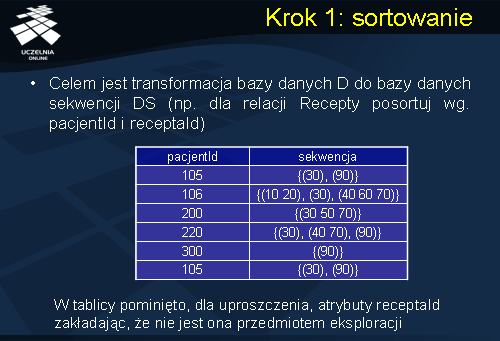
Obecnie przejdziemy do omówienia poszczególnych kroków podstawowego algorytmu odkrywania wzorców sekwencji. Rozpoczniemy od kroku pierwszego – czyli kroku sortowania. Celem tego kroku jest transformacja oryginalnej bazy danych D do bazy danych sekwencji DS. Transformacja ta wymaga posortowania bazy danych D w taki sposób, aby można było ją przetransformować do postaci bazy danych sekwencji DS. Sposób sortowania zależy od charakterystyki bazy danych D. W naszym przykładzie transformacja wymaga posortowania bazy danych D według atrybutów Pacjent_id (w tablicy pominięto, dla uproszczenia, atrybut receptaId zakładając, że nie jest ona przedmiotem eksploracji). Następnie, rekordy reprezentujące danego pacjenta, uporządkowane według rosnących wartości atrybutu data, były transformowane do postaci sekwencji wyrazów. Wynikiem tego kroku jest baza danych sekwencji DS. przedstawiona na slajdzie.
Krok 2: znajdowanie zbiorów częstych

Kolejnym krokiem algorytmu jest krok 2 – znajdowania zbiorów częstych. Celem tego kroku jest znalezienie wszystkich zbiorów częstych w bazie danych sekwencji DS. Do tego celu można zastosować dowolny algorytm znajdowania zbiorów częstych (na przykład, algorytm Apriori). W przeciwieństwie do algorytmu Apriori, w kroku znajdowania zbiorów częstych wsparcie danego zbioru X jest obliczane względem liczby sekwencji, a nie liczby transakcji (wyrazów sekwencji). Wsparciem zbioru X w bazie danych sekwencji DS jest iloraz liczby sekwencji zawierających wyrazy wspierające zbiór X do całkowitej liczby sekwencji należących do bazy danych sekwencji DS. Przykładowo, jeżeli baza danych sekwencji zawiera dwie sekwencje: sekwencja 1: ((A, B) (B, C) (C, D)) oraz sekwencja 2: ((A, B) (B, C, D)) to wsparcie zbioru (A, B) wynosi 100%, gdyż obie sekwencje zawierają wyrazy wspierające zbiór (A, B).
Krok 3: transformacja

Kolejnym krokiem algorytmu jest krok transformacji. Celem kroku transformacji jest zastąpienie każdego wyrazu T sekwencji S w uporządkowaną listę zbiorów częstych zawierających się w wyrazie T. W wyniku tej transformacji są usuwane z wyrazu T wszystkie te elementy, które nie są częste i które, tym samym, nie mogą wystąpić we wzorcach sekwencji. Jeżeli sekwencja nie zawiera żadnych zbiorów częstych, to nie wchodzi ona do transformowanej bazy danych. Brana jest ona jednak pod uwagę przy obliczaniu wsparcia wzorca sekwencji. Stąd, po zakończeniu kroku transformacji, każda sekwencja jest reprezentowana w bazie danych sekwencji DS w postaci uporządkowanej listy wyrazów będących zbiorami częstymi. Stąd dla naszego przykładu musimy wykonać następujące kroki: Przetransformuj każdy wyraz sekwencji w listę zbiorów częstych zawierających się w tym wyrazie, następnie przetransformuj każdy zbiór częsty w liczbę naturalną. Ma to na celu uproszczenie obliczeń. Dla ilustracji tego kroku rozważmy następujący przykład umieszczony na slajdzie. Załóżmy, że dane są następujące zbiory częste {{A},{B},{C},{BC}} znalezione w bazie sekwencji DS. Załóżmy, że przyjęliśmy następujące odwzorowanie – zbiór częsty {A} jest reprezentowany przez liczbę naturalną 1, zbiór częsty {B} jest reprezentowany przez liczbę naturalną 2, zbiór częsty {C} jest reprezentowany przez liczbę naturalną 3 oraz zbiór częsty {BC} reprezentowany przez liczbę 4. Dla podanej oryginalnej sekwencji postaci: {{D},{A},{(B E C)}}. Zauważmy, że wyraz pierwszy tej sekwencji zawiera element D, który nie jest zbiorem częstym – dlatego zostanie usunięty z naszej sekwencji. Kolejny wyraz A jest zbiorem częstym, pozostaje w naszej sekwencji, itd. W wyniku transformacji otrzymamy następującą sekwencję dwuwyrazową: {{(A)}, {(B), (C), (B C)}} oraz sekwencja po odwzorowaniu: {{1},{2, 3, 4}}.
Krok 4: sekwencjonowanie

Kolejnym krokiem algorytmu jest krok sekwencjonowania. Celem kroku sekwencjonowania jest znalezienie wszystkich sekwencji częstych. Punktem wyjścia procedury przedstawionej na slajdzie implementującej krok 4 są wszystkie sekwencje częste o długości 1. Sekwencje te są wynikiem działania kroku drugiego. Następnie realizowana jest pętla for, rozpoczynamy od k=2. Generowane są wszystkie sekwencje kandydujące o długości 2 w oparciu o zbiór wszystkich sekwencji częstych o długości 1. Do generowania sekwencji kandydujących o długości 2 wykorzystywana jest funkcja Apriori-generate(). Następnie dla każdej sekwencji S należącej do bazy danych sekwencji DS, zwiększamy licznik wszystkich sekwencji kandydujących należących do CS2, zawierających się w sekwencji S. Pętla jest powtarzana tak długo jak długo zbiór sekwencji częstych o długości k jest różny od zbioru pustego. Wynikiem działania tej procedury jest zbiór wszystkich sekwencji częstych o długości 1,2,3,…,k.

Kluczowe znaczenie w procedurze implementującej krok 4 - sekwencjonowania ma funkcja Apriori_generate(). Funkcja ta generuje k-sekwencje kandydujące w dwóch etapach: W pierwszym etapie połączenia - funkcja wykonuje operację połączenia dwóch sekwencji ze zbioru LSk-1 (czyli wszystkich sekwencji częstych o długości k-1) w celu wygenerowania k-sekwencji kandydującej; warunkiem połączenia dwóch sekwencji LSk-1 jest zgodność pierwszych (k-2) wyrazów obu sekwencji. Drugi etap eliminacji - funkcja Apriori_generate() usuwa wszystkie sekwencje S zawarte w CSk takie, dla których istnieją (k-1)-podsekwencje sekwencji S nie należące do zbioru sekwencji częstych o długości k-1 (LSk-1).
Funkcja Apriori-generate

W jaki sposób jest realizowany krok połączenia funkcji Apriori_generate()? Otóż łączymy dwie sekwencje częste o długości k-1 w celu uzyskania sekwencji kandydującej o długości k, według następującego warunku połączeniowego: można połączyć dwie sekwencje częste o długości k-1 jeżeli pierwszych k-2 wyrazów obu sekwencji jest identyczny. Zwróćmy uwagę, że porządek wyrazów nie jest przestrzegany i sekwencja może być łączona ze sobą (tzw. selfjoin). Krok odcięcia wygląda podobnie ja w przypadku funkcji Apriori_gen() - gdzie zostają usunięte wszystkie sekwencje kandydujące, które posiadają nieczęste podsekwencje.
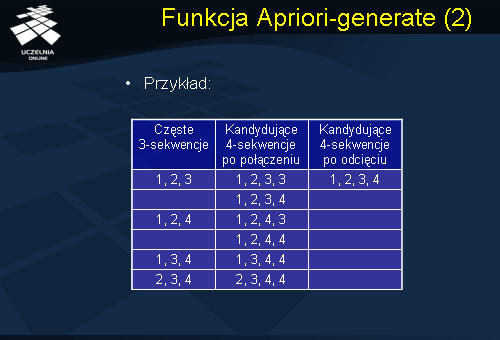
Przykład przedstawiony na slajdzie ilustruje działanie funkcji Apriori-generate(), która w dwóch krokach (połączenia i odcięcia) generuje kandydatów w oparciu o sekwencje częste. Dany jest zbiór częstych sekwencji o długości 3 przedstawiony na slajdzie, są to następujące sekwencje: {1,2,3},{1,2,4},{1,3,4},{2,3,4}. W wyniku pierwszego kroku działania funkcji Apriori_generate() otrzymujemy zbiór sekwencji kandydujących o długości 4 przedstawiony na slajdzie. Zauważmy, że sekwencję częstą o długości 3 - {1,2,3} możemy połączyć ze sobą, uzyskamy wówczas sekwencję kandydującą o długości 4 - {1,2,3,3} oraz sekwencję {1,2,3} możemy połączyć z sekwencją częstą o długości 3 z sekwencją {1,2,4}. Uzyskamy wówczas sekwencję kandydującą o długości 4 postaci {1,2,3,4}. Następnie sekwencję częstą {1,2,4} łączymy z sekwencją {1,2,3} i uzyskujemy sekwencję kandydująca o długości 4 postaci {1,2,4,3}. Sekwencję częstą {1,2,4} możemy połączyć ze sobą i wówczas otrzymamy sekwencję kandydująca postaci {1,2,4,4}. Sekwencję {1,3,4} możemy połączyć tylko ze sobą i wówczas otrzymamy sekwencję kandydująca postaci o długości 4 {1,3,4,4}, podobnie w przypadku sekwencji częstej {2,3,4} łączymy ją ze sobą i otrzymujemy sekwencję kandydującą o długości 4 postaci {2,3,4,4}. W drugim kroku, funkcja usuwa wszystkie sekwencje kandydujące, o długości 4, które posiadają nieczęste podsekwencje. W wyniku czego otrzymujemy 1 sekwencję kandydującą o długości 4 postaci {1,2,3,4}.
Krok 5: maksymalizacja

Prezentowany slajd przedstawia ostatni krok algorytmu odkrywania wzorców sekwencji – kroku maksymalizacji. Celem kroku maksymalizacji, który jest krokiem opcjonalnym, jest znalezienie w zbiorze wszystkich wzorców sekwencji, tych wzorców sekwencji, które są maksymalne. Dany jest zbiór wszystkich wzorców sekwencji S znalezionych w kroku sekwencjonowania. Następujący algorytm usuwa ze zbioru S wszystkie sekwencje, które nie są maksymalne (n oznacza długość najdłuższej sekwencji ze zbioru S). W wyniku tego kroku otrzymujemy wszystkie maksymalne wzorce sekwencji.
Przykład 2
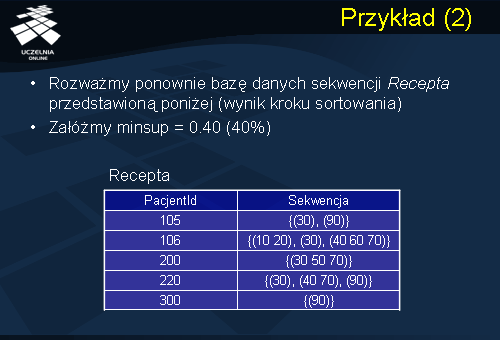
Dla ilustracji działania algorytmu odkrywania wzorców sekwencji rozważmy prosty przykład przedstawiony na kolejnych slajdach. Przykład odnosi się do bazy danych sekwencji Recepta, którą analizowaliśmy wcześniej (slajd Przykład (1)). Jak pamiętamy pierwszym krokiem algorytmu odkrywania wzorców sekwencji jest krok sortowania czyli transformacja oryginalnej bazy danych do bazy danych sekwencji. Wynikiem tego kroku jest baza danych sekwencji Recepta umieszczona na powyższym slajdzie. Zakładamy minimalny próg wsparcia = 40%.
Przykład 3
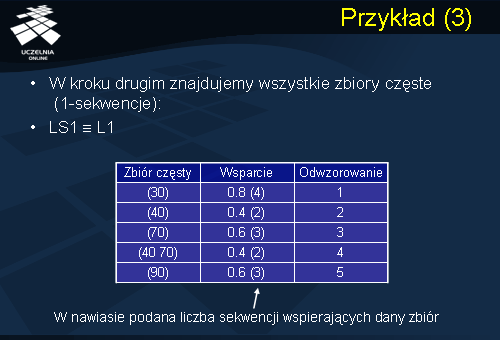
Przechodzimy do kroku drugiego znajdowania wszystkich zbiorów częstych. Zbiory częste odpowiadają w tym przypadku wszystkim sekwencjom częstym o długości 1. Pamiętamy, że w przeciwieństwie do algorytmu Apriori, w kroku znajdowania zbiorów częstych wsparcie danego zbioru X jest obliczane względem liczby sekwencji, a nie liczby transakcji (wyrazów sekwencji). Wsparciem zbioru X w bazie danych sekwencji Recepty jest iloraz liczby sekwencji zawierających wyrazy wspierające zbiór X (zbiór częsty) do całkowitej liczby sekwencji należących do bazy danych sekwencji Recepty. Rozpoczynamy od zbioru C1, czyli analizujemy wsparcie wszystkich elementów występujących w bazie danych. Zbiór elementów składa się z następujących elementów: {10},{20},{30},{40},{50},{60},{70} oraz {90}. Dla każdego zbioru jednoelementowego kandydującego obliczamy jego wsparcie. Okazuje się, że zbiorami częstymi 1-elementowymi są następujące zbiory: zbiór {30},{40},{70},{90}. Zwróćmy uwagę na wsparcie dla zbioru {30}. Wsparcie to wynosi 0.8 i jest to liczba pacjentów, którym zapisano lek 30 na jednej z wielu recept, które otrzymał on od lekarza do całkowitej liczby pacjentów. Następnie w oparciu o zbiory częste jednoelementowe są generowane zbiory kandydujące 2-elementowe. Takimi zbiorami są zbiory {30,40},{30,70},{30,90},{40,70},{40,90} oraz {70,90}. Obliczamy wsparcie zbiorów kandydujących 2-elementowych i okazuje się, że tylko jeden zbiór kandydujący {40,70} spełnia próg minimalnego wsparcia. To kończy krok znajdowania wszystkich zbiorów częstych. Znalezione w tym kroku zbiory częste są odwzorowywane w zbiór liczb naturalnych lub całkowitych przedstawionych w powyższej tabeli nazwanej kolumną Odwzorowania. Transformacja ta ma na celu poprawę efektywności algorytmu poprzez skrócenie czasu wykonywania operacji porównywania zbiorów.
Przykład 4

Następnie dokonujemy transformacji bazy danych sekwencji do bazy danych sekwencji zawierających wyrazy składające się wyłącznie ze zbiorów częstych. W ten sposób usuwane są wszystkie te elementy, które nie są częste i tym samym, nie mogą wystąpić we wzorcach sekwencji. Jak powiedzieliśmy wcześniej, jeżeli sekwencja nie zawiera żadnych zbiorów częstych, to nie wchodzi ona do transformacji bazy danych. Brana jest ona jednak pod uwagę przy obliczaniu wsparcia wzorca sekwencji. Stąd, po zakończeniu kroku transformacji, każda sekwencja jest reprezentowana w bazie danych sekwencji DS w postaci uporządkowanej listy wyrazów z których każdy jest listą wyrazów będących zbiorami częstymi. Rozważmy przykład przedstawiony na slajdzie. Zacznijmy od sekwencji początkowej {(30),(90)}. Zauważmy, że pierwszy wyraz, który składa się ze zbioru częstego {30} nie zawiera elementów, które nie są częste zatem wyraz ten nie podlega transformacji i przechodzi do Sekwencji po transformacji. Podobnie z wyrazem drugim {90}, w konsekwencji sekwencja po transformacji ma postać {(30),(90)}, po odwzorowaniu {(1),(5)}. Rozważmy druga sekwencję trzywyrazową, która ma postać{(10 20),(30),(40 60 70)}. Pierwszy wyraz składa się z elementów które nie są częste, zarówno element {10} jak i {20} nie jest elementem częstym. Zatem usuwamy pierwszy wyraz sekwencji. Drugi wyraz jest zbiorem częstym {30}. Trzeci wyraz zawiera zbiór kilku elementów, element {60} nie jest częsty dlatego zostaje usunięty. Pozostają elementy {(40 70)}, zauważmy, że element {40},{70} oraz {(40 70)} są zbiorami częstymi. Stąd, ten wyraz sekwencji początkowej jest transformowany do listy zbiorów częstych następującej postaci {(30),(40),(70),(40 70)}. Po odwzorowaniu otrzymujemy sekwencję po odwzorowaniu {(1),(2,3,4)}. Podobnie postępujemy z pozostałymi sekwencjami.
Przykład 5
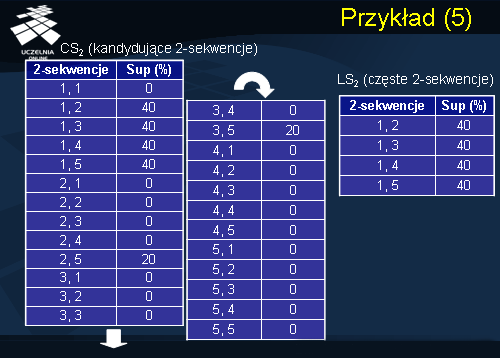
Następnie generowane są sekwencje kandydujące o długości 2 w oparciu o zbiór sekwencji częstych o długości 1. Zauważmy, że zbiór wszystkich sekwencji kandydujących o długości 2 jest zbiorem wszystkich możliwych kombinacji zbioru sekwencji o długości 1. Zatem mamy sekwencję {(1),(1)},{(1),(2)},{(1),(3)} itd. Następnie dla każdej sekwencji kandydującej o długości 2 obliczamy jej wsparcie. Wszystkie sekwencje kandydujące, których wsparcie nie spełnia progu minimalnego wsparcia są eliminowane. W wyniku kroku drugiego otrzymujemy zbiór sekwencji częstych o długości dwa przedstawionych na slajdzie. Zbiór ten składa się z następujących sekwencji {(1),(2)},{(1),(3)},{(1),(4)}{(1),(5)}. Wsparcie wszystkich tych sekwencji wynosi 40%.
Przykład 6
Przechodzimy następnie do generacji zbiorów sekwencji kandydujących o długości 3. Okazuje się, że zbiór sekwencji kandydujących o długości 3 jest zbiorem pustym, gdyż w oparciu o zbiór sekwencji LS2 czyli zbiór sekwencji częstych o długości 2 nie można wygenerować żadnych sekwencji kandydujących. Wyjaśnienie tego jest następujące - w pierwszym etapie funkcji Apriori_generate() czyli etapie połączenia ze zbioru LS2 generowany jest następujący zbiór sekwencji kandydujących o długości 3, mianowicie z sekwencji {1,2} otrzymujemy sekwencje {1,2,2},{1,2,3},{1,2,4} oraz {1,2,5}, następnie {1,3,2},{1,3,3},{1,3,4},{1,3,5}, następnie {1,4,2},{1,4,3},{1,4,4},{1,4,5}. Wreszcie z ostatniej sekwencji kandydującej otrzymujemy {1,5,2},{1,5,3},{1,5,4},{1,5,5}. Jednakże żadna z wygenerowanych sekwencji o długości 3 nie wchodzi do zbioru sekwencji kandydujących o długości 3, gdyż każda z podanych wcześniej sekwencji kandydującej o długości 3 zawiera sekwencje o długości 2, która nie należy do zbioru sekwencji częstych o długości 2. W konsekwencji zbiór CS3 czyli zbiór o długości 3 jest zbiorem pustym, w konsekwencji zbiór sekwencji częstych LS3 również jest zbiorem pustym. Końcowym zbiorem wyniku sekwencjonowania jest zatem zbiór LS2.
W ten sposób otrzymujemy zbiór wzorców sekwencji:
(30), (40) wsparcie 0,4 (40%)
(30), (70) wsparcie 0,4 (40%)
(30), (90) wsparcie 0,4 (40%)
(30), (40 70) wsparcie 0,4 (40%)
Następnie możemy wykonać ostatni krok algorytmu, który jest krokiem opcjonalnym czyli krok maksymalizacji. W otrzymanym zbiorze częstych wzorców sekwencji znajdujemy te wzorce sekwencji, które są maksymalne. Łatwo zauważyć, że sekwencja {(30),(40)} oraz sekwencja {(30),(70)} nie są sekwencjami maksymalnymi gdyż zawierają się w sekwencji {(30)(40 70)}. Ostateczny zbiór maksymalnych wzorców sekwencji dla zadanego progu minsup=25% składa się z dwóch wzorców:
(30), (90) wsparcie 0,4 (40%)
(30), (40 70) wsparcie 0,4 (40%)
























