
W przypadku niektórych dziedzin zastosowań metody odkrywania wzorców sekwencji, takich jak analiza łańcuchów DNA czy też analiza akcji giełdowych, liczba odkrywanych wzorców sekwencji może być relatywnie bardzo duża. Co więcej, również odkrywane sekwencje mogą być bardzo długie. Stąd, pojawiła się potrzeba opracowania nowych skalowalnych algorytmów odkrywania wzorców sekwencji, które wykorzystując podstawową własność ogólnego algorytmu odkrywania wzorców sekwencji (monotoniczność miary wsparcia), redukowałyby kosztowność etapu sekwencjonowania i gwarantowałyby tym samym znacznie większą efektywność i skalowalność procesu odkrywania wzorców sekwencji. Powstały nowe pomysły i algorytmy, które rozwiązywałyby te problemy. Algorytm o nazwie FreeSpan, który w procesie odkrywania wzorców sekwencji wykorzystuje ideą projekcji bazy danych na osobne partycje w celu zredukowania czasu generowania sekwencji kandydujących i obliczania wsparcia tych sekwencji. Ogólna idea algorytmu polega na wykorzystaniu zbiorów częstych do rekursywnej dekompozycji bazy danych na mniejsze partycje i generowaniu sekwencji kandydujących w ramach każdej partycji. W konsekwencji, algorytm generuje znacznie mniejszy zbiór sekwencji kandydujących i uzyskuje istotną poprawę efektywności w stosunku do przedstawionego podstawowego algorytmu odkrywania wzorców sekwencji. Rozwinięciem algorytmu FreeSpan jest algorytm PrefixSpan. Ogólna idea algorytmu PrefixSpan polega na analizie prefiksów sekwencji kandydujących i rekursywnym partycjonowaniu bazy danych w oparciu o postfiksy generowanych sekwencji. Algorytm PrefixSpan uzyskuje dodatkową poprawę efektywności w stosunku do algorytmu FreeSpan poprzez redukcję rozmiarów partycjonowanych baz danych i zmniejszenie liczby analizowanych sekwencji kandydujących. Algorytm PrefixSpan generuje rekursywnie wzorce sekwencji o rozmiarze k w oparciu o wzorce sekwencji o rozmiarze (k-1), i, de facto, nie generuje ani też nie analizuje sekwencji kandydujących. Algorytm PrefixSpan składa się z trzech kroków. W pierwszym kroku następuje znajdowanie wzorców sekwencji o rozmiarze 1. W drugim kroku dzielimy przestrzeń poszukiwań na partycje. Krok trzeci to analiza podzbiorów sekwencji przechowywanych w partycjach.
Znajdowanie wzorców sekwencji o długości 1

Omówimy krótko poszczególne kroki algorytmu PrefixSpan. Idea algorytmu polega na zastąpieniu etapu sekwencjonowania, polegającego na generowaniu sekwencji kandydujących i, następnie, sprawdzaniu, czy dana sekwencja kandydująca spełnia warunek minimalnego wsparcia, etapem polegającym na budowie i analizie prefiksów sekwencji należących do bazy danych sekwencji. Tak jak wspomnieliśmy wcześniej, w pierwszym kroku algorytmu PrefixSpan znajdujemy wzorce sekwencji DS o długości 1 i rozmiarze 1. Wykonujemy jednokrotny odczyt bazy danych sekwencji DS w celu znalezienia wszystkich sekwencji częstych jednoelementowych (czyli sekwencji o rozmiarze 1) o długości 1. Sekwencje częste o długości 1, które zawierają więcej elementów, na przykład sekwencja <(a,b)>, są znajdowane w kolejnych krokach algorytmu.

Do opisu sekwencji częstych będziemy stosować następującą notację: (sekwencja): licznik wsparcia. Przykładowo wyrażenie (a): 4 oznaczać będzie sekwencję a, której licznik wsparcia wynosi 4. W tym kroku transformujemy również bazę danych sekwencji DS do postaci bazy danych sekwencji DS z której usunięto wszystkie elementy, które nie są częste. Elementami częstymi są tylko i wyłącznie jednoelementowe sekwencje częste o długości 1. W tym kroku transformujemy również bazę danych sekwencji DS do postaci bazy danych sekwencji D{TS}, z której usunięto wszystkie elementy, które nie są częste.
Dzielenie przestrzenie poszukiwań na partycje

W kroku drugim algorytmu PrefixSpan przestrzeń wszystkich możliwych wzorców sekwencji można podzielić na n partycji (projekcyjnych baz danych), gdzie n odpowiada liczbie jednoelementowych sekwencji częstych o długości 1 znalezionych w kroku poprzednim. Wynika to ze spostrzeżenia, że dowolny wzorzec sekwencji musi, z definicji, rozpoczynać się od jednej ze znalezionych 1-sekwencji częstych jednoelementowych.
Analiza podzbiorów sekwencji przechowywanych w partycjach

Kolejnym krokiem algorytmu jest krok analizy podzbiorów sekwencji przechowywanych w partycjach. Dla każdej jednoelementowej sekwencji częstej o długości 1 tworzymy projekcyjną bazę danych jej postfiksów. Każda z tych baz danych jest następnie rekurencyjnie eksplorowana w celu wygenerowania wzorców sekwencji. Eksploracja polega na znajdowaniu wieloelementowych sekwencji częstych o długości 1 lub sekwencji częstych o długości 2, utworzeniu kolejnych projekcyjnych baz danych dla znalezionych sekwencji częstych, eksploracji tych baz danych, itd.
PrefixSpan

Prześledźmy teraz poszczególne kroki algorytmu PrefixSan na przykładzie umieszczonym na slajdzie. Mamy posortowaną bazę danych sekwencji, przedstawiona na slajdzie. Algorytm PrefixSpan wykonuje się w dwóch krokach. Krok pierwszy – znajdujemy 1-elementowe wzorce sekwencji o długości 1, będą to <a>, <b>, <c>, <d>, <e>, <f>. W następnym kroku dzielimy zbiór sekwencji na partycje. Otrzymujemy 6 partycji, pierwsza z prefiksem <a> … ostatnia z prefiksem <f>.
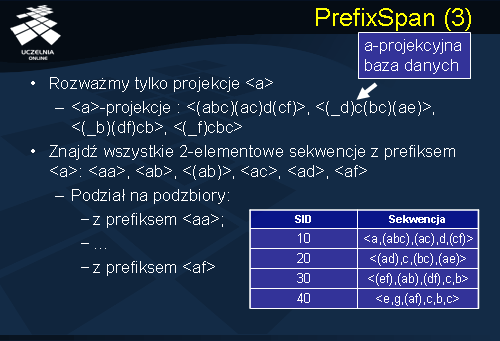
Rozważmy partycję związaną z prefiksem <a>. Zbiór wszystkich postfiksów prefiksu <a>, czyli zbiór wszystkich sekwencji rozpoczynających się od <a> tworzą tzw. a-projekcyjną bazę danych. A-projekcyjna baza danych została przedstawiona na slajdzie. Następnie poszukujemy wszystkich sekwencji 2-elementowych z prefiksem <a>. Będą to sekwencje: <a>: <aa>, <ab>, <(ab)>, <ac>, <ad>, <af>. Dzielimy następnie a-projekcyjną bazę danych na podzbiory z prefiksem <aa>, <ab> aż do podzbioru <af>.

Jak powiedzieliśmy podczas jednokrotnego odczytu a-projekcyjnej bazy danych znajdowane są wszystkie sekwencje częste o rozmiarze 2 i o długości 2, posiadające prefiks a, lub sekwencje częste o długości 1 i rozmiarze większym od 1, dla których element a należy do pierwszego wyrazu sekwencji częstej: <aa>, <ab>, <ac>, <ad>, .... <(ab)>. Dla każdej otrzymanej sekwencji częstej o długości 2 tworzymy kolejną projekcyjną bazę danych.
Kompletność algorytmu PrefixSpan
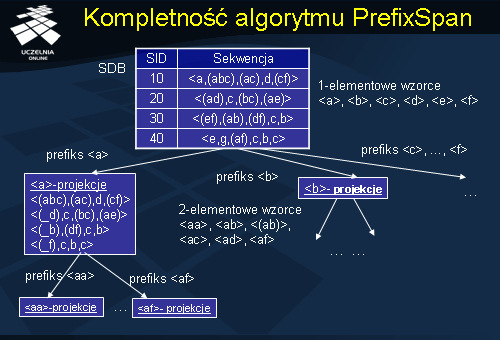
Zauważmy, że podstawowa idea algorytmu o której już wspominaliśmy polega na zastąpieniu etapu sekwencjonowania, który występuje w algorytmie GSP i który polega na generowaniu sekwencji kandydujących. Następnie sprawdzaniu czy dana sekwencja kandydująca spełnia warunki minimalnego wsparcia. Etapem czy sekwencją etapów polegających na budowie i analizie prefiksów sekwencji należących do bazy danych sekwencji. To znaczy w kolejnych krokach generujemy czy konstruujemy wzorce sekwencji. W pierwszym kroku algorytmu generujemy wzorce sekwencji o długości 1 i rozmiarze 1. W kolejnych krokach generujemy wzorce sekwencji o rozmiarze 2 i długości 1 lub wzorce sekwencji o długości 2. W kolejnych krokach konstruujemy wzorce sekwencji. W konsekwencji algorytm PrefixSpan generuje wszystkie możliwe wzorce sekwencji, które zawierają się w bazie danych sekwencji, a zatem algorytm PrefixSpan jest kompletny.
Efektywność algorytmu PrefixSpan

Jak pokazały badania ewaluacyjne, algorytm PrefixSpan charakteryzuje się znacznie wyższą efektywnością aniżeli podstawowy algorytm odkrywania wzorców sekwencji. Wynika to z dwóch zasadniczych przyczyn: po pierwsze w przeciwieństwie do podstawowego algorytmu odkrywania wzorców sekwencji, opartego na idei algorytmu Apriori, algorytm PrefixSpan nie generuje sekwencji kandydujących, lecz buduje sekwencje częste w sposób przyrostowy w oparciu o wcześniej odkryte sekwencje częste, oraz po drugie w ramach kroku „sekwencjonowania”, to jest znajdowania sekwencji częstych, algorytm PrefixSpan analizuje projekcyjne bazy danych, które są znacznie mniejsze od wyjściowej, oryginalnej bazy danych. Co więcej, w kolejnych iteracjach algorytmu, rozmiary tych baz danych znacząco maleją. Łatwo zauważyć jednak, że główny koszt algorytmu PrefixSpan kryje się w koszcie konstrukcji projekcyjnych baz danych. Gdyby można było zredukować rozmiar i\lub liczbę projekcyjnych baz danych generowanych przez algorytm, wówczas znacząco poprawiłoby to efektywność algorytmu. Jednym ze sposobów redukcji liczby i rozmiarów projekcyjnych baz danych generowanych przez algorytm PrefixSpan jest zastosowanie dwupoziomowego schematu projekcji (ang. bi-level projection).
Dwupoziomowy schemat projekcji

Przedstawimy obecnie mechanizm działania dwupoziomowego schematu projekcji. Prześledźmy sposób odkrywania sekwencji częstych wykorzystywany w algorytmie PrefixSpan uzupełniony o dwupoziomowy schemat projekcji. Pierwszy krok polega na odczycie bazy danych DS w celu znalezienia wszystkich jednoelementowych sekwencji częstych o długości 1. Znalezione sekwencje to: <a>, <b>, <c>, <d>, <e>, <f>. Następnie, transformujemy bazę danych sekwencji DS w bazę danych sekwencji DTS zawierającą wyłącznie sekwencje składające się z elementów częstych. W drugim kroku, zamiast konstruować projekcyjne bazy danych względem znalezionych prefiksów, konstruujemy macierz trójkątną S o wymiarach n x n (gdzie n oznacza liczbę jednoelementowych sekwencji częstych)

Macierz S zawiera informacje o wsparciu wszystkich sekwencji o długości i rozmiarze 2, oraz długości 1 i rozmiarze 2, skonstruowanych w oparciu o jednoelementowe sekwencje częste o długości 1. Elementy macierzy S leżące na przekątnej reprezentują wartości liczników wsparcia sekwencji o długości i rozmiarze 2. Możemy przeanalizować przykład S[a,a]=2 wskazuje, że sekwencja o długości 2 i rozmiarze 2 (a a) posiada wsparcie 2. Podobnie, licznik wsparcia sekwencji (b b) wynosi 1. Pozostałe elementy macierzy S nie leżące na przekątnej reprezentują trzy liczniki wsparcia.

Element macierzy S[a, b] = (x1, x2, x3) reprezentuje wartości licznika wsparcia, odpowiednio, sekwencja o długości 2 <(a),(b)>, sekwencja o długości 2 <(b),(a)> oraz sekwencja o długości 1 <(a b)>. Przykładowo: element S[a b] = (4, 2, 2) wskazuje, że licznik wsparcia sekwencji <(a),(b)> wynosi 4, licznik wsparcia sekwencji <(b),(a)> wynosi 2, i licznik wsparcia sekwencji <(a b)> wynosi 2. Zauważmy, że elementy macierzy leżące po obu stronach przekątnej zawierają identyczną informację: S[a, b] = S[b, a]. Dlatego też, do opisu wsparcia sekwencji wystarczy macierz trójkątna.
S-matrix

Rozważmy macierz S przedstawioną na slajdzie, skonstruowaną dla bazy danych sekwencji przedstawioną po lewej stronie slajdu. Rozważmy pierwszy element macierzy S o współrzędnych <aa>. Wartość tego elementu wynosi 2 – oznacza to, że sekwencja o długości 2 (sekwencja postaci <aa>) zawiera się w dwóch sekwencjach należących do bazy danych sekwencji. Łatwo zauważyć, że sekwencja <aa> jest podsekwencją sekwencji pierwszej o id 10 w bazie danych sekwencji oraz sekwencji drugiej o id równym 20. Rozważmy kolejny element macierzy S, element o współrzędnych <ac>. Zauważmy, że element <ac> posiada następujące wartości liczników wsparcia (4, 2, 1). Oznacza to, że sekwencja o długości 2 postaci <ac> jest wspierana przez 4 sekwencje z bazy danych sekwencji. Łatwo zauważyć, że wszystkie 4 sekwencje przedstawione na slajdzie czyli sekwencje o identyfikatorze 10, 20, 30 i 40 wspierają sekwencję <ac>. Sekwencja o długości 2 postaci <ca> wspierana jest przez 2 sekwencje należące do bazy danych sekwencji. Natomiast sekwencja o długości 1 składająca się ze zbioru (ac) wspierana jest tylko przez jedną sekwencję.
<ad> - projekcje
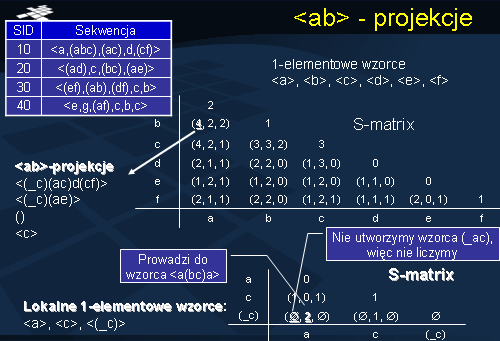
W kolejnym kroku dla każdej 2-elementowej sekwencji częstej a konstruujemy a-projekcyjną bazę danych. Rozważmy przykładowo sekwencję <ab>, która jak wynika z macierzy S jest sekwencją częstą. Zauważmy, że element o współrzędnych <ab> posiada wsparcie 4, tzn. wszystkie 4 sekwencje należące do bazy danych sekwencji przedstawionej na slajdzie wspierają tą podsekwencję. Następnie dla sekwencji <ab> tworzymy <ab> - projekcyjną bazę danych. ab-projekcyjna baza danych została przedstawiona na slajdzie poniżej bazy danych sekwencji po lewej stronie. Zauważmy, że baza ta zawiera 3 lokalne sekwencje częste 1-elementowe <a>, <c>, <_c>. W kolejnym kroku konstruujemy macierz S dla ab-projekcyjnej bazy danych. Zauważmy, że tutaj znajdujemy tylko i wyłącznie jedną sekwencję <_ca>, która jest częsta. Prowadzi to do wzorca sekwencji postaci <a, (bc), a>.
Zysk z "Bi-level Projection"

Można łatwo udowodnić, że przedstawiona metoda dwupoziomowej projekcji generuje poprawny zbiór wzorców sekwencji. Jednakże, aby wygenerować wszystkie wzorce sekwencji, (np..dla 53 wzorców), algorytm PrefixSpan wymaga skonstruowania 53 projekcyjnych baz danych. W przypadku metody dwupoziomowej projekcji, dla rozważanego przykładu, znalezienie wszystkich wzorców sekwencji wymaga skonstruowania 22 projekcyjnych baz danych.
Główne cechy algorytmu PrefixSpan

Jak już wcześniej zostało wspomniane algorytm PrefixSpan charakteryzuje się znacznie wyższą efektywnością aniżeli podstawowy algorytm odkrywania wzorców sekwencji. Należy on do algorytmów „pattern-growth”. Wyszukiwanie jest bardziej skupione a tym samym bardziej efektywne. Zauważmy, bowiem, że w miejsce, że w miejsce kroku sekwencjonowania, który polega na generowaniu sekwencji kandydujących, a następnie obliczaniu wsparcia tych sekwencji kandydujących, w przypadku algorytmu PrefixSpan wzorce sekwencji czy tez sekwencje kandydujące są konstruowane iteracyjnie.
Uogólnione sformułowanie problemu

Oryginalne sformułowanie problemu odkrywania wzorców sekwencji, sformułowane przez Agrawala i Srikanta, abstrahowało od ograniczeń czasowych odnośnie rozpiętości czasowej analizowanych wzorców sekwencji czy też odstępów czasowych pomiędzy kolejnymi zdarzeniami wchodzącymi w skład wzorców sekwencji. Jak już wspominaliśmy, celem odkrywania wzorców sekwencji jest znalezienie typowej, często powtarzającej się, sekwencji zachodzenia pewnych zdarzeń. Oczywiście, wzorzec sekwencji nie implikuje przyczynowości pomiędzy zdarzeniami wchodzącymi w skład wzorca - wzorzec sekwencji opisuje jedynie, i to w przybliżeniu, statystyczne prawdopodobieństwo wystąpienia określonych zdarzeń w kolejności określonej przez wzorzec sekwencji. Niemniej, pewna zależność lub współwystępowanie, często trudne do udowodnienia, prawdopodobnie występuje pomiędzy zdarzeniami wchodzącymi w skład wzorca, lub przynajmniej, użytkownik\dbiorca systemu eksploracji danych często tak postrzega wzorzec sekwencji. Wracając do przykładu wzorca sekwencji, który przytoczyliśmy na początku wykładu o kliencie wypożyczającym film pod tytułem Gwiezdne wojny, w ciągu tygodnia wypożyczy film pod tytułem Imperium kontratakuje, a następnie, w ciągu kolejnego tygodnia, wypożyczy film po tytułem Powrót Jedi.
Zauważmy, że wzorzec ten dla właściciela wypożyczalni ma znaczenie, tylko wówczas jeżeli horyzont czasowy tego wzorca jest określony w czasie. Z faktu, że ktoś wypożyczył określony film nie wynika, że musi z bliżej nieznanych powodów wypożyczyć inny film. Niemniej, w przypadku przytoczonego wzorca sekwencji istnieje jego racjonalne wytłumaczenie: osoby, które obejrzały film ‘Gwiezdne Wojny’ i którym film ten im się spodobał, najprawdopodobniej będą zainteresowane śledzeniem dalszych losów bohaterów filmu. Co więcej te osoby lubią również ten gatunek filmu reprezentowany przez trylogię Gwiezdne Wojny, Imperium Kontratakuje i Powrót Jedi. Ponadto osoby te starają się wypożyczyć wspomniane filmy, dopóki pamiętają jeszcze fabułę poszczególnych filmów trylogii. Z drugiej strony, trudno uznać za wzorzec sekwencji wypożyczenie filmu Gwiezdne Wojna a później Imperium Kontratakuje w odstępie kilku lat. W związku z tym, widzimy że dotychczasowe przedstawienie problemu nie uwzględnia ograniczeń czasowych na wzorce sekwencji. Przedstawimy obecnie uogólnione sformułowanie problemu odkrywania wzorców sekwencji, w którym uwzględnia się ograniczenia czasowe na wzorce sekwencji. Zanim przejdziemy do uogólnionego sformułowania problemu, wprowadzimy kilka nowych pojęć.
Sekwencją S nazywać będziemy uporządkowaną listę wyrazów (T1, T2, ..., Tn), gdzie Ti jest zbiorem elementów.
Z każdym wyrazem sekwencji Ti sekwencji S jest związany znacznik czasowy ts(Ti), określający czas wystąpienia zdarzenia Ti.
Wyrazy Ti w sekwencji S są uporządkowane według rosnących wartości ich znaczników czasowych.

W dalszej części będziemy stosowali zamiennie następującą notację na oznaczenie sekwencji <T1, T2, …, Tn> lub, gdy konieczne będzie explicite wskazanie znaczników czasowych wyrazów sekwencji, < (T1): ts(T1) , (T2): ts(T2) , ..., (Tn): (ts(Tn)) >. Wprowadzimy nowe pojęcia związane z ograniczeniami czasowymi:
Oknem zdarzeń (w-size) będziemy nazywać przedział czasu, w ramach którego zbiór transakcji w bazie danych D jest interpretowany jako „pojedyncza” transakcja.
Minimalny odstęp (min-gap ) to minimalny odstęp czasowy pomiędzy kolejnymi wyrazami wzorca sekwencji.
Maksymalny odstęp (max-gap ) to maksymalny odstęp czasowy pomiędzy kolejnymi wyrazami wzorca sekwencji.
Wartości wszystkich ograniczeń czasowych są definiowane przez użytkownika.
Sformułowanie problemu

Problem odkrywania wzorców sekwencji z ograniczeniami czasowymi możemy sformułować w następujący sposób. Dana jest baza danych sekwencji DS ze znacznikami czasowymi. Celem procesu odkrywania wzorców sekwencji z ograniczeniami czasowymi jest znalezienie wszystkich sekwencji, których wsparcie w bazie danych sekwencji DS przekracza pewną zadaną wartość minimalną, oznaczoną minsup. Sekwencje, które spełniają powyższy warunek minimalnego wsparcia, nazywamy
sekwencjami częstymi lub
wzorcami sekwencji . Analogicznie, sekwencje częste, które są maksymalne, nazywać będziemy
maksymalnymi wzorcami sekwencji.
Problem

Zasadniczy problem związany z konstrukcją algorytmów odkrywania wzorców sekwencji w obecności ograniczeń czasowych wiąże się z problemem własności monotoniczności miary wsparca. Własność monotoniczności miary wsparcia, w kontekście definicji zawierania się sekwencji w obecności ograniczeń czasowych, musi być zdefiniowana w nieco inny sposób. Wynika to z następującego spostrzeżenia. W przypadku braku ograniczenia {max-gap}, można łatwo pokazać, że dowolna sekwencja X, zawierająca sekwencję S, zawiera również wszystkie podsekwencje Y sekwencji S; Y całkowicie zawiera się w S. W przypadku obecności ograniczenia czasowego {max-gap}, powyższe stwierdzenie nie jest prawdziwe.
Przykładowo:
Zakładamy, że maksymalna odstęp max-gap będzie równy 3. Dana jest sekwencja X = <(1 2): 1, (3 4): 3, (5 6): 5, (7 8): 7>.
X zawiera sekwencję S = <(1 2): 1, (3 4): 3, (5 6): 5>, ale X nie zawiera sekwencji Y = <(1 2): 1, (5 6): 5>, która jest podsekwencją sekwencji S.
Odległość pomiędzy dwoma wyrazami przekracza maksymalny odstęp.

W konsekwencji wcześniejszych spostrzeżeń, możemy podsumować, że brak własności monotoniczności miary wsparcia w przypadku ograniczenia max-gap. Brak monotoniczności uniemożliwia generowanie sekwencji kandydujących w oparciu o ideę algorytmu Apriori – ograniczenie przestrzeni możliwych rozwiązań (inaczej mówiąc, ograniczenie przestrzeni generacji potencjalnie częstych sekwencji kandydujących). Rozwiązaniem problemu jest wprowadzenie pojęcia podsekwencji spójnej (ang. contiguous subsequence).

Sekwencję Y nazywamy
podsekwencją spójną sekwencji X, wtedy i tylko wtedy, gdy spełniony jest jeden z następujących warunków:
-
sekwencja Y powstała z sekwencji X poprzez usunięcie pojedynczego elementu z pierwszego lub ostatniego wyrazu sekwencji X,
-
sekwencja Y powstała z sekwencji X poprzez usunięcie pojedynczego elementu z dowolnego wyrazu sekwencji X, pod warunkiem, że wyraz ten zawierał co najmniej dwa elementy,
-
sekwencja Y jest podsekwencją spójną sekwencji Z, która, z kolei, jest podsekwencją spójną sekwencji X.

Własność monotoniczności miary wsparcia sekwencji można sformułować, korzystając z pojęcia podsekwencji spójnej, następująco: dowolna sekwencja X, zawierająca sekwencję S, zawiera również wszystkie podsekwencje spójne sekwencji S. Innymi słowy, wsparcie sekwencji X nie jest nigdy większe od wsparcia jakiejkolwiek podsekwencji spójnej sekwencji X. Jeżeli zatem sekwencja X jest sekwencją częstą, to wszystkie jej podsekwencje spójne muszą być częste. Własność tę można wykorzystać do ograniczenia przestrzeni poszukiwań wzorców sekwencji. Do znajdowania wzorców sekwencji z ograniczeniami można wykorzystać algorytm GSP (algorytm typu Apriori-like – zmodyfikowana wersja algorytmu podstawowego przedstawioną na poprzednim wykładzie).
Uogólnione wzorce sekwencji

Podobnie jak w przypadku reguł asocjacyjnych, tak i w odniesieniu do wzorców sekwencji, użytkownicy są często zainteresowani znajdowaniem wzorców sekwencji, które uwzględniają taksonomie elementów. Zainteresowanie znajdowaniem wzorców sekwencji może być związanie z pewnymi dodatkowymi ograniczeniami. Mogą to być ograniczenia elementów np. ‘Znajdź wszystkie produkty, które klienci kupują najczęściej zanim kupią DVD’, lub też ograniczenia czasowe ‘Znajdź wszystkie produkty, które klienci kupują w ciągu miesiąca od dnia zakupu telewizora’.

Wzorce sekwencji, których wyrazy, poza elementami, zawierają również nazwane grupy elementów nazywamy
uogólnionymi wzorcami sekwencji . Analogicznie jak w przypadku reguł asocjacyjnych w odniesieniu do wzorców sekwencji możemy rozpatrywać je w kategorii wymiarowości. Wielowymiarowymi (ilościowymi) wzorcami sekwencji nazywamy wzorce sekwencyjne określające zależności kolejnościowe pomiędzy zdarzeniami opisanymi zarówno atrybutami kategorycznymi jak i atrybutami ciągłymi.
Podstawowy algorytm odkrywania uogólnionych wzorców sekwencji jest oparty na idei podstawowego algorytmu odkrywania wielopoziomowych reguł asocjacyjnych Podobnie jak w podstawowym algorytmie odkrywania wielopoziomowych reguł asocjacyjnych, dla każdej sekwencji s należącej do DS, rozszerzamy każdy wyraz si sekwencji s o zbiór wszystkich poprzedników (nazwane grupy elementów) każdego elementu należącego do tego wyrazu. Pomijamy w tym rozszerzeniu korzeń taksonomii, oraz, ewentualnie, usuwamy z każdego wyrazu powtarzające się elementy. W konsekwencji tej transformacji otrzymujemy zbiór tak zwanych „rozszerzonych sekwencji”. Następnie, w odniesieniu do bazy danych rozszerzonych sekwencji możemy zastosować dowolny algorytm odkrywania wzorców sekwencji (Apriori lub PrefixSpan).






























