Indeksy
Plan wykładu

Celem wykładu jest omówienie podstawowych koncepcji indeksowania danych i struktur indeksowych. W ramach wykładu zostaną omówione:
- wprowadzenie do problematyki indeksowania danych,
- charakterystyka różnego rodzaju indeksów (podstawowy, zgrupowany, wtórny, rzadki i gęsty),
- indeks wielopoziomowy statyczny (ISAM),
- indeks wielopoziomowy dynamiczny (B+-drzewo),
- algorytm wstawiania danych do indeksu B+-drzewo.
Wprowadzenie
Rozważmy plik zawierający uporządkowane lub nieuporządkowane rekordy danych. Jak pamiętamy z poprzedniego wykładu wyszukiwanie danych w plikach nie jest efektywne. Z tego względu chcielibyśmy znaleźć sposób efektywnego wyszukiwania danych.

Rozwiązanie tego problemu bazuje na wykorzystaniu drugiego pliku zdefiniowanego na atrybucie wykorzystanym do specyfikowania kryterium przeszukiwania. Plik ten zawierałby rekordy odpowiadające poszukiwanym wartościom pierwszych rekordów w poszczególnych blokach pliku danych. Rekordy w dodatkowym pliku miałyby postać: <pierwszy klucz w bloku, wskaźnik do bloku>, a plik dodatkowy byłby uporządkowany według wartości poszukiwanych.
Taki plik dodatkowy nazywa się indeksem.
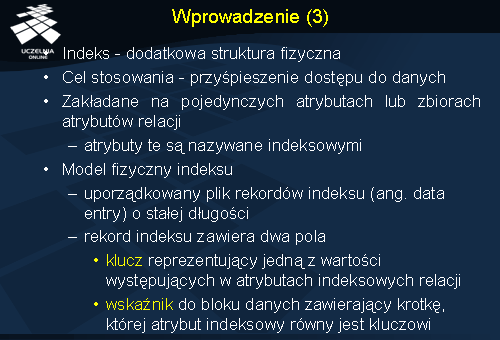
Indeks zdefiniowany na pliku jest dodatkową strukturą fizyczną, której celem jest przyspieszenie wykonywania operacji, które nie są wystarczająco efektywnie wspierane przez podstawowe organizacje plików i struktury logiczne danych.
Indeksy są zakładane na pojedynczych atrybutach lub zbiorach atrybutów relacji. Atrybuty te noszą nazwę atrybutów indeksowych.
Indeks jest uporządkowanym plikiem rekordów indeksu (ang. data entry) o stałej długości. Rekordy indeksu zawierają dwa pola: klucz reprezentujący jedną z wartości występujących w atrybutach indeksowych relacji oraz wskaźnik do bloku danych zawierający krotkę, której atrybut indeksowy równy jest kluczowi.

Każdy rekord indeksu, oznaczony k*, zawiera dostateczną informację umożliwiającą wyszukanie (jednego lub więcej) rekordów danych o wartości klucza k.
Projektując strukturę indeksu należy odpowiedzieć na dwa pytania:
Po pierwsze, w jaki sposób rekordy indeksu powinny być zorganizowane, aby efektywnie wspierać wyszukiwanie rekordów o danej wartości klucza? Po drugie, co powinien zawierać rekord indeksu?
Rekordy indeksu

Rekord indeksu k* umożliwia wyszukanie rekordów danych o wartości klucza k.
Wyróżnia się cztery typy rekordów indeksu:
1. Rekord indeksu k* jest rekordem danych (o wartości klucza k).
2. Rekord indeksu jest parą <k, rid>, gdzie rid jest identyfikatorem rekordu danych o wartości klucza k.
3. Rekord indeksu jest parą <k, rid-list>, gdzie rid-list jest listą identyfikatorów rekordów danych o wartości klucza k.
4. Rekord indeksu jest parą <k, bitmapa>, gdzie bitmapa jest wektorem 0 i 1 reprezentującym zbiór rekordów danych.
Rodzaje indeksów - charakterystyka atrybutu indeksowego

Z punktu widzenia charakterystyki atrybutu indeksowego wyróżnia się trzy rodzaje indeksów:
- indeks podstawowy (ang. primary index)
- indeks zgrupowany (ang. clustering index)
- indeks wtórny (ang. secondary index).
Indeks podstawowy jest założony na atrybucie porządkującym indeksowanego pliku. Atrybut porządkujący określa porządek rekordów w
pliku. Dla indeksu podstawowego atrybut porządkujący przyjmuje wartości unikalne.
Indeks zgrupowany jest zakładany również na atrybucie porządkującym, ale w tym przypadku jego wartości nie są unikalne.
Indeks wtórny jest zakładany na atrybucie, który nie jest atrybutem porządkującym pliku.
Rodzaje indeksów - wskazania do pliku danych

Z punktu widzenia liczby wskazań indeksu do pliku danych wyróżnia się indeksy gęste (ang. dense) i indeksy rzadkie (ang. sparse). Indeks gęsty posiada rekord indeksu dla każdego rekordu indeksowanego pliku danych. Indeks rzadki posiada rekordy tylko dla wybranych rekordów indeksowanego pliku danych.
Rodzaje indeksów - liczba poziomów

Z punktu widzenia liczby poziomów indeksu wyróżnia się indeksy jednopoziomowe i wielopoziomowe. W pierwszym przypadku, dla pliku danych jest tworzony tylko jeden indeks (plik indeksu). W drugim przypadku, dla pliku danych tworzy się indeks (jak w przypadku pierwszym). Dodatkowo, do indeksu tworzy się dodatkowy indeks.
Indeks podstawowy

Indeks podstawowy jest indeksem rzadkim ponieważ nie wszystkie rekordy pliku danych posiadają rekordy indeksowe. Rekord indeksowy indeksu podstawowego dla wartości X zawiera adres bloku danych, w którym znajduje się rekord danych z wartością atrybutu indeksowego równą X.
Poglądową strukturę indeksu podstawowego przedstawia slajd. Jak widać, wskazania z rekordów indeksowych prowadzą do bloków danych.
Indeks zgrupowany
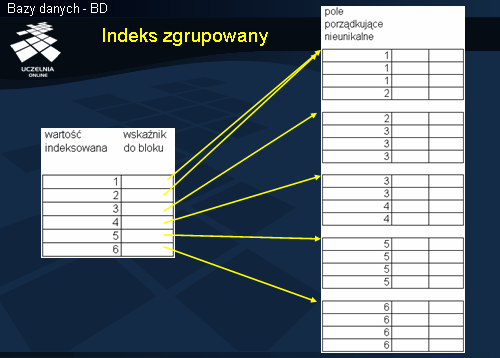
Indeks zgrupowany jest również indeksem rzadkim ponieważ nie wszystkie rekordy pliku danych posiadają rekordy indeksowe. Rekord indeksowy indeksu zgrupowanego dla wartości X zawiera adres bloku danych, w którym znajduje się pierwszy rekord danych z wartością atrybutu indeksowego równą X. Widać to wyraźnie dla wartości 2 rekordu indeksu. Rekord ten posiada wskazanie do pierwszego bloku danych - w bloku tym znajduje się pierwszy rekord z wartością 2 indeksowanego atrybutu.
Taka organizacja pliku powoduje problemy z wstawianiem i rekordów, ponieważ porządek rekordów po wstawieniu musi pozostać zachowany.
Indeks zgrupowany z blokami nadmiarowymi

Rozwiązaniem tego problemu jest po pierwsze, zarezerwowanie całego bloku na rekordy z tą samą (jedną) wartością. Po drugie, zastosowanie bloków nadmiarowych, jak pokazuje slajd. Wstawiane rekordy są umieszczane w wolnych szczelinach bloku głównego, a po jego zapełnieniu - w odpowiednim bloku nadmiarowym, do którego prowadzi wskaźnik z bloku głównego.
W przykładzie ze slajdu, rekord z wartością 3 nie mieści się w bloku głównym, więc jest składowany w bloku nadmiarowym. Z bloku głównego przechowującego rekordy z wartością atrybutu indeksowego równą 3 prowadzi wskaźnik do bloku nadmiarowego.
Indeks wtórny

Indeks wtórny jest również uporządkowany. Jest on zakładany na atrybucie indeksowym pliku danych, który nie jest atrybutem porządkującym tego pliku. Każdy rekord pliku danych posiada swój odpowiednik w rekordzie indeksu. Stąd, indeks wtórny jest indeksem gęstym.
Rekord indeksu wtórnego składa się z dwóch pól: wartości pola indeksowego i wskaźnika albo do rekordu albo do bloku danych zawierającego ten rekord.
Na slajdzie przedstawiono gęsty indeks wtórny założony na polu nieporządkującym, którego wartości są unikalne. Rekordy indeksu posiadają wskaźniki do bloków danych.
Indeks o kluczu złożonym

Klucz indeksu może zawierać kilka atrybutów – taki klucz nazywamy kluczem złożonym. W przykładzie ze slajdu zdefiniowano cztery różne indeksy. Pierwszy na kluczu złożonym <wiek, pensja>, drugi na kluczu złożonym <pensja, wiek>, trzeci na kluczu <wiek>, a czwarty na kluczu <pensja>.
Indeksy na kluczach złożonych stosuje się do wyszukiwania rekordów spełniających warunki równościowe (tzw. zapytania punktowe) nałożone jednocześnie na pola występujące w kluczu złożonym.
Indeks <wiek, pensja> będzie przydatny do wyszukiwania rekordów spełniających warunki równościowe nałożone jednocześnie na pole wiek i na pole pensja. Może też zostać wykorzystany przy warunkach nałożonych na inne pola, razem z warunkami nałożonymi na wiek i pensję. Ponadto, indeks <wiek, pensja> może zostać wykorzystany do wyszukiwania rekordów z warunkiem nałożonym tylko na pole wiek.
Indeks ten będzie jednak nieprzydatny do poszukiwania rekordów z warunkami nałożonymi na atrybut pensja, ponieważ atrybutem wiodącym tego indeksu jest wiek. W takim przypadku, mógłby zostać wykorzystany indeks <pensja, wiek>.
Z tych powodów, bardziej uniwersalne są indeksy zakładane na pojedynczych atrybutach. Są one jednak mniej efektywne od indeksów złożonych w przypadku warunków poszukiwania jednocześnie nałożonych na indeksowane atrybuty.
Indeks wielopoziomowy - ISAM

Wyszukanie danych z wykorzystaniem indeksu jednopoziomowego wymaga przeszukania pliku indeksu. Z wykorzystaniem znalezionych rekordów indeksu następuje odczytanie rekordów danych. Należy zwrócić uwagę na fakt, że plik indeksu jest przeszukiwany algorytmem połowienia binarnego ponieważ jest to plik uporządkowany. Algorytm ten nie należy do efektywnych. Z tego względu wprowadzono indeksy wielopoziomowe, których efektywność przeszukiwania jest większa.
Jedną z fundamentalnych koncepcji indeksu wielopoziomowego jest struktura ISAM (ang. Indexed Sequential Access Method), oryginalnie opracowana przez IBM. Koncepcyjnie struktura ta jest zbudowana z dwóch poziomów. Poziom pierwszy indeksuje cylindry. Rekordy indeksu na tym poziomie zawierają pary wartości: poszukiwany klucz i adres do indeksu ścieżki dyskowej. Poziom drugi indeksuje ścieżki. Jego rekordy zawierają pary wartości: poszukiwany klucz i adres ścieżki. Jak widać, jest to struktura silnie związana z zastosowanym sprzętem komputerowym.
Rozwinięciem struktury ISAM jest VSAM (ang. Virtual Sequential Access Method). VSAM jest już niezależna od rozwiązań sprzętowych.
Indeks wielopoziomowy - koncepcja ogólna
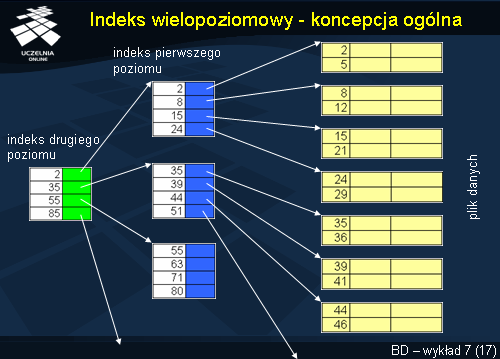
Ogólną koncepcję indeksu wielopoziomowego przedstawiono na slajdzie. Indeks na pierwszym poziomie adresuje bloki danych. Każdy rekord tego indeksu zawiera wartość pola indeksowego i adres bloku danych, w którym ta wartość się znajduje. Rekordy tego indeksu są przechowywane w pliku uporządkowanym zgodnie z wartościami klucza indeksu pierwszego poziomu. Rekordy indeksu drugiego poziomu zawierają adresy bloków indeksu pierwszego poziomu.
ISAM

ISAM jest indeksem statycznym, co oznacza, że nie posiada zaawansowanych mechanizmów modyfikowania struktury w sytuacji zmodyfikowania zawartości indeksowanego pliku (dodanie, zmodyfikowanie, usunięcie rekordu). Usunięcie rekordu powoduje powstanie pustego miejsca w bloku indeksu. Nowe rekordy są dodawane do bloków przepełnienia. W konsekwencji struktura indeksu typu ISAM staje się nieefektywna.
Rozwiązaniem tego problemu jest wprowadzenie indeksów dynamicznych. Najpowszechniej stosowanymi indeksami dynamicznymi są indeksy drzewiaste, S-drzewa, B-drzewa, B+-drzewa.
Struktura drzewiasta
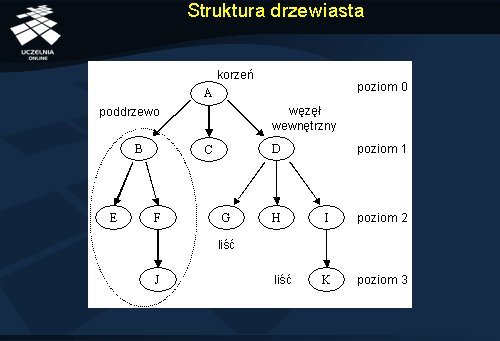
Na slajdzie przedstawiono ogólną strukturę drzewiastą. Wyróżnia się w niej tzw. korzeń, będący wierzchołkiem (punktem wejścia) całej struktury. Na slajdzie korzeniem jest węzeł A. Z korzenia prowadzą łuki, czyli wskazania albo do węzłów wewnętrznych (węzły B i D na rysunku) albo do liści (węzeł C). Węzeł wewnętrzny posiada wskazania do innych węzłów. Liść nie posiada wskazań do innych węzłów. Jest więc elementem końcowym całej struktury. Przykładowy indeks ze slajdu składa się z 4 poziomów. Przy czym korzeń znajduje się na poziomie 0.
Indeks B+-drzewo

Najpowszechniej stosowanym drzewiastym indeksem dynamicznym jest B+-drzewo. Jest on implementowany we wszystkich komercyjnych i niekomercyjnych SZBD. Ponadto stanowi podstawę implementacji innych indeksów, tj. indeksów bitmapowych i połączeniowych.
Indeks B+-drzewo jest zrównoważoną strukturą drzewiastą, w której wierzchołki wewnętrzne służą do wspomagania wyszukiwania, natomiast wierzchołki liści zawierają rekordy indeksu ze wskaźnikami do rekordów w plikach danych. Zrównoważenie struktury oznacza, że odległość (liczba poziomów) od korzenia do dowolnego liścia jest zawsze taka sama.
W celu zapewnienia odpowiedniej efektywności realizacji zapytań przedziałowych wierzchołki liści stanowią listę dwukierunkową.
Indeks B+-drzewo - charakterystyka

Najważniejsza charakterystyka indeksu B+-drzewo jest następująca:
Po pierwsze, operacje wstawiania i usuwania rekordów indeksu pozostawiają indeks zrównoważonym.
Po drugie, każdy wierzchołek jest wypełniony w co najmniej 50% (za wyjątkiem korzenia). Odstępstwo od tej reguły może być spowodowane operacjami usuwania rekordów. Dla operacji usuwania, rekord indeksu jest usuwany z indeksu ale wolne miejsce pozostaje w liściu. W konsekwencji, wierzchołki liści mogą być wypełnione w mniej niż 50%.
Po trzecie, wyszukanie rekordu wymaga przejścia od korzenia do liścia. Długość ścieżki od korzenia do dowolnego liścia nazywamy wysokością drzewa indeksu.
Po czwarte, jak wspomniano, B+-drzewo jest indeksem zrównoważonym.
Struktura indeksu B+ drzewa
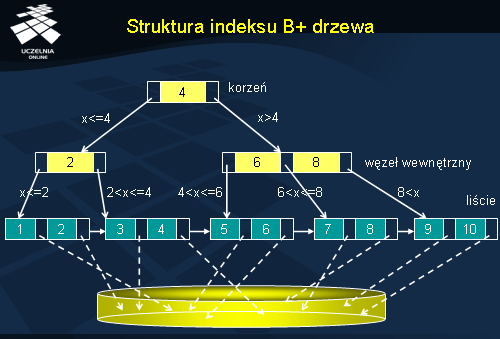
Przykładowy indeks B+-drzewo przedstawiono na slajdzie. Składa się on z trzech poziomów: korzenia, węzłów wewnętrznych i liści. W korzeniu jest przechowywana pewna wartość graniczna klucza indeksu i wskaźniki do węzłów wewnętrznych. W naszym przykładzie wartością graniczną jest 4, a korzeń zawiera wskaźniki do dwóch węzłów wewnętrznych. W węzłach wewnętrznych są przechowywane również pewne wartości graniczne klucza indeksu i wskaźniki do liści. Liście z kolei przechowują pary: <wartość klucza indeksu, wskaźnik do rekordu na dysku>.
Węzeł wewnętrzny

Struktura węzła wewnętrznego indeksu B+-drzewo rzędu p jest następująca.
1. Węzeł wewnętrzny ma następującą postać: wskaźnik do węzła, wartość klucza indeksu, kolejny wskaźnik, kolejna wartość, itd. Liczba wskaźników jest o jeden większa od liczby wartości klucza.
<P1, K1, P2, ..., PQ-1, KQ-1, PQ>
gdzie Q <= p; Pi jest wskaźnikiem do poddrzewa; Ki jest wartością klucza indeksu.
Maksymalna liczba wskaźników jaka może zostać zapisana w węźle jest nazywana rzędem B+-drzewa i jest oznaczana jako p.
2. Dla każdego wierzchołka wewnętrznego zachodzi:
K1 < K2 < ... < KQ-1
Oznacza to, że wartości klucza indeksowego są uporządkowane (od lewej - wartości najmniejsze do prawej - wartości największe).
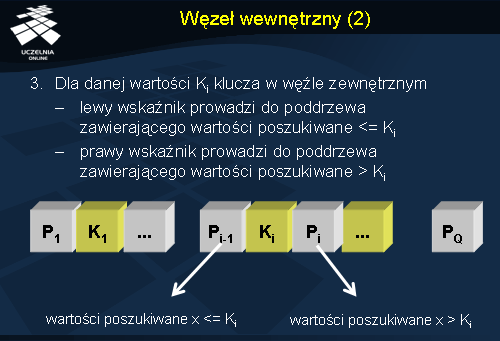
3. Dla danej wartości Ki klucza w węźle wewnętrznym, lewy wskaźnik prowadzi do poddrzewa zawierającego wartości poszukiwane <= Ki, a prawy wskaźnik prowadzi do poddrzewa zawierającego wartości poszukiwane > Ki, jak pokazano na slajdzie.

4. Każdy wierzchołek wewnętrzny posiada co najwyżej p wskaźników do poddrzew.
5. Dla każdego wierzchołka wewnętrznego liczba wskaźników do poddrzew jest określona jako najmniejsza liczba całkowita większa lub równa połowie rzędu drzewa. Korzeń posiada co najmniej 2 wskaźniki do poddrzew.
6. Każdy wierzchołek wewnętrzny o Q wskaźnikach posiada Q-1 wartości kluczy.
Wierzchołek wewnętrzny
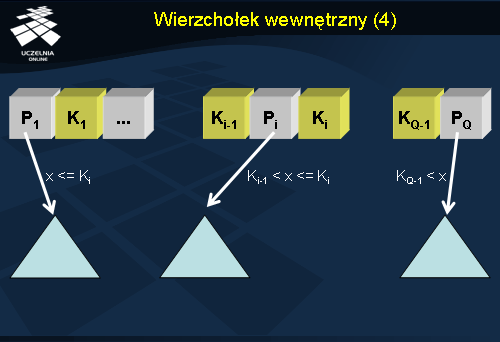
Podsumowanie struktury wierzchołka wewnętrznego przedstawiono na slajdzie.
Liść
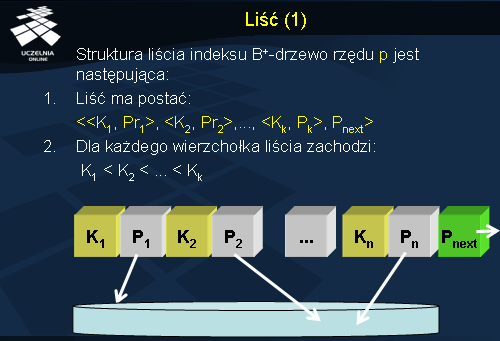
Struktura liścia indeksu B+-drzewo rzędu p jest następująca:
1. Liść ma postać:
- zbiór par: wartość klucza indeksu, wskaźnik do rekordu (bloku danych) z tą wartością klucza (oznaczone jako Kk, Pk)
<K1, P1>, <K2, P2>,..., <Kk, Pk>, Pnext>
K1, K2, ..., Kk są wartościami klucza indeksu;
P1, P2, ..., Pk są wskaźnikami do rekordów na dysku lub do bloków danych;
- wskaźnik do następnego liścia.
W indeksach typu B*-drzewo, każdy liść ma dodatkowo wskaźnik do poprzedniego liścia.
2. Dla każdego wierzchołka liścia zachodzi:
K1 < K2 < ... < KQ-1
Oznacza to, że wartości klucza indeksowego są uporządkowane (od lewej - wartości najmniejsze do prawej - wartości największe).

3. Dla każdego liścia minimalna liczba wartości kluczy indeksu jest określona jako największa liczba całkowita mniejsza lub równa połowie rzędu drzewa.
4. Wszystkie liście znajdują się na tym samym poziomie (tej samej wysokości).
Obliczanie rzędu indeksu

Przedstawiony zostanie teraz tok rozumowania prowadzący do obliczenia rzędu indeksu. Przypominamy, że rząd indeksu oznaczamy jako p.
Przyjmijmy, że: V oznacza rozmiar klucza indeksu; P oznacza rozmiar wskaźnika do bloku; B oznacza rozmiar bloku danych (dyskowego); r oznacza liczbę indeksowanych rekordów w pliku danych; b oznacza liczbę bloków pliku danych.
Pamiętamy, że węzły wewnętrzne zawierają maksymalnie p wskaźników i p-1 kluczy. Ponieważ każdy węzeł musi się zmieścić w pojedynczym bloku dyskowym, więc rząd B+-drzewa jest największą liczbą całkowitą spełniającą nierówność ze slajdu (oznaczoną symbolem 1).
Z innych przydatnych wzorów wymienić należy wzory obliczające minimalną wysokość indeksu rzadkiego (wzór 2) i minimalną wysokość indeksu gęstego (wzór 3), przedstawione na slajdzie.
Obliczanie rzędu indeksu - przykład

Rozważmy następujący przykład ilustrujący sposób obliczania rzędu B+-drzewa.
Niech: liczba indeksowanych rekordów danych wynosi r=30 000, rozmiar bloku wynosi B=1kB, rozmiar rekordu wynosi R=100B, rozmiar klucza indeksu wynosi V=9B i rozmiar wskaźnika wynosi P=6B.
Przyjmujemy ponadto, że rekordy mają stałą długość i nie są dzielone między bloki. Na pliku danych jest zakładany indeks wtórny.
Ponieważ rekordy mają stałą długość i nie są dzielone między bloki, liczbę rekordów w bloku obliczymy za pomocą wzoru 1.
Liczbę bloków danych do składowania 30000 rekordów obliczymy za pomocą wzoru 2.

Rząd węzła obliczamy przekształcając wzór 3 ze slajdu do wzoru 4. Po podstawieniu wartości do wzoru 4 otrzymujemy wynik: rząd węzła wewnętrznego p=68. Z wykorzystaniem obliczonej wartości rzędu węzła możemy następnie obliczyć minimalną wysokość indeksu niezbędną do poindeksowania 30000 rekordów danych. Wykorzystujemy do tego celu wzór 5. Po podstawieniu danych, otrzymujemy wynik - indeks musi mieć przynajmniej 3 poziomy.
Przykład

Jak łatwo dowieźć analitycznie, indeks B+-drzewo znakomicie przyspiesza wyszukiwanie rekordu z pliku, w porównaniu z dostępem do pliku bez indeksu. Jeżeli w pliku jest wyszukiwany rekord z kryterium nałożonym na atrybut nieporządkujący, wówczas należy przeszukać cały plik. Średnio będzie to wymagało odczytania połowy bloków przechowujących rekordy danych, czyli w naszym przykładzie 1500.
W przypadku indeksu B+-drzewo należy znaleźć odpowiedni liść i sięgnąć po rekord do dysku. Znalezienie liścia wymaga odczytania 3 bloków indeksu - korzenia, węzła wewnętrznego i liścia. Korzystając ze wskaźnika w liściu, należy odczytać jeden blok danych zawierający poszukiwany rekord. Znalezienie rekordu będzie więc wymagało 4 dostępów do dysku.
Wstawianie danych do indeksu - przykład
Zarządzanie strukturą indeksu B+-drzewo w sytuacjach wstawiania, usuwania i modyfikowania wartości atrybutu indeksowego rekordów danych jest realizowane za pomocą specjalizowanych algorytmów. Na kilku kolejnych slajdach przedstawimy ideę działania algorytmu modyfikowania struktury indeksu na skutek wstawiania rekordów danych.
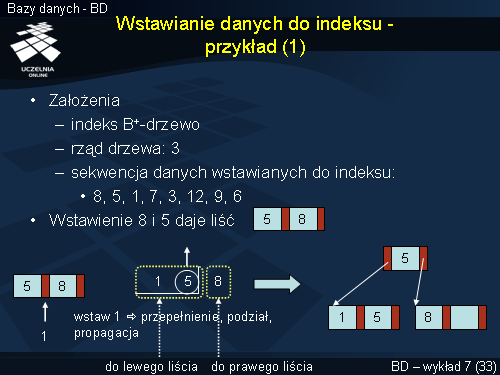
Dla uproszczenia przyjmijmy, że indeks jest rzędu 3. Oznacza to, że każdy węzeł posiada minimalnie 2 i maksymalnie 3 wskaźniki. Liść posiada od 1 do dwóch wartości atrybutu indeksowego. Do indeksu są wstawiane następujące wartości w kolejności ich wymienienia: 8, 5, 1, 7, 3, 12, 9 ,6.
Wstawione wartości 8 i 5 mieszczą się w jednym bloku indeksu, więc wystarczy je przechować jako liść.
Wstawienie wartości 1 do węzła spowodowałoby jego przepełnienie. Z tego powodu węzeł jest rozbijany na 2. W tym celu porządkujemy wartości istniejące w węźle i wartość wstawianą, od lewej (najmniejsza) do prawej (największa). Wartość środkową, czyli 5, przenosimy do poziomu wyższego - staje się ona wartością w korzeniu. Wartości 1 i 5 trafiają do lewego liścia, a 8 - do prawego, jak pokazano na slajdzie.
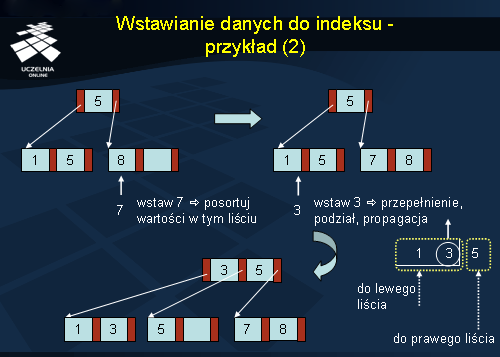
Wartość 7 musi być wstawiona do prawego liścia, który posiada miejsce na jedną wartość. Wartości w tym liściu należy posortować.
Wartość 3 musi być wstawiona do lewego liścia. Jednak jest on już w całości zajęty. Z tego powodu węzeł jest rozbijany na 2. W tym celu porządkujemy wartości istniejące w węźle i wartość wstawianą, od lewej (najmniejsza) do prawej (największa). Wartość środkową, czyli 3, przenosimy do korzenia. Wartości 1 i 3 trafiają do lewego liścia, a 5 - do prawego, jak pokazano na slajdzie.
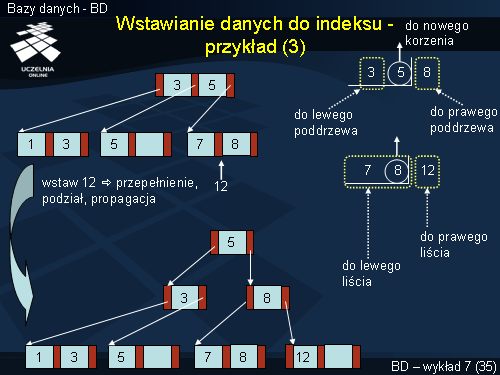
Wartość 12 musi być wstawiona do skrajnie prawego liścia. Jednak jest on już w całości zajęty. Z tego powodu węzeł jest rozbijany na 2. W tym celu porządkujemy wartości istniejące w węźle i wartość wstawianą, od lewej (najmniejsza) do prawej (największa). Wartość środkową, czyli 8, przenosimy do korzenia. Wartości 7 i 8 trafiają do lewego liścia, a 12 - do prawego, jak pokazano na slajdzie.
Ponadto, w tym przypadku wartość 8 powinna trafić do korzenia, który jest już w całości wypełniony. Z tego względu ulega on rozbiciu na nowy korzeń i dwa węzły wewnętrzne. W tym celu porządkujemy wartości już przechowywane w korzeniu i wstawianą do niego wartość, jak pokazano na slajdzie. Wartość środkowa, czyli 5 trafia do nowego korzenia. Wartość 3 trafia do lewego poddrzewa, a wartość 8 - do prawego, jak pokazano na slajdzie.
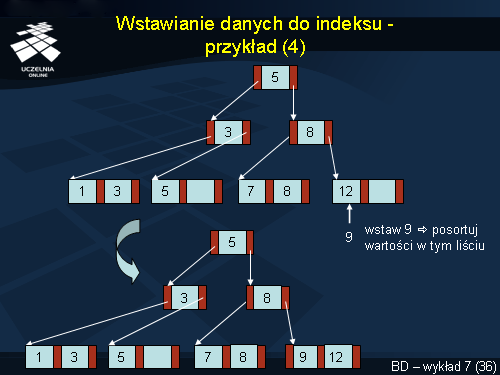
Wartość 9 musi być wstawiona do skrajnie prawego liścia, który posiada miejsce na jedną wartość. Wartości w tym liściu należy posortować.
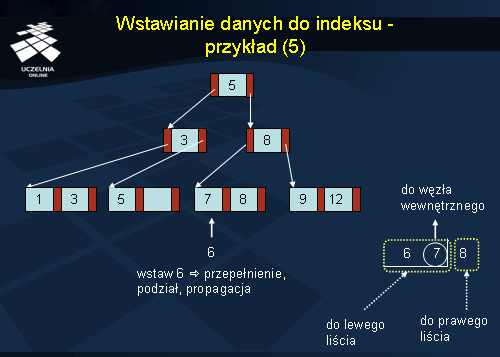
Wartość 6 musi być wstawiona do trzeciego od lewej liścia. Jednak jest on już w całości zajęty. Z tego powodu węzeł jest rozbijany na 2. W tym celu porządkujemy wartości istniejące w węźle i wartość wstawianą, od lewej (najmniejsza) do prawej (największa). Wartość środkową, czyli 7, przenosimy do węzła wewnętrznego. Wartości 6 i 7 trafiają do lewego liścia, a 8 - do prawego, jak pokazano na slajdzie.
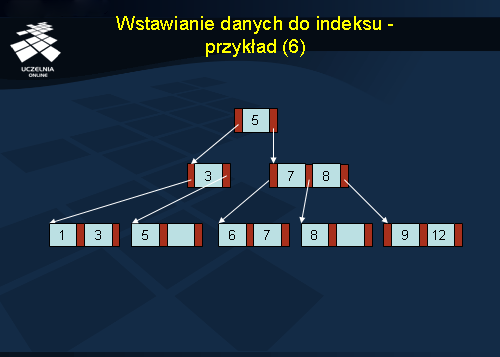
Ostateczna struktura indeksu została przedstawiona na slajdzie.




































