W dalszej części wykładu skoncentrujemy się na metodach klasyfikacji. W literaturze zaproponowano wiele modeli klasyfikacji, są to np.: drzewa decyzyjne, tabele decyzyjne, metoda Bayesa, sieci neuronowe, algorytmy genetyczne, metoda k-najbliższych sąsiadów (ang. k-nearest neighbor ), zbiory przybliżone i wiele innych statystycznych metod, które można zastosować przy klasyfikacji danych. Różnorodność modeli spowodowała wyspecyfikowanie kryteriów porównawczych metod, dzięki którym można dokonać odpowiedniego wyboru metody dla danego zastosowania. Istnieje szereg kryteriów porównawczych, które obecnie krótko scharakteryzujemy. Pierwszym kryterium porównawczym jest kryterium dokładności predykcji (ang. 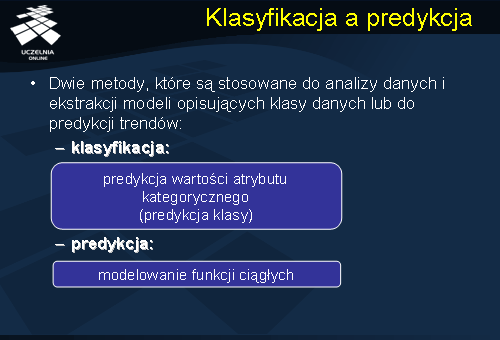predictive accuracy ). Pod pojęciem predykcji rozumiemy zdolność modelu do poprawnej predykcji wartości atrybutu decyzyjnego (klasy) nowego przykładu. Innym kryterium jest kryterium efektywności (ang. speed ) związaną z kosztem obliczeniowym wynikającym z wygenerowania i zastosowania klasyfikatora. W analizowanych danych pojawiają się czasem „luki” czyli brakujące wartości danych, lub też dane przypadkowe, zaciemniające obraz (tzw. dane zaszumione). Zdolność modelu do poprawnej predykcji klas w przypadku pojawienia się wcześniej wspomnianych rodzajów danych niepożądanych ocenia się w kategorii kryterium odporności modelu (ang. robustness).

Przy analizie danych pochodzących z dużej bazy danych, istotnym czynnikiem oceny metody jest skalowalność czyli zdolność metody do konstrukcji klasyfikatora dla dowolnie dużych wolumenów danych. Otrzymany wynik metody klasyfikacji powinien być łatwo interpretowalny, z czym wiąże się następne kryterium interpretowalności (ang. interpretability ). Kryterium to odnosi się do stopnia w jakim konstrukcja klasyfikatora pozwala na zrozumienie mechanizmu klasyfikacji danych. Istnieją metody klasyfikacji, które charakteryzują się dużą dokładnością, np. sieci neuronowe, które jednakże nie pozwalają na zrozumienie mechanizmu samej klasyfikacji danych. W praktyce metody te są w praktyce mało przydatne. Każda dziedzina ma swoje specyficzne potrzeby, w związku z tym przy wyborze metody klasyfikacji kieruje się własnymi kryteriami, które spełniają specjalistyczne oczekiwania. Kryterium to ogólnie przyjęło nazwę kryterium dziedzinowo-zależnego.

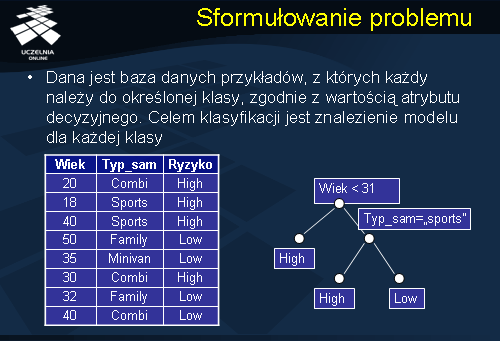
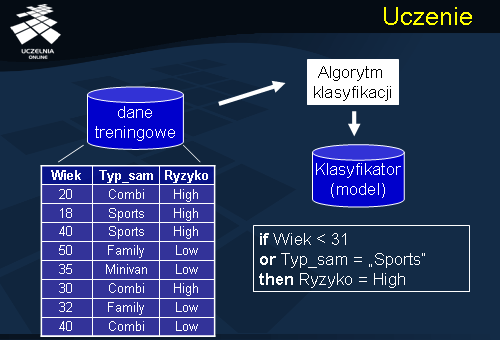
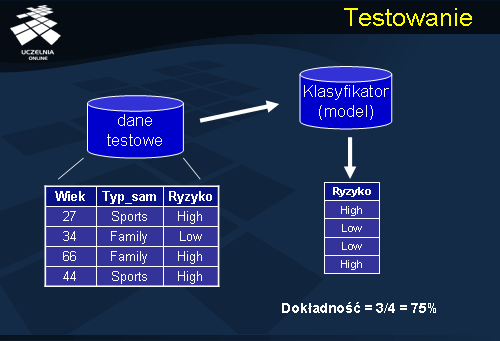
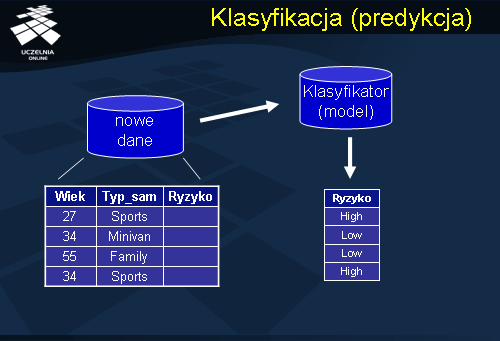
Przejdziemy teraz do sformułowania problemu klasyfikacji danych. Mamy daną bazę danych rekordów (przykładów), z których każdy posiada etykietę klasy, do której należy, zgodnie z wartością atrybutu decyzyjnego. Celem klasyfikacji będzie znalezienie modelu dla każdej klasy czyli opisu rekordów każdej z klas. Przykładowym problemem klasyfikacji może być automatyczny podział kierowców na powodujących i niepowodujących wypadki drogowe. Na powyższym slajdzie umieszczona została przykładowa baza danych, zawierającą informacje o wieku kierowcy, typie posiadanego samochodu oraz ryzyku związane z możliwością spowodowania wypadku. Dla powyższych danych, został zbudowany przykładowy model - klasyfikator w postaci drzewa decyzyjnego przedstawionego na slajdzie. Z podanego drzewa decyzyjnego, możemy odczytać następujące reguły decyzyjne: „Jeżeli kierowca ma poniżej 31 lat to ryzyko spowodowania wypadku jest duże”, inną reguła decyzyjną jest reguła: „Jeżeli kierowca ma powyżej 31 lat i dysponuje sportowym samochodem to ryzyko spowodowania wypadku jest duże”, wreszcie „Jeżeli kierowca ma powyżej 31 lat i typ samochodu jest różny od sportowego to ryzyko spowodowania wypadku jest niskie”.

W literaturze zaproponowano wiele metod klasyfikacji, jest to np: klasyfikacja poprzez indukcję drzew decyzyjnych, klasyfikatory Bayes’owskie, sieci neuronowe, analiza statystyczna, metaheurystyki (np. algorytmy genetyczne), zbiory przybliżone, metoda k-NN czyli k-najbliższych sąsiadów (ang. k-nearest neighbor ) i wiele innych statystycznych metod, które cały czas są rozwijane. Wśród wymienionych metod klasyfikacji najczęstszym jest metoda klasyfikacji poprzez indukcję drzew decyzyjnych, która jest szczególnie atrakcyjne dla eksploracji danych. Po pierwsze, dzięki intuicyjnej reprezentacji końcowy/otrzymany model klasyfikacji jest zrozumiały dla człowieka. Po drugie, drzewa decyzyjne mogą być konstruowane stosunkowo szybko w porównaniu z innymi metodami klasyfikacji. Kolejnym atutem drzew decyzyjnych jest, skalowalność dla dużych zbiorów danych i możliwość użycia wielowymiarowych danych. W dodatku dokładność drzew decyzyjnych jest porównywalna z innymi metodami klasyfikacji. Większość komercyjnych dostępnych narzędzi do eksploracji danych opiera się na modelu drzew decyzyjnych. Główną wadą drzew decyzyjnych jest niemożność wychwycenia korelacji pomiędzy atrybutami bez dodatkowych obliczeń. W następnej części wykładu przyjrzymy się bliżej wyżej wymienionej metodzie klasyfikacji.

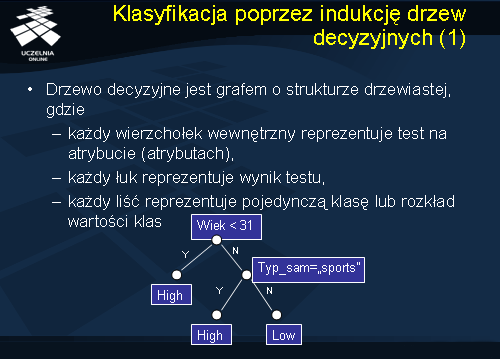
Wynikiem klasyfikacji w metodzie indukcji drzew decyzyjnych jest drzewo decyzyjne. Drzewo decyzyjne jest skierowanym acyklicznym grafem o strukturze drzewiastej, w którym każdy wierzchołek reprezentuje test na atrybucie (atrybutach), każdy łuk reprezentuje wynik testu, każdy liść reprezentuje pojedynczą klasę lub rozkład wartości klas. Najwyższy węzeł / wierzchołek drzewa nazywany rootem (korzeniem drzewa). Przyjrzyjmy się jeszcze raz przedstawionemu drzewu klasyfikacyjnemu z poprzedniego przykładu. W liściach mamy pojedynczą klasę lub rozkład wartości klas atrybuty decyzyjnego „Ryzyko”: (High,Low). Każdy wierzchołek wewnętrzny jest testem na atrybucie, natomiast łuk jest wynikiem testu (Y lub N).

Drzewo decyzyjne rekurencyjnie dzieli zbiór treningowy na partycje do momentu, w którym każda partycja zawiera dane należące do jednej klasy, lub, gdy w ramach partycji dominują dane należące do jednej klasy, natomiast rozmiar partycji jest ograniczony. Każdy wierzchołek wewnętrzny drzewa zawiera tzw. punkt podziału (ang . split point ), którym jest test na atrybucie (atrybutach), który dzieli zbiór danych na partycje.

Podstawowym algorytmem konstrukcji drzew decyzyjnych używanym w etapie konstrukcji jest algorytm zachłanny, który tworzy drzewo decyzyjne w rekurencyjny sposób techniką top-down w sposób „dziel i rządź” (ang. divide-and-conquer ). Istnieje wiele wariantów algorytmu podstawowego. Najczęściej stosowanymi algorytmami, pochodzącymi z uczenia maszynowego są algorytmy ID3 oraz C4.5 Inną techniką jest pochodzącą ze statystyki metoda CART, czy też metoda związana z rozpoznawaniem obrazów CHAID. Podstawową różnicą powyższych algorytmów jest przyjęte kryterium podziału, czyli sposobu w jaki tworzone są nowe węzły wewnętrzne w drzewie decyzyjnym, używanego podczas fazy budowania drzewa decyzyjnego. Metoda podziału powinna maksymalizować dokładność konstruowanego drzewa decyzyjnego, lub innymi słowy minimalizować błędną klasyfikację rekordów danych.

Drzewo decyzyjne jest zwykle konstruowane w dwóch fazach. W fazie pierwszej, zwanej fazą budowania, fazą wzrostu lub fazą indukcji drzew decyzyjnych, drzewo decyzyjne jest tworzone z treningowej bazy danych. W fazie drugiej, zwanej fazą obcinania lub redukcji drzewa (ang. pruning ), następuje obcinanie drzewa w celu poprawy dokładności, interpretowalności i uniezależnienia się od efektu przetrenowania. W fazie obcinania następuje identyfikacja i usunięcie gałęzi reprezentujące punkty osobliwe i szum.

Z przycinaniem drzewa wiążą się dwie główne strategie postpruning, w którym konstruujemy pełne drzewo decyzji i usuwamy z niego zawodne części. Strategia druga – prepruning - przestaje rozwijać gałąź, gdy informacje zaczynają być zawodne. W praktyce preferowany jest postpruning, gdyż prepruning często powoduje efekt „wczesnego stopu”.

Konstrukcja drzewa

---

Przyjrzymy się obecnie nieco dokładniej fazie konstrukcji drzewa decyzyjnego. W fazie konstrukcji drzewa, zbiór treningowy jest dzielony na partycje, rekurencyjnie, w punktach podziału do momentu, gdy każda z partycji jest „czysta” (zawiera dane należące wyłącznie do jednej klasy) lub liczba elementów partycji dostatecznie mała (spada poniżej pewnego zadanego progu). Postać testu stanowiącego punkt podziału zależy od kryterium podziału i typu danych atrybutu występującego w teście. Jak pamiętamy atrybuty mogą być typu ciągłego oraz typu kategorycznego. Dla atrybutu ciągłego A, test ma postać wartość(A) < x, gdzie x należy do dziedziny atrybutu A, x należy do dom(A), gdzie X zawiera się w dom(A). Dla atrybutu kategorycznego A, test ma postać wartość(A) należy do X, gdzie X jest podzbiorem dom(A).

Przejdźmy obecnie do przedstawienia algorytmu konstrukcji drzewa decyzyjnego. Prezentowany na slajdzie algorytm konstruuje binarne drzewo decyzyjne. Nie jest to algorytm ogólny, gdyż niektóre algorytmy klasyfikacji metodą indukcji drzew decyzyjnych konstruują drzewa decyzyjne, które nie są binarne, niemniej algorytm ten dobrze ilustruje mechanizm konstrukcji drzewa decyzyjnego. Podstawową procedurą prezentowanego algorytmu jest procedura Make Tree(Training Data D), której argumentem wejściowym jest cały zbiór danych treningowych D. Procedura Make Tree wywołuje procedurę Partition, której na początku parametrem wejściowym jest zbiór danych treningowych D. Budowa drzewa rozpoczyna się od pojedynczego węzła/wierzchołka zwanego korzeniem (root N node) reprezentującego treningową bazę danych D. Jeśli wszystkie krotki w D należą do tej samej klasy C, wówczas, węzeł N staje się liściem z etykietą C, i algorytm kończy swoje działanie. W przeciwnym razie, zbiór atrybutów A jest sprawdzany zgodnie z metodą selekcji podziału (split selection) SS i wybierany jest atrybut podziału zwany „best-split”. Atrybut podziału partycjonuje/dzieli zbiór treningowy D na zbiór oddzielnej klasy próbek S1, S2, ... Sv, gdzie Si=1,..,v zawiera wszystkie próbki ze zbioru D razem z punktem podziału. Gałąź, z etykietą Vi, jest tworzona dla każdej wartości ai atrybutu podziału, i dla każdej gałęzi Vi przydzielony jest zbiór próbek. Procedura partycjonowania jest powtarzana rekurencyjnie dla każdego węzła/wierzchołka potomka, przez co jest formowane drzewo decyzyjne dla każdej partycji przykładów. Procedura się kończy gdy każda z partycji jest „czysta” (zawiera dane należące wyłącznie do jednej klasy) lub liczba elementów partycji dostatecznie mała (spada poniżej pewnego zadanego progu).

W trakcie budowy drzewa decyzyjnego, musimy zwrócić szczególną uwagę na wybór takiego atrybutu i takiego punkt podziału, który określi wierzchołek wewnętrzny drzewa decyzyjnego, innymi słowy „najlepiej” podzieli zbiór danych treningowych należących do tego wierzchołka. Najczęstszą metodą wybieraną w systemach komercyjnych jest metoda, która polega na wyborze takiego atrybutu i takiego punktu podziału, który będzie minimalizował przyjęta miarę „zanieczyszczenia” zbioru danych. Metoda ta znajduje atrybut podziału wierzchołków drzewa decyzyjnego poprzez minimalizację miary „zanieczyszczenia”. Do oceny jakości punktu podziału zaproponowano szereg wskaźników (kryteriów), które przedstawimy na kolejnym slajdzie.

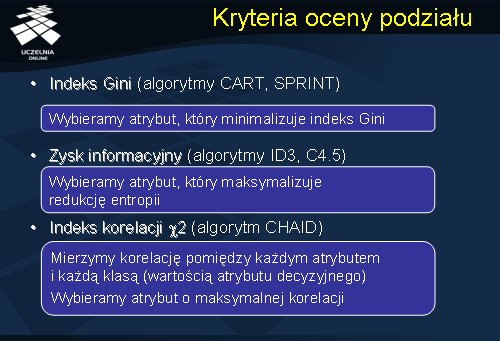
W literaturze zaproponowano szereg kryteriów oceny jakości punktu podziału, w praktyce w systemach komercyjnych wykorzystuje się trzy podstawowe kryteria. Mianowicie indeks gini, zysk informacyjny oraz indeks korelacji x2. W pierwszym przypadku wybieramy atrybut, który minimalizuje wartość indeksu gini, stosowany w algorytmach CART i SPRINT. W przypadku zysku informacyjnego stosowanego w algorytmach ID3 oraz C4.5 wybieramy atrybut, który maksymalizuje redukcję entropii. W przypadku indeksu korelacji x2 stosowanego w algorytmie CHAID mierzymy korelację pomiędzy każdym atrybutem i każdą klasą (wartością atrybutu decyzyjnego), ostatecznie wybieramy atrybut o maksymalnej korelacji.