Klasyfikacja II
Kontynuujemy prezentacje metod klasyfikacji. Na wykładzie zostaną przedstawione dwa podstawowe algorytmy klasyfikacji oparte o indukcję drzew decyzyjnych. Pierwszy z algorytmów wykorzystuje indeks Gini jako podstawowe kryterium oceny jakości podziału węzła w drzewie decyzyjnym, natomiast drugi z algorytmów wykorzystuje miarę Zysku Informacyjnego.
Indeks Gini

Jak zostało omówione wcześniej, jednym z newralgicznych punktów budowy drzewa decyzyjnego, jest wybór punktu podziału, który najlepiej wyznacza wierzchołek wewnętrzny drzewa decyzyjnego, innymi słowy „najlepiej” dzieli zbiór danych treningowych należących do tego wierzchołka. Popularnym kryterium oceny punktu podziału, stosowanym w wielu produktach komercyjnych, jest indeks Gini. Wykorzystuje się go między innymi w komercyjnym systemie IBM Inteligent Miner, w którym został zaimplementowany algorytm SPRINT. Rozważmy przykładowy zbiór treningowy, w którym każdy rekord opisuje ocenę ryzyka, że osoba, która ubezpieczyła samochód, spowoduje wypadek. Ocena została dokonana przez firmę ubezpieczeniową w oparciu o dotychczasową historię ubezpieczonego.
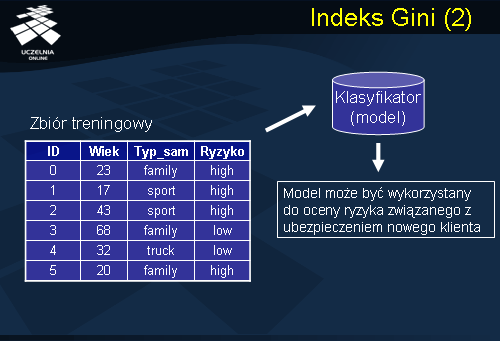
Dany jest zbiór treningowy przedstawiony na slajdzie. Zbiór treningowy zawiera dane opisujące ubezpieczonych, są to: identyfikator klienta, wiek ubezpieczonego, Typ_samochodu oznaczający typ posiadanego przez ubezpieczonego samochodu, oraz atrybut decyzyjny Ryzyko, określający czy ubezpieczony jest potencjalnym zagrożeniem na drodze, czy też poprawnym kierowcą bezwypadkowym. W oparciu o zbiór treningowy algorytm klasyfikacyjny konstruuje model (klasyfikator), który może być wykorzystany do oceny ryzyka związanego z ubezpieczeniem nowego klienta.

Przykładem algorytmu klasyfikacyjnego, który wykorzystuje mechanizm indukcji drzew decyzyjnych, który konstruuje binarne drzewo decyzyjne, który do oceny punktów podziału wykorzystuje indeks gini jest algorytm SPRINT. Algorytm SPRINT, jak już wspominaliśmy jest wykorzystywany w znanym i popularnym produkcie komercyjnym IBM Intelligent Miner. Konstrukcja drzewa decyzyjnego zgodnie z algorytmem SPRINT przebiega w następujący sposób: Podstawową procedurą tego algorytmu jest procedura Partition, której argumentem jest zbiór danych S. Jeżeli wszystkie próbki ze zbioru treningowego S należą do tej samej klasy, wówczas algorytm kończy działanie. Tworzy wierzchołek liścia i jego etykietą jest klasa, do której należą wszystkie obiekty należące do zbioru S. W przeciwnym wypadku algorytm, dla każdego atrybutu A analizuje wszystkie możliwe punkty podziału dla tego atrybutu. Następnie wybiera najlepszy punkt podziału spośród wszystkich możliwych punktów podziału dla wszystkich atrybutów. Wybieramy najlepszy punkt podziału i punkt ten dzieli nam zbiór S na partycje S1 i S2. Następnie wywoływana jest procedura Partition dla zbioru S1 i dla zbioru S2. Procedura jest wykonywana tak długo, aż każda z partycji zawiera dane należące wyłącznie do jednej klasy lub gdy liczba elementów partycji dostatecznie mała (spada poniżej pewnego zadanego progu).

Zanim przedstawimy szczegółowo mechanizm konstrukcji binarnego drzewa decyzyjnego zgodnie z algorytmem SPRINT, wprowadzimy dodatkowo dwie niezbędne definicje. Definicja 1 wartości indeksu gini dla zbioru S. Niech S oznacza zbiór przykładów należących do n klas. W danym węźle pj określa względną częstość występowania klasy j w zbiorze S. Wówczas wartość indeksu gini dla zbioru S jest równa różnicy przedstawionej na slajdzie. Przykładowo, jeżeli założymy, że zbiór S zawiera tylko i wyłącznie dwie klasy oznaczone Pos (pozytywne) i Neg (negatywne). Zakładamy, że mamy p elementów należących do klasy Pos i n elementów należących do klasy Neg, wówczas względna częstość występowania klasy Pos w zbiorze S wynosi p/(p+n). Natomiast względna częstość występowania klasy Neg w zbiorze S wynosi n/(n+p). Wartość indeksu gini dla zbioru S jest równa 1 - Ppos^2 - Pneg^2.

Wprowadzimy obecnie definicje indeksu podziału Gini. Punkt podziału dzieli zbiór S na dwie partycje S1 i S2. Indeks podziału Gini zbioru S na partycje S1 i S2 jest definiowany następująco: giniSPLIT(S) = (p1+ n1)/(p+n)*gini(S1) + (p2+ n2)/(p+n)* gini(S2), gdzie p1, n1 (p2, n2) oznaczają, odpowiednio:
-
p1 - elementów w S1 należących do klasy Pos,
-
n1 - liczba elementów w S1 należących do klasy Neg,
-
p2 - elementów w S2 należących do klasy Pos,
-
n2 - liczba elementów w S2 należących do klasy Neg

„Najlepszym” punktem podziału zbioru S, jak wspomnieliśmy wcześniej jest punkt podziału, który charakteryzuje się najmniejszą wartością indeksu podziału Gini. Wracając do prezentowanego wcześniej algorytmu SPRINT i procedury Partition, zauważmy, że kluczowym punktem tej procedury jest analiza dla każdego atrybutu wszystkich możliwych punktów podziału. Oznacza to, że dla każdego atrybutu, dla wszystkich możliwych punktów podziału, obliczamy wartość indeksu podziału Gini i wybieramy punkt podziału o najmniejszej wartości giniSPLIT . Wybrany punkt podziału włączamy do drzewa decyzyjnego jako wierzchołek wewnętrzny. Punkt podziału dzieli zbiór S na dwie partycje S1 i S2. Następnie powtarzamy procedurę obliczania indeksu podziału dla partycji S1 i S2, ponownie dla każdego atrybutu i wszystkich punktów podziału poszukujemy wartości indeksu podziału poszukujemy wartości indeksu podziału Gini. Wybieramy punkty podziału o najmniejszej wartości indeksu podziału Gini. Znalezione punkty podziału włączamy do drzewa decyzyjnego. Powtarzamy tę procedurę dla kolejnych partycji aż do osiągnięcia warunku stopu.
Przykład
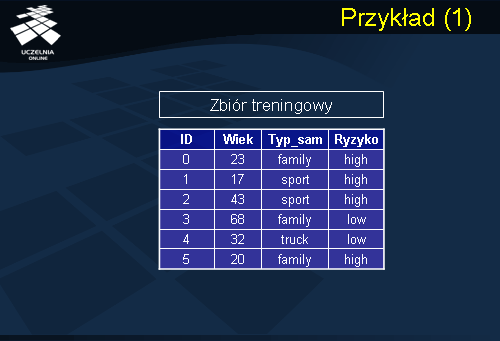
Aby zilustrować algorytm klasyfikacji wykorzystujący indukcję binarnego drzewa decyzyjnego i wykorzystujący do oceny punktów podziału indeks Gini, przeanalizujmy przykład przedstawiony na slajdzie. Dany jest zbiór treningowy, składający się z atrybutów opisujących klienta towarzystwa ubezpieczeniowego. Wiek ubezpieczonego, Typ_samochodu oznaczający typ posiadanego przez ubezpieczonego samochodu, oraz atrybut decyzyjny Ryzyko, oznaczający czy ubezpieczony jest potencjalnym zagrożeniem na drodze, czy też nie.
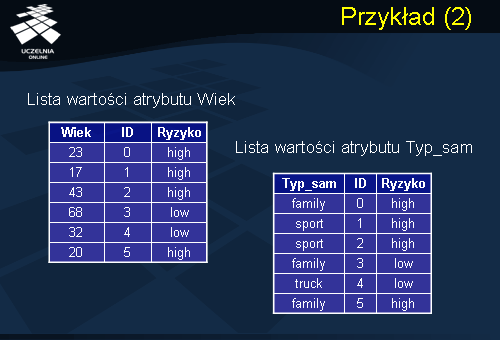
Zauważmy, że przedstawiony zbiór treningowy zawiera dwa atrybuty deskryptory oraz jeden atrybut decyzyjny Ryzyko. Deskryptory to atrybut numeryczny Wiek oraz atrybut kategoryczny Typ_samochodu. Lista wartości dla numerycznego atrybutu wiek została umieszczona w tabeli pierwszej przedstawiona po lewej stronie slajdu. Natomiast lista wartości atrybutu kategorycznego Typ_sam w tabeli drugiej.
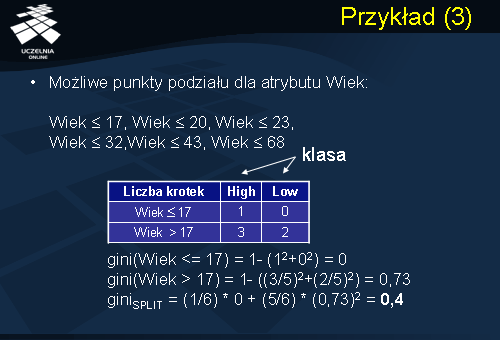
Zgodnie z procedurą Partition sprawdzamy, czy wszystkie rekordy zbioru treningowego należą do jednej klasy. Odpowiedź brzmi „nie”, ponieważ 4 rekordy zbioru treningowego należą do klasy Ryzyko = High i 2 rekordy należą do klasy Ryzyko = Low. Stąd przechodzimy do analizy atrybutów deskryptorów i wszystkich możliwych punktów podziału tych atrybutów. Rozpocznijmy od analizy atrybutu Wiek. Atrybut Wiek jest atrybutem numerycznym, stąd punkt podziału dla atrybutu numerycznego ma postać ‘wartość atrybutu numerycznego’ < lub <=. Przeanalizujmy wszystkie możliwe punkty podziału dla atrybutu Wiek:
Wiek <= 17, Wiek <= 20, Wiek <= 23, Wiek <= 32,Wiek <= 43, Wiek <= 68.
Ostatni punkt podziału Wiek <= 68 de facto tworzy nam podział na dwie partycje, z których jedna jest partycją pustą.
Rozpoczniemy od analizy pierwszego możliwego punktu podziału, Wiek <= 17. Zauważmy, że ten punkt podziału dzieli nam zbiór treningowy S na dwie partycje. Warunek Wiek <= 17 spełnia tylko jedna krotka, która należy do klasy Ryzyko = High. Pozostałe krotki należą do partycji S2 czyli spełniają warunek Wiek > 17. Takich krotek w zbiorze treningowym jest 5, z których trzy należą do klasy Ryzyko = High oraz dwie należą do klasy Ryzyko = Low. Obliczamy wartość indeksu Gini dla partycji pierwszej, czyli takiej, która spełnia predykat Wiek <= 17. Wartość ta wynosi 0. Następnie obliczamy wartość indeksu Gini dla drugiej partycji (Wiek>17). Wartość indeksu Gini wynosi 0.73. W oparciu o te wartości możemy następnie obliczyć wartość indeksu podziału Gini Split, który dla tego punktu podziału wynosi 0.4.
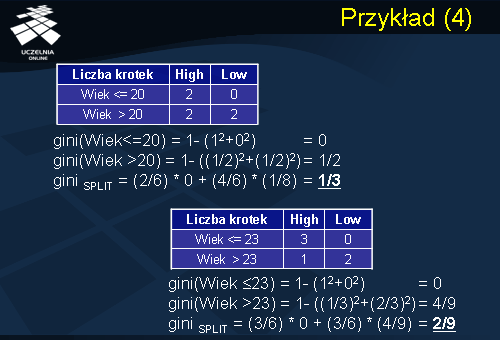
Rozważmy kolejny punkt podziału dla atrybutu Wiek. Jest nim punkt podziału Wiek<=20. Punkt podziału dzieli zbiór treningowy na partycje składająca się z dwóch rekordów. Oba rekordy należą do klasy Ryzyko = High. Partycja druga (Wiek>20), składa się z 4 rekordów, z których 2 rekordy należą do klasy Ryzyko = High i 2 rekordy należą do klasy Ryzyko = Low. Wartość indeksu Gini dla partycji pierwszej wynosi 0 – partycja czysta. Wartość indeksu Gini dla drugiej partycji, która jest równomiernie rozłożona pomiędzy klasy High i Low wynosi 1. Wartość indeksu podziału GiniSplit wynosi 1/3. Kolejny punkt podziału dla atrybutu Wiek to punkt podziału Wiek <= 23. Ten punkt podziału dzieli zbiór danych treningowych na partycje S1 składającą się z trzech rekordów. Wszystkie trzy rekordy należą do klasy Ryzyko = High. Natomiast partycja druga składa się również z trzech rekordów, jeden rekord należy do klasy Ryzyko = High oraz dwa rekordy Ryzyko = Low. Wartość indeksu Gini dla klasy pierwszej wynosi 0, czyli mamy klasę czystą (wszystkie rekordy należą do tej samej klasy). Wartość indeksu Gini dla drugiej partycji wynosi 4/9. Indeks podziału Gini wynosi 2/9.
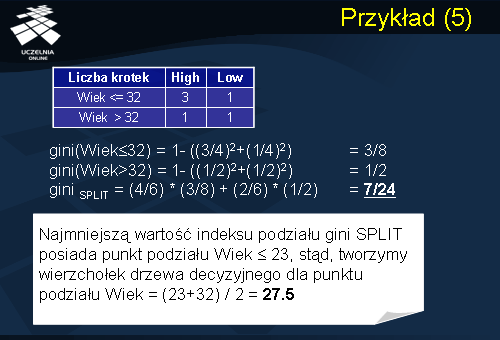
Rozważmy kolejny punkt podziału dla atrybutu Wiek, Wiek<=32. Ten punkt podziału dzieli zbiór treningowy na dwie partycje. Pierwsza partycja składa się z czterech rekordów, trzy z nich należą do klasy Ryzyko = High, oraz jeden do klasy Ryzyko = Low. Druga partycja zawiera dwa rekordy, po jednym z każdej klasy. Wartość indeksu Gini dla pierwszej partycji wynosi 3/8. Wartość indeksu Gini dla drugiej partycji wynosi 1. Wartość indeksu podziału GiniSplit wynosi 7/24. Pomińmy w naszych rozważaniach pozostałe punkty podziału. Z dotychczas rozważanych punktów podziału najmniejszą wartość indeksu podziału GiniSplit posiada punkt podziału Wiek<=23. Załóżmy również, że wartości indeksu podziału dla wszystkich punktów podziału dla deskryptora Typ_samochodu są większe aniżeli wartości indeksu dla punktów podziału dla atrybutu Wiek. Ponieważ najmniejszą wartość indeksu podziału GiniSplit posiada punkt podziału Wiek<=23 stąd tworzymy wierzchołek drzewa decyzyjnego. Jak ma wyglądać test dla takiego wierzchołka?. Atrybut Wiek jest atrybutem numerycznym, zatem test będzie wyglądał w następujący sposób: ‘Wiek <= ?’. Pojawia się pytanie czy ? Ma przyjąć wartość punktu podziału czyli wartość 23 czy też inną. Zastanówmy się nad następującym przypadkiem: Mamy nowego kierowcę w wieku 24 lat. Czy kierowca będzie się zachowywał jak kierowca 23 letni, dla którego ryzyko wypadku jest wysokie, czy też będzie się zachowywał jak kierowca 32 letni, dla którego ryzyko wypadku jest niskie. Odwróćmy sytuacje, mamy nowy przypadek: kierowca mający lat 31, czy kierowca będzie się zachowywał jak kierowca 32 letni, czy też jak kierowca 23 letni. Zauważmy, że pomiędzy wartościami 23 i 32 następuje punkt przecięcia. Stąd też tworzymy wierzchołek drzewa decyzyjnego dla punktu podziału, w którym wartość testu jest równa wartości (23 (przechowywana w bazie)+32(gdzie następuje zmiana przynależności do klasy))/2. Zatem punktem podziału, który będzie związany z nowym wierzchołkiem drzewa decyzyjnego będzie 27.5.

Po pierwszym podziale zbioru treningowego drzewo decyzyjne ma następującą postać przedstawioną na slajdzie. Korzeniem drzewa jest wierzchołek związany z punktem podziału Wiek<=27.5, z którego wychodzą dwie gałęzie. Pierwsza gałąź reprezentuje podział wiekowy <=27.5, druga gałąź reprezentuje rekordy dla których wartość atrybutu Wiek>27.5. Gałęzie te łączą wierzchołek korzenia z dwoma wierzchołkami, z którymi związane są dwie partycje. Do pierwszej partycji S1 należą wszystkie rekordy, dla których atrybut Wiek spełnia warunek Wiek<=27.5. Zauważmy, że pierwsza partycja S1 jest partycją „czystą”, w tym sensie, że wszystkie rekordy należące do tej partycji należą do jednej klasy. Wywołanie procedury Partition dla partycji S1, spowoduje zatrzymanie podziału i utworzenie wierzchołka liścia oraz związanie z tym wierzchołkiem etykiety Ryzyko = High. Natomiast druga partycja jest partycją, która nie jest czysta. Zawiera dwa rekordy, które należą do klasy Ryzyko = Low oraz jeden rekord należący do klasy Ryzyko = High. Jeżeli warunek stopu jest zdefiniowany w ten sposób, że liczba rekordów, które muszą należeć do danej partycji > 3, wówczas następuje zatrzymanie działania procedury Partition, utworzenie wierzchołka liścia i przydzielenie temu wierzchołkowi etykiety klasy, która dominuje w danym zbiorze partycji. Wówczas utworzony zostałby wierzchołek, który byłby wierzchołkiem liściem, którego wartość etykiety (klasy) byłaby równa Low.
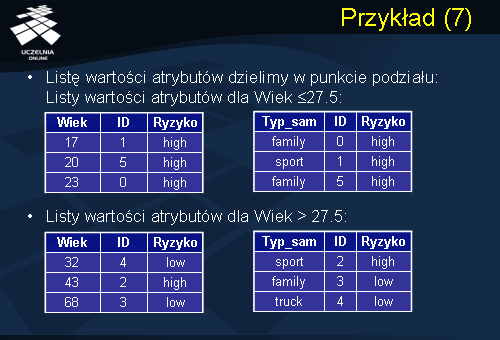
Jeżeli założymy, że minimalna liczba elementów partycji, która powoduje kontynuację wykonywania procedury Partition wynosi 5, wówczas po utworzeniu wierzchołka korzenia drzewa decyzyjnego procedura Partition zostaje zatrzymana i ostateczne drzewo decyzyjne skonstruowane przez algorytm Sprint będzie miało postać taką jak przedstawiona na poprzednim slajdzie. Jeżeli jednakże założymy, że minimalna liczba elementów partycji, która powoduje kontynuację wykonywania procedury Partition wynosi 3, wówczas konstrukcja drzewa decyzyjnego w rozważanym przez nas przykładzie będzie kontynuowana. W takim wypadku lista rekordów zbioru treningowego jest dzielona w punkcie podziału i uzyskujemy dwa zbiory rekordów, partycję pierwszą, która spełnia predykat Wiek <= 27.5, oraz partycję drugą, która spełnia warunek Wiek > 27.5. Przypomnijmy, że pierwsza partycja jest partycją czystą, w związku z tym tworzymy wierzchołek liścia, któremu przypisujemy etykietę klasy Ryzyko = High. Natomiast dla partycji drugiej uruchamiana jest procedura Partition, która ponownie dla każdego atrybutu deskryptora ocenia jakość wszystkich możliwych punktów podziału. Ponieważ lista atrybutów deskryptorów składa się w naszym przypadku tylko z dwóch atrybutów (Wiek oraz Typ_samochodu). Dodatkowo atrybut Wiek został wykorzystany do konstrukcji pierwszego wierzchołka drzewa decyzyjnego, to pozostaje nam do analizy tylko i wyłącznie atrybut Typ_samochodu, dla którego musimy dokonać oszacowania jakości wszystkich możliwych punktów podziału.

Musimy zatem dokonać oceny wszystkich możliwych punktów podziału dla atrybutu Typ_samochodu. Przypomnijmy, że atrybut Typ_samochodu jest atrybutem kategorycznym. Postać testu stanowiącego punkt podziału, dla atrybutu kategorycznego A ma następująca postać wartość A należy do X, gdzie X jest podzbiorem dom(A). Dziedzina wartości naszego atrybutu kategorycznego Typ_samochodu składa się z trzech elementów, samochód sport, samochód family oraz samochód truck. Liczba wszystkich możliwych punktów podziału atrybutu kategorycznego wynosi 2^N kombinacji, gdzie N oznacza liczbę wartości atrybutu kategorycznego. W naszym przypadku N wynosi 3, stąd liczba wszystkich możliwych punktów podziału wynosi 8. Zauważmy, że z punktu widzenia operacji zawierania się punkty podziału tworzą kratę, z której powinniśmy usunąć element minimalny i maksymalny ponieważ nie wnoszą one żadnego punktu podziału. Stąd też ostatecznie liczba punktów podziału, dla których należy dokonać oceny jakości punktu podziału wynosi 2^N-2.
Zatem możliwe punkty podziału to:
Typ_samochodu należy do zbioru {sport}, Typ_samochodu należy do zbioru {family}, Typ_samochodu należy do zbioru {truck},
Typ_samochodu należy do zbioru {family, sport}, Typ_samochodu należy do zbioru {truck, sport}, Typ_samochodu należy do zbioru {family, truck}.

Rozważmy pierwszy punkt podziału związany z testem, Typ_samochodu należy do kategorii samochód sportowy. Punkt podziału dzieli zbiór rekordów związanych z tworzonym wierzchołkiem na dwie partycje. Pierwsza partycja składa się z jednego rekordu, który spełnia predykat Typ_samochodu należy do kategorii samochód sportowy. Klasa związana z tym rekordem Ryzyko = High. Pozostała partycja składa się z dwóch rekordów, które należą do klasy Ryzyko = Low. Indeks Gini dla pierwszej partycji wynosi 0. Gini indeks dla drugiej partycji wynosi 0. Również indeks podziału Gini dla tego podziału wynosi 0. Rozważmy drugi punkt podziału związany z testem Typ samochodu należy do kategorii samochodów rodzinnych. Ten punkt podziały dzieli zbiór rekordów na dwie partycje. Pierwsza partycja składa się z jednego rekordu, który spełnia predykat Typ_samochodu należy do kategorii {family}, natomiast druga partycja składa się z dwóch rekordów. Pierwszy rekord należy do klasy Ryzyko = Low, natomiast druga partycja zawiera rekord, który należy do klasy Ryzyko = High oraz drugi rekord należący do klasy Ryzyko = Low. Indeks Gini pierwszej partycji wynosi 0, indeks Gini drugiej partycji wynosi 1. Indeks podziału Gini dla tego punktu podziału wynosi 1/3. W podobny sposób oceniamy wszystkie punkty podziału. Łatwo zauważyć, że istnieją dwa podziały, które charakteryzują się najmniejszą wartością. Pierwszy podział związany z testem Typ_samochodu należy do kategorii sportowy dla którego indeks podziału Gini wynosi 0. Drugi podział związany jest z testem Typ_samochodu należy do kategorii (family,truck} i indeks podziału dla tego podziału również wynosi 0.
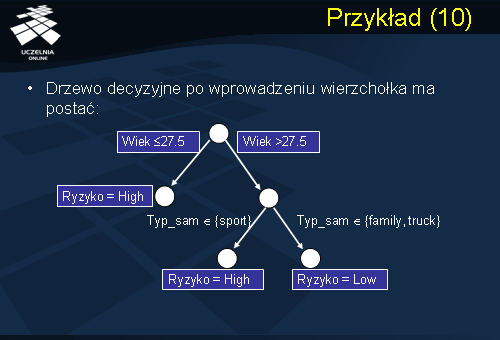
Jak już powiedzieliśmy najmniejszą wartość indeksu podziału Gini posiada punkt podziału Typ_sam należy do kategorii {sport}. Tworzymy wierzchołek wewnętrzny w drzewie decyzyjnym dla tego punktu podziału. Punkt podziału Typ_sam należy do kategorii {sport} dzieli zbiór krotek związanych z tym wierzchołkiem na dwie partycje. Pierwsza partycja składa się z jednego rekordu, która spełnia ten predykat i który należy do klasy Ryzyko = High. Druga partycja składa się z dwóch rekordów należących do klasy Ryzyko = Low. Ponieważ obie partycje są „czyste” kończy to konstrukcję drzewa decyzyjnego. Drzewo decyzyjne po wprowadzeniu wierzchołka wewnętrznego będzie miało postać przedstawioną na slajdzie.
Zysk informacyjny

Inną popularną grupą algorytmów indukcji drzew decyzyjnych są algorytmy, które do oceny punktu podziału wykorzystują kryterium zysku informacyjnego. Do tej grupy algorytmów należą takie popularne algorytmy jak algorytm ID3 oraz algorytm C 4.5. W algorytmach tych punktem podziału jest cały atrybut. Problem konstrukcji drzewa decyzyjnego przy użyciu miary zysku informacyjnego może być przedstawiony następująco. Najpierw zostaje wybrany atrybut, który jest korzeniem drzewa decyzyjnego. Dla każdej wartości wybranego atrybutu tworzona jest gałąź w tym drzewie decyzyjnym, z którą będzie związany zbiór rekordów posiadający tą samą wartość wybranego atrybutu. Następnie proces partycjonowania jest powtarzany dla każdej partycji związanej z każdą gałęzią. Jeżeli wszystkie rekordy podanego węzła należą do tej samej klasy, proces partycjonowania jest zakończony, dalszy podział węzłów jest niepotrzebny. Jeżeli nie, wówczas proces partycjonowania zbioru rekordów związany z daną gałęzią jest kontynuowany. W jaki sposób wybieramy atrybut związany z punktem podziału. Taki atrybut będziemy nazywać atrybutem testowym. Jako atrybut testowy (aktualny wierzchołek drzewa decyzyjnego) wybieramy atrybut o największym zysku informacyjnym (lub największej redukcji entropii). Z teorii informacji okazuje się, że atrybut który gwarantuje największy zysk informacyjny jest to atrybut, który który minimalizuje ilość informacji niezbędnej do klasyfikacji przykładów w partycjach uzyskanych w wyniku podziału.

Przejdziemy obecnie do formalnego zdefiniowania kryterium zysku informacyjnego oraz przedstawienia metody podziału w oparciu o to kryterium zysku informacyjnego. Niech S oznacza zbiór s przykładów. Załóżmy, że atrybut decyzyjny posiada m różnych wartości definiujących m klas, Ci (dla i=1, ..., m). Niech si oznacza liczbę przykładów zbioru S należących do klasy Ci. Zgodnie z teorią informacji oczekiwana ilość informacji niezbędna do zaklasyfikowania danego przykładu, możemy przedstawić wzorem podanym na slajdzie. Oczekiwana ilość informacji niezbędna do zaklasyfikowania danego przykładu jest wartością stałą dla danego zbioru S.

Niech pi oznacza prawdopodobieństwo, że dowolny przykład należy do klasy Ci (oszacowanie - si/s).
Zakładamy, że atrybut A posiada v różnych wartości: {a1, a2, ..., av}.
Atrybut A dzieli zbiór S na partycje {S1, S2, ..., Sv}, gdzie Sj zawiera przykłady ze zbioru S, których wartość atrybutu A wynosi aj. Wybierając atrybut A jako atrybut testowy tworzymy wierzchołek wewnętrzny drzewa, którego łuki wychodzące posiadają etykiety {a1, a2, ..., av} i łączą dany wierzchołek A z wierzchołkami zawierającymi partycje {S1, S2, ..., Sv}.

Niech sij oznacza liczbę przykładów z klasy Ci w partycji Sj. Entropię podziału zbioru S na partycje, według atrybutu A definiujemy wzorem przedstawionym na slajdzie. Można łatwo zauważyć, że entropia jest miarą nieuporządkowania zbioru S zgodnie z atrybutem A. Im mniejsza wartość entropii tym większa „czystość” podziału zbioru S na partycje, tzn. uzyskane w wyniku podziału partycje będą tym czystsze im mniejsza jest wartość entropii.

Współczynnik (s1j + s2j +...+smj)/s stanowi wagę j-tej partycji i zdefiniowany jest jako iloraz liczby przykładów w j-tej partycji (i.e. krotek posiadających wartość aj atrybutu A) do całkowitej liczby przykładów w zbiorze S. Zauważmy, że dla danej partycji Sj, wyrażenie I(s1j + s2j +...+ smj) podane wzorem przedstawionym na slajdzie, definiuje nam oczekiwaną ilość informacji niezbędną do zaklasyfikowania danego przykładu w partycji sj do określonej klasy. Jak łatwo zauważyć oczekiwana ilość informacji niezbędna do zaklasyfikowania danego przykładu jest równa 0 jeżeli cała partycja jest czysta, czyli należy do jednej klasy. W przeciwnym razie wartość tego wyrażenia określa nam nieuporządkowanie (nieczystość) partycji sj.

Zauważmy, że definicja entropii, przedstawiona na slajdzie 21 jest zagregowaną sumą wyrażeń I(s1j,s2j,…,smj) dla każdej partycji sj. Jeżeli podział zbioru S na partycje wg atrybutu A tworzy nam partycje czyste to dla każdej partycji sj wyrażenie I(s1j,s2j,…,smj) będzie równe 0 i zagregowana suma również będzie 0. Co oznacza, że wartość entropii podziału zbioru S na partycje czyste będzie wynosiła 0. Korzystając z tego faktu możemy obecnie zdefiniować miarę zysku informacyjnego wynikającego z podziału zbioru S na partycje wg atrybutu A. Zysk informacyjny definiujemy zgodnie ze wzorem przedstawionym na slajdzie. Zysk informacyjny wynikający z podziału zbioru S na partycje wg atrybutu A jest równy oczekiwanej ilości informacji niezbędnych do zaklasyfikowania danego przykładu należącego do zbioru S minus entropia atrybutu A. Zwróćmy uwagę, że zysk informacyjny oznacza oczekiwaną redukcję nieuporządkowania spowodowaną znajomością wartości atrybutu A.
Przykład 2
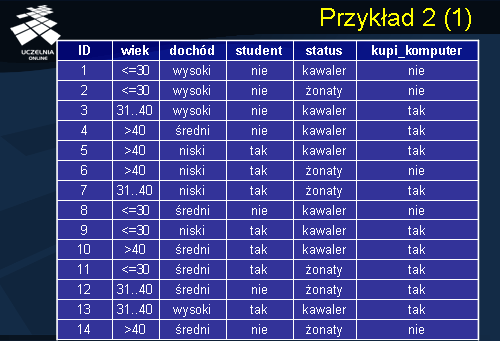
Dla ilustracji działania algorytmu indukcji drzewa decyzyjnego wykorzystującego miarę zysku informacyjnego rozważmy przykład przedstawiony na slajdzie. Dany jest zbiór treningowy zawierający informację o klientach sklepu komputerowego. Atrybuty opisujące klienta zawierają informacje na temat jego grupy wiekowej, dochodu, statusu, informacji o przynależności do grupy student. Atrybutem decyzyjnym jest atrybut Kupi_komputer zawierający informacje czy klient potencjalnie dokona zakupu sprzętu komputerowego czy też nie. Powyższy przykład zaczerpnięty został z podręcznika J.Han’a.

Rozważany przez nas zbiór treningowy S składa się z 14 przykładów. Atrybut decyzyjny, „kupi_komputer”, posiada dwie wartości (tak, nie), stąd, wyróżniamy dwie klasy. Klasa C1 odpowiada wartości „tak”, natomiast klasa C2 odpowiada wartości „nie”. S1 – liczba przykładów zbioru S należących do C1 i wynosi 9. S2 - liczba przykładów należących do klasy C2 wynosi 5. Podstawiając do wzoru na oczekiwanej ilości informacji niezbędnych do zaklasyfikowania danego przykładu należącego do zbioru S , wynosi 0.94.

Następnie, w kolejnym kroku przechodzimy do obliczenia entropii podziału zbioru S na partycje wg wszystkich atrybutów deskryptorów.
W rozważanym przez nas przykładzie mamy 4 atrybuty deskryptory. Są to atrybut Wiek, Dochód, Student oraz atrybut Status. Rozpocznijmy od analizy atrybutu Wiek. Załóżmy, że atrybut Wiek jest naszym atrybutem testowym. Atrybut Wiek dzieli zbiór S na 3 partycje:S1,S2 i S3. Pierwsza partycja S1 dla wartości Wiek<=30 składa się z pięciu przykładów. S11 – liczba przykładów z klasy C1 partycji S1 wynosi 2, natomiast liczba przykładów z klasy C2 partycji S1 wynosi 3. Podstawiając te wartości do wyrażenia I(S11,S21)=0.971. Zauważmy, że dla partycji S2 – partycja składa się z 4 rekordów. Wszystkie 4 rekordy należą do klasy C1. Partycja ta jest czysta, stąd też wartość wyrażenia I(S12.S22)=0. Dla partycji S3 związanej z wartością wyrażenia wiek=>40, partycja składa się z 5 rekordów, z czego 2 rekordy należą do klasy C1 i 3 rekordy należą do klasy C2. Stąd też wartość wyrażenia I(S13,S23)=0.971.

Entropia podziału zbioru S na partycje wg atrybutu A zgodnie ze wzorem ze slajdu 21 wynosi 0.694. Zauważmy, że wagi wyrażeń I we wzorze na entropię są równe: 5/14 ponieważ partycja S1 składa się z 5 rekordów natomiast cały zbiór treningowy zawiera 14 rekordów, 4/14 – partycja S2 składa się z 4 rekordów i partycja S3 składa się z 5 rekordów. Zysk informacyjny wynikający z podziału zbioru S wg atrybutu wiek wynosi 0.246 i jest równy różnicy wartości oczekiwanej ilości informacji niezbędnej do zaklasyfikowania dowolnego przykładu ze zbioru S minus entropia atrybutu Wiek.

W analogiczny sposób obliczamy zysk informacyjny dla pozostałych atrybutów dochód, student oraz status. Ponieważ Wiek daje największy zysk informacyjny spośród wszystkich deskryptorów, atrybut ten jest wybierany jako pierwszy atrybut testowy. Tworzymy wierzchołek drzewa o etykiecie Wiek, oraz etykietowane łuki wychodzące łączące wierzchołek Wiek z wierzchołkami odpowiadającymi partycjom S1,S2 oraz S3 utworzonymi zgodnie z podziałem zbioru S wg atrybutu Wiek.
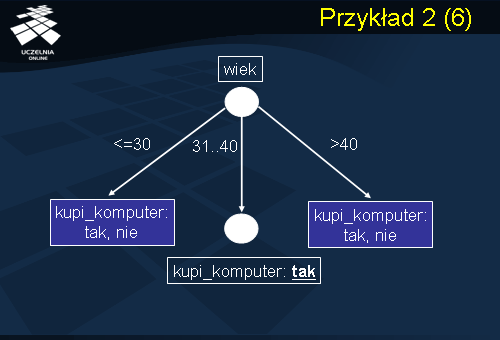
W ten sposób otrzymujemy drzewo decyzyjne przedstawione na slajdzie, które zawiera korzeń związany z atrybutem testowym wiek, charakteryzującym się największym zyskiem informacyjnym oraz trzy gałęzie wychodzące etykietowane wartościami atrybutu Wiek<=30 , 31..40 oraz >40. Gałęzie te łączą korzeń z wierzchołkami reprezentującymi partycje S1, S2 i S3. Zauważmy, że partycja S2 jest partycją czystą, czyli zawiera rekordy należące do tej samej klasy kupi_komputer = tak. Przekształcamy zatem ten wierzchołek liścia, który etykietujemy wartością klasy kupi_komputer = tak. Dla pozostałych partycji S1 i S3 kontynuujemy proces partycjonowania i tworzenia drzewa decyzyjnego.
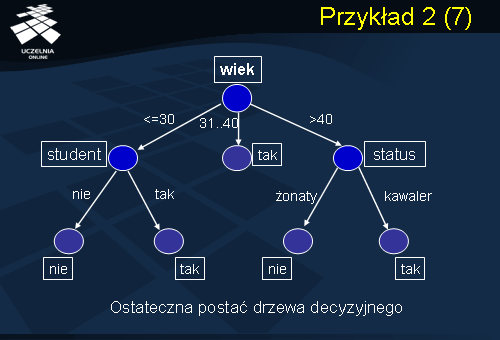
Okazuje się z dalszych obliczeń, że najlepszym atrybutem testowym dla partycji S1 jest atrybut Student, charakteryzujący się największym zyskiem informacyjnym, który dzieli partycję S1 na dwie partycje, które są partycjami czystymi. Dla wartości atrybutu Student = nie otrzymujemy partycję, której wszystkie rekordy należą do klasy C2. Natomiast dla wartości atrybutu Student = tak wszystkie rekordy należą do klasy kupi komputer = tak. W przypadku partycji S3 najlepszym atrybutem testowym jest atrybut Status, który dzieli rekordy partycji S3 na dwie partycje. Pierwsza partycja zawiera wszystkie rekordy, dla których Status = żonaty. Druga partycja zawiera rekordy, dla których Status = kawaler. Obie otrzymane partycje są czyste. Partycja związana z atrybutem Status z wartością żonaty tworzy wszystkie rekordy należą do C2. Natomiast w przypadku atrybutu Status = kawaler, wszystkie rekordy należą do klasy C1. Ostateczna postać drzewa decyzyjnego, uzyskanego metodą indukcji z wykorzystaniem jako kryterium miary zysku informacyjnego jest przedstawiona na slajdzie. Zauważmy, że pojawiły się dwa nowe wierzchołki (punkty podziału) związane z atrybutem Status oraz z atrybutem Student. To kończy konstrukcję drzewa decyzyjnego i rozważany przez nas przykład.




























