Kontynuujemy prezentację zagadnień związanych z klasyfikacją. Na początku przedstawimy technikę przycinania drzew decyzyjnych. W dalszej części omówimy dwie inne metody klasyfikacji, mianowicie Naiwny klasyfikatorowi Bayes’a, oraz metodę k-najbliższych sąsiadów. Na zakończenie wrócimy do zagadnienia związanego z dokładnością klasyfikacji oraz metodami weryfikacji dokładności klasyfikacji.


Obcinanie drzewa

---

Jak wspominaliśmy wcześniej na jednym z wykładów poświęconych klasyfikacji, faza konstrukcji drzewa decyzyjnego składa się de facto z dwóch etapów. Kroku konstrukcji drzewa oraz kroku przycinania drzewa decyzyjnego. Problem polega na tym, że po zakończeniu fazy konstrukcji drzewa decyzyjnego wiele gałęzi tego drzewa odzwierciedla anomalie w zbiorze danych treningowych w postaci danych zaszumionych oraz punktów osobliwych. Rozwiązaniem tego problemu jest przycięcie drzewa decyzyjnego. Przycięcie polega na usunięciu mało wiarygodnych gałęzi, co poprawia z jednej strony czytelność klasyfikatora, jego interpretowalność z drugiej strony poprawia zdolność klasyfikatora do klasyfikacji nowych przypadków. Istnieje wiele metod przycinania drzew decyzyjnych, większość z nich bazuje na pewnych miarach statystycznych np. miara MDL.

Jak już wspominaliśmy wcześniej na jednym z wykładów znane są dwa podejścia do problemu przycinania drzew decyzyjnych. Podejście pierwsze tzw. podejście polegające na wstępnym przycinaniu drzewa decyzyjnego, czasami używamy określenia prepruningu, oraz podejście drugie, które polega na przycinaniu drzewa po zakończeniu konstrukcji drzewa decyzyjnego nazwane czasami podejściem postpruningu. Podejście pierwsze tzn. wstępne przycinanie drzewa polega na przycięciu drzewa przez wcześniejsze zatrzymanie procedury konstrukcji drzewa. Wprowadzamy warunek stopu, który wstrzymuje dalsze dzielenie zbioru treningowego na partycje. Przykładowym warunkiem stopu, który można wykorzystać do wstrzymania dalszego dzielenia zbioru treningowego jest warunek stopu polegający na przyjęciu minimalnej liczby elementów należących do partycji, która podlega dzieleniu. Drugie podejście, czyli podejście polegające na przycinaniu drzewa decyzyjnego po zakończeniu konstrukcji drzewa, bazuje na miarach statystycznych jak wspomnieliśmy wcześniej np. miara MDL. Podstawowym celem przycinania, jak to zostało wcześniej powiedziane jest z jednej strony poprawa zdolności klasyfikatora do klasyfikacji nowych przypadków, z drugiej strony celem przycinania drzew jest poprawa interpretowalności i czytelności klasyfikatora.

Rozważmy drzewo decyzyjne, prezentowane w przykładzie nr 2 na poprzednim wykładzie. Drzewo decyzyjne z tego przykładu można przedstawić w postaci następującego zbioru reguł klasyfikacyjnych uzyskanych dla wszystkich ścieżek łączących korzeń drzewa decyzyjnego ze wszystkimi liśćmi. Otrzymujemy następujący zbiór reguł:

Jeżeli wiek ‘<= 30’ i student = ‘nie’ wówczas (THEN) kupi_komputer = ‘nie’.

Następne ścieżki:

Jeżeli wiek =‘<=30’AND student=‘tak’THEN kupi_komputer=‘tak’

Jeżeli wiek =’31..40’THEN kupi_komputer =‘tak’

Jeżeli wiek =‘>40’ AND status=‘żonaty’THEN kupi_komputer =‘nie’

Jeżeli wiek =‘>40’ AND status =‘kawaler’THEN kupi_komputer =‘tak’

Przejdziemy obecnie do przedstawienia innych metod klasyfikacji. Rozpoczniemy od krótkiego przedstawienia metody klasyfikacji asocjacyjnej. Zauważmy, że reguły klasyfikacyjne, które prezentowaliśmy uprzednio w swoim schemacie przypominają wielowymiarowe reguły asocjacyjne. Pojawia się pytanie ‘Czy możemy zastosować algorytmy odkrywania wielowymiarowych reguł asocjacyjnych do odkrywania reguł klasyfikacyjnych ze zbioru danych treningowych?’. Odpowiedź na postawione pytanie jest pozytywna, niemniej sam proces odkrywania reguł klasyfikacyjnych wymaga pewnej modyfikacji. Zauważmy jaka jest różnica pomiędzy wielowymiarową regułą asocjacyjną a regułą klasyfikacyjną.

Reguła klasyfikacyjna ma postać condset -> y, gdzie condset jest zbiorem par atrybut-wartość, natomiast y oznacza wartość atrybutu decyzyjnego. W przypadku wielowymiarowych reguł asocjacyjnych, następnikiem reguły może być wartość dowolnego atrybutu, niekoniecznie atrybutu decyzyjnego. Stąd zastosowanie algorytmów odkrywania wielowymiarowych reguł asocjacyjnych do odkrywania reguł klasyfikacyjnych jest procesem dwuetapowym. W pierwszym etapie, dla danego zbioru danych treningowych generujemy wszystkie możliwe wielowymiarowe reguły asocjacyjne, a następnie w kolejnym kroku eliminujemy te wielowymiarowe reguły asocjacyjne, dla których następnikiem reguły niejest wartość atrybutu decyzyjnego.

Przejdziemy obecnie do przedstawienia innej bardzo popularnej metody klasyfikacji, mianowicie Naiwnego klasyfikatora Bayes’a. Naiwny klasyfikator Bayes’a jest jedną z metod uczenia maszynowego, stosowaną do rozwiązywania problemu sortowania i klasyfikacji. Zadaniem klasyfikatora Bayes’a jest przyporządkowanie nowego przypadku do jednej z klas decyzyjnych, przy czym zbiór klas decyzyjnych musi być skończony i zdefiniowany apriori. Naiwny klasyfikator Bayes’a jest statystycznym klasyfikatorem, opartym na twierdzeniu Bayesa.

Pod względem wydajnościowym, Naiwny klasyfikator Bayes’a jest porównywalny do algorytmów klasyfikacji metodą indukcji drzew decyzyjnych oraz metod klasyfikacji opartej o sieci neuronowe. Charakteryzuje się dużą dokładnością i skalowalnością nawet dla bardzo dużych wolumenów danych. Naiwny klasyfikator Bayes’a zakłada, że wartości atrybutów w klasach są niezależne. Założenie to jest zwane założeniem o niezależności warunkowej klasy (ang. class conditional independence). Zanim przedstawimy szczegółowo Naiwny klasyfikator Bayes’a, wprowadzimy kilka pojęć oraz przypomnimy podstawowe twierdzenie Bayes’a. Niech X oznacza przykład, którego klasa nie jest znana. Załóżmy, że każdy przykład jest reprezentowany w postaci n-wymiarowego wektora, X=(x1, x2, …,xn). P(C|X) oznacza prawdopodobieństwo a-posteriori, że przykład X należy do klasy C.

Naiwny klasyfikator Bayes’a opiera się na regule Bayes’a, zgodnie z którą przykład X klasyfikujemy jako pochodzący z tej klasy Ci, dla której wartość P(Ci|X), i = 1, 2, ..., m, jest największa. Zwróćmy jeszcze uwagę, że Naiwny klasyfikator Bayes’a różni się od zwykłego klasyfikatora tym, że konstruując go zakładamy wzajemną niezależność atrybutów opisujących każdy przykład.

Przykładowo, niech dany będzie zbiór przykładów opisujących wnioski kredytowe klientów banku. P(Ryzyko=niskie | Wiek=38, Status=rozwodnik, Dochód=niski, Dzieci=2) oznacza, ze prawdopodobieństwo a-posteriori, że klient, X=(38, rozwodnik, niski, 2), składający wniosek kredytowy jest klientem o niskim ryzyku kredytowym (klient wiarygodny).

W jaki sposób szacujemy prawdopodobieństwo a-posteriori, że przykład X należy do klasy C?

Korzystamy z twierdzenia Bayesa, które brzmi następująco: P(C|X) = (P(X|C) * P(C))/P(X). Gdzie P(C) oznacza prawdopodobieństwo a priori wystąpienia klasy C, czyli prawdopodobieństwo, że dowolny przykład należy do klasy C). Prawdopodobieństwo P(X|C) oznacza prawdopodobieństwo a-posteriori, że X należy do klasy C, natomiast P(X) oznacza prawdopodobieństwo a priori wystąpienia przykładu X.

Załóżmy, że dany jest zbiór treningowy D składający się z n przykładów. Zakładamy, że atrybut decyzyjny przyjmuje m różnych wartości definiując m różnych klas Ci, i = 1, ..., m. Niech si oznacza liczbę przykładów ze zbioru treningowego D należących do klasy Ci. Naiwny klasyfikator Bayesa przypisuje nieznany przykład X do tej klasy Ci, dla której wartość P(C_i|X) jest największa.

Prawdopodobieństwo P(X) jest stałe dla wszystkich klas, zatem klasa Ci, dla której wartość P(Ci|X) jest największa, to klasa Ci, dla której wartość P(X| Ci) * P(Ci) jest największa. Jeżeli chodzi o prawdopodobieństwo apriori wystąpienia klasy Ci, mamy dwie możliwości. Możemy założyć, w bardzo dużym uproszczeniu, że wystąpienie każdej klasy posiada to samo prawdopodobieństwo. Innymi słowy, możemy przyjąć założenie, że prawdopodobieństwo P(C1) = P(C2) = ... = P(Cm). Możemy też zastąpić wartość wystąpienia apriori klasy Ci, estymatorem si/n, tzn. względną częstością występowania klasy Ci w zbiorze przykładów D.

W jaki sposób obliczyć P(X|Ci)? Dla dużych zbiorów danych, o dużej liczbie deskryptorów, obliczenie P(X|Ci) będzie operacją bardzo kosztowną. Wymaga ono bowiem oszacowania ogromnej liczby prawdopodobieństw i jest rzędu k^p, gdzie p oznacza zmienne, natomiast k oznacza liczbę wartości tych zmiennych, np. dla p=30 zmiennych binarnych (przyjmujących tylko dwie wartości) musielibyśmy oszacować liczbę prawdopodobieństw rzędu 2^30 czyli około 10^9. Rozwiązaniem tego problemu jest przyjęcie założenie o niezależności atrybutów. (ang. class conditional independance). Przypomnijmy, że mówiliśmy wcześniej, że możemy przyjąć, że wszystkie zmienne są warunkowo niezależne przy danych klasach. Wówczas możemy zastąpić prawdopodobieństwo warunkowe P(X|Ci) iloczynem prawdopodobieństw zgodnie z formułą przedstawioną na slajdzie.

Założenie o warunkowej niezależności zmiennych przy danych klasach nazywamy czasami naiwnym założeniem Bayes’a. Przedstawiona na poprzednim slajdzie aproksymacja pozwala przybliżyć pełny rozkład warunkowy wymagający oszacowania kp liczby prawdopodobieństw iloczynem rozkładów jednowymiarowych wymagających w sumie oszacowania kp prawdopodobieństw na klasę. Model warunkowej zależności jest zatem liniowo a nie wykładniczo zależny od liczby zmiennych p. W jaki sposób szacujemy, że prawdopodobieństwa warunkowe P(x1|Ci), P(x2|Ci), ..., P(xn|Ci). Prawdopodobieństwa te można estymować w oparciu o zbiór treningowy następująco:

- jeżeli j-ty atrybut jest atrybutem kategorycznym, to P(xj|Ci) estymujemy względną częstością występowania przykładów z klasy Ci posiadających wartość xj dla j-tego atrybutu, (sij/si).

- jeżeli j-ty atrybut jest atrybutem ciągłym, to P(xj|Ci) estymujemy funkcją gęstości Gaussa przedstawioną na slajdzie przy założeniu rozkładu normalnego wartości atrybutów.

Dla ilustracji działania naiwnego klasyfikatora Bayes’owskiego rozważmy przykład 2 z poprzedniego wykładu. Dany jest zbiór treningowy składający się z 14 przykładów, atrybutem decyzyjnym jest atrybut kupi_komputer, który przyjmuje dwie wartości ‘tak’ lub ‘nie’. Wartości te wyznaczają dwie klasy C1 i C2. Klasa C1 wyznaczona jest przez wartość atrybutu decyzyjnego kupi_komputer = ‘tak’, natomiast klasa C2 wyznaczona jest przez wartość atrybutu decyzyjnego kupi_komputer = ‘nie’. Rozważmy nowy przypadek X opisany następującymi wartościami deskryptorów, mianowicie atrybut wiek<=30, atrybut dochód = ‘średni’, atrybut student = ‘tak’ oraz atrybut status = ‘kawaler’. Do której klasy decyzyjnej zostanie zaklasyfikowany nowy przypadek X zgodnie z naiwnym klasyfikatorem Bayes’a? Przypomnijmy, że zgodnie z regułą Bayes’a nowy przypadek X zostanie zaklasyfikowany do tej klasy Ci, dla której prawdopodobieństwo P(X|Ci) jest największe.

Aby wyznaczyć klasę decyzyjną do której zostanie zaklasyfikowany nowy przypadek X rozpocznijmy od oszacowania prawdopodobieństw apriori wystąpienia poszczególnych klas tzn. klasy C1 oraz C2. Przypomnijmy, że oszacowania prawdopodobieństwa apriori wystąpienia klasy C1 i C2 zastępujemy estymatorami, (względną częstością występowania klasy Ci). W związku z tym oszacowanie prawdopodobieństwa wystąpienia klasy C1 tzn. atrybut decyzyjny kupi_komputer = ‘tak’ wynosi 9/14 czyli 0.643. Oszacowanie prawdopodobieństwa apriori wystąpienia klasy C2, podobnie jak poprzednio zastępujemy estymatorem S2n, i wynosi ono 5/14=0.357. Wynika to z faktu, że w pięciu przypadkach na 14 wartość atrybutu decyzyjnego kupi_komputer = ‘nie’. W kolejnym kroku, zgodnie z formułą przedstawioną na slajdzie nr 13, podajemy oszacowania prawdopodobieństw wartości x1 dla klasy C1, prawdopodobieństwa x1 dla klasy C2, wartości x2 dla klasy C1, wartości x2 dla klasy C2 itd. Przypomnijmy, że wartość x1 tj. wartość atrybutu wiek<=30. Klasa C1 kupi_komputer = ‘tak’. Zgodnie z estymatami podanymi na slajdzie 14 prawdopodobieństwo, że wartość x1 należy do klasy C1, w przypadku gdy atrybut jest atrybutem kategorycznym estymujemy względną częstością występowania przykładów z klasy C1 posiadających wartość xj dla j-tego atrybutu. W związku z tym prawdopodobieństwo wynosi 2/9 czyli 0.222, itd.

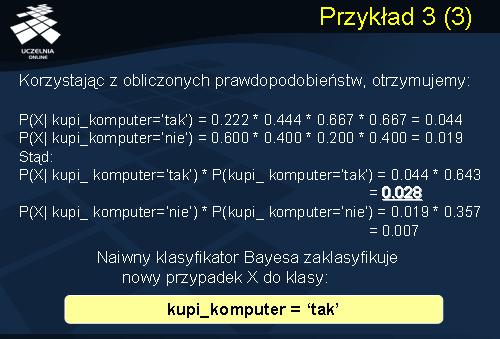
Korzystając z obliczonych oszacowań prawdopodobieństw warunkowych, że wartości x1, x2, x3 oraz x4 nowego przykładu X należą do klasy C1 i klasy C2, otrzymujemy następujące oszacowania prawdopodobieństw. Oszacowanie prawdopodobieństwa, że nowy przykład należy do klasy C1 jest iloczynem obliczonych prawdopodobieństw i wynosi 0.044. Prawdopodobieństwo, że nowy przykład należy do klasy C2 kupi_komputer = ‘nie’ wynosi 0.019. Podstawiając obliczone oszacowania prawdopodobieństw do wzoru przedstawionego na slajdzie nr 10, zakładając, że prawdopodobieństwo apriori wystąpienia dowolnego przykładu jest stałe, otrzymujemy następujące wartości prawdopodobieństw, że przykład X zostanie zaklasyfikowany do klasy C1 czyli klasy kupi_komputer = ‘tak’. Prawdopodobieństwo to wynosi 0.028. Prawdopodobieństwo, że nowy przykład zostanie zaklasyfikowany do klasy C2 wynosi 0.007. Stąd możemy wnioskować, że naiwny klasyfikator Bayes’a zaklasyfikuje nowy przypadek X do klasy decyzyjnej kupi_komputer = ‘tak’.

Na zakończenie omawiania naiwnego klasyfikatora Bayes’a, koniecznie musimy wspomnieć o problemie tzw. „częstości zero”. Zastanówmy się, co się stanie w przypadku gdy dana wartość atrybutu nie występuje dla wszystkich klas?

Przykładowo, w rozważanym przez nas przykładzie dla atrybutu wiek=’31..40’ nie występuje dla klasy decyzyjnej ‘nie’ czyli klasy C2. W konsekwencji prawdopodobieństwo, że nowy przykład dla którego wartość atrybutu wiek jest równa ’31..40’ należy do klasy C2 wynosi 0. W konsekwencji pociąga to za sobą fakt, że prawdopodobieństwo aposteriori, że przykład X zostanie zaliczony do klasy C2 również wynosi 0. Rozwiązaniem problemu jest dodanie 1 do licznika wystąpień każdej pary <wartość atrybutu – klasa> (estymator Laplace’a).

Podsumowując prezentację naiwnego klasyfikatora Bayes’a, założenie o niezależności atrybutów znacznie redukuje koszt obliczeń. Dodatkowo, jeżeli założenie jest spełnione, naiwny klasyfikator Bayes’a jest optymalny, tzn. zapewnia najlepszą dokładność klasyfikacji w porównaniu z innymi klasyfikatorami. Założenie to jest bardzo rzadko spełnione w praktyce, jednakże naiwny klasyfikator Bayes’a jest zadziwiająco dokładny w porównaniu z innymi metodami klasyfikacji.

Przejdziemy obecnie do przedstawienia ostatniej grupy metod klasyfikacji, mianowicie klasyfikatorów kNN. Klasyfikator kNN tzw. k-najbliższych sąsiadów należy do grupy algorytmów opartych o analizę przypadku. Algorytmy te prezentują swoją wiedzę o świecie w postaci zbioru przypadków lub doświadczeń. Idea klasyfikacji polega na metodach wyszukiwania tych zgromadzonych przypadków, które mogą one być zastosowane do klasyfikacji nowych sytuacji. Klasyfikacja nowych przypadków zgodnie z algorytmem kNN jest realizowana na bieżąco, tzn. wtedy gdy pojawia się potrzeba klasyfikacji nowego przypadku. Algorytm kNN nie buduje klasyfikatora. Załóżmy, że pojedynczy przykład ze zbioru treningowego jest n-wymiarowym wektorem, reprezentującym punkt w przestrzeni n-wymiarowej, którą będziemy nazywać w dalszej części wykładu przestrzenią wzorców.

Rozpocznijmy prezentację tej grupy algorytmów od prezentacji najprostszego algorytmu 1NN. Zgodnie z tym algorytmem klasyfikacja nowego przypadku X realizowana jest w następujący sposób: poszukiwaniu punktu w przestrzeni wzorców, który jest „najbliższy” nowemu przypadkowi. Następnie przypadek X klasyfikujemy jako należący do klasy, do której należy „najbliższy” punkt w przestrzeni wzorców. Łatwo zauważyć, że zasadniczą wadą metody 1NN jest jej czułość na punkty osobliwe i szum w danych treningowych.

Rozwiązaniem problemu klasyfikatora 1NN jest zastosowanie strategii k-najbliższych sąsiadów. Klasyfikacja nowego przypadku X jest realizowana w następujący sposób: Poszukujemy k najbliższych punktów w przestrzeni wzorców. Przypadek X klasyfikujemy jako należący do klasy, która dominuje w zbiorze k najbliższych sąsiadów. Do znalezienia k najbliższych sąsiadów najczęściej wykorzystujemy indeksy wielowymiarowe (np. R-drzewa) itp.

Dwa zasadnicze problemy związane z klasyfikatorem kNN są następujące. Pierwszym z nich jest problem definicji funkcji odległości – jak zdefiniować punkt „najbliższy” nowemu przykładowi X? Drugi problem jest problemem transformacji, w którym pojawia się pytanie ‘Jak przetransformować przykład do punktu w przestrzeni wzorców?’ W odpowiedzi na pierwszy problem, w przypadku atrybutów liczbowych opisujących zbiór treningowy, klasyfikatory kNN stosują najczęściej euklidesową miarę odległości. Możemy zastąpić euklidesową miarę odległości innymi miarami odległości np. miarą blokową (Manhattan) czy też Minkowskiego.

Przyjrzyjmy się drugiemu z wymienionych problemów, mianowicie problemowi transformacji. Zauważmy, że różne atrybuty mogą posiadać różną skalę, różne jednostki, oraz co jest szczególnie istotne, różne przedziały zmienności. Stąd też bezpośrednie zastosowanie funkcji odległości może spowodować dominację pewnych atrybutów nad pozostałymi co spowoduje zapewne zafałszowanie wyniku. Rozwiązaniem w tym wypadku będzie nadanie wag atrybutom lub normalizacja wartości atrybutów, bądź też standaryzacja.

Jak już wspomnieliśmy klasyfikator kNN jest czuły na występowanie punktów osobliwych i zaszumione dane. Stąd też, aby uniknąć zafałszowania wyniku klasyfikacji stosuje się normalizację bądź standaryzację atrybutów. Tradycyjne rozwiązanie standaryzacji polega na tym, że od wartości każdego atrybutu odejmujemy średnią dzielimy przez odchylenie standardowe. To przeprowadza zmienne o różnych jednostkach do zmiennych niemianowanych. Istnieje również szereg zaproponowanych transformacji niestandardowych, do których możemy zaliczyć estymator Donoho-Stahel.

Na zakończenie wykładu wróćmy do problemu dokładności klasyfikatora. Przypomnijmy, że jednym z kryteriów wyboru metody klasyfikacji jest dokładność klasyfikatora. Dokładność klasyfikatora badamy na danym zbiorze testowym. Dokładności klasyfikatora definiujemy jako procent przykładów testowych poprawnie zaklasyfikowanych przez klasyfikator. Pamiętajmy, że dokładności klasyfikatora nie testujemy na zbiorze treningowym! Przeprowadzenie klasyfikacji na zbiorze treningowym pokazałoby 100% dokładność klasyfikatora, jednak wynik ten nie wniósłby nam żadnej interesującej informacji dotyczącej dokładności i jakości klasyfikatora. Mamy tu do czynienia ze zjawiskiem przetrenowania klasyfikatora, oznaczającym że szacunkowa dokładność klasyfikatora na danych treningowych jesr zbyt optymistyczne, stąd, zafałszowane.

Należy przypuszczać, że klasyfikator będzie prawdopodobnie mniej dokładny na niezależnym zbiorze danych aniżeli na zbiorze, na którym został wytrenowany. Do oszacowania dokładności klasyfikatora stosujemy niezależny (od zbioru treningowego) zbiór danych – zbiór testowy. W praktyce istnieje wiele metod szacowania dokładności klasyfikatora. Wybór metody zależy od liczności zbioru treningowego i od liczności zbioru testowego.

W przypadku gdy dysponujemy zbiorem przykładów o dużej liczności stosujemy prosta metodę podziału zbioru na dwa niezależne zbiory: treningowy (70% przykładów) i testowy (30% przykładów). Zbiory treningowy i testowy powinny być reprezentatywne, co oznacza iż rozkład występowania klas w obu zbiorach powinien odpowiadać rozkładowi występowania klas w zbiorze początkowym przykładów. (ang. stratification procedure )

Prezentowany slajd przedstawia zasadę podziału zbioru dostępnych przykładów pomiędzy zbiór testowy i zbiór treningowy. 70% przykładów wykorzystujemy do konstrukcji drzewa. Pozostałe 30% włączamy do zbioru testowego i wykorzystujemy do weryfikacji dokładności otrzymanego klasyfikatora.

Niestety, nie zawsze dysponujemy dużym zbiorem przykładów. W przypadku zbioru przykładów o małej liczności stosujemy najczęściej metodę k-krotnej walidacji krzyżowej (tzw. kroswalidacji). Idea jest następująca: Początkowy zbiór przykładów jest losowo dzielony na k możliwie równych, wzajemnie niezależnych części S1, S2, ..., Sk. Zbiór treningowy stanowi k-1 części, k-ta cześć stanowi zbiór testowy. Sam klasyfikator konstruujemy k-krotnie. W ten sposób otrzymujemy k-klasyfikatorów.

Zauważmy, że każda z k części, po zakończeniu, będzie użyta k-1 razy do konstrukcji drzewa i 1 raz do testowania dokładności klasyfikacji. Sumaryczna liczba błędów klasyfikacji dla wszystkich k klasyfikatorów, podzielona przez liczność n oryginalnego zbioru przykładów daje kroswalidacyjne oszacowanie dokonania błędnej klasyfikacji przez dany klasyfikator. Ostatecznie zostaje wybrany ten klasyfikator, który zapewnia największą dokładność klasyfikacji.

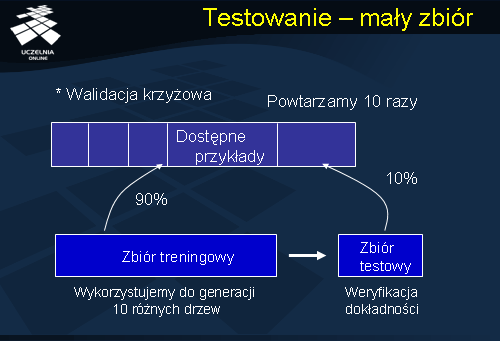
Prezentowany slajd ilustruje działanie metody k-krotnej walidacji krzyżowej (kroswalidacji). Początkowy zbiór przykładów dzielimy na k możliwie równych wzajemnie niezależnych części. Następnie k-1 części stanowi zbiór treningowy, k-ta część (10% dostępnych przykładów) stanowi zbiór testowy. W oparciu o zbiór treningowy konstruujemy klasyfikator. Następnie ponownie wybieramy k-1 części stanowiących zbiór treningowy, pozostała k-ta część stanowi zbiór testowy. Ponownie ze zbioru treningowego konstruujemy klasyfikator i weryfikujemy jego dokładność w oparciu o zbiór testowy. Konstrukcję klasyfikatora powtarzamy 10-krotnie.

Następnie, po wybraniu klasyfikatora, który zapewniał największą dokładność klasyfikacji konstruuje się raz jeszcze klasyfikator w oparciu o cały dostępny zbiór przykładów. W praktycznych zastosowaniach k wynosi najczęściej 10 lub 5. Inne popularne metody szacowania dokładności klasyfikatora, w przypadku, gdy dysponujemy mało licznym zbiorem przykładów to tzw. n-krotna walidacja krzyżowa (ang. leave-one-out cross-validation) lub też wielokrotne repróbkowanie (ang. bootstrapping). Idea n-krotnej walidacji krzyżowej, gdzie n oznacza liczność zbioru przykładów, jest następująca: zbiór testowy składa się z jednego przykładu, pozostałe przykłady służą do konstrukcji klasyfikatora. Wynik n-testów dla każdego przykładu jest uśredniany i stanowi oszacowanie dokonania błędnej klasyfikacji przez klasyfikator. Metoda ta nosi nazwę n-krotnej walidacji krzyżowej, ponieważ klasyfikator konstruujemy n-razy, za każdym razem wybierając do zbioru testowego inny przykład.

Druga z metod polega na wielokrotnym repróbkowaniu (losowanie ze zwracaniem) przykładów z oryginalnego zbioru przykładów. Oryginalny zbiór jest próbkowany n razy (n - liczność zbioru przykładów) tworząc zbiór treningowy o liczności n. Ponieważ jest to losowanie ze zwracaniem, niektóre przykłady będą się powtarzać w zbiorze treningowym, to oznacza, że inne przykłady w tym zbiorze nie wystąpią (dokładnie 0.368% przykładów nie zostanie wylosowanych). Te przykłady utworzą zbiór testowy, który wykorzystujemy do oceny dokładności otrzymanego klasyfikatora. Obie wspomniane metody szacowania klasyfikatora, są bardzo ciekawe i mają największe zastosowanie w przypadku zbioru o małej liczności. Jednakże, podstawową metodą szacowania dokładności klasyfikatora, pozostaje, jest metoda 10-krotnej walidacji krzyżowej.