Wiele naturalnych problemów algorytmicznych to problemy optymalizacyjne, np:
- maksymalny przepływ Dana jest sieć przepływowa. Znaleźć przepływ o maksymalnej wartości.
- problem plecakowy Dane jest \(n\) przedmiotów o wartościach \(v_1,\ldots,v_n\) i rozmiarach \(s_1,\ldots,s_n\) oraz rozmiar plecaka \(B\). Które przedmioty należy włożyć do plecaka aby miały one sumarycznie największą możliwą wartość?
- minimalne pokrycie wierzchołkowe Dany graf nieskierowany \(G=(V,E)\). Znaleźć najmniejsze pokrycie wierzchołkowe \(G\), tzn. podzbiór wierzchołków \(S\), który dotyka każdej krawędzi.
- problem komiwojażera Dany pełny graf \(n\)-wierzchołkowy z nieujemnymi wagami na krawędziach. Znaleźć cykl Hamiltona o najmniejszej wadze (tzn. sumie wag krawędzi).
W problemach tych dla danego egzemplarza problemu (sieć przepływowa, wartości i rozmiary przedmiotów wraz z wielkością plecaka, graf nieskierowany, tablica \({n \choose 2}\) liczb) jest określony pewien zbiór rozwiązań dopuszczalnych (przepływ, wybór przedmiotów mieszczących się w plecaku, pokrycie wierzchołkowe, cykl Hamiltona). Interesuje nas jednak nie dowolne rozwiązanie dopuszczalne ale rozwiązanie w jakimś sensie najlepsze. Dokładniej, na zbiorze rozwiązań dopuszczalnych mamy określoną pewną funkcję celu (o wartościach nieujemnych) i szukamy rozwiązania dopuszczalnego, dla którego wartość funkcji celu (wartość przepływu, sumaryczna wartość przedmiotów w plecaku, liczba wierzchołków w pokryciu, waga cyklu Hamiltona) jest optymalna (maksymalna dla dwóch pierwszych problemów, minimalna dla dwóch pozostałych). Wartość funkcji celu będziemy nazywać krótko kosztem rozwiązania (choć słowo to pasuje przede wszystkim do problemów minimalizacyjnych, w przypadku maksymalizacji lepszym słowem byłaby wartość).
Z wcześniejszych wykładów wiemy, że problem maksymalnego przepływu można rozwiązać efektywnie, tj. w czasie wielomianowym. Jest to jednak sytuacja dość wyjątkowa: większość naturalnych problemów optymalizacyjnych jest NP-trudnych (dokładniej: NP-trudne są ich wersje decyzyjne). Jest tak np. w przypadku trzech ostatnich problemów z powyższej listy. Zamiast bezradnie rozkładać ręce, możemy jednak spytać co można w takiej sytuacji zrobić. Dotąd rozważaliśmy jedynie rozwiązania szybkie (wielomianowe), optymalne i działające dla dowolnych danych. Możemy pójść na kompromis i ograniczyć jedno (lub więcej) z tych wymagań. Współczesna algorytmika w przeważającej części zajmuje się badaniem efektów takich właśnie kompromisów. W tym wykładzie zajmiemy się prawdopodobnie najszerzej badaną wersją: rezygnujemy jedynie z optymalności rozwiązania. Mimo to, będziemy chcieli kontrolować jakość rozwiązań dopuszczalnych zwracanych przez nasze algorytmy. Będą nas interesowały wyniki typu "algorytm zawsze zwraca rozwiązanie gorsze od optymalnego o nie więcej niż 50%". Podamy teraz formalną definicję.
Definicja
Rozważmy wielomianowy algorytm, który dla każdego egzemplarza \(I\) pewnego problemu minimalizacyjnego zwraca rozwiązanie dopuszczalne o koszcie \({\rm ALG}(I)\). Niech \({\rm OPT}(I)\) oznacza koszt optymalnego rozwiązania dla egzemplarza \(I\). Powiemy, że taki algorytm jest \(\alpha\)-aproksymacyjny, gdy dla każdego egzemplarza \(I\),
\[\frac{{\rm ALG}(I)}{{\rm OPT}(I)} \le \alpha.\]
Dla problemów maksymalizacji definicja jest analogiczna, zmienia się jedynie znak nierówności:
\[\frac{{\rm ALG}(I)}{{\rm OPT}(I)} \ge \alpha.\]
Liczba \(\alpha\) jest nazywana współczynnikiem aproksymacji lub ilorazem aproksymacji. Zauważmy w szczególności, że w problemach minimalizacji \(\alpha \ge 1\), natomiast w problemach maksymalizacji \(\alpha \in [0,1]\). Czasem rozszerzamy powyższą definicję tak, że współczynnik aproksymacji \(\alpha\) nie jest stałą tylko pewną funkcją, z reguły zależną od rozmiaru danych: rozważane są np. algorytmy \(\log n
\)-aproksymacyjne czy \(\sqrt{n}\)-aproksymacyjne.
W dalszych rozważaniach będziemy pisać krótko \({\rm OPT}\) zamiast \({\rm OPT}(I)\), gdyż z reguły będzie jasne z kontekstu o jaki egzemplarz problemu chodzi.
2-aproksymacyjny algorytm dla problemu minimalnego pokrycia wierzchołkowego
Podamy teraz bardzo prosty algorytm aproksymacyjny, jednak nawet na tym elementarnym przykładzie widoczne będą pewne cechy obecne w bardziej zaawansowanych algorytmach. Przypomnijmy, że pokryciem wierzchołkowym nieskierowanego grafu \(G=(V,E)\) nazywamy dowolny zbiór wierzchołków \(S \subseteq V\) taki, że dla każdej krawędzi \(uv\in E\) zachodzi \(\{u,v\} \cap S \neq \emptyset\). Zajmiemy się następującym, klasycznym problemem.
Nasz algorytm będzie następujący:
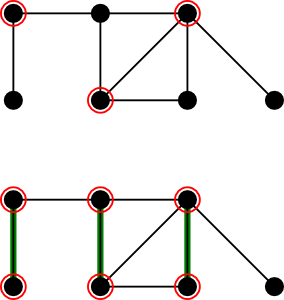Przykład: optymalne pokrycie i pokrycie wygenerowane przez algorytm
Zauważmy, że w punkcie 1. wymagane jest jedynie skojarzenie maksymalne ze względu na zawieranie, a nie najliczniejsze skojarzenie. Takie skojarzenie łatwo jest znaleźć algorytmem zachłannym w czasie liniowym (po prostu dopóki istnieje krawędź, której oba końce nie są skojarzone, dodajemy ją do skojarzenia). Cały algorytm działa więc w czasie liniowym.
Twierdzenie 1 Powyższy algorytm jest poprawnym 2-aproksymacyjnym algorytmem dla problemu pokrycia wierzchołkowego
Dowód
Oznaczmy przez \(C\) zbiór wierzchołków zwracany przez algorytm. Najpierw pokażemy, że \(C\) jest pokryciem. Istotnie, gdyby istniała krawędź \(uv\) taka, że \(\{u,v\}\cap C = \emptyset\), oznaczałoby to, że ani \(u\) ani \(v\) nie jest skojarzony, a więc \(M \cup \{uv\}\) byłoby skojarzeniem zawierającym \(M\), a to jest niemożliwe.
Teraz zajmiemy się współczynnikiem aproksymacji. Rozważmy dowolne pokrycie wierzchołkowe \(S\). Ponieważ każda krawędź skojarzenia musi mieć koniec w pokryciu, a z definicji skojarzenia te końce są parami różne więc \(|S| \ge |M|\). W szczególności jest to prawda dla pokrycia optymalnego, zatem:
\[{\rm OPT} \ge |M|.\]
Ponieważ \(|C|=2|M|\), więc \(|C| \le 2 {\rm OPT}\), co kończy dowód. ♦
Zastanówmy się przez chwilę co tak naprawdę wydarzyło się w naszym algorytmie. Pojawia się tam trzech bohaterów: \(C\) -- czyli rozwiązanie zwrócone przez algorytm, \({\rm OPT}\) -- rozwiązanie optymalne (tu i w dalszej części wykładu używamy tego samego oznaczenia dla pewnego rozwiązania optymalnego i jego kosztu), oraz \(M\) -- skojarzenie maksymalne znalezione przez algorytm. Zastanówmy się jaka jest rola tego ostatniego bohatera, który pojawił się w naszej historii dość niespodziewanie. Skojarzenie \(M\) ma dwie kluczowe cechy: możemy je znaleźć w czasie wielomianowym oraz daje oszacowanie dolne na \({\rm OPT}\): w tym przypadku oszacowanie \({\rm OPT} \ge |M|\). Otrzymujemy więc obiekt, który w sensie naszej miary kosztu rozwiązania (mocy zbioru) jest lepszy niż \({\rm OPT}\) , ale nie jest rozwiązaniem dopuszczalnym. W punkcie 2. algorytmu przekształcamy ten obiekt w rozwiązanie dopuszczalne, tracąc przy tym (dwukrotnie) na koszcie. Skoro nasze rozwiązanie \(C\) jest dwukrotnie gorsze niż \(M\), a \(M\) było lepsze niż \({\rm OPT}\), to \(C\) jest co najwyżej 2 razy gorsze niż \({\rm OPT}\).
Skojarzenie \(M\) jest tu swego rodzaju pośrednikiem między rozwiązaniem \(C\) a \({\rm OPT}\): umiemy porównać \(C\) z \(M\) oraz \(M\) z \({\rm OPT}\), razem dostajemy oszacowanie na \(C\) względem \({\rm OPT}\). Często projektując algorytm aproksymacyjny zaczynamy od wskazania takiego właśnie pośrednika, a następnie zastanawiamy się, jak z jego pomocą zbudować rozwiązanie dopuszczalne, tracąc możliwie mało na koszcie. Ten schemat pojawi się w kilku kolejnych przykładach.
Problem komiwojażera i trudność aproksymacji
W poprzednim przykładzie stosunkowo łatwo dostaliśmy algorytm aproksymacyjny ze współczynnikiem aproksymacji ograniczonym przez niewielką stałą (2). Pojawia się naturalne pytanie: czy jest to możliwe dla każdego problemu optymalizacyjnego (powiedzmy, takiego, którego wersja decyzyjna jest w klasie NP)? Oczywiście nie pokażemy tu twierdzenia w rodzaju "dla problemu X nie istnieje algorytm 10-aproksymacyjny", gdyż implikowałoby to, że \({\rm P}\ne {\rm NP}\), a jak wiemy jest to słynny problem otwarty. Podobnie, nie jesteśmy w stanie udowodnić że problem SAT nie posiada algorytmu wielomianowego. Zamiast tego, dowodzi się, że SAT jest NP-trudny. Zrobimy dokładnie tak samo: pokażemy, że aproksymacja pewnego problemu jest NP-trudna (tzn. gdybyśmy potrafili aproksymować, to rozwiązalibyśmy w czasie wielomianowym wszystkie problemy z NP). Rozważymy tu słynny problem komiwojażera.
Przez \(n\) będziemy oznaczać liczbę wierzchołków grafu \(G\).
Twierdzenie 2
Dla dowolnej funkcji \(\alpha : \mathbb{N}\rightarrow \mathbb{N}\) obliczalnej w czasie wielomianowym (np. \(\alpha(n)=100\), \(\alpha(n)=\log n\), \(\alpha(n)=n^5\), \(\alpha(n)=2^n\), ale \(\alpha(n)=2^{2^n}\) już nie), nie istnieje algorytm \(\alpha(n)\)-aproksymacyjny dla problemu komiwojażera, o ile \({\rm P}\ne {\rm NP}\).
Dowód
Załóżmy, że algorytm o którym mowa istnieje (nazwijmy go ,,algorytm \(A\)''). Pokażemy, że \(A\) mógłby zostać użyty do rozwiązania problemu cyklu Hamiltona w czasie wielomianowym. W problemie cyklu Hamiltona na wejściu pojawia się graf nieskierowany \(G=(V,E)\). Zbudujemy na tej podstawie egzemplarz problemu komiwojażera: będzie to graf pełny \(G'\) o zbiorze wierzchołków \(V\). Pozostaje określić funkcję \(w\):
\[ w(uv) = \left\{ \begin{array}{ll} 1& \mbox{gdy } uv \in E \\ n\cdot\alpha(n) & \mbox{w p. p. }\end{array} \right. \]
Zauważmy, że funkcję \(w\) możemy reprezentować w pamięci wielomianowej względem rozmiaru \(G\). Na tak określonym egzemplarzu uruchamiamy algorytm \(A\).
Wówczas, jeśli \(G\) ma cykl Hamiltona to w naszym egzemplarzu problemu komiwojażera \({\rm OPT} = n\), a więc \(A\) zwróci rozwiązanie o koszcie co najwyżej \(\alpha(n) \cdot n\). Jeśli natomiast \(G\) nie zawiera cyklu Hamiltona to każdy cykl Hamiltona w \(G'\) zawiera krawędź o wadze \(n\cdot\alpha(n)\), a więc cały taki cykl ma wagę większą niż \(n\cdot\alpha(n)\), czyli \(A\) zwróci rozwiązanie o koszcie większym niż \(n\cdot\alpha(n)\).
Powyżej udowodniliśmy, że \(G\) ma cykl Hamiltona wtedy i tylko wtedy gdy \(A\) zwróci rozwiązanie o koszcie co najwyżej \(\alpha(n) \cdot n\), a to możemy sprawdzić w czasie wielomianowym. Ponieważ problem cyklu Hamiltona jest NP-zupełny, więc \({\rm P}= {\rm NP}\), sprzeczność z założeniem. ♦
Metryczny problem komiwojażera: 2-aproksymacja
Pokazując trudność problemu komiwojażera, nie zakładaliśmy niczego o funkcji wagowej \(w\). Tymczasem w wielu zastosowaniach, w szczególności np. jeśli myślimy o podróżowaniu komiwojażera między "prawdziwymi" miastami na powierzchni ziemi, funkcja \(w\) spełnia nierówność trójkąta, tzn. dla dowolnej trójki wierzchołków \(a\), \(b\), \(c\), mamy
\[w(ab) \le w(ac) + w(cb).\]
Rozważymy teraz wariant problemu komiwojażera, w którym zakładamy, że \(w\) spełnia nierówność trójkąta (innymi słowy \(w\), określona na parach wierzchołków zamiast na krawędziach, jest metryką).
Łatwo sprawdzić, że funkcja skonstruowana w dowodzie twierdzenia 2 nie jest metryką, a więc dla takich egzemplarzy nie wykluczyliśmy algorytmów aproksymacyjnych. Okazuje się, że stosunkowo prosto można otrzymać 2-aproksymację. W algorytmie będziemy korzystali z następującego, dobrze znanego, twierdzenia. (Dowód możemy znaleźć np. w wykładzie z matematyki dyskretnej; czytelnik może sprawdzić, że algorytm wynikający z dowodu można zaimplementować w czasie liniowym.)
Twierdzenie
W spójnym multigrafie istnieje cykl Eulera wtedy i tylko wtedy, gdy stopień każdego wierzchołka jest parzysty. Co więcej, jeśli cykl Eulera istnieje, można go znaleźć w czasie liniowym.
Przypomnijmy, że algorytm Kruskala w naszym grafie zadziała w czasie \(O(|E(G)| \log |E(G)|) = O(n^2 \log n)\), natomiast cykl Eulera można znaleźć w czasie liniowym. Całkowita złożoność algorytmu wynosi więc \(O(n^2 \log n)\), a więc jest wielomianowa.
Twierdzenie Powyższy algorytm jest 2-aproksymacyjny.
Dowód W ostatnim kroku algorytmu wypisywana jest pewna permutacja wierzchołków. Ponieważ \(G\) jest grafem pełnym, więc ta permutacja wyznacza kolejne wierzchołki pewnego cyklu Hamiltona \(C\) w \(G\), a więc algorytm zawsze zwraca rozwiązanie dopuszczalne.
Rozważmy dowolne rozwiązanie optymalne OPT. Jest to cykl Hamiltona, a więc w szczególności spójny podgraf rozpinający grafu \(G\) (podgraf rozpinający grafu \(G\) to taki, który zawiera wszystkie wierzchołki \(G\)). Nie jest więc lżejszy niż najlżejszy spójny podgraf rozpinający (który musi być drzewem), a więc:
\[w(T) \le OPT.\]
Stąd \(w(\mathcal{E})=w(T_2)=2w(T) \le 2OPT\). Nasz algorytm dzieli \(\mathcal{E}\) na krawędziowo rozłączne marszruty, o końcach w kolejnych wypisywanych w ostatnim kroku wierzchołkach. Każdej takiej marszrucie \(v_{i_1}\ldots v_{i_j}\) odpowiada krawędź \(v_{i_1}v_{i_j}\) w zwracanym w ostatnim kroku algorytmu cyklu Hamiltona \(C\). Z nierówności trójkąta \(w(v_{i_1} v_{i_j}) \le \sum_{k=1}^{j-1}w(v_{i_k} v_{i_{k+1}})\), więc \(w(C) \le w(\mathcal{E}) \le 2OPT \).♦
Zauważmy, że w tym algorytmie, podobnie jak to miało miejsce w przypadku pokrycia wierzchołkowego, korzystaliśmy z pośrednika: tym razem było to minimalne drzewo rozpinające. Jest to dość naturalny i często używany sposób uzyskiwania pośredników, zwany relaksacją (rozluźnieniem). Chodzi o to, że rozluźniamy warunki dotyczące poszukiwanego obiektu tak, aby uzyskać problem wielomianowy. W tym przypadku szukamy najlżejszego cyklu Hamiltona, natomiast cykle Hamiltona są szczególnym przypadkiem spójnych grafów rozpinających oraz najlżejszy spójny podgraf rozpinający możemy znaleźć w czasie wielomianowym. Oczywiście jeśli warunki są rozluźnione, to minimalny (względem naszego kosztu) obiekt w szerszym zbiorze będzie miał koszt mniejszy lub równy kosztowi rozwiązania optymalnego oryginalnego problemu: dostaniemy więc obiekt lepszy niż OPT, który następnie (tracąc na koszcie) możemy próbować przekształcić do rozwiązania dopuszczalnego.
Metryczny problem komiwojażera: (3/2)-aproksymacja
Okazuje się, że zaprezentowany powyżej algorytm 2-aproksymacyjny można stosunkowo łatwo poprawić. Zmodyfikujemy jedynie jeden jego fragment: krok 2. Zauważmy, że celem kroku 2 jest dodanie krawędzi do drzewa rozpinającego \(T\) tak, aby otrzymać graf, w którym wszystkie wierzchołki mają parzyste stopnie. Dodatkowo chcemy, żeby waga dodanych krawędzi była niewielka. Poprzednio, podwajaliśmy stopień każdego wierzchołka w \(T\). Tym razem spróbujmy być bardziej oszczędni: pozostawmy wierzchołki, które już mają parzysty stopień bez zmian. Niech \(N\) będzie zbiorem wierzchołków nieparzystego stopnia w drzewie \(T\). Przypomnijmy treść lematu o uściskach dłoni:
\[\sum_{v\in V}\deg(v) = 2|E|.\]
Stąd, stosując powyższą równość do drzewa \(T\), widzimy, że \(|N|\) jest parzyste. Wystarczy więc połączyć wierzchołki zbioru \(N\) w pary, i dla każdej pary dodać do \(T\) łączącą je krawędź. Dodatkowo, chcemy to zrobić najtaniej jak się da: innymi słowy, chcemy znaleźć najlżejsze skojarzenie doskonałe (tzn. łączące wszystkie wierzchołki) w podgrafie grafu \(G\) indukowanym przez zbiór \(N\): taki podgraf oznaczamy przez \(G[N]\). Z pomocą przychodzi nam następujące twierdzenie (w wykładzie o przepływach udowodniliśmy je w wersji dla grafów dwudzielnych).
Twierdzenie (Edmonds 1965)
Skojarzenie doskonałe o najmniejszym koszcie można znaleźć w czasie wielomianowym.
W takim razie, krok 2. algorytmu zastępujemy przez:
Pozostaje jeszcze pokazać, że skojarzenie \(M\) ma małą wagę względem wagi rozwiązania optymalnego problemu komiwojażera.
Lemat
Niech \(G=(V,E)\) będzie grafem pełnym z funkcją wagową \(w:E\rightarrow\mathbb{R}\) spełniającą nierówność trójkąta. Niech \(X\) będzie dowolnym podzbiorem \(V\) o parzystej mocy oraz niech \(M\) będzie najlżejszym skojarzeniem doskonałym w grafie \(G[X]\). Jeśli \({\rm OPT}\) jest najlżejszym cyklem Hamiltona w \(G\), to
\[w(M) \le \frac{1}{2} w({\rm OPT}).\]
Dowód
Niech \({\rm OPT}_X\) będzie dowolnym najlżejszym cyklem Hamiltona w \(G[X]\). Ponieważ \({\rm OPT}_X\) ma parzystą długość, więc jest sumą dwóch rozłącznych skojarzeń \({\rm OPT}_X = M_1 \cup M_2\). Stąd \(w({\rm OPT}_X) = w(M_1) + w(M_2) \ge 2 w(M)\), czyli (*)
\[w(M) \le \frac{1}{2}w({\rm OPT}_X).\]
Rozważmy teraz cykl Hamiltona \(C=e_1\ldots e_{|X|}\) w \(G[X]\), w którym wierzchołki zbioru \(X\) odwiedzane są w takiej samej kolejności jak w cyklu \({\rm OPT}\). Cykl Hamiltona \({\rm OPT}\) możemy podzielić na rozłączne ścieżki \({\rm OPT}=p_1p_2\ldots p_{|X|}\) tak, że dla każdego \(i=1,\ldots,|X|\) ścieżka \(p_i\) łączy końce krawędzi \(e_i\). Z nierówności trójkąta łatwo pokazać, że \(w(e_i) \le w(p_i)\). Stąd,
\[w({\rm OPT})=\sum_{i=1}^{|X|}w(p_i) \ge \sum_{i=1}^{|X|}w(e_i) = w(C) \ge w({\rm OPT}_X),\]
gdzie ostatnia nierówność wynika z tego, że \({\rm OPT}_X\) jest najlżejszym cyklem Hamiltona w \(G[X]\). Otrzymaliśmy więc \(w({\rm OPT}_X)\le w({\rm OPT})\), co razem z (*) daje tezę.
♦
Na podstawie powyższego lematu otrzymujemy, że \(w(T_2) = w(T) + w(M) \le w({\rm OPT}) + \frac{1}{2}w({\rm OPT}) = \frac{3}{2}w({\rm OPT})\). Jeśli dokończymy analizę tak jak w przypadku algorytmu 2-aproksymacyjnego, dostaniemy poniższe twierdzenie.
Twierdzenie (Christofides 1976)
Istnieje algorytm (3/2)-aproksymacyjny dla metrycznego problemu komiwojażera.
Warto zaznaczyć, że do dziś (2011r) nie jest znany algorytm o mniejszym współczynniku aproksymacji i stworzenie takiego algorytmu jest jednym z najważniejszych problemów otwartych w dziedzinie algorytmów aproksymacyjnych. W 2010r. udało się uzyskać lepsze algorytmy (aktualny rekord to 13/9=1,(4)) dla szczególnego przypadku, gdy \(w\) jest metryką najkrótszych ścieżek w nieskierowanym grafie bez wag.