Informatyka MIMUW

Definicje, oznaczenia i podstawowe własności

---

Przyjmijmy, że \(\mathbb{N}=\left\{ 1,2,\ldots \right\}\) oznacza zbiór liczb naturalnych, a \(\mathbb{N}_{0}\) zbiór liczb naturalnych wraz z 0. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie.

Definicja 1.1

Zbiór \(S\), w którym określone jest działanie łączne, to znaczy spełniające warunek

\(\forall x,y,z \in S \;\;\; x\cdot (y\cdot z)=(x\cdot y)\cdot z\)

nazywamy półgrupą.

Przykład 1.1

Zbiór liczb naturalnych z dodawaniem \((\mathbb{N},+)\) tworzy półgrupę.

Definicja 1.2

Półgrupę \(M\), w której istnieje element neutralny działania, to znaczy element \(1_{M}\in M\) spełniający warunek

\(\forall x\in M \;\;\;1_M \cdot x=x\cdot 1_M=x\)

nazywamy monoidem.

Przykład 1.2

(1) Zbiór liczb naturalnych z mnożeniem \((\mathbb{N},\cdot ,1)\) jest monoidem.

(2) Zbiór liczb naturalnych z zerem \((\mathbb{N}_{0},+,0)\) jest monoidem ze względu na dodawanie.

(3) Monoidem jest \((A^A,\circ,id_A)\) - zbiór odwzorowań dowolnego zbioru \({A}\) w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym.

Dwa pierwsze monoidy są przemienne, czyli działanie jest przemienne, a trzeci jest nieprzemienny.

Każdy monoid jest półgrupą.

Dla uproszczenia notacji będziemy opuszczać kropkę "\(\cdot\)" oznaczającą działanie oraz używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to \((\mathbf{S},\cdot )\) będzie oznaczać półgrupę, a \((\mathbf{M},\cdot ,\, 1_{\mathbf{M}})\) monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn \(x_1...x_n,\) a także \(x^n=x...x\) (n razy) jest określony jednoznacznie bez potrzeby wprowadzania nawiasów. Dla dowolnych liczb naturalnych \(m,n\in \mathbb{N}\) zachodzą wzory

\(\begin{array} {c} x^{m+n}=x^{m}x^{n}=x^{n}x^{m},\\ (x^{m})^{n}=x^{mn}. \end{array}\)

Dla dowolnego \(x \in M\) przyjmujemy z definicji

\(x^0 = 1_{M}.\)

Strukturę monoidu \(M\) przenosimy na zbiór potęgowy \(\mathcal{P}(M)\) wszystkich podzbiorów monoidu \(M\), określając dla dowolnych \(A,B \in\mathcal{P}(M)\) działanie

\(A\cdot B=\left\{ x\in {\bf M}\: :\: \exists a\in A,\: \exists b\in B\: ,\: x=ab\right\}\)

\((\mathcal{P}(M),\cdot, \{1_{M}\})\) jest monoidem.
Podobnie przenosimy strukturę półgrupy z \(S\) na \(\mathcal{P}(S)\).
Dla dowolnego podzbioru monoidu (półgrupy) i dla dowolnej liczby \(n \in \mathbb{N}\) zapis \(A^n\) oznacza n-krotny iloczyn zbioru \({A}\) przez siebie rozumiany w powyższym sensie.
W szczególności \(A^{1}=A.\)

W przypadku monoidu przyjmujemy z definicji

\(A^0 = \{ 1_{ M} \}.\)

Definicja 1.3

Homomorfizmem półgrup \((S,\cdot)\;,\;\;(S',*)\) nazywamy odwzorowanie

\(h~:S~\longmapsto~S'\) takie, że

\(\forall x,y \in S \;\;\; h(x\cdot y)=h(x)*h(y).\)

Homomorfizmem monoidów \((M,\cdot,1_{M}),\;(M',*,1_{M'})\) nazywamy odwzorowanie \(h:M \longmapsto M'\)

takie, że

\(\forall x,y \in {M} \;\;\;h(x\cdot y)=h(x)*h(y) \;\;\; i \;\;\; h(1_{M})= 1_{M'}.\)

Przykład 1.3

Odwzorowanie \(h:{\mathbb{Z}}_{mod\, 3}\longrightarrow {\mathbb{Z}}_{mod\,6}\) takie, że

\(\begin{array} {c} \begin{array} {l} 1\longrightarrow 4\\ 0\longrightarrow 0\\ 2\longrightarrow 2 \end{array} \end{array}\)

jest homomorfizmem półgrupy \((\mathbb{Z}_{mod\,3},\cdot )\) w półgrupę \((\mathbb{Z}_{mod\,6},\cdot )\), ale nie jest homomorfizmem monoidu \((\mathbb{Z}_{mod\,3},\cdot,1 )\) w monoid \((\mathbb{Z}_{mod\,6},\cdot,1 )\), bo wartością 1 z monoidu \((\mathbb{Z}_{mod\,3},\cdot, 1 )\) nie jest jedynka monoidu \((\mathbb{Z}_{mod\,6},\cdot,1 )\).

Definicja 1.4.

Niech \((S,\cdot),\;\;(M,\cdot,1_{M})\) będą odpowiednio dowolną półgrupą, monoidem.

• \((T,\cdot)\) nazywamy podpółgrupą \({S}\) wtedy i tylko wtedy, gdy \(T\subset S\) i \(T^2 \subset T.\)

• \((N,\cdot,1_{M})\) nazywamy podmonoidem \(M\) wtedy i tylko wtedy, gdy \(N\) jest podpółgrupą \(M\) i \(1_{M} \in N.\)

Przykład 1.4.

\((\mathbb{Z}_{mod\,6},\cdot )\) jest monoidem. Podzbiór \(\{2,4\}\), jako zamknięty na działanie \(\cdot _{mod\, 6}\), tworzy podpółgrupę \(\mathbb{Z}_{mod\, 6}\). \((\{2,4\},\cdot _{mod\, 6})\) jest monoidem z \(4\) jako elementem neutralnym, ale nie podmonoidem \(\mathbb{Z}_{mod\, 6}\).

Niech \(X\) będzie dowolnym podzbiorem monoidu \(M\). Zbiór

\(X^*= \{1\}\cup X\cup X^2\cup ...\cup X^n \cup \ldots = \bigcup_{i=0}^\infty X^i\)

jest podmonoidem monoidu \(M\). Jest to najmniejszy, w sensie inkluzji podmonoid monoidu \(M\) zawierający zbiór \(X\). Gdy spełniona jest równość \(X^*={M}\), to mówimy, że \(X\) jest zbiorem generatorów monoidu \(M\). Zachodzą następujące własności:

1. Zbiór generatorów nie jest wyznaczony jednoznacznie.

2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór \({M}\).

Podobnie dla dowolnego podzbioru \(X\) półgrupy \({S}\) zbiór

\(X^+=X\cup X^2\cup...\cup X^n \cup \ldots = \bigcup_{i=1}^\infty X^i\)

jest podpółgrupą \({S}\) i to najmniejszą w sensie inkluzji zawierającą zbiór \(X\).
Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup.

Przykład 1.5.

W monoidzie \((\mathbb{N}_{0},+,0)\) podmonoid generowany przez zbiór generatorów \(X=\{2\}\) składa się z liczb parzystych i nieujemnych.

Definicja 1.5

Niech \(S\) będzie półgrupą. Relację równoważności \(\rho \subset {S}^2\) nazywamy:

(1) prawą kongruencją w półgrupie \({S}\), jeśli

\(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow xz\;\rho\; yz,\)

(2) lewą kongruencją w półgrupie \({S}\), jeśli

\(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy,\)

(3) kongruencją, jeśli jest prawą i lewą kongruencją, tzn.

\(\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy \;\; i \;\; xz\;\rho\; yz.\)

Zastępując w powyższej definicji półgrupę \(S\) na monoid \(M\) otrzymamy dualnie pojęcia prawej kongruencji, lewej kongruencji i kongruencji zdefiniowane w monoidzie.
Mając kongruencję \(\rho\) określoną w półgrupie \({S}\) (monoidzie \(M)\) możemy utworzyć półgrupę ilorazową \({S}/\rho\) (monoid ilorazowy \({M}/\rho\)), której elementami są klasy równoważności (abstrakcji) relacji \(\rho\).

Dla dowolnego homomorfizmu półgrup \(h:{S}\longmapsto {S}'\) określamy relację

\(Ker_h = \{ (x,y)\in {S}\times {S}\;:\;\; h(x)=h(y) \}.\)
Relacja \(Ker_h\) jest kongruencją w półgrupie \({S}.\)

Dla homomorfizmu monoidów \(h:{M}\longmapsto {M}'\) relacja \(Ker_h\) jest kongruencją w monoidzie \(M\).

Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać.

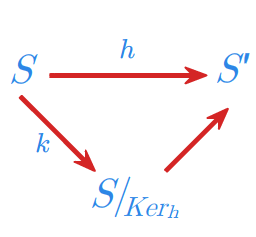
Twierdzenie 1.1

Niech \(h:{S}\longmapsto {S}'\) będzie dowolnym epimorfizmem półgrupy \({S}\) na półgrupę \({S}'.\) Półgrupa \({S}'\) jest izomorficzna z półgrupą ilorazową \({S}/_{Ker_h}\).

Rysunek 1

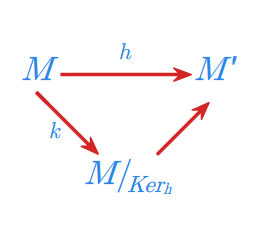
Twierdzenie 1.2

Niech \(h:{M}\longmapsto {M}'\) będzie dowolnym epimorfizmem monoidu \({M}\) na monoid \({M}'.\) Monoid \({M}'\) jest izomorficzny z monoidem ilorazowym \({M}/_{Ker_h}\).

Rysunek 2

Półgrupy wolne i monoidy wolne

Niech \({A}\) oznacza dowolny zbiór.

Definicja 2.1

Wolnym monoidem \(A^*\) o bazie \({A}\) nazywamy zbiór wszystkich skończonych ciągów:

\(A^*=\{ (a_1,...,a_n)\;\;:\;\;n \geq 0\;\;,\;\;a_i \in A \}\) wraz z działaniem \((a_1,...,a_n)\cdot (b_1,...,b_m) = (a_1,...,a_n,b_1,...,b_m).\)

Ciąg pusty \({(n=0)}\) oznaczamy symbolem "1" i z definicji jest on elementem neutralnym określonego powyżej działania, nazywanego katenacją lub konkatenacją.

Przyjmujemy następującą konwencję zapisu: W oparciu o nią możemy stwierdzić inkluzję \(A\subset A^*\).

Ta inkluzja uzasadnia użycie wprowadzonego wcześniej oznaczenia \(A^*\).
\(A^*\) jest najmniejszym podmonoidem monoidu \(A^*\) zawierającym \(A.\)

Definicja 2.2

Wolną półgrupą \(A^+\) nad alfabetem \(A\) nazywamy zbiór wszystkich skończonych ciągów:

\(A^+=\{ (a_1,...,a_n)\;\;:\;\;n > 0,\;\;\;a_i \in A \}\)

wraz z działaniem katenacji.

Używa się także określeń - wolny monoid o bazie \(A\) i wolna półgrupa o bazie \(A\).

• Elementy alfabetu \({A}\) nazywamy literami.

• Elementy wolnego monoidu (półgrupy) nazywamy słowami i oznaczać bedziemy w wykładzie najczęściej literami \(u,v,w\).

• Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy językiem.

Długością słowa \(w \in A^*\) nazywamy liczbę \(|w|\) będącą długością ciągu określającego to słowo. Słowo puste 1, czyli odpowiadające ciągowi pustemu ma długość równą 0.

Przykład 2.1

(1) Wolna półgrupa \(\{0,1\}^+\) składa się z ciągów binarnych.

(2) Wolny monoid \(\{0,1\}^*\) składa się z ciągów binarnych i ciągu pustego.

Definicja 2.3

Niech \(A\) i \(B\) będą alfabetami. Podstawieniem nazywamy homomorfizm

\(s:A^{*}\longrightarrow \mathcal{P}(B^{*}).\) Odwzorowanie \(s\) jako homomorfizm monoidu \(A^{*}\) w monoid \(\mathcal{P}(B^{*})\) spełnia dla dowolnych \(v,w\in A^{*}\) równość \(s(vw)=s(v)s(w) \;\; \text{oraz}\;\; s(1)=\{1\}.\)

Twierdzenie 2.1.

Niech \({A}\) oznacza dowolny zbiór, a \(({M},\cdot,1_{M})\) dowolny monoid.

(1) Każde odwzorowanie

\(f:A\longmapsto {M}\)

daje się jednoznacznie rozszerzyć do homomorfizmu \(h:A^*\longmapsto {M}.\)

(2) Homomorfizm \({h}\) jest epimorfizmem wtedy i tylko wtedy, gdy \(f(A)\) jest zbiorem generatorów \({M}.\)

Dowód

(1) Przyjmujemy

\(\forall\; a_1...a_n \in A^+\;\;\;\;h(a_1...a_n)=f(a_1)...f(a_n) \;\;\;\text{oraz}\; \;\;h(1)=1_{M}.\)

Tak określone \(h\) jest jedynym rozszerzeniem przekształcenia \(f\).

(2) \(f(A)^*=M \Leftrightarrow \forall s \in {M}\;\; s=f(a_1)...f(a_n)=h(a_1...a_n)\) dla pewnego \(a_1...a_n \in A^*\Leftrightarrow h\) jest suriekcją.

Przyjmując w powyższym twierdzeniu jako \(A\) dowolny zbiór generatorów monoidu \({M}\) oraz jako funkcję \(f\) włożenie \(id_{A}:A\longrightarrow \mathbf{M}\) równe identyczności na \({A}\) dochodzimy do następującego wniosku.

Wniosek 2.1.

Każdy monoid \({M}\) jest homomorficznym obrazem wolnego monoidu \(A^*\) utworzonego nad dowolnym zbiorem generatorów \({M}.\)

Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.
Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup).

Twierdzenie 2.2.

Monoid \({M}\) jest wolny wtedy i tylko wtedy, gdy każdy element \(m \in {S}={M}\setminus \{1\}\) ma jednoznaczny rozkład na elementy zbioru \(A={S}\setminus {S}^2.\)

Dowod

Załóżmy, że monoid \({M}\) jest wolny, to znaczy \({M}=B^*\) dla pewnego zbioru (bazy) \(B.\)

• Udowodnimy, że \(A{}\) jest zbiorem generatorów monoidu \(M\). W tym celu wykażemy, że zachodzi inkluzja
  \({S}\subset ({S}\setminus {S}^2)^+.\)
  Dowód przeprowadzimy nie wprost. Załóżmy więc, że

\({S}\setminus ({S}\setminus {S}^2)^+ \neq \emptyset\)

i niech \({m}\) oznacza element z tego zbioru o najmniejszej długości w \(B^*.\)
Wnioskujemy stąd kolejno:

\(m\notin ({S}\setminus {S}^2)^+\)
\(m\in {S}^2\)
\(m=s_1s_2\) dla pewnych \(s_1,s_2\in {S}\),

przy czym długość \(s_1,s_2\) jest silnie mniejsza niż długość \(m.\) Zatem

\(s_1,s_2 \in ({S}\setminus {S}^2)^+\)

a to oznacza, że

\(m=s_1s_2 \in ({S}\setminus {S}^2)^+.\)

Otrzymana sprzeczność kończy dowód faktu, że \(A={S}\setminus {S}^2\) jest zbiorem generatorów monoidu \({M}.\)

• Pokażemy teraz, że \(A \subset B.\)
  Niech \(m=b_1...b_k \in {S}\setminus {S}^2\) dla pewnych \(b_i \in B\), \(i=1,...,k.\)
  Jeśli \(k>1\), to \(m\in {S}^2\), co jest sprzeczne z wyborem \(m.\) Zatem \({k=1}\), co implikuje \(A\subset B.\)

Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy \(B\), a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru \(A={S}\setminus {S}^2.\)

Niech teraz \({M}\) oznacza monoid z jednoznacznością rozkładu na elementy zbioru \(A~=~S~\setminus~S^2\). Rozszerzamy identyczność \(id_A:A\longmapsto {M}\) do homomorfizmu \(h:A^*\longmapsto {M}.\) Z założenia wynika, że każdy element \(m \in {S}\) można przedstawić jako iloczyn

\(m=a_1...a_n \;\;\; gdzie \;\;\;a_i \in A \;\;\; dla \;\;\; i=1,...,n.\)

Zatem

\(h(a_1...a_n)=h(a_1)...h(a_n) a_1...a_n.\)

Homomorfizm \(h\) jest izomorfizmem, więc monoid \({M}\) jako izomorficzny z \(A^*\) jest wolny.

Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup.

Twierdzenie 2.3.

Półgrupa \({S}\) jest wolna wtedy i tylko wtedy, gdy każdy element \(x \in {S}\) ma jednoznaczny rozkład na elementy zbioru \({S}\setminus {S}^2.\)

Wniosek 2.2.

Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów.

Przyklad 2.2.

(1) Półgrupa \((\mathbb{N},+ )\) jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - \(\mathbb{N}\setminus (\mathbb{N}+\mathbb{N})=\left\{ 1\right\}\).

(2) Dla \(\mathbb{N}_2=\{n \in \mathbb{N}:n\geq 2\}\) półgrupa \((\mathbb{N}_2,+ )\) nie jest to półgrupą wolną.
Nie ma jednoznaczności rozkładu na elementy z \(\mathbb{N}_2\setminus (\mathbb{N}_2+\mathbb{N}_2)=\{2,3\}\).
Na przykład \(6=2+2+2=3+3\).