W sortowaniu przez scalanie dzieliliśmy sortowany ciąg na dwa mniejsze (o równych lub prawie równych rozmiarach), rekurencyjnie sortowaliśmy mniejsze podciągi, a na koniec scalaliśmy posortowane podciągi w jeden. Metodą algorytmiczną zastosowaną w tym algorytmie jest
dziel i zwyciężaj. Z tej metody można także skorzystać w inny sposób. Przypuśćmy, że chcemy posortować \( n \)-elementowy zbiór \( X \). Jeżeli \( X \) składa się tylko z jednego elementu, to nic nie trzeba robić. W przeciwnym razie wybieramy dowolny element \( x_0 \) z \( X \), a następnie dzielimy \( X \) na trzy zbiory: \( X_1 = \{x \in X: x \le x_0\} \), \( \{x_0\} \), \( X_2 = \{x\in X: x \ge x_0 \} \).
Zauważmy, że nawet gdy \( X \) jest multizbiorem, to każdy ze zbiorów \( X_1, X_2 \) ma mniej elementów niż \( X \). Może oczywiście zdarzyć się, że jeden z tych zbiorów jest pusty. Jeśli teraz rekurencyjnie posortujemy \( X_1 \) i \( X_2 \), a następnie wypiszemy najpierw elementy \( X_1 \), potem \( x_0 \), a na koniec elementy \( X_2 \), dostaniemy uporządkowany ciąg elementów zbioru \( X \). Pomysł powyższego algorytmu pochodzi od Hoare'a.
Zanim przedstawimy wydajną implementację tego algorytmu, zanalizujemy jego złożoność w przedstawionej wersji rekurencyjnej. Zajmiemy się liczbą porównań. Liczba przemieszczeń elementów będzie zależała od konkretnej implementacji. Ile porównań jest nam potrzebnych do dokonania podziału zbioru \( X \)? Niewątpliwie \( n-1 \) - każdy z elementów z \( X-\{x_0\} \) porównujemy z \( x_0 \). (Uwaga: przy implementacji przedstawionej poniżej liczba porównań wyniesie w pesymistycznym przypadku \( n+1 \). Nie ma to jednak wpływu na asymptotyczną złożoność algorytmu, jak i nawet na stałą przy dominującym składniku funkcji złożoności.) Działanie algorytmu można przedstawić za pomocą drzewa binarnego, w którego węzłach zapisano elementy wykorzystywane w podziałach stosownych zbiorów. W korzeniu drzewa znajduje się element dzielący cały zbiór \( X \). W korzeniu lewego poddrzewa - element dzielący podzbiór \( X_1 \), a w korzeniu prawego poddrzewa - element dzielący podzbiór \( X_2 \), itd. Jeśli zbiór składa się tylko z jednego elementu, oczywiście żadnego podziału nie dokonujemy, a jedyny element takiego zbioru jest w liściu drzewa. Porządek elementów w całym zbiorze \( X \) wyznaczamy przechodząc drzewo działania algorytmu w porządku infiksowym.
Ćwiczenie 7
Uzasadnij, że na \( i \)-tym poziomie drzewa wykonujemy nie więcej niż \( n-i-1 \) porównań.
Maksymalna wysokość drzewa wynosi \( n-1 \). Zatem w pesymistycznym przypadku wykonujemy \( n-1 + n-2 + \ldots + 1 = \frac{n(n-1)}{2} \) porównań.
Ćwiczenie 8
Załóżmy, że porządkujemy zbiór \( X = \{1,2, \ldots, n\} \). Ile jest różnych drzew o wysokości \( n-1 \) odpowiadających wykonaniom naszego algorytmu?
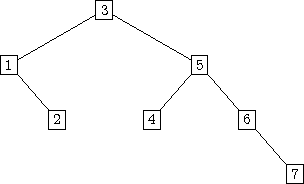
Rys. Przykładowe drzewo wykonania dla \( X=\{1,\ldots,7\} \)
Odpowiedzmy sobie teraz na pytanie, kiedy wykonamy najmniejszą liczbę porównań. Jeśli wysokość drzewa wynosi \( h \), wykonamy ich nie więcej niż \( h(n-1) \). Zatem najlepszym jest drzewo o jak najmniejszej wysokości, na przykład zupełne drzewo binarne, lub drzewo, w którym elementy zbioru \( X \) są rozmieszczone w następujący sposób:
w korzeniu znajduje się element "środkowy" (\( \lfloor \frac{n}{2} \rfloor \) co do wielkości licząc od najmniejszego); w korzeniu lewego poddrzewa element "środkowy" ze zbioru \( X_1 \); w korzeniu prawego poddrzewa element "środkowy" ze zbioru \( X_2 \); itd.
Wysokość takiego poddrzewa wynosi \( \lfloor \log n \rfloor \). Zatem w tym przypadku liczba porównań nie przekroczy \( n\log n \). To jest tyle, ile w sortowaniu przez scalanie. Zauważmy, że żeby wysokość drzewa obliczeń była logarytmiczna, elementy dzielące nie muszą być "środkowymi" w swoich zbiorach. Wystarczy zagwarantować, żeby rozmiary zbiorów otrzymywanych w wyniku podziału były o stały czynnik mniejsze od rozmiaru zbioru dzielonego. Na przykład, gdybyśmy chcieli tylko, żeby rozmiary dzielonych zbiorów wynosiły co najwyżej \( \frac{3}{4} \) rozmiaru dzielonego zbioru, wystarczy za element dzielący wybierać dowolny z elementów, który ma w dzielonym zbiorze co najmniej \( \frac{1}{4} \) elementów mniejszych i co najmniej \( \frac{1}{4} \) elementów większych. Zatem w takim przypadku dobrzy kandydaci na element dzielący stanowią połowę wszystkich elementów dzielonego zbioru. Innymi słowy, gdy element dzielący wybieramy losowo, to z prawdopodobieństwem \( \frac{1}{2} \) trafiamy na "dobry" element. To jest właśnie idea algorytmu szybkiego sortowania, znanego powszechnie pod angielską nazwą QuickSort. Jeżeli element dzielący będziemy wybierać losowo, jest duża szansa na to, że sortowanie zajmie \( O(n\log n) \) porównań. Spróbujmy teraz formalnie zanalizować liczbę porównań wykonywanych przez nasz algorytm, przy założeniu, że za element dzielący bierzemy losowy element ze zbioru \( X \), przy czym zakładamy, że każdy element może zostać wybrany z jednakowym prawdopodobieństwem \( \frac{1}{|X|} \). Dodatkowo bez straty ogólności załóżmy, że \( X = \{1,2,\ldots, n\} \). (Uwaga: to założenie nie byłoby uprawnione, gdyby \( X \) był multizbiorem.) Niech \( Y_{i,j} \) będzie zmienną losową przyjmującą wartość 1, gdy \( i \) jest porównywane z \( j \) podczas sortowania, oraz 0 w przeciwnym przypadku, dla każdych \( 1\le i < j \le n \). Jeśli przez \( Y \) oznaczymy zmienną losową, której wartością jest liczba porównań wykonywanych w algorytmie, to \( Y = \sum_{1\le i < j \le n}Y_{i,j} \). Z liniowości wartości oczekiwanej wiemy, że \( E[Y] = \sum_{1\le i < j \le n}E[Y_{i,j}] \). Zauważmy, że \( E[Y_{i,j}] = p_{i,j} \), gdzie \( p_{i,j} \) jest prawdopodobieństwem tego, że \( i \) jest porównywane z \( j \), dla każdych \( 1\le i < j \le n \). Ile wynosi \( p_{i,j} \)? Żeby obliczyć to prawdopodobieństwo, ustalmy pewne obliczenie dla zbioru \( X = \{1,2,\ldots, n\} \) i niech \( T \) będzie drzewem tego obliczenia. Rozważmy permutację \( p = < p_1, p_2, ..., p_n> \) liczb \( 1,2,\ldots, n \) występujących w węzłach tego drzewa, przy przeglądaniu jego węzłów poziomami od strony lewej do prawej, poczynając od korzenia.
Na podstawie permutacji \( p \) łatwo sprawdzić, czy dwa elementy \( 1 < i < j \) są porównywane w sortowaniu odpowiadającym \( p \).
Obserwacja
Elementy \( i, j \), \( 1\le i < j \le n \) są porównywane w sortowaniu definiowanym przez \( p \) wtedy i tylko wtedy, gdy w permutacji \( p \) jeden z elementów \( i, j \) występuje przed wszystkimi elementami \( i+1, i+2, \ldots, j-1 \).
Ćwiczenie 9
Uzasadnij powyższą obserwację.
Obserwacja pozwala łatwo policzyć prawdopodobieństwo \( p_{i,j} \) - prawdopodobieństwo porównania \( i,j \) podczas sortowania. Ponieważ \( i,j \) są ze sobą porównywane tylko wtedy, gdy \( i \) lub \( j \) pojawi się jako pierwsze spośród \( i,i+1, \ldots, j \), a wybór każdego elementu jako elementu dzielącego jest jednakowo prawdopodobny, to \( p_{i,j} = \frac{2}{j-i+1} \). Stąd mamy \( E[Y_{i,j}] = \frac{2}{j-i+1} \), i dalej
\( E[Y] = \sum_{1\le i < j \le n} \frac{2}{j-i+1} = \)
\( \sum_{i = 1}^{n-1} \sum_{j= i+1}^n \frac{2}{j-i+1} = 2 \sum_{i = 1}^{n-1}(\frac{1}{2} + \frac{1}{3} + \ldots \frac{1}{n-i+1}) = \)
\( 2\sum_{i = 1}^{n-1}(H_{n-i+1} - 1) = \)
\( 2\sum_{i = 2}^n(H_i - 1) = 2\sum_{i = 1}^n H_i -2n +1 \),
gdzie \( H_k \) jest \( k \)-tą liczbą harmoniczną. Wynika stąd, że oczekiwana liczba porównań w randomizowanym algorytmie \( QuickSort \) wynosi \( \frac{2}{\log e}n\log n + O(n) \). Współczynnik przy \( n\log n \) wynosi w przybliżeniu 1.4.
Zajmiemy się teraz nierandomizowaną wersją algorytmu \( QuickSort \). Tak jak dotychczas naszym celem jest posortowanie tablicy \( a[1..n] \). Bez straty ogólności przyjmijmy, że dany jest strażnik \( a[n+1] \) o wartości nie mniejszej od największego elementu w tablicy \( a \). Tak jak w wersji randomizowanej podstawą algorytmu jest podział danego (multi-) zbioru elementów względem wybranego elementu tego zbioru. Będziemy zakładali, że elementy dzielonego zbioru składają się na podtablicę \( a[l..r] \), dla pewnych \( 1\le l < r \le n \). Za element dzielący będziemy brali \( a[l] \). Niech \( v = a[l] \). Naszym celem będzie takie przemieszczenie elementów podtablicy \( a[l..r] \), żeby zaszły następujące warunki:
\( a[j] = v \), dla pewnego \( l\le j \le r \),
\( a[i] \le v \), dla każdego \( i = l, l+1, \ldots, j-1 \),
\( a[i] \ge v \), dla każdego \( i = j+1, j+2, \ldots, r \).
Jednym słowem, jeśli elementami dzielonego zbioru \( X \) są elementy z podtablicy \( a[l..r] \), to w wyniku podziału dostajemy \( X_1 = \{a[l],a[l+1],\ldots, a[j-1]\} \) oraz \( X_2 = \{a[j+1],a[j+2],\ldots, a[r]\} \).
Podziału \( a[l..r] \) dokonujemy za pomocą funkcji \( Partition(l,r) \), której wartością będzie docelowa pozycja \( v=a[l] \).
Algorytm Podział
Partition(l,r)::
begin
v := a[l]; i := l; j := r+1;
repeat
//Niezmiennik: dla każdego k=l,l+1,...,i a[k] <= v,
// dla każdego k=j,j+1,...,r+1, a[k] => v,
// j-i => -1.
repeat i := i+1 until a[i] => v;
repeat j := j-1 until a[j] <= v;
if i < j then
Exchange(i,j);
until i => j;
a[l] := a[j]; a[j]:= v;
return j
end;
Zauważmy, że procedura \( Partition \) wykonuje co najwyżej \( j-i+2 \) porównania. To jest co najwyżej o 2 więcej niż w przypadku, gdy każdy element dzielonego zbioru (poza elementem dzielącym) jest porównywany z elementem dzielącym.
Mając w ręku procedurę podziału łatwo już zrealizować sortowanie podtablicy \( a[l..r] \). Dokonamy tego za pomocą rekurencyjnej procedury \( QS(l,r) \).
Algorytm QuickSort - wersja rekurencyjna
QS(l,r)::
begin
if (r - l) > 1 then
begin
j := Partition(l,r);
QS(l,j-1);
QS(j+1,r)
end
end;
Żeby posortować całą tablicę \( a \), wystarczy wywołać \( QS(1,n) \).
W tak zapisanym szybkim sortowaniu nie mamy randomizacji i niestety złe dane będziemy zawsze sortować w czasie kwadratowym. Jeśli jednak dane są losowe, nasz algorytm będzie miał takie same walory jak algorytm randomizacyjny. Zauważmy, że jeśli w tablicy \( a \) zapisano losową permutację (przyjmujemy, że każda permutacja jest jednakowo prawdopodobna), to \( a[1] = k \) z prawdopodobieństwem \( \frac{1}{n} \), dla każdego \( k = 1,2,\ldots,n \). Więcej, można pokazać, że w wyniku podziału względem \( v = a[1] \), elementy podtablicy \( a[1..j-1] \) tworzą losową permutację (każda permutacja tych elementów jest jednakowo prawdopodobna), jak i elementy podtablicy \( a[j+1..r] \) tworzą losową permutację. Wynika stąd, że w przypadku losowych danych algorytm \( QS \) zachowuje się tak, jak algorytm randomizowany, a oczekiwana liczba porównań jest taka sama, z dokładnością do składnika mniejszego rzędu. Liczba przemieszczeń elementów nigdy nie przekroczy liczby wykonywanych porównań.
Nietrudno powyższy algorytm przerobić na algorytm randomizowany. Wystarczy tylko na samym początku procedury Partition wylosować indeks \( k \) z przedziału \( l, l+1, \ldots, r \) i zamienić elementy \( a[l] \) i \( a[k] \).
Niski współczynnik przy \( n\log n \) (1.4) tłumaczy, dlaczego ten algorytm nazywamy szybkim. Zauważmy, że sortowanie przez scalanie wymagało dodatkowej tablicy i dużej liczby przemieszczeń elementów. W sortowaniu kopcowym współczynnik przy \( n\log n \) wynosił 2.
Rekurencyjna wersja szybkiego sortowania ma jeszcze jedną, ukrytą wadę. Potrzebna jest dodatkowa pamięć na stos służący do realizacji rekursji. Niestety w pesymistycznym przypadku rozmiar stosu może być liniowy ze względu na \( n \). Szczęśliwie oba wywołania rekurencyjne są na końcu procedury QS i jedno z nich łatwo zamienić na iterację, a na stos można odkładać tylko parametry drugiego wywołania. Ponieważ mamy dwa wywołania, możemy sami podjąć decyzję, które z nich wykonywać iteracyjnie, a parametry którego odkładać na stos. Naszym celem jest ograniczenie rozmiaru stosu. Nietrudno zauważyć, że na stos należy odkładać parametry większego przedziału. Ponieważ w iteracji będziemy przetwarzali przedział o rozmiarze co najmniej połowę mniejszym od rozmiaru przedziału dzielonego, to liczba przedziałów aktualnie znajdujących się na stosie nigdy nie przekroczy \( \log n \). Dokładną analizę rozmiaru stosu pozostawiamy jako ćwiczenie. Zanim jednak do tego przystąpimy, zapiszmy nierekurencyjną wersję algorytmu szybkiego sortowania. W zapisie tej procedury \( S \) jest stosem na który odkładamy parametry \( l,r \) przedziału do posortowania. Operacja \( Push(S,l,r) \) oznacza włożenie pary \( (l,r) \) na stos \( S \), natomiast operacja \( Pop(S,l,r) \) oznacza pobranie i usunięcie końców przedziału z wierzchołka stosu \( S \) i zapisanie ich w zmiennych \( l,r \). Funkcja \( Empty(S) \) służy do sprawdzania, czy stos jest pusty. Jeśli \( S \) jest pusty, to \( Empty \) przyjmuje wartość PRAWDA, w przeciwnym razie \( Empty \) przyjmuje wartość FAŁSZ. Oto nierekurencyjna wersja szybkiego sortowania.
Algorytm QuickSort - wersja nierekurencyjna
begin
zainicjuj stos S z jedną parą (1,n) ; //sortujemy tablicę a[1..n]
repeat
Pop(S,l,r); //pobranie parametrów kolejnej podtablicy do sortowania
//chcemy posortować a[l..r]
while l < r do //dopóki sortowana podtablica ma co najmniej
//2 elementy
begin
j:= partition(l,r); //dzielimy a[l..r]
//krótszą podtablicę przetwarzamy iteracyjnie, końce dłuższej
//odkładamy na stos
if (j-l) <= (r-j) then
begin Push(S,j+1,r); r := j-1 end
else
begin Push(S,l,j-1); l := j+1 end
end
until Empty(S)
end;
Ćwiczenie 10
Udowodnij, że wysokość stosu nigdy nie będzie większa niż \( \log n \).