Ćwiczenia | Informatyka MIMUW

Zadanie 1

Podaj przykład ciągu $O(n)$ operacji MakeSet, Find i Union w implementacji listowej bez łączenia z wyważaniem, których łączny koszt to $\Theta(n^2)$ .

Rozwiązanie

Tworzymy n singletonów, a potem kolejno dla

$i = 1, 2 \ldots n-1$ dołączamy listę długości

$i$ za listę długości 1.

Zadanie 2

Udowodnij, że w implementacji listowej z heurystyką łączenia z wyważaniem koszt wykonania $m$ operacji MakeSet, Find i Union, spośród których $n$ to MakeSet, wynosi $O(m+n\log n)$ .

Rozwiązanie

Przez indukcję dowodzimy, że długość listy zawierającej element, który miał

$k$ razy zmieniany wskaźnik do reprezentanta, wynosi co najmniej

$2^k$ . Wynika z tego, że każdy element może mieć zmieniany wskaźnik do reprezentanta co najwyżej

$\log n$ razy, koszt zamortyzowany operacji Union wynosi więc

$O(\log n)$ .

Zadanie 3

Udowodnij, że w implementacji drzewiastej z łączeniem według wysokości wysokość drzewa zawierającego $n$ węzłów jest mniejsza bądź równa $\lfloor\log n\rfloor$ .

Rozwiązanie

Przez indukcję względem

$h$ dowodzimy, że drzewo o wysokości

$h$ musi zawierać co najmniej

$2^h$ węzłów. Wysokość drzewa wzrasta podczas operacji Union wtedy i tylko wtedy, gdy łączymy dwa drzewa takiej samej wysokości.

Zadanie 4

Napisz pseudokod operacji MakeSet, Union i Find w implementacji drzewiastej z łączeniem według rangi i kompresją ścieżki.

Rozwiązanie

MakeSet(x)

ojciec(x) := x

ranga(x) := 0

Union(x,y)

if ranga(x)>ranga(y) then
  ojciec(y) := x
else
   ojciec(x) := y

  if ranga(x) = ranga(y) then
    ranga(y) := ranga(y)+1

Find(x)
if x <> ojciec(x) then
ojciec(x) := Find(ojciec(x))
return ojciec(x)

Zadanie 5

Udowodnij Lemat 1.

Rozwiązanie

Zauważmy, że ranga węzła

$x$ w lesie zbiorów rozłącznych powstającym w wyniku ciągu

$\sigma$ operacji MakeSet, Union i Find jest równa wysokości poddrzewa

$x$ w lesie dla ciągu operacji

$\sigma'$ utworzonego z

$\sigma$ przez usunięcie wszystkich operacji Find. Stąd natychmiast wynikają punkty (a) i (b), bo wysokości poddrzew na ścieżce od dowolnego węzła do korzenia tworzą ciąg ściśle rosnący. Punkt (c) wynika z zadania 3, a (d) wynika z (c) (bo każdy węzeł może należeć do co najwyżej jednego poddrzewa o korzeniu rangi

$r$ ).

Zadanie 6

Udowodnij, że jeśli w implementacji drzewiastej z łączeniem według rangi i kompresją ścieżki najpierw wykonujemy wszystkie operacje Union, a dopiero potem wszystkie operacje Find, to zamortyzowany koszt operacji Find jest stały.

Rozwiązanie

Każdą krawędź drzewa utworzonego w wyniku ciągu operacji Union - z wyjątkiem krawędzi prowadzących do korzenia - przechodzimy tylko raz.

Zadanie 7

Algorytm Kruskala znajdowania minimalnego drzewa rozpinającego w grafie $G = (V,E)$ z wagami na krawędziach działa następująco: krawędzie są przeglądane w kolejności od najlżejszej do najcięższej. Aktualnie rozważaną krawędź dodajemy do budowanego drzewa, o ile tylko nie powoduje to powstania cyklu. Jak efektywnie zaimplementować ten algorytm? Jaki jest jego czas działania?

Rozwiązanie

Sortujemy krawędzie niemalejąco według wag: $e_1, \ldots, e_m$ ;
for i := 1 to |V| do

MakeSet(v_i);
T := $\emptyset$ ;
for j := 1 to m do
niech $e_j = \{v_i, v_k\}$ ;
if Find( $v_i$ ) <> Find( $v_k$ ) then
T := T $\cup \{e_j\}$ ;
Union(Find( $v_i$ ),Find( $v_k$ ))

Koszt tej implementacji jest zdominowany przez koszt sortowania: $O(m\log m)$ .

Zadanie 8

Napisz program generujący labirynt następująca metodą: Na początku każda komnata jest otoczona ścianami. W każdym kroku wybieramy losowo ścianę i usuwamy ją, jeśli komnaty po jej obu stronach nie są jeszcze połączone żadną drogą.

Rozwiązanie

Do zarządzania relacją "komnaty są połączone pewną drogą" należy wykorzystać strukturę danych dla zbiorów rozłącznych.

Zadanie 9

Plansza do gry w Hex ma kształt rombu zbudowanego z sześciokątnych pól. Dwaj gracze wykonują na przemian ruchy polegające na dostawieniu pionka na jedno pole. Celem pierwszego gracza jest zbudowanie z białych pionków drogi łączącej lewy dolny brzeg planszy z prawym górnym, natomiast celem drugiego jest zbudowanie z czarnych pionków drogi łączącej lewy górny brzeg planszy z prawym dolnym.

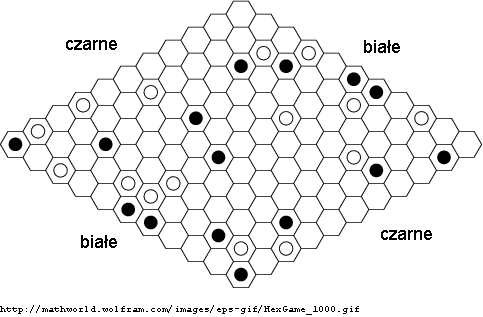
Zaprojektuj algorytm, który po każdym ruchu sprawdza, czy nastąpiła wygrana któregoś z graczy.

Rozwiązanie

Planszę możemy interpretować jako graf, w którym wierzchołki odpowiadają polom, a krawędzie łączą te pola, które sąsiadują ze sobą. Warto dołożyć jeszcze po dwa sztuczne białe i czarne wierzchołki połączone krawędziami z polami z odpowiednich brzegów planszy. Po każdym ruchu algorytm powinien uaktualnić składowe, odpowiednio, w białej albo czarnej części grafu (Union) i sprawdzić, czy sztuczne, "brzegowe" wierzchołki znalazły się w jednej składowej (Find).