Informatyka MIMUW

Niech \( x=a_{1}a_{2}\dots a_{n} \) i niech \( x_{n+1}=\# \) będzie specjalnym znakiem leksykograficznie większym od każdego innego symbolu 9w przyszłości będziemy również używać \( x_{n+1}=\# \) jako najmniejszego symbolu).

Oznaczmy przez \( sufiks_{i}=a_{i}a_{i+1}\dots a_{n} \) sufiks tekstu x zaczynający się na pozycji i-tej.

Niech \( SUF[k] \) będzie pozycją, od której zaczyna się k-ty leksykograficznie sufiks x. Sufiks zaczynający się na pozycji \( (n+1) \)-szej nie jest brany pod uwagę.

Ciąg sufiksów posortowany leksykograficznie wygląda następująco:

\( sufix_{SUF[1]} < sufix_{SUF[2]} < sufix_{SUF[3]} < \ldots sufix_{SUF[n]} \)

Rysunek 1: Tablicą sufiksową tekstu \( x\ =\ babaabababba\# \) jest ciąg \( SUF\ =\ [4,\ 2,\ 5,\ 7,\ 9,\ 12,\ 3,\ 1,\ 6,\ 8,\ 11,\ 10] \)

Oznaczmy przez \( lcp[k] \) długość wspólnego prefiksu \( k \)-tego i następnego sufiksu w kolejności leksykograficznej. Na rysunku wartości najdłuższego wspólnego prefiksu między kolejnymi słowami są przedstawione jako zacienione segmenty. Odpowiadają one tablicy \( lcp\ =\ [1,\ 3,\ 4,\ 2,\ 1,\ 0,\ 2,\ 4,\ 3,\ 2,\ 1] \).
Tablica sufiksowa ma następująca ‘’sympatyczną’’ własność: Niech

\( min_{z}=\min\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \), \( max_{z}=\max\{k : z \mbox{ jest prefiksem } sufiks_{SUF[k]}\} \).

Wtedy \( Occ(z,x) \) jest przedziałem w tablicy sufiksowej od \( min_{z} \) do \( max_{z} \).

Drzewo sufiksowe jest drzewem, w którym każda ścieżka jest etykietowana kolejnymi symbolami pewnego sufiksu, oraz każdy sufiks \( x \) jest obecny w drzewie. Gdy dwie ścieżki się rozjeżdżają, tworzy się wierzchołek. Mówiąc bardziej formalnie, każdej krawędzi jest przypisane jako etykieta pewne podsłowo \( x \). Krawędzie wychodzące z tego samego węzła różnią się pierwszymi symbolami swoich etykiet (patrz rysunek).

Etykiety są kodowane przedziałami w tekście \( x \): para liczb \( [i,j] \) reprezentuje podsłowo \({a}_i a_{i +1_j}\) (zobacz prawe drzewo na rysunku). Dzięki temu reprezentacja ma rozmiar \( O(n) \). Wagą krawędzi jest długość odpowiadającego jej słowa.

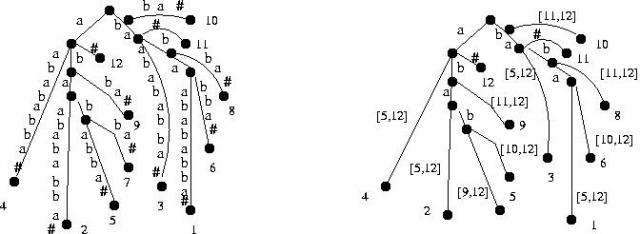
Rysunek 2: Drzewo sufiksowe dla tekstu \( x\ =\ babaabababba \). Na końcu jest dodany znak \( \# \). Końcowe węzły zawierają informację, gdzie zaczyna się sufiks, którym dochodzimy do danego węzła.

Obie reprezentacje pozwalają szybko rozwiązywać problem string-matchingu oraz mają rozmiar liniowy. Niech z będzie wzorcem o długości m, a \( x \) słowem długości n. Z reguły \( m < < n \).