Słownik podsłów bazowych i konstrukcja tablicy sufiksowej w czasie O(n log n)
Opiszemy uproszczoną wersję algorytmu Karpa-Millera-Rosenberga (w skrócie algorytmu KMR) rozwiązywania problemów tekstowych metodą słownika podsłów bazowych. Ustalmy pewnie tekst \( x \) długości \( n \).
Zakładamy w tej sekcji, że dodatkowym symbolem jest \( x_{n+1}=\# \), leksykograficznie najmniejszy symbol. Przez segment \( k \)-bazowy rozumiemy segment tekstu \( x[i..i+2^k-1] \) długości \( 2^k \) lub kończący się na \( x_{n+1} \).
Teoretycznie możemy założyć, że po symbolu \( \# \) mamy bardzo dużo takich symboli na prawo i każdy segment startujący w\( x[1..n] \) ma dokładnie długość \( 2^k \).
Słownik podsłów bazowych (w skrócie DBF(x), od ang. dictionary of basic factors) składa się z \( \log n \) tablic
\( NAZWA_0 \), \( NAZWA_1 \), \( NAZWA_2 \),\( \ldots NAZWA_{\log n} \).
Zakładamy, że \( NAZWA_k[i] \) jest pozycją słowa \( x[i..i+2^k-1] \) na posortowanej liście (bez powtórzeń) wszystkich podsłów długości \( 2^k \) słowa \( x \). Jeśli długość wystaje poza koniec \( x \) to przyjmujemy że są tam (wirtualnie) same symbole \( \# \). Poniżej przedstawiamy przykład słownika podsłów bazowych \( DBF(abaabbaa) \).

Algorytm liczenia tablic Nazwa jest bardzo prosty. Załóżmy od razu, że symbole są ponumerowane leksykograficznie. Wtedy \( NAZWA_0 \) jest zasadniczo równa tekstowi \( x \).
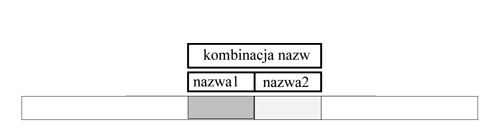
Rysunek6: Słowo rozmiaru \( 2^{k+1} \) otrzymuje najpierw nazwę-kompozycję: kombinacją nazw (będących liczbami naturalnymi z przedziału \( [1..n] \)) dwóch podsłów długości \( 2^k \) .
Opis jednej iteracji \( (transformacja: NAZWA_k\ =>\ NAZWA_{k+1} \))
Dla każdego \( i \) tworzymy nazwę-kompozycję slowa \( x[i..i+2^{k+1}-1] \) jako \( NAZWA_k[i], NAZWA_k[i+2^k] \) Każda taka kompozycja jest parą liczb naturalnych. Sortujemy te pary za pomocą algorytmu radix-sort i w ten sposób otrzymujemy tablicę, która koduje (w porządku leksykograficznym) każdą parę liczbą naturalną (pozycją w porządku leksykograficznym). Wartością \( NAZWA_{k+1}[i] \) jest kod pary \( (NAZWA_k[i],NAZWA_k[i+2^k]) \).
Zauważmy, że tablica sufiksowa odpowiada tablicy \( NAZWA_{\lceil \log n \rceil} \). Możemy to podsumować następująco:
1. słownik DBF(x) możemy skonstruować w czasie \( O(n \log n) \)i pamięci \( O(n \log n) \) (jest to również rozmiar słownika).
2. Tablicę sufiksową możemy otrzymać,stosując algorytm KMR, w czasie \( O(n \log n) \) i pamięci \( O(n) \). (Potrzebujemy pamiętać jedynie ostatnie dwie tablice w każdej iteracji.)