Automaty minimalne | Informatyka MIMUW

Niech $w\in\Sigma^{*}$ będzie słowem o długości $|w|=n>0$ . Dowieść, że minimalny automat deterministyczny rozpoznający wszystkie słowa nad $\Sigma$ , których sufiksem jest $w$ , ma dokładnie $n+1$ stanów.
Niech $w\in\Sigma^{*}$ będzie słowem o długości $|w|=n>0$ . Dowieść, że minimalny automat deterministyczny rozpoznający wszystkie podsłowa słowa $w$ ma nie więcej niż $2n$ stanów.
Narysować diagramy automatów minimalnych rozpoznających odpowiednio
1. wszystkie podsłowa
2. wszystkie sufiksy
słowa $abbababa$ (dla przejrzystości rysunków pominąć stan ,,śmietnik”).
Ile stanów maja analogiczne automaty dla $w_{n}=ab(ba)^{n}$ (licząc stan ,,śmietnik”) ?
Skonstruować minimalny deterministyczny automat skończony dla języka $L\ =\ \{ a^{i}bb^{*}a^{j}\ :\ 2\ |\ (i+j)\}$ .
Skonstruować minimalny deterministyczny automat skończony dla języka
$L\ =\ \{\ a_{1}a_{2}\ldots a_{n}\ :\ n>0,\ a_{i}\in\{ 0,1,2,3,4\},\ MAX_{{i,j}}(a_{i}-a_{j})\le 2\}.$
Opisać strukturę i narysować diagram minimalnego deterministycznego automatu skończonego akceptującego wszystkie skończone ciągi zerojedynkowe takie, że każde k kolejnych symboli zawiera dokładnie 2 jedynki i każde kolejnych j<k symboli zawiera co najwyżej dwie jedynki:
1. Dla $k=3$ ;
2. dla $k=4$ .
(W szczególności słowo puste należy do obu języków, a słowo 111 do żadnego z nich.)
Dowieść, że minimalny automat deterministyczny równoważny podanemu automatowi niedeterministycznemu o n stanach (n≥2) ma dokładnie
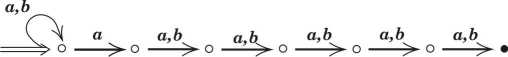
1. $2^{{n-1}}$ stanów,
2. (*)
  
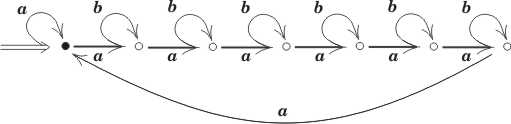
  $2^{n}$ stanów.
Na powyższych rysunkach $n=7$ , stan początkowy jest wskazany przez $\Rightarrow$ , a stan akceptujący jest oznaczony przez $\bullet$ .

Uwaga. Właność słów rozpoznawaną przez automat z punktu można łatwo opisać w języku polskim, w przypadku punktu jest to trudniejsze.
Oznaczmy przez $\Sigma _{k}$ alfabet $\{ 0,1,\ldots k\}$ . Niech $\mathit{NPAL}_{k}$ oznacza zbiór słów nad alfabetem $\Sigma _{k}$ nie zawierających, jako podsłowa, palindromu (symetrycznego słowa długości co najmniej 2). Ile stanów ma minimalny automat deterministyczny akceptujący $\mathit{NPAL}_{{99}}$ ? Podać rozwiązanie ogólne dla $k=0,1,2,\ldots$
Trzy drużyny piłkarskie $A$ , $B$ i $C$ rozgrywają między sobą serię spotkań towarzyskich, przy czym umówiły się, że każdy kolejny mecz jest rozgrywany pomiędzy drużyną, która wygrała poprzedni mecz i drużynę, która nie brała udziału w tym spotkaniu (tzn. jeśli drużyna $X$ wygrała z drużyną $Y$ , to następny mecz rozegrają $X$ i $Z$ ). Zakładając, że nie ma remisów, rozważamy zbiór słów nad alfabetem $\{ A,B,C\}$ , stanowiących ciągi możliwych wyników spotkań. Dowieść, że jest to język regularny. Zbudować minimalny automat deterministyczny, który go rozpoznaje.
Pan $X$ zakupił pakiety trzech różnych akcji: $A,B$ i $C$ . Każdego dnia bada wzajemne położenie wartości swoich akcji, które może być reprezentowane jako uporządkowanie zbioru $\{ A,B,C\}$ , w kierunku od najmniej do najbardziej wartościowej. (Przyjmujemy założenie, że dwie różne akcje mają zawsze różne wartości.) Pan $X$ postanowił, że jeśli w ciągu dwóch kolejnych dni któraś z akcji dwukrotnie spadnie na niższą pozycję, to sprzeda tę akcję. Np. jeśli kolejne notowania (w tym wypadku: uporządkowania) są $(A,B,C),(B,C,A),(C,B,A)$ to pan $X$ sprzeda pakiet akcji $C$ . Rozważamy zbiór $G$ wszystkich uporządkowań liniowych zbioru $\{ A,B,C\}$ . Dowieść, że zbiór tych ciągów nad alfabetem $G$ , które opisują takie wyniki notowań giełdowych, przy których pan $X$ nie pozbędzie się żadnego pakietu akcji, jest językiem regularnym. Znale”zć liczbę stanów automatu minimalnego akceptującego ten język.
Pan $X$ postanowił, że każdego dnia będzie pracował lub nie, przestrzegając przy tym zasady, by na żadne siedem kolejnych dni nie przypadało więcej niż cztery dni pracy. Możliwy rozkład dni pracy pana $X$ w ciągu $n$ kolejnych dni możemy przedstawić jako $n$ -bitowe słowo, gdzie 1 odpowiada dniowi pracy, a 0 dniowi odpoczynku. Dowieść, że zbiór wszystkich tak otrzymanych słów jest językiem regularnym (nad alfabetem $\{ 0,1\}$ ). Znale”zć minimalny automat deterministyczny.
Wskazówka. Jako stany minimalnego automatu weżmy ciągi binarne długości 7 zawierające dokłądnie 4 jedynki,
plus stan typu śmietnik.

Naturalny automat pamięta historie (ciąg binarny) ostatnich siedmiu dni.
Każdy taki ciąg jest równoważny ciągowi dopełnionemu: zamieniamy kolejne zera od lewej na jedynke tak aby w sumie
były 4 jedynki.

Zatem ostatecznie automat ma tyle stanów ile jest ciągów binarnych długości 7 mających 4 jedynki, plus stan smietnik.
W sumie 35+1=36.
Dowieść, że istnieje nieskończenie wiele słów $w\in(a+b)^{*}$ takich, że jeśli zastosujemy homomorfizm $a\mapsto 0$ , $b\mapsto 1$ , to otrzymamy zapis binarny liczby podzielnej przez 3, a kiedy zastosujemy homomorfizm $a\mapsto 1$ , $b\mapsto 0$ , to również otrzymamy zapis binarny liczby podzielnej przez 3 (oczywiście ignorujemy początkowe zera).
Rozważamy automat wydający napoje, działający na następujących zasadach.
— Każdy napój kosztuje 1 złoty.

— W chwili początkowej automat nie zawiera żadnych monet.

— Automat przyjmuje monety: 1 złoty lub 1 euro; w tym ostatnim przypadku wydaje 3 złote reszty po warunkiem, oczywiście, że ma dostateczną ilość monet jednozłotowych (zakładamy, że €1 = 4 zł).

— Jeśli automat nie jest w stanie wydać reszty — sygnalizuje błąd.

— Jeśli po wrzuceniu monety i ewentualnym wydaniu reszty wartość wszystkich monet zgromadzonych w automacie osiągnie równowartość 8 zł, wszystkie monety są wyjmowane (reset).

Historią działania jest ciąg wrzuconych monet (złoty lub euro). Historia jest udana, jeśli w trakcie jej realizacji ani razu nie wystąpił błąd.

Skonstruować minimalny automat deterministyczny rozpoznajacy zbiór wszystkich udanych historii.
Narysować minimalny deterministyczny automat skończony rozpoznający zbiór $L$ słów nad alfabetem $\{ a,b\}$ , zawierający słowo puste oraz słowa rozpoczynające się od $a$ , które nie zawierają jako podsłowa palindromu o długości większej niż 3. (Na rysunku stan “śmietnik” pomijamy.) Jaka jest liczność języka $L$ ?
Narysować minimalny deterministyczny automat skończony rozpoznający język $L_{1}$ składający się ze wszystkich słów binarnych nie zawierających antypalindromu o długości większej niż 2 (zob. zadanie ??.??).
Dla automatu niedet. A przez $det(A)$ oznaczmy deterministyczną wersję $A$ (poprzez konstrukcję ”potęgową”, stanami są zbiory $A$ ) w której są tylko stany osiągalne ze stanu początkowego. Przez $A^{R}$ oznaczmy naturlany automat (z reguly niedeterministyczny) dla odwróconego języka $L(A)^{R}$ (powstały przez odwrócenie strzałek (tranzycji), oraz zamianę zbiorów stanów akceptujących i początkowych).
Prof. J. Brzozowski zauważył, następującą własność

$(*)$ jeśli $A$ jest deterministyczny to $det(A^{R})$ jest minimalnym automatem deterministycznym dla języka $L(A)^{R}$ .

Udowodnić własność $(*)$ .