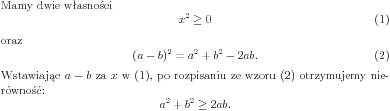Informatyka MIMUW

Wprowadzenie

Co to jest Latex

Latex wywodzi się z Tex'a. Zarówno Tex jak i Latex mają analogiczne przeznaczenie, przy czym Latex jest znacznie wygodniejszy. A zatem czym jest Latex?

Latex służy do wytwarzania przejrzyście wyglądających dokumentów tekstowych takich jak książki, artykuły, czy nawet prezentacje. Docelowym formatem jest wydruk, czy też pliki w różnych formatach, takich jak PDF, Postscript, czy też HTML. Szczególnie wygodne jest tworzenie dokumentów technicznych, matematycznych, ale z powodzeniem może też być stosowany do pisania dokumentacji programów albo zbioru opowiadań.

Latex, podobnie jak języki programowania, ma swój własny język, w którym pisze się treść dokumentu oraz posiada narzędzia (można by powiedzieć "kompilatory"), które przetwarzają pliki źródłowe i generują pliki docelowe. W językach programowania zazwyczaj jedną z istotnych rzeczy jest zbiór bibliotek z gotowymi implementacjami różnych typowych czynności. Również w Latexu jest dużo gotowych pakietów pozwalających w szybki sposób tworzyć najróżniejsze elementy i rodzaje dokumentów.

Filozofia Latexa jest taka, aby skupiać się na tym co merytorycznie ma zawierać dany dokument, a jak najmniej poświęcać uwagi na to, jak ma to wyglądać. Innymi słowy wprowadzamy tylko strukturę i zawartość dokumentu, a latex za nas robi resztę roboty, aby wyjściowy dokument wyglądał jak należy. Oczywiście mamy dużą możliwość ingerencji w wygląd, ale zazwyczaj jest to tylko dobieranie jakiegoś szablonu lub potrzeba uzyskania niestandardowego efektu. Jest to zupełnie inna filozofia, niż w wielu innych edytorach tekstowych, szczególnie w różnych aplikacjach biurowych, gdzie prawie na każdym kroku musimy od decydować, jaki ma być wygląd, wielkość liter, czcionka, odstępy, sposób wyświetlania tytułów itp.

Dystrybucje

Podstawą możliwości cieszenia się twórczością w Latexu jest posiadanie wszystkich narzędzi, pakietów, czcionek, itp. Gotowe zbiory są dostępne w różnych dystrybucjach. Oprócz tych narzędzi, początkujący użytkownicy mogą skorzystać z gotowych środowisk do obrabiania dokumentów Latexu.

Podstawową dystrybucją jest TeX Live. Jest ona dostępna pod wiele różnych platform. Jest łatwą w instalacji kompletną paczką narzędzi, programów, czcionek.

Użytkownicy Linuxa w swoich dystrybucjach zazwyczaj mają dostępny pakiet TeTeX, którego instalacja udostępnia wszelkie niezbędne narzędzia. Pod Linuxem wygodnym środowiskiem graficznym jest Kile.

Dla użytkowników Windowsa jest też bogata dystrybucja ProTeXt oparta na innej dystrybucji MiKTex i ponadto zawierająca kilka wydonych narzędzi, jak na przykład środowisko graficzne TeXnicCenter.

Typowa sesja

Z poziomu linii komand, droga do utworzenia dokumentu wynikowego składa się z wykonania kilku poleceń [pokaż] .

Plikom latexowym nadajemy rozszerzenie tex. Do kompilacji plik latexowego służy polecenie latex:

$ latex dok.tex

Polecenie wyrzuca szereg skomplikowanych napisów, którymi nie należy się przejmować do momentu, gdy nie są to informacje o błędzie w dokumencie.

W wyniku kompilacji powstaje szereg plików. Są to pliki pomocnicze, pliki z logami i najważniejszy plik o rozszerzeniu dvi (ang. device independent). Plik ten można już oglądać w postaci graficznej za pomocą polecenia xdvi:

$ xdvi dok.dvi

Ten format ma swoje ograniczenia, np. nie umożliwia dodawania obrazków, więc nie jest docelowym formatem. Aby utworzyć plik typu PostScript służy polecenie dvips:

$ dvips -o dok.ps dok.dvi

Polecenie to na podstawie pliku dvi tworzy plik ps. Aby obejrzeć ten plik, możemy użyć polecenie gv:

$ gv dok.ps

Możemy też utworzyć plik pdf. Najprostszym sposobem jest kompilacja za pomocą polecenia pdflatex zamiast latex:

$ pdflatex dok.tex

W wyniku powstaje kilka plików, ale najważniejsze jest, że powstaje też plik pdf. Przy tworzeniu w ten sposób plików o formacie pdf są pewne ograniczenia co do zawartości pliku latexowego. Warto mieć tą świadomość, gdy naszym celem jest plik pdf.

Struktura dokumentu

Plik źródłowy jest plikiem tekstowym zawierającym polecenia latexa, właściwą treść i inne symbole kontrolujące zawartość dokumentu. Polecenie latexa jest ciągiem liter (małych i dużych) zaczynającym się od znaku \. Polecenie może mieć argumenty. Argument umieszczany jest pomiędzy klamrami { i }  (ale nie jest to konieczne, gdy argument składa się z jednego znaku; klamry ogólnie służą do grupowania). Argumenty opcjonalne umieszczane są pomiędzy nawiasami kwadratowymi [ i ] .

Plik musi mieć odpowiednią strukturę. Składa się z dwóch części:

1. preambuły i
2. części głównej.

Preambuła powinna zaczynać się od polecenia \documentclass{...} określającego rodzaj dokumentu. Najczęstszym rodzajem jest article. Polecenie też przyjmuje argumenty opcjonalne. Najczęściej używane to

• a4paper - ustawia rozmiar papieru na A4,
• 10pt, 11pt, 12pt - rozmiar tekstu.

Następnie mogą znaleźć się polecenia dotyczące stylu całego dokumentu i deklaracje dodatkowych pakietów. Pakiet dołączamy za pomocą polecenia \usepackage{...}.

Część główna ma postać:

\begin{document}
Treść dokumentu...
\end{document}

A oto przykładowy dokument, który zawiera deklaracje pakietów potrzebnych do obsługi języka polskiego:

% Preambuła
\documentclass[a4paper,11pt]{article}
\usepackage[polish]{babel}
\usepackage[OT4]{fontenc}
\usepackage[utf8]{inputenc}
 
% Część główna
\begin{document}
Treść.
\end{document}

Znak % oznacza komentarz. Po wystąpieniu % wszystkie znaki do końca linii są ignorowane przez kompilator.

Pakiet inputenc mówi, w jaki sposób są wprowadzone w pliku tekstowym znaki międzynarodowe. Współcześnie coraz częściej używa się kodowania UTF-8, które jest użyte w tym przykładzie. Jest ono wspierane już przez większość edytorów. Możemy podać też inne sposoby kodowania, a przykład często spotykany standard ISO-8859-2 (Latin-2). Aby go użyć należy podać latin2 jako argument opcjonalny (zamiast utf8).

Podstawy

Paragrafy

Podstawowym rodzajem treści dokumentu jest tekst, czyli wyrazy, zdania i całe paragrafy.

Sekcje

Dla zwiększenia czytelności powinno dzielić się dokument na części. Podstawowym podziałem są sekcje.

Tytuł

Każdy szanujący się dokument powinien zaczynać się od tytułu, autora i ewentualnie daty powstania. Dlatego na początku części głównej można umieścić następujący kod.

\title{Wprowadzenie do \LaTeX-a} \author{Jan Kowalski} \date{\today} \maketitle

Jak widzimy w tym przykładzie w argumentach poleceń można też używać inne polecenia.

Czcionki

Możemy też zmieniać krój czcionki oraz jego rozmiar.

To \emph{słowo} jest wyróżnione (tak właśnie \LaTeX{} rozumie wyróżnianie słów). \texttt{To zdanie jest napisane czcionką maszynową.} Z kolei to {\sf słowo} i to \textsf{słowo} jest napisane czcionką bezszeryfową. {\Large Ten akapit jest trochę większy. Możemy nadal stosować inne czcionki, np. {\bf pogrubioną} i będą one również powiększone.} W tym akapicie {\small niektóre słowa} są mniejsze. Do tego {\small mogą być napisane {\sc kapitalikami lub być pisane {\it kursywą}}}.

Widzimy, że rozmiar i krój mogą być zagnieżdżone. Nie można zagnieżdżać krojów. Istotny jest zawsze ostatnio wybrany krój. Pełną listę krojów i rozmiarów można znaleźć w dokumentacji latexa.

W powyższym przykładzie używaliśmy symbolów grupowania { i }. Wszystko co występuje pomiędzy tymi symbolami nazywamy grupą. Grupy służą do składania w jeden element większej ilości elementów (np. przy tworzeniu argumentów) albo do ograniczenia zasięgu użytych komend. W tym przykładzie grupy służy nam do ograniczenia zasięgu użytego kroju, czy też rozmiaru.

Innym przykładem jest użycie pustej grupy po komendzie \LaTeX. Jest to zrobione po to, aby wymusić odstęp przed następnym słowem rozumie.

Układ

Przenoszenie wyrazów

Weźmy pod uwagę plik źródłowy przykład.tex:

\documentclass[a4paper,12pt]{article}
\usepackage[polish]{babel}
\usepackage[OT4]{fontenc}
\usepackage[utf8]{inputenc}
\pagestyle{empty}
\begin{document}
W tym akapicie występuje problem związany z przenoszeniem słowa dzwonnica.
To słowo trudno jest złamać tak, aby odstępy w linii nie były za duże lub za małe.
W związku z tym przy kompilacji generowane jest ostrzeżenie.
\end{document}

W wyniku kompilacji

$ latex przykład.tex

dostaniemy ostrzeżenie

Overfull \hbox (6.78139pt too wide) in paragraph at lines 7--12

W wyniku otrzymujemy taki akapit:

Aby temu zaradzić możemy na przykład zaproponować łamanie linii między słowami słowa i dzwonnica. Służy do tego komenda \linebreak. Modyfikujemy siódmą linię pliku źródłowego na

W tym akapicie występuje problem związany z przenoszeniem słowa\linebreak dzwonnica.

Kompilacja odbywa się już bez problemów, a wynikowy akapit wygląda teraz tak:

Teraz w pierwszej linii odstępy są trochę większe, co pogarsza wygląd estetyczny. Lepiej by było pewnie przeformułować jakoś to zdanie, żeby latex nie miał problemów z dzieleniem wyrazów.

Jeśli nie zależy nam aż tak bardzo na jakości, możemy pozwolić na użycie większych odstępów między wyrazami dodając w preambule polecenie \sloppy.

Czasami dzielenie wyrazów w niektórych słowach (np. w skrótach) nie jest pożądane.

Pisanie w \LaTeX-u znacznie się różni od tego co mamy w edytorach WYSIWYG.

W takim wypadku można zablokować łamanie wyrazu poprzez użycie polecenie \mbox{...}.

Pisanie w \LaTeX-u znacznie się różni od tego co mamy w edytorach \mbox{WYSIWYG}.

Łamanie linii i strony

Do łamania linii służy polecenie \\. Powoduje ono przejście do nowej linii. Do złamania strony służy polecenie \newpage. Żeby zacząć akapit bez wcięcia używamy \noindent.

W języku polskim nie zostawia się jednoliterowych spójników na końcu wiersza. Jednak latex może zdecydować, że linia zostanie złamana właśnie zaraz po spójniku. Aby temu zapobiec można użyć niełamliwych spacji, które wprowadza się za pomocą znaku tyldy ~.

\noindent Pierwsza linia.\\ Druga linia. Tutaj z kolei użyjemy niełamliwego odstępu, który często występuje w~języku polskim. Poniżej jeszcze raz to zdanie, ale bez niełamliwej spacji. Tutaj z kolei użyjemy niełamliwego odstępu, który często występuje w języku polskim.

Odstępy

Latex posiada sporo poleceń umożliwiających zmieniać domyślny układ graficzny. Tutaj pokażemy proste polecenia służące do wstawiania odstępu.

Do wstawienia odstępu poziomego służy polecenie \hspace{...}. Argumentem powinna być liczba zakończona przyrostkiem oznaczającym jednostki. Przykładowe jednostki to cm - centymetr, in - cal. Możemy też jako argument użyć polecenia \stretch{...}. Powoduje ono wstawienia takiego odstępu, aby aktualna linia została rozciągnięta na całą dostępną szerokość. Jeśli użyjemy więcej takich odstępów, to są one skalowane proporcjonalnie do wartości argumentów polecenia \stretch.

Analogiczne polecenie, które służy do wstawiania odstępów pionowych jest \vspace{...}.

\noindent Centymetr: $|$\hspace{1cm}$|$. Cal: $|$\hspace{1in}$|$.\\ 0\hspace{\stretch{1}}1\hspace{\stretch{3}}4\\ \vspace{3cm} Większe odstępy między liniami mogą być przydatne.

W przykładzie tym użyliśmy znaków $. Znak ten rozpoczyna i kończy tryb matematyczny, dzięki czemu możemy wstawiać różne ciekawe znaki. Zobacz także cześć poświęconą matematyce.

Znaki specjalne

Symbole specjalne

Niektóre znaki są interpretowane przez kompilator w specjalny sposób, więc nie można wstawić ich bezpośrednio, aby je uzyskać w tekście. Są to $ & % # _ { } ~ ^ \. Większość można otrzymać poprzedzając je znakiem \. Do trzech trzeba użyć trybu matematycznego. Polecenie \ (spacja poprzedzona \) oznacza pełnowymiarową spację.

\$ \& \% \# \_ \{ \} $\tilde{\ }$ $\hat{\ }$ $\backslash$

Cudzysłowy

W latexu cudzysłów " może mieć specjalne znaczenie (np. w trybie języka polskiego). Do tworzenia różnych cudzysłowów należy używać znaków , ' `. Jeżeli chcemy mieć podwójny cudzysłów, to wystarczy, że wprowadzimy dany znak dwa razy pod rząd.

Cudzysłowy angielskie: `x', ``tekst w cudzysłowach''. W języku polskim używamy ,,takich'' cudzysłowów.

Myślniki

Są trzy rodzaje myślników: -, --, ---. Pierwszy jest najkrótszy i jest stosowany jako łącznik lub do przenoszenia wyrazów. Drugi jest trochę dłuższy i używamy go np. do zakresów liczbowych. Trzeci jest najdłuższy i jest czasami stosowany jako zwykły myślnik.

Łącznik: np. 52-ego. Pauza: np. 12--17. Myślnik --- na przykład taki.

Złożone elementy

Bardziej złożone polecenia zapisywane są w postaci środowiska:

\begin{polecenie}
  Treść...
\end{polecenie}

Środowiska można zazwyczaj zagnieżdżać.

Listy

Do tworzenia list z punktami służą środowiska enumerate, itemize i description,.

\begin{enumerate} \item Pierwszy punkt listy wyliczeniowej: \begin{itemize} \item wypunktowanie, \item bez numerów. \end{itemize} \item W drugim punkcie jest podlista z opisami: \begin{description} \item[C/C++] język programowania; przez wielu programistów uważany za dosyć brzydki, \item[Java] tajne źródła podają, że to też jest język programowania. \end{description} \end{enumerate}

Tabele

Do tworzenia tabel służy środowisko tabular. To środowisko wymaga argumentu, który specyfikuje kolumny. Najprostsza specyfikacja składa się z ciągu liter określających sposób justowania ewentualnie przedzielonych znakiem | oznaczającym, że w tym miejscu ma być pionowa linia. Sposoby justowania to:

• l - równaj do lewej,
• c - centruj,
• r - równaj do prawej.

Wiersze w tabeli oddziela się poleceniem nowej linii \\, natomiast poszczególne kolumny oddzielamy znakiem &.

\begin{tabular}{r|cl} bardzo & prosta & tabela\\ \hline to & jest & drugi wiersz\\ & a to trzeci \end{tabular}

Wyrównanie

Do równania tekstu do lewej, bądź prawej służą środowiska flushleft i flushright. Do centrowania służy środowisko center.

\begin{flushleft} do\\ lewej \end{flushleft} \begin{center} do\\ środka \end{center} \begin{flushright} do\\ prawej \end{flushright}

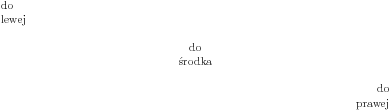
Przypisy

Przypisy wstawiamy poleceniem \footnote. Należy je wstawiać zaraz po wyrazie, po którym ma być przypis.

W tym akapicie\footnote{Innego akapitu tutaj nie ma.} jest przypis. Treść przypisu jest umieszczana na końcu strony.

Odsyłacze

W większych dokumentach, aby ułatwić czytelnikowi poruszanie się po nich, dobrze jest używać odsyłaczy. Kierują one czytelnika do innej części dokumentu, na przykład do danego paragrafu, tabeli, strony. Służą do tego polecenia \label{...}, \ref{...} i \pageref{...}.

Polecenie \label{etykieta} ustawia miejsce odniesienia o nazwie etykieta w danym miejscu kodu. Istotne jest, aby polecenie to wstawiać zaraz za miejscem, do którego chcemy się odsyłać.

Polecenie \ref{etykieta} odnosi się do miejsca wskazanego przez etykietę. W tekście polecenie to wstawia odpowiedni numer paragrafu, tabeli, itp., zależnie od tego jaki jest rodzaj wskazywanego elementu.

Polecenie \pageref{etykieta} również odnosi się do miejsca deklaracja etykiety, co w tekście jest widoczne jako numer strony, w której występuje miejsce odniesienia.

\section{Wstęp} \ldots \section{Użycie odsyłaczy}\label{odsylacze} W \LaTeX-u użycie odsyłaczy\ldots \section{Dzielenie dokumentu na części} \ldots Do odnoszenia się do innych części można używać odsyłaczy, patrz sekcja~\ref{odsylacze}.

Zauważmy, że podczas pierwszej kompilacji otrzymamy zapewne wśród komunikatów takie informacje:

No file odsyłacze.aux.
 
LaTeX Warning: Reference `odsylacze' on page 1 undefined on input line 13.
 
[1] (./odsyłacze.aux)
 
LaTeX Warning: There were undefined references.
 
 
LaTeX Warning: Label(s) may have changed. Rerun to get cross-references right.

Podczas pierwszej kompilacji tworzony jest plik odsyłacze.aux, który zawiera w sobie informacje o odsyłanych miejscach. Aby latex poprawnie wyliczył sobie i wstawił do tekstu odpowiednie odnośniki, niezbędna jest powtórna kompilacja.

Wstawki

Niektóre obiekty ( na przykład tabele czy rysunki) nie chcielibyśmy, aby były dzielone pomiędzy strony. Dodatkowo chcielibyśmy, aby można było dodawać im podpis, numerować je i mieć możliwość użycia odsyłaczy. Służą do tego środowiska table i figure. Środowiska te mają jeden opcjonalny argument. Zawartość takiego środowiska będzie wstawiona w tekście możliwie najbliżej miejsca, w którym zostało ono użyte. Zasady umiejscawiania wstawki są dosyć skomplikowane i efekty mogą być czasami irytujące. Warto więc zapoznać się w dokumentacji z zasadą działania wstawek.

Wewnątrz środowiska możemy użyć polecenia \caption{...}, które dodaje podpis.

Przykład mnożenia pisemnego liczb 23 i 37 można zobaczyć poniżej w tabeli \ref{mnozenie}. \begin{table}[!hbp] \centering \begin{tabular}{cl@{}l@{}l} & & 2 & 3\\ $\times$ & & 3 & 7\\ \hline $=$ & 1 & 6 & 1\\ $+$ & 6 & 9\\ \hline $=$ & 8 & 5 & 1 \end{tabular} \caption{Mnożenie pisemne}\label{mnozenie} \end{table} Tabela ta powinna być wstawiona gdzieś w tym akapicie. \LaTeX{} zrobi to automatycznie tak, aby było to możliwie blisko, zaraz po użyciu środowiska {\tt table}.

W tym przykładzie użyliśmy środowiska figure. Wewnątrz środowiska użyliśmy polecenia /centering, które powoduje, że obiekt będzie centrowany. Etykieta powinna znaleźć się zaraz po podpisie. Użyliśmy też argumentu opcjonalnego środowiska !hbp, który sugeruje latexowi, gdzie umieszczać wstawkę. ! mówi, aby pominąć niektóre parametry kontrolujące (dzięki temu bywa, że efekt jest bardziej zadowalający). h mówi, żeby spróbować umieścić wstawkę w miejscu jej pojawienia. Jeśli to się nie powiedzie to użycie b mówi, żeby spróbować umieścić wstawkę na dole strony. Jeśli wszystko zawiedzie, to p mówi, żeby wstawka znalazła się na stronie zawierającej tylko wstawki.

Zwróćmy też uwagę na użycie symbolu @ w specyfikacji kolumn tabeli. Otóż @{...} podaje tekst, który ma być użyty do rozdzielania kolumn. W tym przypadku tekst jest pusty, co daje efekt taki, że między kolumnami nie ma w ogóle odstępu.

Matematyka

Wprowadzanie wzorów matematycznych jest najsilniejszą stroną latexa. Możliwości są olbrzymie, dlatego przedstawimy kilka wybranych elementów, które pozwolą już wprowadzać większość formuł. Użytkownicy wprowadzający bardzo skomplikowane wzory chętnie skorzystają zapewne z dokumentacji oraz z dodatkowego pakietu ams-latex.

Tryb matematyczny

Aby pisać wzory, trzeba używać trybu matematycznego. Jeśli chcemy wstawić wzór wewnątrz akapitu, stosujemy składnie $...$. Można też eksponować wzór w osobnej linii. Przydatne jest to wtedy, gdy wzory są bardziej skomplikowane. Służy do tego składnia \[...\].

\noindent Suma $\sum_{k=1}^n k$, czyli suma liczb od 1 do $n$ wynosi $\frac{n(n+1)}{2}$: \[ \sum_{k=1}^n k = \frac{n(n+1)}{2}. \] Tą prostą równość można udowodnić na wiele sposobów.

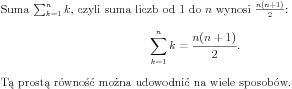
Widzimy, że formuły wewnątrz akapitu są trochę inaczej składane niż formuły eksponowane.

Tryb matematyczny znacznie różni się od trybu tekstowego. Na przykład odstępy są automatycznie wyliczane. Możemy zawsze użyć specjalnych komend powiększających odstępy takich jak \,, czy \quad.

Wzorom eksponowanym możemy nadawać etykiety, aby móc później się do nich odwoływać.

Grupowanie

Wiele konstrukcji wymaga (tak jak polecenia), aby ich elementy stanowiły zwartą całość. Dlatego często trzeba używać operatorów grupowania {...}, gdyż jeśli ich nie użyjemy, efekty mogą odbiegać od tego co chcemy uzyskać.

\[a^x+y \quad a^{x+y} \quad 2^16 \quad 2^{16}\]

Elementy

Pokażemy kilka przykładowych składników formuł.

Operatory _ i ^ służą do tworzenia indeksów dolnych i górnych.

\[ (x_1+x_2)^2 = x_1^2 + 2x_1x_2 + x_2^2 \]

Przy użyciu odpowiednich poleceń mamy dostępnych znacznie więcej symboli, jak na przykład litery greckie.

\[ \alpha + \beta + \gamma = 180^\circ \]

Podstawy takie jak pierwiastek \sqrt, ułamki \frac, nierówności \le.

\[ \sqrt{ab} \le \frac{a+b}{2} \]

Zmienne można dekorować dodając im różne znaczki lub je pogrubić.

\[ \dot{y} \quad \ddot{y} \quad f'(\hat{x}) \quad y
\quad \mathbf{x} \quad \vec{x} \quad \widehat{xyz} \]

Dostępnych jest wiele funkcji matematycznych (takich jak sin, lim) z użyciem poleceń. Funkcje mają być pisane czcionką prostą, stąd bierze się potrzeba użycia specjalnych poleceń.

\[ \lim_{h\to 0}\frac{\sin h}{h}=1 \]

Możemy mieć potrzebę stosowanie większych nawiasów we wzorach. Efekt ten można uzyskać, używając specjalnych poleceń, które określają rozmiar i stronę nawiasu. Za takim poleceniem powinien znaleźć się znak nawiasu, którego chcemy użyć.

Oczywiście mamy naprawdę sporo symboli matematycznych. Prawie wszystko, co powymyślali matematycy.

\[ A \subseteq B \Leftrightarrow \forall x\ x\in A\Rightarrow x\in B \]

Macierze

W trybie matematycznym środowiskiem pozwalającym tworzyć tablice i macierze jest array. Jest ono analogiczne do środowiska tabular z trybu tekstowego.

\[
  {\left( \begin{array}{cc}
    2 & 1\\
    1 & 3
  \end{array} \right)}^2
  =
  \left( \begin{array}{cc}
    5 & 5\\
    5 & 10
  \end{array} \right)
\]

Tutaj do powiększenia nawiasów użyliśmy poleceń \left i \right. Dobierają one rozmiar automatycznie.

Środowiska array można użyć też do wzoru z przypadkami.

\[
  |x| =
  \left\{ \begin{array}{ll}
    x & \textrm{ dla }x\ge 0,\\
    -x & \textrm{ dla }x < 0.
  \end{array} \right.
\]

Jako argument komendy \right daliśmy ., co oznacza, że w ogóle nie będzie prawego nawiasu. Ponadto zauważmy, że aby wstawić zwykły tekst wewnątrz formuły używa się polecenia \textrm{...}.

Równania wielolinijkowe

Normalnie nie można wprowadzać wzorów, które mają więcej niż jedną linię. W tym celu można użyć środowiska array, albo użyć trybu matematycznego eqnarray.

\begin{eqnarray}
  {(\sin x)}' & = & \cos x\\
  {(\cos x)}' & = & -\sin x\\
  {(x^n)}' & = & n x^{n-1}\nonumber
\end{eqnarray}

Widzimy, że równania w kolejnych linijkach są numerowane. Jeśli nie chcemy mieć numerów, możemy użyć wersji z *, tzn. \begin{eqnarray*}...\end{eqnarray*}, albo stosować polecenie \nonumber.

Co dalej?

Możliwości latexa są znacznie większe niż to co zostało tutaj przedstawione, a to za sprawą bogatej biblioteki pakietów, jakie zostały napisane. Przedstawimy po krótce najważniejsze z nich.

Tworzenie prezentacji - klasa beamer

Latex świetnie nadaje się do tworzenie prezentacji w postaci slajdów dzięki klasie dokumentów beamer. Posiada on dużo różnych możliwości.

• Klasa jest napisana z myślą o prostym i szybkim tworzeniu slajdów.
• Bardzo łatwo tworzy się nakładki, tzn. takie slajdy, w których elementy pojawiają się jeden po drugim.
• Posiada bogatą bibliotekę gotowych, praktycznych i dobrze dopracowanych wyglądów prezentacji, które można w bardzo prosty sposób zmieniać.
• No i oczywiście można korzystać z wszystkich atutów latexa.

Załączanie grafiki - pakiet graphicx

Podstawową sprawą jest możliwość dodawania grafiki. Służy do tego pakiet graphicx. Grafikę wstawia się za pomocą polecenia

\includegraphics{plik}

Polecenie to posiada szereg opcji. Są też ograniczenia co do formatu graficznego. Jeśli dokumentem docelowym ma być plik PS, to jedynym dozwolonym formatem jest EPS. Jeśli dokumentem docelowym ma być PDF, to dozwolone formaty to PDF, PNG, JPEG i GIF.

Wbudowana grafika - pakiet pgf

Grafikę można też tworzyć bezpośrednio w latexu za pomocą gotowych pakietów. Wadą takiego podejścia jest jednak brak wizualnego tworzenia. Zaletą jest jednak to, że możemy z łatwość łączyć rysunki z latexem. Na przykład z łatwością możemy umieszczać na rysunku skomplikowane formuły matematyczne.

Spośród kilku pakietów przeznaczonych do tego celu jednym z najbardziej dopracowanych jest pakiet pgf (skrót od Portable Graphics Format). Ponadto jedną z jego podstawowych zalet jest, że dokumenty napisane z jego użyciem, można eksportować zarówno do plików PS jak i PDF.