Informatyka MIMUW

W rozdziale tym zdefiniujemy automat - drugi, obok gramatyki, model obliczeń. Określimy język rozpoznawany przez automat i podamy warunki równoważne na to, by język był rozpoznawany.

Automaty

Wprowadzimy teraz pojęcie automatu. Jak już wspomnieliśmy w wykładzie drugim automat to drugi, obok gramatyki, model obliczeń będący przedmiotem badań teorii języków i automatów. Model realizujący warunek efektywności analitycznej, czyli taki na podstawie którego możliwe jest sformułowanie algorytmu rozstrzygającego w skończonej liczbie kroków, czy dowolne słowo należy, czy też nie należy do języka rozpoznawanego przez ten automat. Lub inaczej możemy powiedzieć, że taki automat daje algorytm efektywnie rozstrzygający, czy dowolne obliczenie sformułowane nad alfabetem automatu jest poprawne.

Wprowadzony w tym wykładzie automat, zwany automatem skończenie stanowym, jest jednym z najprostszych modeli obliczeń. Jest to model z bardzo istotnie ograniczoną pamięcią. Działanie takiego automatu sprowadza się do zmiany stanu pod wpływem określonego zewnętrznego sygnału czy impulsu.

Pomimo tych ograniczeń urządzenia techniczne oparte o modele takich automatów spotkać możemy dość często. Jako przykład służyć mogą automatyczne drzwi, automaty sprzedające napoje, winda, czy też urządzenia sterujące taśmą produkcyjną.

Przykład 1.1.

Drzwi automatycznie otwierane są sterowane automatem, którego działanie opisać można, przyjmując następujące oznaczenia. Fakt, że osoba chce wejść do pomieszczenia zamykanego przez takie drzwi, identyfikowany przez odpowiedni czujnik, opiszemy symbolem \(\displaystyle WE\). Zamiar wyjścia symbolem \(\displaystyle WY\). Symbol \(\displaystyle WEWY\) będzie związany z równoczesnym zamiarem wejścia jakiejś osoby i wyjścia innej. Wreszcie symbol \(\displaystyle BRAK\) oznaczał będzie brak osób, które chcą wejść lub wyjść. Zatem zbiór \(\displaystyle \{ WE, WY,WEWY,BRAK \}\), to alfabet nad którym określimy automat o \(\displaystyle 2\) stanach: \(\displaystyle OTWARTE, ZAMKNIĘTE\) poniższym grafem.

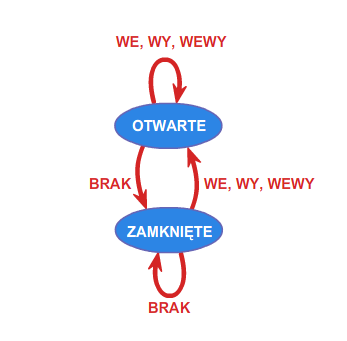
Automaty reagują więc na określone sygnały zewnętrzne reprezentowane przez litery alfabetu \(\displaystyle A\), zmieniając swój stan. Jeśli ustalimy stan początkowy automatu oraz dopuszczalne stany końcowe, to automat będzie testował dowolne słowo z \(\displaystyle A^{*}\) , startując ze stanu początkowego. Jeśli rezultatem finalnym działania automatu (obliczenia) będzie stan końcowy, to słowo będzie rozpoznawane przez automat, a obliczenie określone takim słowem poprawne. Automaty można graficznie reprezentować jako etykietowane grafy skierowane. W takim grafie każdy wierzchołek odpowiada stanowi automatu, a każda strzałka pomiędzy wierzchołkami \(\displaystyle u\) i \(\displaystyle v\), etykietowana symbolem \(\displaystyle a\), oznacza rzejście automatu ze stanu \(\displaystyle u\) do stanu \(\displaystyle v\) pod wpływem litery \(\displaystyle a\). Podamy teraz definicję automatu. Niech \(\displaystyle A\) oznacza dowolny alfabet. Od tego momentu wykładu zakładamy, że alfabet jest zbiorem skończonym.

Definicja 1.1

Automatem nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A} \displaystyle =(S,f)\), w którym

\(\displaystyle S\) - jest dowolnym skończonym zbiorem zwanym zbiorem stanów,

\(\displaystyle f: S \times A \rightarrow S\) - jest funkcją przejść.

Automat będąc w stanie \(\displaystyle s_{i}\) po przeczytaniu litery \(\displaystyle a\) zmienia stan na \(\displaystyle s_{j}\) zgodnie z funkcją przejścia \(\displaystyle f(s_{i},a)=s_{j}\) .

Funkcję przejść rozszerzamy na cały wolny monoid \(\displaystyle A^{*}\) do postaci

przyjmując:

dla każdego \(\displaystyle s \in S\;\;\;f(s,1) = s\) oraz

dla każdego \(\displaystyle s \in S,\;\;a \in A\) i dla dowolnego \(\displaystyle w \in A^*\)

Działanie automatu pokazane jest na poniższej animacji 2.

Zdefiniowany powyżej automat \(\displaystyle \mathcal{A}\) nazywamy skończonym lub skończenie stanowym ze względu na założenie skończoności zbioru stanów \(\displaystyle S\).

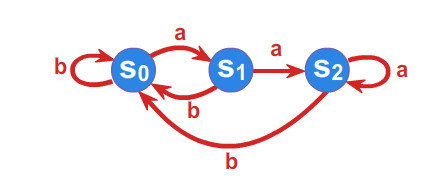
Przykład 1.2.

Niech \(\displaystyle A=\left\{ a,b\right\}\) będzie alfabetem, a \(\displaystyle \mathcal{A}=(S,f)\) automatem takim, że

\(\displaystyle S=\left\{ s_{0},s_{1},s_{2}\right\}\) , a funkcja przejść zadana jest przy pomocy tabelki

Automat możemy również jednoznacznie określić przy pomocy grafu.

Podamy teraz bardzo interesujący przykład zastosowania automatów skończonych. Przedstawimy mianowicie wykorzystanie tak zwanych automatów synchronizujących w przemyśle. Automat synchronizujący nad alfabetem \(\displaystyle A\) to automat \(\displaystyle (S,f)\) o następującej własności: istnieje stan \(\displaystyle t \in S\) oraz słowo \(\displaystyle w \in A^*\) takie, że dla każdego stanu \(\displaystyle s\) tego automatu \(\displaystyle f(s, w)=t\). Istnieje więc pewne uniwersalne słowo \(\displaystyle w\), pod wpływem którego wszystkie stany przechodzą w jeden, ustalony stan automatu \(\displaystyle t \in S\). Mówimy, że następuje wtedy synchronizacja wszystkich stanów automatu.

Poniżej prezentujemy przykład zaczerpnięty z pracy Ananicheva i Volkova (D. S. Ananichev, M. V. Volkov, Synchronizing Monotonic Automata, Lecture Notes in Computer Science, 2710(2003), 111-121.), ukazujący ideę użycia automatów synchronizujących w tej dziedzinie.

Przykład 1.3.

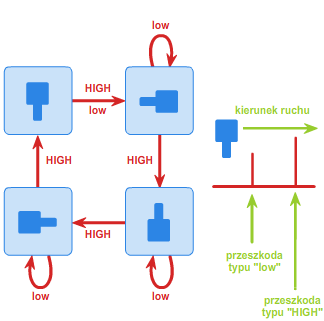
Załóżmy, że pewna fabryka produkuje detale w kształcie kwadratu z "wypustką" na jednym boku (patrz rys. 3). Po wyprodukowaniu detale należy umieścić w opakowaniach w ten sposób, by wszystkie były w tej samej orientacji - mianowicie "wypustką" w lewo.

Załóżmy ponadto dla uproszczenia, że detale mogą przyjmować jedną z czterech orientacji (rys. 4): "wypustką" w górę, w dół, w lewo lub w prawo.

Należy zatem skonstruować takie urządzenie (orienter), które będzie ustawiało wszystkie detale w żądanej orientacji. Oczywiście istnieje wiele metod rozwiązania tego problemu, ale z praktycznego punktu widzenia potrzebne jest rozwiązanie najprostsze i najtańsze. Jednym z takich sposobów jest umieszczanie detali na pasie transmisyjnym z zamontowaną wzdłuż niego pewną ilością przeszkód dwojakiego rodzaju: niskich (low) oraz wysokich (HIGH). Wysoka przeszkoda ma tę własność, że każdy detal, który ją napotka, zostanie obrócony o 90 stopni w prawo (zakładamy, że elementy jadą od lewej do prawej strony). Przeszkoda niska obróci o 90 stopni w prawo tylko te detale, które są ułożone "wypustką" w dół. Na rys. 5 przedstawione zostały przejścia pomiędzy orientacjami detali w zależności od napotkania odpowiedniej przeszkody.

Można zauważyć, że automat z rysunku 5 jest automatem synchronizującym. Słowem, które go synchronizuje, jest następująca sekwencja przeszkód:

low-HIGH-HIGH-HIGH-low-HIGH-HIGH-HIGH-low.

Niezależnie od tego, w jakiej orientacji początkowej znajduje się detal, po przejściu przez powyższą sekwencję przeszkód zawsze będzie ułożony "wypustką" w lewo. Sytuację przedstawia poniższa animacja 3:

Rozszerzymy teraz wprowadzone pojęcie automatu w ten sposób, by uzyskać możliwość efektywnego rozstrzygania, czy dowolne słowo utworzone nad alfabetem \(\displaystyle A\) reprezentuje poprawne obliczenie, czyli spełnia kryteria określone przez rozszerzony automat.

Definicja 1.2.

Język \(\displaystyle \; L~\subset A^* \;\) jest rozpoznawany (akceptowany) wtedy i tylko wtedy, gdy istnieje automat skończony \(\displaystyle \mathcal{A} \displaystyle = (S,f) , \;\) stan \(\displaystyle \; s_0 \in S \;\) oraz zbiór \(\displaystyle \; T \subset S \;\) takie, że

Stan \(\displaystyle s_0 \;\) nazywamy stanem początkowym, a \(\displaystyle \; T \;\) zbiorem stanów końcowych automatu \(\displaystyle \mathcal{A}\) .

Rozszerzony w powyższy sposób automat, poprzez dodanie stanu początkowgo i zbioru stanów końcowych, w dalszym ciągu nazywamy automatem i oznaczamy jako piątkę \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) lub czwórkę \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\), jeśli wiadomo, nad jakim alfabetem rozważamy działanie automatu.

Fakt, że język \(\displaystyle \; L \;\) jest rozpoznawany przez automat \(\displaystyle \mathcal{A},\) zapisujemy jako

Rodzinę wszystkich języków rozpoznawalnych nad alfabetem \(\displaystyle A\) oznaczamy przez \(\displaystyle \mathcal{REC}(\mathcal{A}^{*})\) .

Podobnie jak w przypadku gramatyk nie ma jednoznacznej odpowiedniości pomiędzy językami rozpoznawalnymi a automatami. Wprowadza się więc relację, która identyfikuje automaty rozpoznające ten sam język.

Definicja 1.3.

Automaty \(\displaystyle \mathcal{A}_{1}\) i \(\displaystyle \mathcal{A}_{2}\) są równoważne, jeśli rozpoznają ten sam język, czyli

W dalszych rozważaniach języków rozpoznawanych ograniczymy się do automatów \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\), które spełniają warunek \(\displaystyle f(s_0,A^*) = S.\) Nie zawęża to naszych rozważań. Jeśli bowiem język \(\displaystyle \; L \;\) jest rozpoznawany przez pewien automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\), to jest również rozpoznawany przez automat

który spełnia powyższy warunek. Zauważmy, że przyjmując to założenie, upraszczamy strukturę automatu. Z punktu widzenia grafu automatu można powiedzieć, że nie występują w nim wierzchołki (stany) nieosiagalne z \(\displaystyle s_0\). Poniżej przedstawiamy algorytm usuwający z automatu stany nieosiągalne ze stanu początkowego.

Algorytm UsuńStanyNieosiągalne - usuwa z automatu \(\displaystyle \mathcal{A}\) stany nieosiągalne

for each p in S do
    zaznaczone[p] <- 0;
end for
zaznaczone[s_0] <- 1;
OZNACZ (s_0);
S' <- {s in S: zaznaczone[s]=1};
T' <- T cap S';
flag <-false  # jeśli nie dodamy stanu to na końcu pętli nadal flag=false
f' <- f;
for each  p in S do
  for each  a in A do
    if  f'(p,a)=NULL then
      f'(p,a)<- s_f; # f'(p,a) była nieokreślona
      flag  <-true; 
    end if
  end for
end for
if flag=true then
   S'<- S' cup {s_f};
end if 
return  A'=(S', A, f', s_0, T');

Algorytm Procedure Oznacz

procedure OZNACZ (x in S)
for each  p in S 
  flag <-false
  for each  a in A do
    if  f(x,a)=p then
      flag <-true
    end if
  end for
  if flag=true and zaznaczone [p]=0 then
    zaznaczone [p] <- 1;
    OZNACZ (p);
  end if
end for
end procedure

Powyższy algorytm, dla ustalonego alfabetu \(\displaystyle A\), posiada złożoność \(\displaystyle O(|A| \cdot |S|)\), czyli liniową względem liczby stanów.

Przedstawiając automat przy pomocy grafu przyjmujemy następującą konwencję. Jeśli w automacie występuje stan początkowy, oznaczać go będziemy zieloną strzałką wchodzącą do tego stanu. Jeśli w automacie występują stany końcowe, oznaczać je będziemy niebieską obwódką.

Przykład 1.4.

Jeśli w przykładzie 1.2 (patrz przykład 1.2.) przyjmiemy stan \(\displaystyle s_{0}\) jako stan początkowy, \(\displaystyle T=\left\{ s_{2}\right\}\) jako zbiór stanów końcowych, to automat \(\displaystyle \mathcal{A} = (S,A,f,s_0,T)\) rozpoznaje język

złożony ze słów, kończących się na \(\displaystyle a^2\) .

Słowo \(\displaystyle aba\) nie jest akceptowane.

Słowo \(\displaystyle abaa\) jest akceptowane.

Każdy automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) wyznacza w wolnym monoidzie \(\displaystyle A^*\) prawą kongruencję, nazywaną prawą kongruencją automatową, określoną w następujący sposób:
\(\displaystyle \forall u,v \in A^*\)

Dla automatu skończonego (o skończonym zbiorze stanów), a takie rozważamy, relacja \(\displaystyle \sim _{A}\) ma skończony indeks, czyli skończoną liczbę klas równoważności.

Przykład 1.5.

Automat z przykładu 1.2 (patrz przykład 1.2.) ze stanem \(\displaystyle s_{0}\) jako początkowym wyznacza relację równoważności o trzech klasach:

\(\displaystyle [1]=A^*\left\{ b \right\}\cup \left\{ 1\right\}\),
\(\displaystyle [a]=A^*\left\{ ba\right\} \cup \left\{ a\right\}\),
\(\displaystyle [a^2]=A^*\left\{ a^2 \right\}.\)

Na odwrót, każda prawa kongruencja \(\displaystyle \rho \subset (A^*)^2\) wyznacza automat, zwany ilorazowym, w następujący sposób:

\(\displaystyle \mathcal{A} \displaystyle _\rho\) jest automatem ze stanem początkowym \(\displaystyle [1]_\rho\). \(\displaystyle \mathcal{A}_{\rho }\) jest automatem skończonym wtedy i tylko wtedy, gdy relacja \(\displaystyle \rho\) ma skończony indeks.
Z definicji prawej kongruencji wynika, że funkcja przejść \(\displaystyle f^*\) jest określona poprawnie.

Definicja 1.4.

Niech \(\displaystyle \mathcal{A} \displaystyle =(S,f)\) i \(\displaystyle \, \mathcal{B} \displaystyle =(T,g)\) będą dowolnymi automatami. Odwzorowanie \(\displaystyle \varphi:S\longrightarrow T\) nazywamy homomorfizmem automatów wtedy i tylko

wtedy, jeśli

Homomorfizm automatów oznaczamy \(\displaystyle \varphi :\mathcal{A}\longrightarrow \mathcal{B}\) .

Twierdzenie 1.1.

Prawdziwe są następujące fakty:

(1) Dla dowolnej prawej kongruencji \(\displaystyle \; \rho \; \subset \; (A^*)^2\)

(2) Dowolny automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) jest izomorficzny z automatem \(\displaystyle \mathcal{A}_{\sim _{\mathcal{A}}}\) ,

(3) Dla dowolnych automatów \(\displaystyle \mathcal{A}_1 \displaystyle = (S_1,A,f_1,s^1_0,T_1)\) i \(\displaystyle \mathcal{A}_2 \displaystyle = (S_2,A,f_2,s^2_0,T_2)\) prawdziwa jest równoważność

\(\displaystyle \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2}\: \: \Longleftrightarrow \:\) istnieje epimorfizm \(\displaystyle \varphi :\mathcal{A}_1\longrightarrow \mathcal{A}_2\) taki, że \(\displaystyle \varphi(s^1_0) = s^2_0\).

Dowód

(1) Identyczność relacji wynika wprost z definicji automatu ilorazowego \(\displaystyle \mathcal{A} \displaystyle _\rho\) oraz prawej kongruencji \(\displaystyle \sim _{A_{\rho }}\) .

(2) Rozważmy automat \(\displaystyle \mathcal{A} \displaystyle = (S,A,f,s_0,T)\) i odwzorowanie

gdzie \(\displaystyle \forall s\in S\)

Istnienie słowa \(\displaystyle w\) wynika z faktu, że \(\displaystyle s_0\) jest stanem początkowym, natomiast z definicji relacji \(\displaystyle \sim _{\mathcal{A}}\) wynika, że odwzorowanie \(\displaystyle \psi\) jest poprawnie określone.
Odwzorowanie \(\displaystyle \psi\) ma być homomorfizmem, czyli dla każdego stanu \(\displaystyle s\in S\) i dowolnego słowa \(\displaystyle w\in A^{*}\) spełniać warunek

Warunek ten wynika z następujących równości

gdzie \(\displaystyle f(s_0,u)=s\).

Z prostych obserwacji wynika, że \(\displaystyle \psi\) jest suriekcją i iniekcją.

(3) Dowód implikacji "\(\displaystyle \Rightarrow\)"
Załóżmy, że \(\displaystyle \: \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2 }\) . Niech

będzie odwzorowaniem takim, że

\(\displaystyle \forall s\in S_1\) \(\displaystyle \varphi (s) = f_2(s^2_0,w),\;\;\text{gdzie}\;\; w\in A^{*}\;\; i \;\; f_1(s^1_0,w) = s.\)

Stąd, że \(\displaystyle s^1_0\) jest stanem początkowym automatu \(\displaystyle \mathcal{A}_1,\) wynika, że istnieje słowo \(\displaystyle \; w \in A^* \;\) potrzebne do określenia epimorfizmu \(\displaystyle \varphi\).
Z założenia \(\displaystyle \: \sim _{\mathcal{A}_1}\: \subseteq \: \sim _{\mathcal{A}_2}\) wynika, że \(\displaystyle \varphi \;\) jest poprawnie zdefiniowaną funkcją.
Uzasadnienie faktu, że \(\displaystyle \varphi\) jest homomorfizmem, jest analogiczne jak w punkcie (2) dla \(\displaystyle \psi\).
\(\displaystyle \varphi\) jest suriekcją, gdyż \(\displaystyle \; s^2_0 \;\) jest stanem początkowym automatu \(\displaystyle \mathcal{A}_2\) .
\(\displaystyle \; \varphi (s^1_0) = s^2_0, \;\) ponieważ \(\displaystyle \; f_1(s^1_0,1) = s^1_0\).
Dowód implikacji "\(\displaystyle \Leftarrow\)"
Niech \(\displaystyle \varphi :\mathcal{A}_1\longrightarrow \mathcal{A}_2\) będzie epimorfizmem takim, że \(\displaystyle \; \varphi (s^1_0) = s^2_0 \;\).
Wówczas prawdziwy jest następujący ciąg wnioskowań.

To oznacza, że \(\displaystyle \sim _{\mathcal{A}_1}\subseteq \sim _{\mathcal{A}_2}\) .

Symbolem \(\displaystyle S^S\) oznaczamy rodzinę wszystkich funkcji określonych na zbiorze \(\displaystyle S\) i przyjmujących wartości w \(\displaystyle S\). Łatwo zauważyć, iż rodzina ta wraz ze składaniem odwzorowań jest monoidem \(\displaystyle (S^S,\circ)\) .

Definicja 1.5.

Reprezentacja automatu jest homomorfizmem monoidu \(\displaystyle A^*\) w monoid \(\displaystyle S^S\), bowiem dla dowolnych \(\displaystyle v,w \in A^*\) spełnione są warunki

Definicja 1.6.

Niech \(\displaystyle \mathcal{A} \displaystyle = (S,f)\) będzie dowolnym automatem. Monoidem przejść automatu \(\displaystyle \mathcal{A}\) nazywamy monoid

Następujące wnioski są konsekwencjami rozważań przeprowadzonych powyżej.

Wniosek 1.1.

(1) Monoid przejść automatu \(\displaystyle \mathcal{A}\) jest podmonoidem monoidu \(\displaystyle S^S\) i zbiór \(\displaystyle \left\{ \tau _{\mathcal{A}}(a):a\in A\right\}\) jest zbiorem generatorów tego monoidu.

Wynika to z faktu, że \(\displaystyle \tau _{\mathcal{A}}\) jest epimorfizmem i z twierdzenia 2.1 z wykładu 1. (patrz twierdzenie 2.1. wykład 1)

(2) Monoid przejść automatu skończonego jest skończony.

(3) Monoid przejść automatu \(\displaystyle \mathcal{A}\) jest izomorficzny z monoidem ilorazowym \(\displaystyle A^{*}/_{Ker_{\tau _{\mathcal{A}}}}\) .

Jest to wniosek z twierdzenia o rozkładzie epimorfizmu, które w tym przypadku ilustruje poniższy diagram.

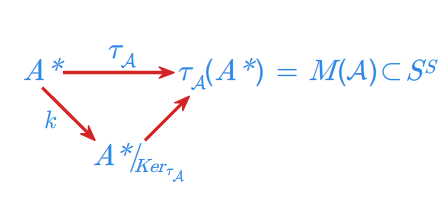
Przykład 1.6.

Określimy monoid przejść dla automatu z przykładu 1.2 (patrz przykład 1.2.). Wypisujemy kolejne funkcje \(\displaystyle \tau _{\mathcal{A}}(w)\) dla \(\displaystyle w\in \{a,b\}^{*}\) . Zauważmy, że ze względu na występujące w tabelce powtórzenia, będące wynikiem równości, np. \(\displaystyle \tau _{\mathcal{A}}(b^2)=\tau _{\mathcal{A}}(b),\) nie ma potrzeby określać funkcji \(\displaystyle \tau _{\mathcal{A}}(b^{n})\) dla \(\displaystyle n\geq 3\) . Podobna obserwacja ma miejsce w innych przypadkach, co sprawia, że tabelka zawiera skończoną liczbę różnych funkcji.

Poniżej zamieszczamy algorytm obliczający monoid przejść dla automatu skończenie stanowego.

Algorytm WyznaczMonoidPrzejść - wyznacza monoid przejść dla automatu

Wejście: A=(S, A, f, s_0, T) - automat
Wyjście:  M - monoid przejść dla  \mathcal{A}
L <- emptyset;   #L jest listą
M <- emptyset;
for each a in A cup {1} do
  insert (L, {tau_A(a)}); # gdzie  tau_A(a)(s)=f(s, a) dla każdego s in S
end for
while  L not = emptyset; do 
  tau_A(w) <- first(L);
  M <- M cup tau_A(w);
  for each  a in A do
    for each  s in S do
      tau'_A(wa)(s)<- f(tau_A(w)(s),a);
    end for
    if  tau'_A(wa) not in L cup M 
      insert (L, tau'_A(wa));
    end if
  end for
end while
return  M;

Procedura insert\(\displaystyle (L, x)\) wkłada na koniec listy \(\displaystyle L\) element \(\displaystyle x\). Funkcja first\(\displaystyle (L)\) wyjmuje pierwszy element znajdujący się na liście \(\displaystyle L\) i zwraca go. Algorytm działa w następujący sposób: najpierw na listę \(\displaystyle L\) wkładane są elementy monoidu przejść \(\displaystyle \tau_{\mathcal{A}}(a)\) dla każdej litery \(\displaystyle a \in A \cup 1\). Te funkcje można obliczyć bezpośrednio z tabelki reprezentującej funkcję przejścia automatu \(\displaystyle \mathcal{A}\). Następnie z listy po kolei ściągane są poszczególne funkcje \(\displaystyle \tau_{\mathcal{A}}(w)\). Każda z nich dodawana jest do zbioru \(\displaystyle M\), a następnie algorytm sprawdza dla każdej litery \(\displaystyle a \in A\), czy funkcja \(\displaystyle \tau_{\mathcal{A}}(wa)\) istnieje już na liście \(\displaystyle L\) lub w zbiorze \(\displaystyle M\). Jeśli nie, to funkcja ta dodawana jest do listy. Procedura powyższa trwa do czasu, gdy lista \(\displaystyle L\) zostanie pusta. Wtedy wszystkie elementy monoidu przejść znajdą się w zbiorze \(\displaystyle M\).

Przeanalizujmy działanie algorytmu dla automatu z przykładu 1.2 (patrz przykład 1.2.).

Na początku na listę \(\displaystyle L\) włożone zostaną funkcje \(\displaystyle \tau_{\mathcal{A}}(1)\), \(\displaystyle \tau_{\mathcal{A}}(a)\) oraz \(\displaystyle \tau_{\mathcal{A}}(b)\). Z listy zdejmujemy funkcję \(\displaystyle \tau_{\mathcal{A}}(1)\) i dodajemy ją do zbioru \(\displaystyle M\). Ponieważ \(\displaystyle \forall a \in A\displaystyle \tau_{\mathcal{A}}(1a)=\tau_{\mathcal{A}}(a)\), a funkcje \(\displaystyle \tau_{\mathcal{A}}(a)\) oraz \(\displaystyle \tau_{\mathcal{A}}(b)\) znajdują się już na liście, zatem nie dodajemy ich do \(\displaystyle L\). Bierzemy kolejny element listy, \(\displaystyle \tau_{\mathcal{A}}(a)\), dodajemy go do \(\displaystyle M\) i obliczamy funkcje \(\displaystyle \tau_{\mathcal{A}}(aa)\) oraz \(\displaystyle \tau_{\mathcal{A}}(ab)\). Ponieważ \(\displaystyle \tau_{\mathcal{A}}(aa)\) nie jest tożsama z żadną funkcją ze zbioru \(\displaystyle L \cup M\), dodajemy ją do listy. Funkcja \(\displaystyle \tau_{\mathcal{A}}(ab)\) również nie jest równa żadnej z funkcji należących do zbioru \(\displaystyle L \cup M\), zatem wstawiamy ją na koniec listy. Na liście \(\displaystyle L\) mamy zatem teraz następujące elementy: \(\displaystyle \tau_{\mathcal{A}}(b)\), \(\displaystyle \tau_{\mathcal{A}}(a^2)\) oraz \(\displaystyle \tau_{\mathcal{A}}(ab)\). Zdejmujemy z listy funkcję \(\displaystyle \tau_{\mathcal{A}}(b)\), dodajemy ją do \(\displaystyle M\) i obliczamy \(\displaystyle \tau_{\mathcal{A}}(ba)\) oraz \(\displaystyle \tau_{\mathcal{A}}(bb)\). Pierwsza z tych funkcji jest nowa, tzn. nie jest tożsama z żadną funkcją ze zbioru \(\displaystyle L \cup M\) więc dodajemy ją na koniec listy. Druga z nich równa jest funkcji \(\displaystyle \tau_{\mathcal{A}}(b)\), więc nie dodajemy jej do listy. W tym momencie zbiór \(\displaystyle M\) zawiera następujące elementy: \(\displaystyle \tau_{\mathcal{A}}(1)\), \(\displaystyle \tau_{\mathcal{A}}(a)\), \(\displaystyle \tau_{\mathcal{A}}(b)\), natomiast lista zawiera elementy \(\displaystyle \tau_{\mathcal{A}}(a^2)\), \(\displaystyle \tau_{\mathcal{A}}(ab)\), \(\displaystyle \tau_{\mathcal{A}}(ba)\). Zdejmujemy z \(\displaystyle L\) funkcję \(\displaystyle \tau_{\mathcal{A}}(a^2)\), dodajemy ja do \(\displaystyle M\) i ponieważ \(\displaystyle \tau_{\mathcal{A}}(a^2a)=\tau_{\mathcal{A}}(a^2)\) i \(\displaystyle \tau_{\mathcal{A}}(a^2b)=\tau_{\mathcal{A}}(b)\), nic nie dodajemy do \(\displaystyle L\). Zdejmujemy teraz z listy funkcję \(\displaystyle \tau_{\mathcal{A}}(ab)\), dodajemy ją do \(\displaystyle M\) i ponieważ \(\displaystyle \tau_{\mathcal{A}}(aba)\) nie należy do \(\displaystyle L \cup M\) dodajemy ją do listy. \(\displaystyle \tau_{\mathcal{A}}(abb)=\tau_{\mathcal{A}}(b)\), więc tej funkcji nie dodajemy do \(\displaystyle L\). Z \(\displaystyle L\) ściągamy \(\displaystyle \tau_{\mathcal{A}}(ba)\), dodajemy ją do \(\displaystyle M\) i widzimy, że \(\displaystyle \tau_{\mathcal{A}}(baa)=\tau_{\mathcal{A}}(a^2)\) oraz \(\displaystyle \tau_{\mathcal{A}}(bab)=\tau_{\mathcal{A}}(b)\), więc nic nie dodajemy do \(\displaystyle L\). Na liście pozostała funkcja \(\displaystyle \tau_{\mathcal{A}}(aba)\). Ściągamy ją z listy i dodajemy do \(\displaystyle M\). Widzimy, że \(\displaystyle \tau_{\mathcal{A}}(abaa)=\tau_{\mathcal{A}}(a^2)\) i \(\displaystyle \tau_{\mathcal{A}}(abab)=\tau_{\mathcal{A}}(b)\), zatem nic nie dodajemy do listy \(\displaystyle L\). Lista jest w tym momencie pusta i działanie algorytmu zakończyło się. Ostatecznie mamy

co zgadza się z wynikiem otrzymanym w przykładzie.

Twierdzenie poniższe zbiera dotychczas uzyskane charakteryzacje języków rozpoznawanych.

Twierdzenie 1.2.

Niech \(\displaystyle \; L \subset A^* \;\) będzie dowolnym językiem. Równoważne są następujące warunki:

(1) Język \(\displaystyle \; L \;\) jest rozpoznawalny,

(2) Język \(\displaystyle \; L \;\) jest sumą wybranych klas równoważności pewnej prawej kongruencji \(\displaystyle \rho\) na \(\displaystyle \; A^* \;\) o skończonym indeksie:

\(\displaystyle L = \bigcup_{w\in L}[w]_\rho.\)

(3) Język \(\displaystyle \; L \;\) jest sumą wybranych klas równoważności pewnej kongruencji \(\displaystyle \rho\) na \(\displaystyle \; A^* \;\) o skończonym indeksie:

\(\displaystyle L = \bigcup_{w\in L}[w]_\rho.\)

(4) Istnieje skończony monoid \(\displaystyle \; M \;\) i istnieje epimorfizm \(\displaystyle \varphi : A^* \longrightarrow M\) taki, że

\(\displaystyle L = \varphi^{-1}(\varphi (L)).\)

Dowód

Dowód równoważności czterech powyższych warunków przeprowadzimy zgodnie z następującym schematem:

\(\displaystyle 4 \Longrightarrow 3\)

Dany jest homomorfizm

gdzie \(\displaystyle M\) jest skończonym monoidem.
Określamy relację \(\displaystyle \; \rho \;\) na \(\displaystyle A^*\), przyjmując dla dowolnych \(\displaystyle u, v \in A^*\)

Tak określona relacja jest kongruencją. Natomiast jej skończony indeks wynika z faktu, że monoid \(\displaystyle \; M \;\) jest skończony. Pokażemy teraz, że:

Inkluzja \(\displaystyle \; \subseteq \;\) jest oczywista.
Inkluzja w przeciwną stronę (\(\displaystyle L \supseteq \bigcup_{w\in L}[w]_\rho,\)) oznacza, że każda klasa równoważności relacji \(\displaystyle \; \rho \;\) albo cała zawiera się w języku \(\displaystyle L\), albo cała zawiera się w uzupełnieniu języka \(\displaystyle L\).
Załóżmy, że \(\displaystyle \; u \in [w]_\rho\) dla pewnego \(\displaystyle w \in L. \;\) Oznacza to, że

Implikuje to ostatecznie, że \(\displaystyle u \in L\).

\(\displaystyle 3 \Longrightarrow 2\)

Każda kongruencja jest prawą kongruencją.

\(\displaystyle 2 \Longrightarrow 1\)

Niech \(\displaystyle \; \rho \;\) będzie prawą kongruencją o skończonym indeksie na \(\displaystyle \; A^* \;\) taką, że

Automat \(\displaystyle \mathcal{A}_{\rho } \displaystyle = (A^*/\rho,f^*,[1]_\rho,T),\) dla którego

akceptuje język \(\displaystyle L\).

\(\displaystyle 1 \Longrightarrow 4\)

Niech język \(\displaystyle \; L=L(\mathcal{A}) \;\), gdzie \(\displaystyle \mathcal{A} \displaystyle = (S,f,s_0,T)\).
Określamy odwzorowanie

przyjmując dla każdego \(\displaystyle v\in A^{*}\)

Jest to odwzorowanie kanoniczne monoidu \(\displaystyle \; A^* \;\) na monoid ilorazowy, a więc jest to epimorfizm.
\(\displaystyle A^{*}/_{Ker\tau _{\mathcal{A}}}\) jest monoidem skończonym, ponieważ \(\displaystyle \; S \;\) jest zbiorem skończonym.

Dla dowodu równości \(\displaystyle L = \varphi^{-1}(\varphi (L))\) wystarczy udowodnić inkluzję \(\displaystyle L \supset \varphi^{-1}(\varphi (L))\). (Inkluzja \(\displaystyle \; L \subseteq \varphi^{-1}(\varphi (L))\;\) wynika z definicji przeciwobrazu.)
Niech \(\displaystyle \; u \in \varphi^{-1}(\varphi (L)) .\;\) Oznacz to, że

W szczególności

czyli \(\displaystyle u \in L. \)