Informatyka MIMUW

W tym wykładzie określimy rodzinę języków regularnych wolnego monoidu \(A^{*}\) oraz pewien formalny opis tych języków zwany wyrażeniami regularnymi.
Dla języka rozpoznawalnego \(L\) wprowadzimy pojęcie automatu minimalnego rozpoznającego \(L\) i prawej kongruencji syntaktycznej, która odgrywa istotną rolę w problemach związanych z automatem minimalnym.

Wyrażenia regularne

Definicja 1.1

Niech \(A\) będzie skończonym alfabetem. Rodzina \(\mathcal{REG}(A^{*})\) języków regularnych nad alfabetem \(A\) to najmniejsza, w sensie inkluzji, rodzina \(\mathcal{R}\) języków zawartych w \(A^*\) taka, że:

(1) \(\emptyset \in\mathcal{R}\), \(\forall a \in A \;\;\; \{ a \} \in\mathcal{R}\)

(2) jeśli \(X, Y \in\mathcal{R}\), to \(X \cup Y, \;\; X \cdot Y \;\; \in\mathcal{R}\)

(3) jeśli \(X \in\mathcal{R}\), to \(X^* = \bigcup_{n=0} ^\infty X^n \in\mathcal{R}\)

Wprost z definicji wynika, że \(\left\{ 1\right\} =\emptyset ^{*}\in \mathcal{R}\) oraz że dla dowolnego języka regularnego zachodzi równość \(X\in \mathcal{R}\) jest

\(\displaystyle X^{+}=\bigcup ^{\infty }_{n=1}X^{n}=X\cdot X^{*}\in \mathcal{R}.\)

Wprowadzona w ten sposób definicja rodziny języków regularnych wymaga uzasadnienia faktu, iż definiowany obiekt, definiowana rodzina, istnieje. Zauważmy więc, że warunki 1-3 definicji 1.1 (patrz definicja 1.1.) spełnia na przykład rodzina \(\mathcal{P}(A^{*})\) wszystkich podzbiorów \(A^*\), a zatem klasa takich rodzin nie jest pusta. Ponadto łatwo możemy stwierdzić, że jeśli rodziny \(\mathcal{R}_{1},\: \mathcal{R}_{2}\) spełniają warunki 1-3 powyższej definicji, to rodzina \(\mathcal{R}_{1}\cap \mathcal{R}_{2}\) również spełnia te warunki. Stąd możemy wyprowadzić wniosek, że najmniejsza rodzina spełniającą te warunki, to przecięcie

\(\mathcal{REG}(A^{*})=\bigcap \mathcal{R},\)

po wszystkich rodzinach \(\mathcal{R}\) spełniających warunki 1-3 definicji 1.1. (patrz definicja 1.1.)

Zauważmy, że w świetle powyższej definicji fakt, że \(X \in\mathcal{REG}(A^{*})\) oznacza, że \(X\) można uzyskać z liter alfabetu i zbioru pustego \(\emptyset\) poprzez zastosowanie wobec tych "elementarnych klocków" skończonej liczby działań: sumy, katenacji i gwiazdkowania. Na odwrót, każdy zbiór otrzymany w ten sposób jest elementem rodziny \(\mathcal{REG}(A^{*})\). Ta obserwacja prowadzi do pojęcia wyrażeń regularnych, formalnego zapisu języków regularnych.

Definicja 1.2

Niech \(A\) będzie alfabetem, a zbiór \(\{+ , \star , \emptyset , (,)\}\) alfabetem rozłącznym z \(A\). Słowo \({\bf \alpha} \in {\bf (}A \cup \{ + , \star , \emptyset , (,)\}{\bf )}^*\) jest wyrażeniem regularnym nad alfabetem \({A}\) wtedy i tylko wtedy, jeśli:

(1) \({\bf \alpha} = \emptyset\)

(2) \({\bf \alpha} = a \in A \;\; ({\bf \alpha}\) jest literą)

(3) \({\bf \alpha}\) jest w postaci \(({\bf \beta} + {\bf \gamma}), ({\bf \beta} {\bf \gamma} ), {\bf \gamma} ^*\), gdzie \({\bf \beta}, {\bf \gamma}\)są wyrażeniami regularnymi nad alfabetem \(A\).

Przyjmujemy oznaczenia:

\(\emptyset ^{*}=1 \;\;\text{ oraz }\; \alpha ^{*}\alpha =\alpha ^{+}.\)

Rodzinę wyrażeń regularnych nad alfabetem \(A\) oznaczamy symbolem \(\mathcal{WR}\). Łatwo zauważyć związek pomiędzy wyrażeniami regularnymi oraz wprowadzoną wcześniej rodziną \(\mathcal{REG}(A^{*})\), regularnych języków wolnego monoidu \(A^{*}\). Związek ten ustala poniższa definicja.

Definicja 1.3

Wartościowaniem wyrażenia regularnego nazywamy odwzorowanie

\(|\: \: |:\mathcal{WR}\longrightarrow \mathcal{P}(A^{*})\)

określone następująco:

(1) \(\mid \emptyset \mid = \emptyset\)

(2) \(\mid a \mid = \{ a \}\)

(3) \(\mid ({\bf \alpha} + {\bf \beta})\mid = \mid {\bf \alpha} \mid \cup \mid {\bf \beta} \mid\)

           \(\mid ({\bf \alpha} {\bf \beta}) \mid = \mid {\bf \alpha} \mid \cdot \mid {\bf \beta} \mid\)

           \(\mid {\bf \alpha}^* \mid = \mid {\bf \alpha} \mid ^*\)

Odwzorowanie określające wartość wyrażenia regularnego nie jest, jak można zauważyć, iniekcją. Oznacza to, że różne wyrażenia regularne mogą mieć tę samą wartość, czyli określać ten sam język regularny. Prostym przykładem tego faktu są wyrażenia regularne \(a^*\) oraz \((a^*)^*\). Zwróćmy uwagę na wartość wyrażenia regularnego oznaczonego symbolem \(1\).

Jest mianowicie \(\mid 1 \mid = \mid \emptyset^* \mid = \mid \emptyset \mid^* = \emptyset^* = \{1\}\)

Wprowadza się następującą relację równoważności w rodzinie wyrażeń regularnych.

Definicja 1.4

Wyrażenia regularne \({\bf \alpha} , {\bf \beta}\) nazywamy równoważnymi i oznaczamy \({\bf \alpha} = {\bf \beta}\), jeśli \(\mid {\bf \alpha} \mid = \mid {\bf \beta} \mid\).

Problem równoważności wyrażeń regularnych jest rozstrzygalny i jest PSPACE-zupełny. Wrócimy do tego problemu w kolejnych wykładach.

Oto przykłady równoważnych wyrażeń regularnych

\(\begin{array}{rll} \alpha_1 + \alpha_2 & = & \alpha_2+ \alpha_1\\ (\alpha_1 + \alpha_2) +\alpha_3 & = & \alpha_1+ (\alpha_2 + \alpha_3) \\ (\alpha_1 \alpha_2) \alpha_3 & = & \alpha_1 (\alpha_2 \alpha_3) \\ (\alpha_1 + \alpha_2) \alpha_3 & = & \alpha_1\alpha_3 + \alpha_2 \alpha_3 \\ \alpha_1 ( \alpha_2 +\alpha_3) & = & \alpha_1 \alpha_2 + \alpha_1 \alpha_3 \\ (\alpha^*)^* & = & \alpha^*\\ (\alpha^*_1 \alpha^*_2)^* & = & (\alpha_1 + \alpha_2)^*\\ (\alpha^+ + 1) & = & \alpha^* \end{array}\)

gdzie \(\alpha ,\alpha _{1},\alpha _{2},\alpha _{3}\in \mathcal{WR}\).

Wprost z definicji wyrażenia regularnego wynika następujaca równoważność:

Fakt 1.1

\(L\in \mathcal{REG}(A^{*}) \Longleftrightarrow L = \mid {\bf \alpha} \mid\) dla pewnego \({\bf \alpha} \in\mathcal{WR}\).

Wyrażenia regularne dają bardzo wygodne narzędzie zapisu języków należących do rodziny \(\mathcal{REG}(A^{*})\). Np. język nad alfabetem \(\{ a,b\}\) złożony ze wszystkich słów zaczynających się lub kończących na literę \(a\) zapisujemy jako \(a(a+b)^* +(a+b)^*a\).
Z kolei wyrażenie regularne \(a^+ b^+\) oznacza język \(L=\{a^nb^m : n,m\geq 1\}\). Dla dalszego uproszczenia zapisu przyjmiemy w naszym wykładzie następującą umowę. Jeśli język \(L\) jest wartością wyrażenia regularnego \(\alpha\), czyli \(L= \mid \alpha \mid\), to będziemy zapisywać ten fakt jako \(L= \alpha\). Będziemy zatem mówić w dalszym ciągu wykładu o języku \(\alpha\). Z tych samych powodów, dla dowolnego alfabetu \(A=\{a_1,.....,a_n\}\) będziemy używać zapisu \(A\) w miejsce \(a_1 +.....+a_n\).

Zauważmy na koniec rozważań o wyrażeniach regularnych, że dość prosty w zapisie język \(L=\{a^nb^n : n\geq 1\}\) nie należy do rodziny \(\mathcal{REG}(A^{*})\) i nie można go zapisać przy pomocy wyrażeń regularnych.

Kończąc ten fragment wykładu poświęcony wyrażeniom regularnym warto wspomnieć o problemie "star height", czyli głębokości zagnieżdżenia gwiazdki w wyrażeniu regularnym. Mając wyrażenia regularne \(\alpha ,\alpha _{1},\alpha _{2}\in \mathcal{WR}\) głębokość zagnieżdżenia gwiazdki definiuje się jako liczbę \(sh(\alpha )\) równą \(0\), gdy \(\alpha\) jest literą z alfabetu lub zbiorem pustym, równą \(max\{i,j\},\) gdy \(\alpha =\alpha _{1}\cup \alpha _{2}\) lub \(\alpha =\alpha _{1}\cdot \alpha _{2}\) i \(sh(\alpha _{1})=i\), \(sh(\alpha _{2})=j\) oraz równą \(i+1\) dla \(\alpha =(\alpha _{1})^{*}\). Głębokość zagnieżdżenia gwiazdki dla języka regularnego \(L\) określa się jako najmniejszą liczbę \(sh(L)=sh(\alpha )\), gdzie \(\alpha\) jest wyrażeniem regularnym reprezentującym język \(L\). Głębokość zagnieżdżenia gwiazdki jest więc jakby miarą złożoności pętli występujących w automacie rozpoznającym język \(L\). Ustalono, że dla alfabetu złożonego z jednej litery głębokość zagnieżdżenia gwiazdki jest równa co najwyżej 1 oraz że dla alfabetu o co najmniej dwóch literach dla dowolnej liczby \(k\in \Bbb N\) można wskazać język regularny \(L\) taki, że \(sh(L)=k\). Problemem otwartym pozostaje określenie algorytmu określającego głębokość zagnieżdżenia gwiazdki dla dowolnego języka w klasie języków regularnych.

Prawa kongruencja syntaktyczna i kongruencja syntaktyczna

Opis języka regularnego za pomocą wyrażeń regularnych jest bardzo wygodny, ale nie jedyny. W kolejnych wykładach będziemy wprowadzać inne reprezentacje języków regularnych, takie jak automaty czy gramatyki. Pojęcia, które wprowadzimy teraz, są również narzędziami dla opisu i badań własności języków regularnych. W szczególności służą do konstrukcji możliwie najprostszego automatu rozpoznającego dany język regularny, zwanego automatem minimalnym.

Definicja 2.1.

Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. W monoidzie \(\; A^* \;\) wprowadzamy następujące dwie relacje:

(1) prawą kongruencję syntaktyczną \(\; P_L^r , \;\) przyjmując
dla dowolnych słów \(u, v \in A^*\)
\(u \; P_L^r \; v \;\;\) wtedy i tylko wtedy, gdy spełniony jest warunek \(\forall w \in A^* \;\; uw \in L \; \Leftrightarrow \; vw \in L,\)

(2) kongruencję syntaktyczną \(\; P_L , \;\) przyjmując
dla dowolnych \(u, v \in A^*\)
\(u \; P_L \; v \;\;\) wtedy i tylko wtedy, gdy spełniony jest warunek \(\forall w_1, w_2 \in A^* \;\; w_1uw_2 \in L \; \Leftrightarrow \; w_1vw_2 \in L.\)

Łatwo stwierdzić, że nazwy wprowadzonych relacji pokrywają się z ich własnościami, to znaczy relacja \(P_L^r\) jest rzeczywiście prawą kongruencją, a \(P_L\) kongruencją.

Przykład 2.1.

Niech \(A=\{ a,b\}\) będzie alfabetem.

(1)Dla języka \(L=a^+b^+\) relacja

(a) \(P_L^r\) ma \(4\) klasy równoważności: \(\;\;L, \;\;A^*baA^*+b^+,\;\; a^+, \;\;1\),

(b) \(P_L\) ma \(5\) klas równoważności: \(L, \;\;A^*baA^*,\;\;b^+,\;\; a^+, 1\).

(2) Dla języka \(L=\{a^nb^n : n\geq 1\}\) obie relacje mają nieskończony indeks

(a) dla \(P_L^r\) klasami równoważności są zbiory
\(L_i =\{a^nb^{n-i} : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}_0\), \(A^* \setminus\bigcup_{i=0}^\infty L_i\).

(b) dla \(P_L\) klasami równoważności są zbiory
\(L_i =\{a^nb^{n-i} : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}_0\),
\(L'_i =\{a^{n-i}b^n : n\geq i,n \geq 1\}\) dla \(i \in \mathbb{N}\),
\(A^* \setminus[\bigcup_{i=1}^\infty (L_i\cup L'_i )\cup L_0 ]\).

Udowodnimy następujące własności relacji \(\; P_L^r \;\) oraz \(\; P_L \;\).

Twierdzenie 2.1.

Prawa kongruencja syntaktyczna \(\; P_L^r \;\) jest największą w sensie inkluzji spośród wszystkich

prawych kongruencji \(\rho\) takich, że \(L = \bigcup_{w\in L}[w]_\rho\)

Kongruencja syntaktyczna \(\; P_L \;\) jest największą w sensie inkluzji spośród wszystkich

kongruencji \(\rho\) takich, że \(L = \bigcup_{w\in L}[w]_\rho\)

Dowód

Dowód przeprowadzimy dla prawej kongruencji syntaktycznej. Uzasadnienie tezy dla kongruencji \(\; P_L \;\) przebiega podobnie. Niech \(\;\rho \;\) będzie dowolną prawą kongruencją spełniającą założenia i niech \(u\rho v\). Zatem dla każdego \(w\in A^{*}\) jest

\(uw\rho vw \Rightarrow (uw\in L\Leftrightarrow vw\in L) \Leftrightarrow u\; P_L^r \; v.\)

W konsekwencji \(\rho \subseteq P_L^r.\) W szczególności więc dla dowolnego \(u \in A^*\) ma miejsce inkluzja \([u]_\rho \; \subseteq \; [u]_{P_L^r}.\) Zatem \(L\subset \bigcup _{w\in L}[w]_{P^{r}_{L}}\). Aby udowodnić inkluzję w stronę przeciwną ustalmy dowolne \(\; u \in L \;\) i niech \(v \in [u]_{P_L^r}.\) Przyjmując \(\; w =1 \;\) w definicji (patrz definicja 2.1.) relacji \(\; {P_L^r} \;\) otrzymamy równoważność \(\; u \in L \; \Leftrightarrow \; v \in L \;.\) A więc \(\; v \in L \;.\)

Wniosek 2.1.

Jeśli język \(L\) jest regularny, to relacja \(\; P_L^r \;\) jest największą w sensie inkluzji spośród wszystkich prawych kongruencji takich, że język \(L\) jest sumą jej pewnych klas równoważności, a relacja \(\; P_L \;\) jest największą w sensie inkluzji spośród wszystkich kongruencji spełniających analogiczny warunek. Obie relacje mają skończony indeks, czyli dzielą wolny monoid \(A^*\) na skończoną liczbę klas równoważności.

Pojęcie, które wprowadzimy teraz - monoid syntaktyczny języka - wiąże teorię języków formalnych, a w szczególności teorię języków rozpoznawalnych, z teorią półgrup. Związek ten stanowi podstawę dla bardziej zaawansowanych problemów teorii języków i automatów wykraczających poza ramy tego wykładu.

Definicja 2.2.

Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. Monoidem syntaktycznym języka \(\; L \;\) nazywamy strukturę ilorazową

\(M(L) = A^*/P_L .\)

Dualnie, tworząc iloraz \(S(L) = A^+/P_L\), wprowadza się pojęcie półgrupy syntaktycznej języka \(\; L \;\). Oba wprowadzone tu pojęcia zilustrowane będą w trakcie dalszych rozważań.

Automat minimalny

Określenie języka rozpoznawalnego postuluje istnienie automatu o skończonej liczbie stanów, działającego w odpowiedni sposób. Należałoby zatem wskazać algorytm budowy takiego automatu dla języka rozpoznawalnego. Oczywiście interesuje nas algorytm prowadzący do automatu o możliwie najprostszej postaci. Najprostsza postać, w tym kontekście, oznacza najmniejszą liczbę stanów.

Definicja 3.1.

Automat \(\mathcal{A} = (S,A,f,s_0,T)\) rozpoznający język \(L\) nazywamy automatem minimalnym, jeśli posiada najmniejszą liczbę stanów spośród wszystkich automatów rozpoznających język \(L.\)

Kwestią istnienia takiego automatu minimalnego zajmujemy się teraz. W kolejnym wykładzie przedstawimy algorytmy konstrukcji automatu minimalnego.

W poniższym twierdzeniu występuje automat ilorazowy \({A}_{P^{r}_{L}}\) określony przez prawą kongruencję \(P_L^r\).

Twierdzenie 3.1.

Dla dowolnego automatu \({A} = (S,A,f,s_0,T) \;\) rozpoznającego język \(\; L \subset A^* \;\) istnieje jedyny epimorfizm \(\varphi :\mathcal{A}\longrightarrow \mathcal{A}_{P^{r}_{L}}\) taki, że \(\varphi (s_{0})=[1]_{P^{r}_{L}}.\)

Dowód

Prawa kongruencja automatowa \(\sim _{\mathcal{A}}\) ma skończony indeks i \(L=\bigcup _{u\in L}[u]_{\sim _{\mathcal{A}}}\). Zatem z twierdzenia (patrz Twierdzenie 2.1.) wynika, że

\(\sim _{\mathcal{A}}\subseteq P^{r}_{L}=\sim _{\mathcal{A}_{P^{r}_{L}}}.\)

Istnienie epimorfizmu \(\; \varphi \;\) wynika z twierdzenia 1.1, wykład 3. Epimorfizm ten określony jest dla dowolnego stanu \(s\in S\) równością \(\varphi(s) = f^*([1]_{P_L^r},w) = [w]_{P_L^r},\) gdzie \(w\) jest słowem takim, że \(f(s_0,w)=s\).

Jest to jedyny epimorfizm spełniający warunki tezy dowodzonego twierdzenia. Dla każdego epimorfizmu \(\; \psi \;\) takiego, że \(\psi :\mathcal{A}\longrightarrow \mathcal{A}_{P^{r}_{L}}\) i \(\psi (s_{0})=[1]_{P^{r}_{L}}\) mamy
\(\;\forall s \in S\) \(\psi(s) = \psi(f(s_o,w)) = f^* (\psi(s_0),w) = f^* ([1]_{P_L^r},w) = [w]_{P_L^r},\)

gdzie \(f(s_0,w) = s .\) Tak więc \(\; \psi = \varphi .\)

Zatem udowodnione twierdzenie zapewnia nas o istnieniu automatu minimalnego, co formułujemy w następującym wniosku.

Wniosek 3.1.

Niech \(\; L \subset A^* \;\) będzie dowolnym językiem. Automat

\(\mathcal{A}_{P^{r}_{L}}=\left( A^{*}/_{P^{r}_{L}},A,f^{*},[1]_{P^{r}_{L}},T\right),\)

gdzie \(\; T = \{ [w]_{P_L^r} \; : \; w \in L \}, \;\) jest automatem minimalnym rozpoznającym język \(\; L \;\). Oznaczać go będziemy symbolem \(\mathcal{A}_{L}\).

Rysunek 1

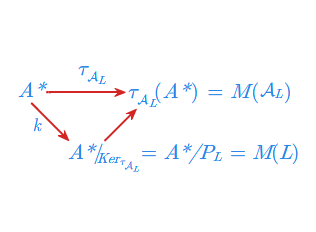
Następne twierdzenie charakteryzuje monoid przejść automatu minimalnego i podaje kolejny warunek równoważny na to, żeby język \(L\) był rozpoznawany przez automat.

Twierdzenie 3.2.

Niech \(L\subset A^{*}\) będzie dowolnym językiem.

1. Dla dowolnego języka \(L\in \mathcal{REC}(A^{*})\) monoid przejść automatu minimalnego \(\mathcal{A}_{L}\) jest izomorficzny z monoidem syntaktycznym \(M(L)\) języka \(L\), czyli

\(M(\mathcal{A}_{L})\sim M(L).\)

2. (tw. J.Myhill'a) Język \(\; L \subset A^* \;\) jest rozpoznawalny wtedy i tylko wtedy, gdy \(\; M(L) \;\) jest monoidem skończonym.

Dowód

Dla dowodu punktu 1 wykażemy, że

\(P_{L}=Ker_{\tau _{\mathcal{A}_{L}}},\)

gdzie zgodnie z definicją dla dowolnych \(w,u\in A^{*}\)

\(\tau _{\mathcal{A}_{L}}(w)([u]_{P^{r}_{L}})=f^{*}([u]_{P^{r}_{L}},w)=[uw]_{P^{r}_{L}}.\) \(\begin{array} {c} (u,w)\in Ker_{\tau _{\mathcal{A}_{L}}}\Leftrightarrow \forall v\in A^*\;\; \tau _{\mathcal{A}_{L}}(u)([v]_{P^{r}_{L}})=\tau _{\mathcal{A}_{L}}(w)([v]_{P^{r}_{L}})\Leftrightarrow [vu]_{P^{r}_{L}}=[vw]_{P^{r}_{L}}\Leftrightarrow\\ \Leftrightarrow \forall v,z \in A^*\;\;vuz\in L\Leftrightarrow vwz\in L \Leftrightarrow[u]_{P_{L}}=[w]_{P_{L}} \Leftrightarrow (u,v) \in P_L.\\ \end{array}\)

Korzystamy teraz z twierdzenia o rozkładzie epimorfizmu, które w tym przypadku ma postać: czyli \(M(\mathcal{A}_{L})\sim M(L)\).
Dla dowodu punktu 2 załóżmy, że język \(\; L \;\) jest rozpoznawalny. Zatem

\(L = \bigcup_{w \in L} [w]_\rho ,\) gdzie \(\; \rho \;\) jest kongruencją o skończonym indeksie.

Z twierdzenia (patrz twierdzenie 2.1.) wnioskujemy, że \(\rho \subseteq P_L .\) Oznacza to, że indeks relacji \(\; P_L \;\) jest niewiększy od indeksu \(\; \rho, \;\) a co za tym idzie, \(\; M(L) = A^*/P_L \;\) jest monoidem skończonym.

Dla dowodu implikacji w stronę przeciwną rozważmy epimorfizm kanoniczny \(k : A^* \longrightarrow A^*/P_L = M(L).\) Pokażemy, że spełnia on warunki z punktu 4. twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2. wykład 3). \(M(L) \;\) jest skończony, więc pozostaje do wykazania

równość

\(\; L = k^{-1}(k(L)). \;\) W tym celu wystarczy oczywiście udowodnić inkluzję \(\; k^{-1}(k(L)) \subseteq L\).

\(\begin{array} {c} v \in k^{-1}(k(L))\Rightarrow k(v) \in k(L)\Rightarrow\exists u \in L:k(v) = k(u) \in k(L)\Leftrightarrow\\ \Leftrightarrow \exists u \in L:[v]_{P_L} = [u]_{P_L}\Leftrightarrow\exists u \in L:v \in L\Leftrightarrow u\in L.\\ \end{array}\) Czyli \(v\in L\) i \(\; L = k^{-1}(k(L))\).

Z twierdzenia 3.1 (patrz twierdzenie 3.1.) wynika, że określenie klas abstrakcji prawej kongruencji syntaktycznej \(P^r_L\) prowadzi do określenia minimalnego automatu rozpoznającego język \(L\). Prezentowane poniżej twierdzenia wskazują sposób konstrukcji prawej kongruencji syntaktycznej dla języka \(L\).

Twierdzenie 3.3.

Niech \(\; L \subset A^* \;\) będzie dowolnym językiem,
a \(\; \Theta_L \subset A^* \times A^* \;\) relacją równoważności o dwóch klasach równoważności \(L\) i \(A^* \setminus L\). Przez \(\; \rho_i \;\) dla \(\; i \in {\Bbb N}\) oznaczmy zstępujący ciąg relacji określony następująco:

\(\rho_1 = \Theta_L ,\;\;\) a dla \(\; i = 2,...\) przyjmijmy

\(\rho_i = \{ (u,w) \in \; A^* \times A^* \; : \; (ua,wa) \in \; \rho_{i-1} \;\;\; \forall a \in A \cup \{1\}\}.\)

Wtedy \(\;\; \bigcap \rho_i = P_L^r \;\;\).

Dowód

Na początku uzasadnimy, że \(\; \bigcap \rho_i \;\) jest prawą kongruencją na \(\; A^*\). Załóżmy więc, że słowa \(\; x , y \in A^* \;\) są w relacji \(x \; \bigcap \rho_i \;y \;\). Wybierzmy dowolne słowo \(z\in A^{*}\) i niech \(k\) oznacza długość tego słowa. Z założenia wynika, iż \(x\, \rho _{i+k}\, y\), co w świetle definicji ciągu relacji \(\rho _{i}\) implikuje, że \(xz\: \rho _{i}\: yz.\) Ponieważ \(i\) jest dowolne wnioskujemy ostatecznie, że \(xz \; \bigcap \rho_i \; yz \;,\) co kończy dowód faktu, że \(\; \bigcap \rho_i \;\) jest prawą kongruencją.

Dowiedziemy teraz równości \(\bigcap \rho_i \; = \; P_L^r .\)

Dla uzasadnienia inkluzji \(\bigcap \rho_i \;\subseteq\; P_L^r\) zauważmy, że jeśli \(x \; \bigcap \rho_i \; y ,\) to dla dowolnego \(z\in A^{*}\) mamy \(xz \; \bigcap \rho_i \; yz\), a w szczególności \(xz \; \rho_1 \; yz.\) Z definicji relacji \(\rho _{1}\) dla dowolnego \(z\in A^{*}\) prawdziwa jest równoważność

\(xz \in L \;\; \Leftrightarrow \;\; yz \in L.\)

A więc \(x \;\; P_L^r \;\; y\). Inkluzję w stronę przeciwną pokażemy, dowodząc indukcyjnie ze względu na \(i=1,2,...,\) że dla dowolnych \(\;x , y \in A^* \;\) prawdziwa jest następująca implikacja

\(x \;\; P_L^r \;\; y \;\;\; \Longrightarrow \;\;\; x \; \rho_i \; y \;\;.\)

Załóżmy zatem, że \(x \;\; P_L^r \;\; y.\) Z definicji \(\; P_L^r \;\) wynika, że dla dowolnego \(z \in A^*\) prawdziwa jest równoważność

\(xz \in L \;\; \Leftrightarrow \;\; yz \in L.\)

Przyjmując \(\; z=1 \;\) otrzymujemy żądaną własność dla \(\rho _{1}.\) Załóżmy teraz, że prawdziwa jest implikacja

\(x \;\; P_L^r \;\; y \;\;\; \Longrightarrow \;\; x \; \rho_i \; y.\)

dla \(i = 1,...,n-1\) oraz dla dowolnych \(x , y \in A^*.\) Stąd, że \(P_L^r\) jest prawą kongruencją, wnioskujemy, że dla dowolnego \(\; a \in A \cup \{1\} \;\) spełniona jest relacja \(xa \;\; P_L^r \;\; ya.\) Korzystając z założenia indukcyjnego, mamy \(xa \;\; \rho_{n-1} \;\; ya\) dla dowolnego \(\; a \in A \cup \{1\} \;\). A to oznacza z definicji \(\; \rho_i \;\), że \(x \;\; \rho_n \;\;y\) i kończy dowód.

Kolejne twierdzenie charakteryzuje relację \(P^r_L\) dla języka rozpoznawalnego i orzeka, iż w przypadku języka rozpoznawalnego ciąg relacji \(\rho_i\), aproksymujacych \(P^r_L\), jest skończony. Równoważność dwóch pierwszych warunków poniższego twierdzenia nazywana bywa często w literaturze twierdzeniem A.Nerode.

Twierdzenie 3.4.

Następujące warunki są równoważne:

(1) Język \(L\) jest rozpoznawalny.

(2) Relacja \(P^r_L\) ma skończony indeks.

(3) Ciąg relacji \(\rho_i\) stabilizuje się, co oznacza, że istnieje \(i\in {\Bbb N}\) takie, że \(\rho_i = \rho_{i+1}=....\)Dla najmniejszego takiego \(i\) prawdziwa jest równość \(\rho_i = P^r_L.\)

Dowód

Dowód poprowadzimy według następujacego schematu:

\(1 \Longleftrightarrow 2 \Longleftrightarrow 3\)

\(1 \Longrightarrow 2\)

\(P^r_L\) jest największą w sensie inkluzji relacją spełniająca warunki punktu 2 z twierdzenia 1.3 z wykładu 3 (patrz twierdzenie 1.2 wykład 3). Z tego samego twierdzenia wynika skończoność indeksu.

\(1 \Longleftarrow 2\)

Relacja \(P^r_L\) jest prawą kongruencją, ma skończony indeks oraz

\(L = \bigcup \limits_{w \in L}[w]_{P^r_L}.\)

Z twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2 wykład 3) wynika więc, że język \(L\) jest rozpoznawalny.

\(2 \Longrightarrow 3\) Dowód poprowadzimy nie wprost. Załóżmy więc, że dla każdego \(i\in {\Bbb N}\) jest \(\rho_i \neq \rho_{i+1}.\) Oznacza to, że dla każdego \(i\in {\Bbb N}\) indeksy relacji \(\rho _{i}\) tworzą ciąg silnie rosnący, to znaczy spełniają zależność \(ind\rho_i < ind\rho_{i+1}.\) Ponieważ \(ind\rho_1 = 2,\) to dla każdego \(i\in {\Bbb N}\) prawdziwa jest nierówność \(ind\rho_i > i.\) A to prowadzi do wniosku, że dla dowolnego \(i\in {\Bbb N}\)

\(indP^r_L = ind\bigcap\rho_i >i .\)

Zatem indeks relacji \(P^r_L\) jest nieskończony, co jest sprzeczne z założeniem.

\(2 \Longleftarrow 3\)

Udowodnimy indukcyjnie ze względu na \(j\), że każda z relacji \(\rho_j\) dla \(j=1,...,i\) ma skończony indeks. Oczywiście \(ind\rho_1 = 2.\) Załóżmy teraz, że relacja \(\rho_j\) ma skończony indeks. Z definicji relacji \(\rho_{j+1}\) wynika, że jej klasy równoważności powstają przez podział klas równoważności \([w]_{\rho_j}\) na skończoną liczbę klas relacji \(\rho_{j+1}\) (skończona jest liczba możliwych do spełnienia warunków prowadzących do podziału). Oznacza to, że indeks relacji \(\rho_{j+1}\) jest również skończony, a więc relacja \(P^r_L\) ma również skończony indeks.

Wykorzystamy powyżej udowodnione własności do konstrukcji automatu minimalnego rozpoznającego język \(L\). Warto zauważyć, iż punktem wyjścia dla tej konstrukcji jest język \(L\) zadany, na przykład, poprzez wyrażenie regularne.

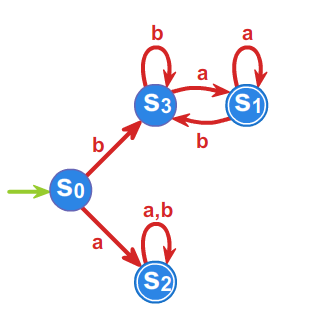
Przykład 3.1.

Niech do języka \(L\) należą wszystkie słowa nad alfabetem \(A=\{a,b\}^*\) zaczynające się lub kończące literą \(a\). Skonstruujemy minimalny automat akceptujący język \(L\).

\(\rho _{1}:\) \(L=aA^* +A^* a,\;\; A^{*}\setminus L =bA^*b +b+1\)

\(\rho _{2}:\) \(aA^*a+a,\;\; bA^*a, \;\; bA^*b +b+1,\)

\(\rho _{3}:\) \(aA^*a+a,\;\; bA^*a, \;\; bA^*b +b, \;\;1,\)

Ponieważ \(\rho _{3}=\rho _{4}\), to \(P^r_L=\rho _{3}\) i automat minimalny ma \(4\) stany.
Przyjmujemy \(s_0 =[1]\), \(s_1=bA^*a\), \(s_2=aA^*a+a\), \(s_3=bA^*b +b\) oraz \(T=\{s_1,s_2\}\), a automat minimalny \(\mathcal{A}_{L}=\left( A^{*}/_{\rho _{3}},f^{*},s_{0},T\right)\)

przedstawiony jest przy pomocy grafu: Rysunek 2

Przykład 3.2.

Dla języka \(L=\left\{ w \in \{ a,b\}^* :\#_a w =2k, \#_b w =2l+1 ,\; k,l\geq 0 \right\}\) określimy ciąg relacji \({\rho}_i\), a następnie relację \(P^{r}_{L}\). Umożliwi nam to, w świetle powyższych rozważań, zbudowanie automatu minimalnego rozpoznającego ten język. Poniżej wypisane są klasy równoważności relacji \(\rho _{1}\) oraz \(\rho _{2}\), \(\rho _{3}=\rho _{2}\), co kończy proces obliczania relacji \(\rho _{i}\) i daje równość \(\rho _{2}=P^{r}_{L}\).

\(\rho _{1}:\) \(L, A^{*}\setminus L\)

\(\rho _{2}:\) \(L, L_1, L_2, L_3\), gdzie
\(L_1=\left\{ w \in \{ a,b\}^* :\#_a w =2k, \#_b w= 2l, \; k,l\geq 0 \right\},\)
\(L_2\left\{ w \in \{ a,b\}^* :\#_a w =2k+1, \#_b w= 2l+1, \; k,l\geq 0 \right\},\)
\(L_3=\left\{ w \in \{ a,b\}^* :\#_a w =2k+1, \#_b w= 2l, \; k,l\geq 0 \right\},\)

Przyjmując \(s_0 =L_1=[1]\), \(s_1=L_3\), \(s_2=L_2\), \(s_3=L\) oraz \(T=\{s_3\}\)

automat minimalny \(\mathcal{A}_{L}=\left( A^{*}/_{\rho _{2}},f^{*},s_{0},T\right)\) przedstawiony jest przy pomocy grafu: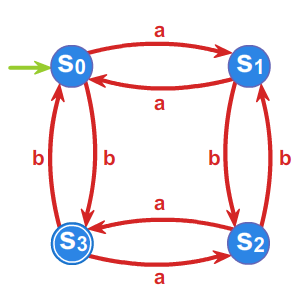 Rysunek 3

Powyższe twierdzenia podają również sposób konstrukcji monoidu syntaktycznego języka \(L\).