Informatyka MIMUW

Algorytm Hoare'a w pesymistycznym przypadku może wymagać bardzo długiego czasu działania. Możemy tak zmodyfikować poprzedni algorytm, aby zapewnić liniowy czas działania nawet w najgorszym przypadku.

Kluczem do nowego algorytmu jest lepszy wybór elementu dzielącego (zmienna m z 5-linii algorytmu Hoare'a). Element ten jest obliczany w następujący sposób:

• dzielimy ciąg $A$ na podciągi 5-elementowe $P_1,\ldots,P_{\lceil |A|/5 \rceil}$,

• każdy z podciągów sortujemy, otrzymując $P'_1,\ldots,P'_{\lceil |A|/5 \rceil}$,,
• wybieramy z każdego podciągu 3-ci co do wielkości element otrzymując krótszy ciąg $M$,

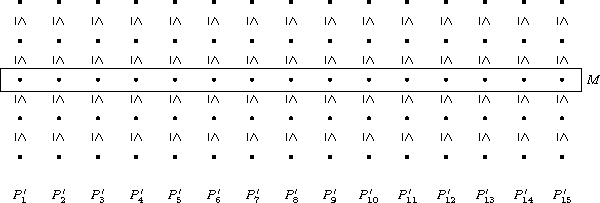
• jako m wybieramy medianę ciągu $M$ (którą to obliczamy rekrurencyjnie).

Dzięki takiemu znacznie bardziej skomplikowanemu wyborowi możemy zagwarantować bardziej równomierny podział ciągu $A$ na podciągi elementów mniejszych ($A_{ < }$), oraz większych ($A_{>}$) od m.

Algorytm

function AlgorytmMagicznychPiatek(A[1..n], k);
begin
  if n<=10 then
    posortuj tablicę A 
    return A[k] 
  else begin
    podziel elementy z tablicy A na podciągi 5-elementowe:  P(1),...,P(n/5) 
    (jeśli n nie jest wielokrotnością 5, uzupełnij ostatni podciąg wartościami infty)
    Niech M={ P_i [3] : 1 <= i <= n/5}  (zbiór median ciągów P(i));
    m:=AlgorytmMagicznychPiatek(M, ceil(|M|/2));
    A_< :={ A[i] : A[i]  <  m};
    A_= :={ A[i] : A[i] = m}; 
    A_> :={ A[i] : A[i] > m};
    if |A_<| <= k  then return AlgorytmMagicznychPiatek(A_<,k)
    else  if |A_< |+|A_=| <= k  then return m 
    else return AlgorytmMagicznychPiatek(A_>,  k-|A_<|-|A_=|); 
  end
end

Analiza złożoności czasowej

Na pierwszy rzut oka algorytm wygląda bardzo podobnie do algorytmu Hoare'a. Nowy algorytm jest jednak znacznie bardziej efektywny: nawet w pesymistycznym przypadku algorytm kończy działanie po $O(n)$ krokach.
Złożoność algorytmu możemy opisać następującym równaniem rekurencyjnym.

• rozmiar zbioru |M| możemy ograniczyć przez $\lceil n/5 \rceil$
• ze względu na dodatkowy czas poświęcony na obliczanie mediany m, możemy podać lepsze ograniczenia na rozmiary zbiorów $A_{ < },\ A_{>}$: