Drzewa AVL
W drzewach poszukiwań binarnych (BST, od ang. Binary Search Tree) pesymistyczny koszt wymienionych wyżej operacji słownikowych jest proporcjonalny do wysokości drzewa. Kształt drzewa - więc i jego wysokość - zależy od ciągu wykonywanych na nim operacji. Nietrudno podać przykład ciągu operacji konstruującego drzewo o \( n \) węzłach i wysokości \( \Theta(n) \). W drzewach AVL (Adelson-Velskij, Landis [AVL]) do warunku BST umożliwiającego wyszukiwanie w czasie proporcjonalnym do wysokości drzewa, dołożono warunek zrównoważenia, gwarantujący, że wysokość drzewa zawsze pozostaje logarytmiczna względem jego rozmiaru:
W każdym węźle wysokości obu jego poddrzew różnią się co najwyżej o 1.
W każdym węźle przechowywany jest dodatkowy atrybut, "współczynnik zrównoważenia", przyjmujący wartości:
"-" jeśli lewe poddrzewo jest o 1 wyższe niż prawe;
"0" jeśli oba poddrzewa są takiej samej wysokości;
"+" jeśli prawe poddrzewo jest o 1 wyższe niż lewe.
Jako ćwiczenie pozostawiamy dowód faktu, że drzewo AVL o \( n \) węzłach ma wysokość \( O(\log n) \).
Pokażemy teraz, jak wykonywać wszystkie operacje słownikowe na drzewach AVL z kosztem co najwyżej proporcjonalnym do wysokości drzewa (czyli logarytmicznym). Operacja Find jest wykonywana tak samo jak w zwykłych drzewach BST: schodzimy w dół drzewa po ścieżce od korzenia do szukanego węzła (albo do węzła zewnętrznego NULL), o wyborze lewego lub prawego poddrzewa na każdym poziomie rozstrzygając na podstawie porównania szukanego klucza z zawartością aktualnego węzła na ścieżce. Operacje Insert i Delete są bardziej skomplikowane, ponieważ wymagają aktualizowania współczynników zrównoważenia, a niekiedy również przywracania warunku AVL.
Rotacje
Do zmiany kształtu drzewa w celu jego zrównoważenia służy mechanizm rotacji. Po wykonaniu rotacji pojedynczej ROT1\( (p,q) \) węzła \( p \) z jego ojcem \( q \) oba węzły zamieniają się rolami ojciec-syn, przy zachowaniu własności BST:
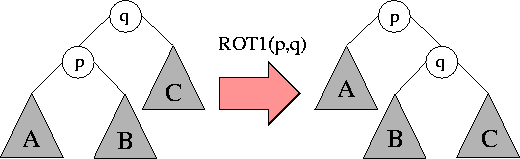
(symetryczny przypadek, w którym \( p \) jest prawym synem \( q \), stanowi lustrzane odbicie powyższego).
W rotacji podwójnej ROT2(p,q,r) uczestniczą trzy węzły: \( p \), jego ojciec \( q \) i jego dziadek \( r \), przy czym albo \( p \) jest lewym synem, a \( q \) prawym (ten właśnie przypadek jest zilustrowany poniżej), albo odwrotnie. Po rotacji \( p \) staje się korzeniem całego drzewa, przy zachowaniu własności BST:
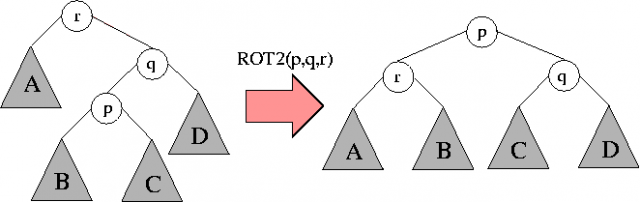
Nietrudno zauważyć, że rotacja podwójna ROT2(p,q,r) jest w rzeczywistości złożeniem dwóch rotacji pojedynczych ROT1(p,q) i ROT1(p,r). Koszt wykonania jednej rotacji jest stały.