Informatyka MIMUW

Podczas operacji Insert tak samo jak dla zwykłych drzew BST schodzimy po ścieżce od korzenia w dół do węzła zewnętrznego NULL i w jego miejscu tworzymy nowy liść ze wstawianym kluczem. Następnie wracamy po ścieżce do korzenia, aktualizując współczynniki zrównoważenia. Jeśli stwierdzamy, że wysokość aktualnie rozważanego poddrzewa nie zmieniła się w stosunku do sytuacji przed wykonaniem Insert, to kończymy operację, a jeśli stwierdzamy, że wysokość poddrzewa wzrosła (mogła wzrosnąć co najwyżej o 1!), kontynuujemy marsz w górę drzewa. Jeśli w wyniku wzrostu wysokości jednego z poddrzew aktualnie rozważanego węzła został w nim zaburzony warunek AVL, to przywracamy go za pomocą rotacji. Z dokładnością do symetrii mamy wtedy dwa przypadki (w obydwu zakładamy, że \( p \) jest węzłem, w którym zaburzony został warunek AVL wskutek wzrostu wysokości jego prawego poddrzewa o korzeniu \( q \); w pierwszym przypadku zakładamy, że wzrosła wysokość prawego poddrzewa \( q \), a w drugim - lewego).

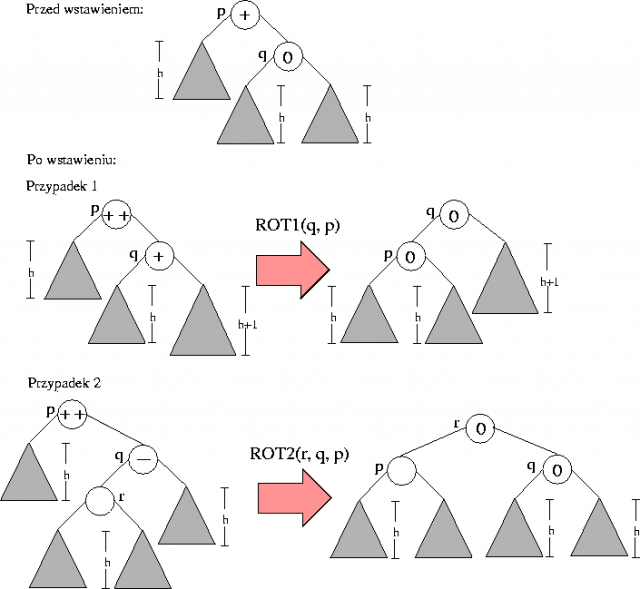
Zauważmy, że w obydwu przypadkach po rotacji wysokość całego poddrzewa jest taka sama jak przed całą operacją, zatem wykonanie jednej rotacji (pojedynczej lub podwójnej) kończy operację Insert.

Poniższa animacja ilustruje przykładową historię wstawiania do drzewa AVL.

Operację Delete, tak samo jak w przypadku usuwania ze zwykłego drzewa BST, sprowadzamy do przypadku usuwania węzła mającego co najwyżej jednego syna. Zauważmy, że w drzewie AVL albo sam węzeł, albo jego jedyny syn musi być liściem. Po usunięciu węzła wracamy po ścieżce do korzenia, aktualizując współczynniki zrównoważenia. Jeśli stwierdzamy, że wysokość aktualnie rozważanego poddrzewa nie zmieniła się w stosunku do sytuacji przed wykonaniem Delete, kończymy operację, a jeśli stwierdzamy, że wysokość poddrzewa spadła (mogła spaść co najwyżej o 1!), to kontynuujemy marsz w górę drzewa. Jeśli w wyniku spadku wysokości jednego z poddrzew aktualnie rozważanego węzła został w nim zaburzony warunek AVL, to przywracamy go za pomoca rotacji. Z dokładnością do symetrii mamy wtedy dwa przypadki (w obydwu zakładamy, że \( p \) jest węzłem, w którym zaburzony został warunek AVL wskutek spadku wysokości jego lewego poddrzewa, a \( q \) jest korzeniem prawego poddrzewa \( p \); w pierwszym przypadku zakładamy, że współczynnik zrównoważenia w \( q \) przed operacja Delete był równy "0" lub "+", a w drugim, że "-").

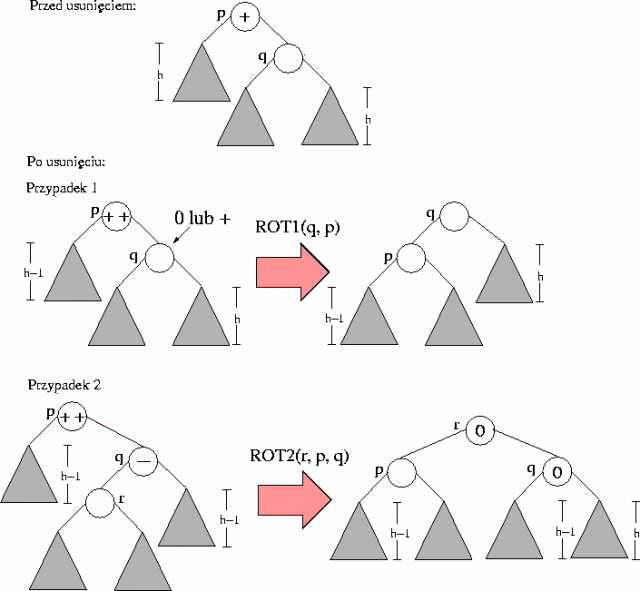
W pierwszym przypadku, jeśli współczynnik zrównoważenia w \( q \) przed operacją Delete był równy "0", po rotacji wysokość całego poddrzewa jest taka sama jak przed całą operacją, wykonanie rotacji kończy więc operację Delete. Jeśli jednak współczynnik był równy "+", wysokość spada o 1. W przypadku 2 wysokość całego poddrzewa również spada o 1 i trzeba kontynuować marsz w stronę korzenia. Operacja Delete może zatem wymagać wykonania logarytmicznej liczby rotacji. Poniższa animacja ilustruje operację usuwania elementu z drzewa AVL.