Informatyka MIMUW

Pokażemy pewne proste zastosowanie tablic prefikso-sufiksów. Słowem pokrywającym tekst x jest każdy taki tekst y, którego wystąpienia w x pokrywają cały tekst x. Na przykład słowo y=aba pokrywa tekst x=ababaaba, natomiast nie pokrywa tekstu abaaababa. Zajmiemy się problemem: obliczyć w czasie liniowym długość najkrótszego słowa pokrywającego dany tekst x.

Niech \( S[i] \) będzie rozmiarem minimalnego słowa pokrywającego tekst \( x[1..i] \).

Następujący algorytm oblicza długość minimalnego słowa pokrywającego tekstu x. Algorytm jest efektywny ponieważ liczy dodatkową tablicę Zakres. W \( i \)-tej iteracji algorytmu pamiętany jest znany dotychczas zakres każdego minimalnego słowa pokrywającego.

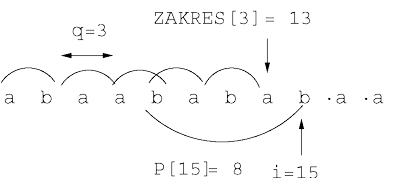
Rysunek 1: \( i \)-ta iteracja algorytmu dla \( i=15 \) oraz słowa \( x\ =\ abaabababaababa\ldots \). Tuż przed rozpoczęciem tej iteracji mamy \( P[i]=8 \), \( S[8]=2,\ Zakres[3]=13 \). Zatem spełniony jest warunek \( i-Zakres[S[P[i]] \le S[P[i]] \). Po zakończeniu \( i \)-tej iteracji mamy \( S[15]=3,Zakres[3]=15 \).

Algorytm Rozmiar-Minimalnego-Pokrycia

for i:=2 to n do begin
    Zakres [i]=i; S [i]=i;
end;
for i:=2 to n  do
    if P [i]>0 and i-Zakres[S[P[i]]] <= S[P[i]] then begin
      S[i] :=S[P[i]]; Zakres[S[P[i]] :=i
    end;
return S[n];