Informatyka MIMUW

Algorytm MP wykonuje co najmniej 2n-m porównań symboli. Załóżmy, że są to operacje dominujące i spróbujmy zmniejszyć stały współczynnik 2 do \( \frac{3}{2} \). Na początku załóżmy, że \( x=ab \). Następujący algorytm znajduje wszystkie wystąpienia wzorca ‘’ab’’ w tekście y.

Algorytm Szukanie-ab

wzorcem jest ab
i:=0; 
while i <= n-m do begin 
while y[i+2] <> b do i=i+1; 
if y[i+1]= a then 
wypisz-wystąpienie;i := i+2 
end;

Algorytm MP dla wzorca ‘’ab’’ i tekstu ‘’aaa...aa’’ wykonywał 2n-2 porównań symboli, nowy algorytm jest lepszy. Algorytm Szukanie-ab wykonuje co najwyżej n porównań w tym przypadku. Dla tekstu ‘’abab’’ algorytm wykinuje n+1 porównań.

Pozostawiamy jako ćwiczenie policzenie maksymalnej liczby porównań dla tego algorytmu (wzorzec ‘’ab’’). Widać, że podstawowa idea to sprawdzanie najpierw pierwszego symbolu wzorca różnego od poprzednich.

Uogólnimy algorytm na dowolne wzorce. Niech x zawiera co najmniej dwa różne symbole, \( x=a^kb\alpha \), gdzie \( a\ne b \).Oznaczmy \( x'=b\alpha \) skrócony wzorzec

Przykład

\( x\ =\ aaaabaaaababa \), wtedy \( x'\ =\ baaaababa \), \( \alpha\ =\ aaaababa \).

Podamy nieformalny zarys działania oszczędniejszej wersji algorytmu MP, w której osobno szukamy x' i osobno części \( a^k \).

Niech \( MP' \) będzie taką wersją algorytmu MP, w której szukamy jedynie wzorca \( x' \), ale tablica \( P \) jest obliczona dla wzorca \( x \). Jeśli \( j>0 \) i \( shift\le k \), to wykonujemy przesunięcie potencjalnego początku i wzorca w y o k+1, gdzie \( shift=j-P[j] \).

Inaczej mówiąc, nie szukamy wszystkich wystąpień x', ale jedynie takich, które mają sens z punktu widzenia potencjalnego znalezienia na lewo ciągu \( a^k \).

Tak zmodyfikowany algorytm MP zastosujemy jako część algorytmu Oszczędny-MP. Graficzna ilustracja działania algorytmu Oszczędny-MP jest pokazana na rysunku.

Algorytm Oszczędny-MP
Znajdujemy wystąpienia x' w tekście \( y[k+1..m] \) algorytmem MP';

dla każdego wystąpienia x' sprawdzamy, czy na lewo jest wystąpienie \( a^k \);
nie sprawdzamy tych pozycji w y, których zgodność z pewną pozycją w x jest znana;

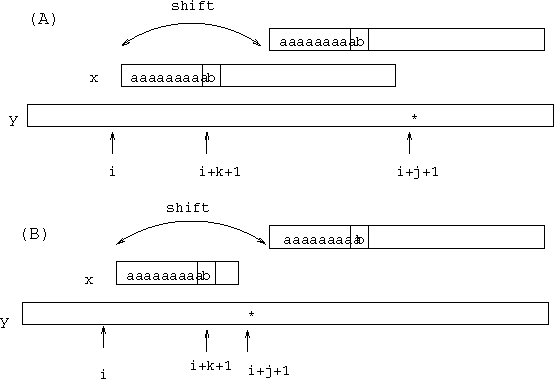
Rysunek 3:Typowa konfiguracja w algorytmie Oszczędny-MP.

Pozostawiamy jako ćwiczenie dokładny zapis algorytmu oraz dokładniejszy dowód tego, że algorytm Oszczędny-MP wykonuje co najwyżej \( \frac{3}{2}n \) porównan.
Ogólna idea jest przedstawiona na rysunku.

Rysunek 4: Ilustracja tego, że liczba operacji dodatkowych jest ograniczona przez \( \frac{1}{2}n \).

Niech zasadniczymi operacjami będą operacje sprawdzania pierwszego b na danej pozycji tekstu y oraz te sprawdzania symboli, które są z wynikiem pozytywnym. Takich operacji jest co najwyżej n. Pozostałe operacje to

(1) sprawdzanie w części \( \alpha \) z wynikiem negatywnym; wtedy przesuwamy wzorzec co najmniej o k,

(2) sprawdzanie części \( a^k \) na lewo od pozytywnego \( b \) (w kwadraciku na rysunku), na pozycjach, gdzie wcześniej było sprawdzanie negatywnego b. Wtedy odległość między pozytywnymi kolejnymi b jest co najmniej 2w, gdzie \( w\le k \) jest liczbą sprawdzanych na lewo symboli a. Zatem ‘’lokalnie’’ przesunięcie jest co najmniej dwukrotnie większe niż liczba dodatkowych operacji.

Suma przesunięć wzorca na tekście \( y \) wynosi co najwyżej n, sumaryczna liczba dodatkowych operacji jest więc co najwyżej \( \frac{1}{2}n \), a liczba wszystkich operacji nie przekracza \( \frac{3}{2}n \).