Ćwiczenia 17: Imperatywne wskaźnikowe struktury danych

Zaimplementuj kolejki FIFO+LIFO jako imperatywne listy dwukierunkowe.
Dana jest definicja typu elementów tworzących listy wskaźnikowe:
```
      type 'a option = None | Some of 'a
      type 'a elem = {v: 'a; mutable next: 'a lista}
      and  'a lista = 'a elem option
 
```
1. Napisz procedurę $\mathtt{petla}: \mathtt{lista} \to \mathtt{unit}$, która mając daną listę jednokierunkową, tworzy z niej listę cykliczną, ale z odwróconym kierunkiem wskaźników.
  Możesz założyć, że dana lista jest poprawną listą jednokierunkową, to znaczy ma koniec i nie zapętla się.
  
  Rozwiązania
2. Napisz procedurę $\mathtt{przeplot}: \mathtt{lista} \to \mathtt{lista} \to \mathtt{unit}$, która splata obie listy w jedną listę postaci: pierwszy rekord pierwszej listy, pierwszy rekord drugiej listy, drugi rekord pierwszej listy, drugi rekord drugiej listy, itd. Jeśli jedna z list jest dłuższa, to jej końcówka stanowi końcówkę listy wynikowej.
  
  Rozwiązania
Napisz procedurę tworzącą cykliczną listę modyfikowalną.
Dane są deklaracje typów:
```
      type elem = { x: int; mutable prev: elem list };;
      type lista = elem list;;
 
```
Napisz procedurę $\mathtt{ustaw} : \mathtt{lista} \to \mathtt{unit}$, która dla danej listy $[x_1; x_2; \dots; x_n]$ typu lista, tak ustawia pola prev, aby (dla $i=1,2,\dots, n$) prowadziło ono z elementu $x_i$ do listy zaczynającej się w elemencie $x_{n-i+1}$.
[XII OI, Skarbonki]
Mamy $n$ skarbonek otwieranych kluczykami.
Do każdej skarbonki jest inny kluczyk.
Kluczyki do skarbonek są powrzucane do skarbonek.
Żeby dostać się do zawartości skarbonki, skarbonkę można otworzyć kluczykiem (jeśli się go ma) lub ją rozbić.

Skarbonki są ponumerowane od 0 do $n-1$.
Na podstawie tablicy $a$ (rozmiaru $n$), takiej, że $a.(i) = $ numer skarbonki, w której znajduje się kluczyk do skarbonki
numer $i$, oblicz minimalną liczbę skarbonek, które należy rozbić, tak aby dostać się do zawartości wszystkich skarbonek.
[X OI, Małpki]
Na drzewie wisi $n$ małpek ponumerowanych od 1 do $n$.
Małpka z nr 1 trzyma się gałęzi ogonkiem.
Pozostałe małpki albo są trzymane przez inne małpki, albo trzymają się innych małpek, albo jedno i drugie równocześnie.
Każda małpka ma dwie przednie łapki, każdą może trzymać co najwyżej jedną inną małpkę (za ogon).
Rozpoczynając od chwili 0, co sekundę jedna z małpek puszcza jedną łapkę.
W ten sposób niektóre małpki spadają na ziemię, gdzie dalej mogą puszczać łapki (czas spadania małpek jest pomijalnie mały).

Zaprojektuj algorytm, który na podstawie opisu tego która małpka trzyma którą, oraz na podstawie opisu łapek puszczanych w
kolejnych chwilach, dla każdej małpki wyznaczy moment, kiedy spadnie ona na ziemię.
Na szachownicy jest ustawionych $n$ wież, które należy pokolorować.
Jeśli dwie wieże się atakują (są w tej samej kolumnie lub wierszu), to muszą być tego samego koloru.
Napisz procedurę kolory: int * int list → int,
która na podstawie listy współrzędnych wież wyznaczy maksymalną liczbę kolorów, których można użyć kolorując wieże.
Podaj złożoność czasową i pamięciową swojego rozwiązania.
Dana jest prostokątna mapa złóż gazu wraz z odwiertami pobierającymi gaz. Mapa jest dana w postaci dwuwymiarowej prostokątnej tablicy liczb całkowitych. Miejsca odwiertów są zaznaczone liczbami ujemnymi. Wartość bezwzględna elementu tablicy oznacza ilość znajdującego się w danym miejscu gazu.

Pola niezerowe stykające się bokami tworzą jedno złoże. Odwierty znajdujące się w danym złożu pozwalają pobrać tyle gazu ile pól obejmuje złoże, po czym ilość gazu we wszystkich polach złoża maleje o 1. Może to spowodować zmniejszenie lub podzielenie się złoża. Dalej odwierty pozwalają pobierać gaz z tak zmienionych złóż.

Napisz procedurę $\mathtt{gaz}: \mathtt{int~array~array} \to \mathtt{int}$, która obliczy łączną ilość gazu, jaką wydobędą odwierty.
Dana jest plansza podzielona na sześciokątne pola, o wymiarach $n \times n$ (patrz rysunek).
$i$-te pole w $j$-tym rzędzie sąsiaduje z polami:
- $i-1$ i $i$ w rzędzie $j-1$,
- $i-1$ i $i+1$ w rzędzie $j$,
- $i$ i $i+1$ w rzędzie $j+1$.
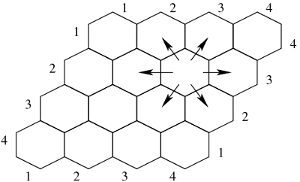Plansza do gry Hex

Dwaj gracze, biały i czarny, grają w grę hex.
Zajmują oni na przemian wolne pola na planszy. Zaczyna gracz biały.
Gracz biały stara się połączyć swoimi polami lewy i prawy brzeg planszy, a gracz czarny górny i dolny brzeg planszy.
Wygrywa gracz, który jako pierwszy połączy odpowiednie brzegi planszy, w ten sposób, że z jednego brzegu na drugi
będzie można przejść przez sąsiadujące pola zajęte przez danego gracza.

Napisz procedurę hex : int → (int * int) list → (bool * int), która na podstawie wielkości planszy $n$,
oraz listy współrzędnych (rząd, pozycja w rzędzie) kolejno zajmowanych przez graczy pól określi, czy wygrał gracz biały
(true), czy czarny (false) i w którym ruchu.
[XIV OI, Biura]
W firmie pracuje $n$ pracowników ponumerowanych od $1$ do $n$.
Każdy pracownik otrzymał służbowy telefon, w którym ma zapisane numery telefonów niektórych swoich współpracowników
(a wszyscy ci współpracownicy mają w swoich telefonach zapisany jego numer).
W związku z dynamicznym rozwojem firmy zarząd postanowił przenieść siedzibę firmy do nowych biurowców.
Postanowiono, że każda para pracowników, którzy będą pracować w różnych budynkach, powinna znać (nawzajem) swoje
numery telefonów, tzn. powinni oni mieć już zapisane nawzajem swoje numery w służbowych telefonach komórkowych.
Równocześnie, zarząd postanowił zająć jak największą liczbę biurowców.

Napisz procedurę biura : int → int * int list → int, która na podstawie liczby pracowników $n$ oraz listy par pracowników
posiadających nawzajem swoje numery telefonów $l=[(a_1,b_1);\dots; (a_m,b_m)]$, wywołana jako $\mathtt{biura}\ n\ l$, obliczy liczbę biurowców.

Rozwiązując to zadanie przyjmij, że $m=O(n)$.
[ONTAK 2007]
Wyobraźmy sobie ciąg zer i jedynek $(x_1, x_2, \dots, x_n)$.
Mamy dany ciąg trójek postaci $(i, j, s)$, gdzie $i$ i $j$ są indeksami w ciągu $(x_i)$, $1 \le i \le j \le n$,
natomiast $s = (\sum_{k=i}^j x_k) \mod 2$.
Niestety dany ciąg trójek jest sfałszowany -- nie istnieje ciąg $(x_i)$, który by go spełniał.
Twoim zadaniem jest znalezienie takiego $k$, że dla pierwszych $k$ danych trójek istniejej jeszcze spełniający je ciąg, a dla $k+1$ już nie.
Napisz procedurę przedzialy: int → (int * int * int) list → int, która dla danego $n$ oraz ciągu trójek oblicza takie $k$.

Informatyka MIMUW

Ćwiczenia 17: Imperatywne wskaźnikowe struktury danych