Informatyka MIMUW

Kombinacje liniowe, układy i zbiory liniowo niezależne, układy i zbiory generujące.

Niech $V$ będzie przestrzenią wektorową nad ciałem $\mathbb K$.

Kombinacją liniową wektorów $v_1,..., v_n\in V$ nazywamy wyrażenie

gdzie $\lambda _1,...,\lambda _n$ są skalarami z ciała $\mathbb K$. Wartością kombinacji liniowej (1.1) nazywamy wektor równy $\lambda _1v_1+...+\lambda _nv_n$. Skalary $\lambda _1,...,\lambda _n$ nazywamy współczynnikami kombinacji liniowej (1.1). Kombinację liniową nazywamy trywialną, jeśli wszystkie jej współczynniki są zerami. Kombinację liniową nazywamy zerową, jeśli jej wartość jest wektorem zerowym. Każda kombinacja liniowa trywialna jest zerowa. Oczywiście nie każda kombinacja zerowa jest trywialna. Na przykład, kombinacja liniowa $1\cdot v+(-1)\cdot v$ jest zerowa i nietrywialna.

W praktyce mówimy, że wektor $v$ jest kombinacją liniową pewnych wektorów mając na myśli to, że jest wartością tej kombinacji.

Wprowadzimy teraz fundamentalne dla naszego wykładu pojęcie liniowej niezależności.

Definicja 1.1 [Liniowa niezależność]

Mówimy, że ciąg wektorów $v_1,..., v_n$ przestrzeni wektorowej $V$ jest liniowo niezależny, jeśli spełniona jest następująca implikacja:

Jeżeli $\lambda _1v_1+...\lambda _nv_n =0$ dla pewnych skalarów $\lambda _1,...,\lambda _n$, to wszystkie te skalary muszą być zerami.

Innymi słowy, ciąg $v_1,...,v_n$ jest liniowo niezależny, jeżeli każda jego kombinacja liniowa, która jest zerowa, jest trywialna. Kolejność wektorów w ciągu $v_1,..., v_n$ jest w tej definicji nieistotna. Zamiast mówić o ciągach liniowo niezależnych, mówimy o układach liniowo niezależnych. Słowo układ zawiera najczęściej w sobie informację, że kolejność jego elementów jest nieistotna. Mówimy też o zbiorach liniowo niezależnych. Jasne jest, co to znaczy, że skończony zbiór jest liniowo niezależny. Różnica między zbiorem skończonym a układem jest taka, że w układzie mogą się pojawić wektory jednakowe.

Zbiór pusty uznajemy za liniowo niezależny.

Mówimy, że dowolny zbiór (niekoniecznie skończony) jest liniowo niezależny, jeśli każdy jego podzbiór skończony jest liniowo niezależny. Definicja taka nie prowadzi do żadnej sprzeczności z definicją liniowej niezależności w przypadku zbiorów skończonych, ponieważ zachodzi następujący lemat

Lemat 1.2 [Podukład]

Niech $v_1,...v_n$ będzie układem liniowo niezależnym. Wtedy każdy jego podukład jest też liniowo niezależny.

Dowód

Można założyć, że dany podukład składa się z wektorów $v_1,..., v_k$, gdzie $k<n$. Niech $\lambda _1v_1+...+\lambda _kv_k=0$. Wtedy

Korzystając teraz z liniowej niezależności wektorów $v_1,...,v_n$ dostajemy, że wszystkie współczynniki $\lambda _1,...,\lambda _k$ są zerami.

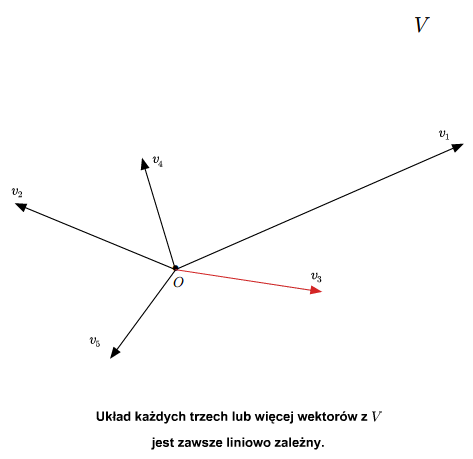
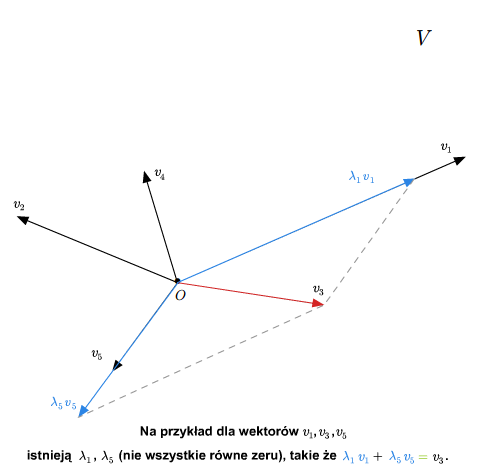
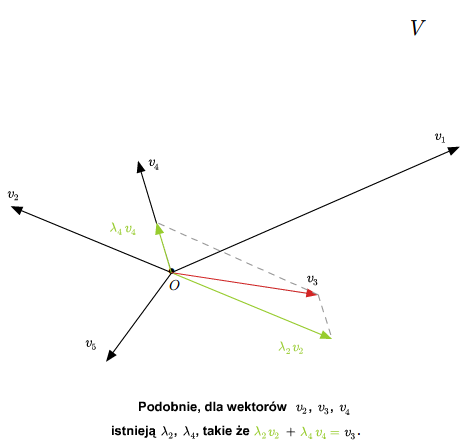
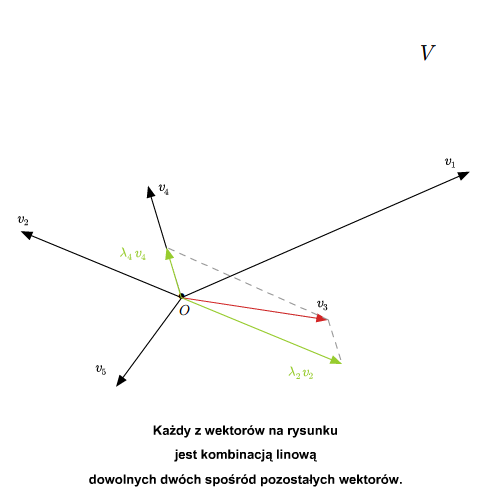
Mówimy, że wektory $v_1,...,v_n$ są liniowo zależne, jeśli nie są liniowo niezależne. A zatem, wektory $v_1,...,v_n$ są liniowo zależne, jeśli istnieją skalary $\lambda_1,...,\lambda _n\in \mathbb K$, nie wszystkie równe zeru takie, że $\lambda _1v_1+...+\lambda _nv_n =0$. Wtedy pewien wektor wśród $v_1,..., v_n$ mianowicie każdy, przy którym współczynnik w kombinacji $\lambda _1v_1+...+\lambda _nv_n=0$ jest niezerowy) da się przedstawić jako kombinacja liniowa pozostałych wektorów. Przypuśćmy, że $\lambda _1\ne 0$. Wtedy

Podkreślmy, że liniowa zależność wektorów $v_1,...,v_n$ nie oznacza, że każdy wektor wśród $v_1,...v_n$ jest kombinacją liniową pozostałych wektorów.

Al-3-2

AL-3-3

AL-3-4

AL-3-5

Każdy układ zawierający $0$ lub dwa jednakowe wektory jest liniowo zależny. Ponadto, układ dwóch wektorów $u,v\in V$ jest liniowo zależny wtedy i tylko wtedy, gdy wektory te są proporcjonalne, tzn. $v=\lambda u$ lub $u=\gamma v$ dla pewnych $\lambda, \gamma \in \mathbb K$. Sprawdzenie tych faktów pozostawiamy jako ćwiczenie.

Niech teraz $A$ będzie dowolnym podzbiorem przestrzeni $V$. Bierzemy rodzinę wszystkich podprzestrzeni wektorowych zawierających podzbiór $A$. Rodzina ta jest niepusta, bo cała przestrzeń $V$ należy do tej rodziny. A zatem przecięcie wszystkich zbiorów tej rodziny jest podprzestrzenią wektorową zawierającą $A$ (najmniejszą w sensie inkluzji). Oznaczmy tę podprzestrzeń symbolem $lin A$. Jeżeli $A$ jest zbiorem pustym, wtedy $lin A=\{0\}$. Jeżeli $W= lin A$, to mówimy, że $A$ generuje (rozpina) podprzestrzeń $W$. Oczywiście można też mówić o układzie $A$ i podprzestrzeni generowanej przez ten układ. Jest oczywiste, że jeśli $A\subset B$, to $lin A\subset lin B$. Jeśli $W$ jest podprzestrzenią wektorową, to $lin\, W =W$, a zatem dla dowolnego podzbioru $A$ mamy równość $lin ( lin A)= lin A$.

Twierdzenie 1.3 [Span]

Niech $A$ będzie niepustym podzbiorem przestrzeni wektorowej $V$. Wtedy

$lin A= \{ \lambda _1v_1+...+\lambda _kv_k\, |\ v_1,...,v_k\in A;\ \lambda _1,...,\lambda _k\in \mathbb K;\ k\in \mathbb N\}$      (1.2)

Podprzestrzeń generowana przez zbiór

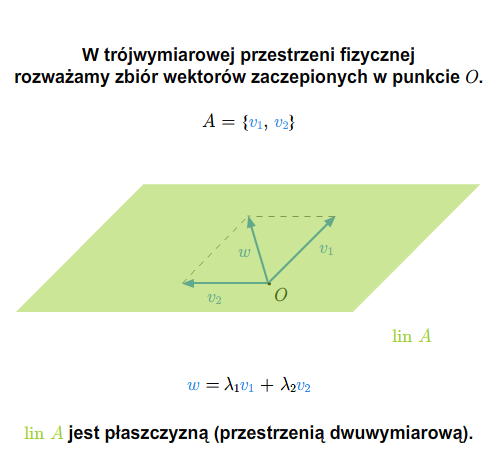
Dowód

Łatwo można sprawdzić, że zbiór znajdujący się po prawej stronie równości(1.2) jest podprzestrzenią wektorową zawierającą $A$. A zatem $A$ zawiera się w tym zbiorze. Odwrotnie, jest oczywiste, że każdy element tego zbioru (wartość kombinacji liniowej pewnych wektorów zbioru $A$) jest elementem podprzestrzeni wektorowej $lin A$.

W dalszym ciągu będziemy wykorzystywali następujące lematy.

Lemat 1.4

Niech $v_1,..., v_n$ będą wektorami liniowo niezależnymi i $w\notin lin \{v_1,...,v_n\}$. Wtedy wektory $v_1,...,v_n, w$ są liniowo niezależne.

Dowód

Niech

${\lambda _1}v_1+...+{\lambda _n}v_n +\lambda w=0.$

Gdyby $\lambda\ne 0$, to wektor $w$ byłby kombinacją liniową wektorów $v_1,...,v_n$, a zatem należałby do $lin \{v_1,...,v_n \}$, co byłoby sprzeczne z założeniem. A więc $\lambda =0$ i w konsekwencji mamy zerową kombinację liniową wektorów liniowo niezależnych $v _1,...,v_n$. A zatem wszystkie $\lambda _1$, ..., $\lambda _n$ są zerami.

Lemat 1.5

Niech wektor $w$ będzie kombinacją liniową wektorów $v_1,...v_n$, t.j. $w=\lambda _1v_1 +...+\lambda _n v_n$, dla pewnych skalarów $\lambda _1,...,\lambda _n$. Jeżeli $\lambda _1\ne 0$, to

$lin \{ v_1,...,v_n\} = lin \{w,v_2,...,v_n\}.$

Dowód

Ponieważ $w$ jest kombinacją liniową wektorów $v_1,...v_n$, więc $lin \{w,v_2,...,v_n\}\subset lin \{ v_1,...,v_n\}$.

Z drugiej strony, ponieważ $\lambda _1\ne 0$, więc

$v_1 ={1\over {\lambda _1}}w- {{\lambda _2}\over {\lambda _1}}v_2- ...-{{\lambda _n}\over {\lambda _1}}v_n.$

Zatem każda kombinacja liniowa wektorów $v_1,...v_n$ jest też kombinacją liniową wektorów $w,v_2,...,v_n$.

Twierdzenie 1.6

Niech $w_1,...,w_m$, $v_1,...v_n$ będą wektorami przestrzeni $V$. Jeżeli $w_1,...,w_m$ są liniowo niezależne oraz $w_1,..., w_m \in lin \{v_1,...,v_n\}$, to $m\le n$.

Dowód

Dla dowodu niewprost przypuśćmy, że $m>n$. Wektor $w_1$ jest kombinacja liniową wektorów $v_1,...,v_n$. Po ewentualnym spermutowaniu wektorów $v_1,...,v_n$, możemy przyjąć, że w tej kombinacji współczynnik przy $v_1$ jest różny od $0$. Z powyższego lematu mamy, że

$lin \{w_1,v_2,...,v_n\}= lin \{v_1,...,v_n\}.$

Ponieważ $w_2$ należy do tej przestrzeni, więc jest kombinacją liniową wektorów $w_1,v_2,...,v_n$. W kombinacji tej przynajmniej jeden ze współczynników przy wektorach $v_2,...,v_n$ musi być różny od zera. W przeciwnym bowiem przypadku, $w_1,w_2$ byłyby liniowo zależne. Po ewentualnym spermutowaniu wektorów $v_2,...,v_n$ możemy założyć, że współczynnik przy $v_2$ jest różny od zera. A zatem, korzystając z Lematu 1.5, dostajemy, że

$lin \{w_1,w_2,v_3,...,v_n \}= lin \{v_1,...,v_n\}.$

Postępujemy podobnie dalej, tzn. zastępujemy kolejne wektory $v_3,...$ wektorami $w_3,...$. Ponieważ założyliśmy, że $m>n$, więc dochodzimy do sytuacji, gdy $lin \{w_1,...w_n\}= lin\{v_1,...v_n\}$. Oznacza to sprzeczność, gdyż wektor $w_{n+1}$ musiałby być kombinacją liniową wektorów $w_1,...,w_n$.

Baza i wymiar przestrzeni

---

Wprowadzimy teraz kolejne fundamentalne dla naszego wykładu pojęcie.

Definicja 2.1 [Baza]

Mówimy, że podzbiór (lub układ, lub ciąg) $A$ przestrzeni wektorowej $V$ jest bazą tej przestrzeni, jeśli jest liniowo niezależny i generuje $V$.

Bazą przestrzeni zerowej jest zbiór pusty.

Twierdzenie 2.2 [Baza]

Załóżmy, że wektory $v_1,...,v_n$ generują przestrzeń wektorową $V$. Z wektorów $v_1,..., v_n$ można wybrać bazę przestrzeni $V$.

Dowód

Weźmy wszystkie podukłady układu $v_1,...,v_n$ i wśród tych, które są liniowo niezależne, wybierzmy maksymalny, czyli o maksymalnej długości. (Taki podukład nie musi być jedyny.) Możemy założyć, że $v_1,...,v_m$ jest takim podukładem. Twierdzimy, że jest to baza $V$. Gdyby bowiem nie była to baza, to któryś z pozostałych wektorów $v_{m+1},..., v_n$, powiedzmy $v_{m+1}$, nie byłby kombinacją liniową wektorów $v_1,...,v_m$. A zatem wektory $v_1,...,v_{m+1}$ byłyby liniowo niezależne, na podstawie Lematu 1.4. Oznacza to, że podukład $v_1,...,v_m$ nie byłby maksymalnym podukładem liniowo niezależnym.

Definicja 2.3 [Skończona wymiarowość]

Mówimy, że przestrzeń wektorowa jest skończenie wymiarowa, jeśli ma skończony układ generujący.}

Z powyższych twierdzeń wynika następujący wniosek

Twierdzenie 2.4

Przestrzeń skończenie wymiarowa $V$ ma bazę.

Wykażemy ponadto

Twierdzenie 2.5

W przestrzeni skończenie wymiarowej wszystkie bazy są równoliczne, czyli mają tyle samo elementów.

Dowód

Niech $B_1=\{e_1,..., e_n\}$ będzie skończoną bazą przestrzeni $V$, a zatem, skończonym zbiorem generującym $V$. Załóżmy, że $B_2$ jest inną bazą tej przestrzeni. Wtedy każdy skończony podzbiór $B_2$ jest liniowo niezależny. Z Twierdzenia 1.6 wynika, że każdy taki podzbiór ma co najwyżej $n$ elementów. Oznacza to, że zbiór $B_2$ jest skończony i ma co najwyżej $n$ elementów. Zamieńmy teraz rolami bazy $B_1$ i $B_2$. Potraktujmy $B_2$ jako zbiór generujący $V$, zaś $B_1$ jako zbiór liniowo niezależny. I znowu z Twierdzenia 1.6 wynika, że zbiór $B_1$ ma co najwyżej tyle elementów co zbiór $B_2$.

Na podstawie powyższego twierdzenia możemy podać następującą definicję wymiaru przestrzeni skończenie wymiarowej.

Definicja 2.6 [Wymiar]

Wymiarem przestrzeni skończenie wymiarowej nazywamy liczbę wektorów pewnej (lub, co na jedno wychodzi, każdej) bazy tej przestrzeni. Wymiar przestrzeni $V$ oznaczamy symbolem $\dim V$.

Kolejne twierdzenie jest natychmiastową konsekwencją powyższych rozważań.

Wniosek 2.7

Przestrzeń wektorowa jest skończenie wymiarowa wtedy i tylko wtedy, gdy ma bazę skończoną. Jeżeli $e_1,...,e_n$ jest bazą przestrzeni $V$, to każdy wektor $v$ przestrzeni $V$ da się w sposób jednoznaczny przedstawić jako kombinacja liniowa wektorów $e_1,...,e_n$.

Dowód

Sprawdźmy jednoznaczność w ostatniej tezie. Jeśli $e_1,...,e_n$ jest ustaloną bazą i $v=\lambda _1e_1+...\lambda_ne_n$ oraz $v=\lambda' _1e_1+...\lambda'_ne_n$, to $(\lambda_1 -\lambda' _1)e_1+...+(\lambda_n-\lambda'_n)e_n=0$. Z liniowej niezależności wektorów bazy dostajemy, że $\lambda _i=\lambda'_i$ dla każdego $i=1,...n$.

Jeżeli mamy bazę $e_1,...,e_n$ przestrzeni wektorowej $V$ i wektor $v=\lambda _1e_1+...+\lambda _ne_n$, to skalary $\lambda _1,...,\lambda _n$ nazywamy współrzędnymi wektora $v$ w bazie $e_1,..., e_n$.

Najważniejszym i najłatwiejszym przykładem bazy jest tak zwana baza kanoniczna przestrzeni $\mathbb K ^n$. Mianowicie, baza ta jest ciągiem

$(1,0,...,0 ), \ \ (0,1,0, ...,0),\ \ ...\ \ , (0,...,0, 1).$

Bardzo często kolejność wektorów bazy jest istotna. Aby to podkreślić, mówimy, że baza jest uporządkowana. Baza kanoniczna jest uporządkowana w naturalny sposób.

Twierdzenie 2.8

Niech $v_1,...,v_m$ będzie układem liniowo niezależnym w skończenie wymiarowej przestrzeni wektorowej $V$. Układ ten można uzupełnić do bazy, a zatem istnieje baza przestrzeni $V$ zawierająca dany układ liniowo niezależny.

Dowód

Niech $W_1 = lin \{ v_1,..., v_m\}$. Jeżeli $W_1\ne V$, to istnieje wektor $v_{n+1}$ w $V$, który nie należy do $W_1$. Wtedy, na podstawie Lematu 1.4, zbiór $v_1,...,v_n, v_{m+1}$ jest liniowo niezależny. Jeśli zbiór ten nie jest bazą $V$, postępujemy tak jak poprzednio. To znaczy, bierzemy wektor $v_{m+2}\notin lin \{v_1,...,v_n,v_{n+1}\}$ i dołączamy go do poprzednich wektorów. Postępując tak skończoną ilość razy otrzymujemy bazę przestrzeni $V$.

Z twierdzenia tego wynika natychmiast

Wniosek 2.9

Każda podprzestrzeń $W$ przestrzeni skończenie wymiarowej $V$ jest skończenie wymiarowa i jej wymiar jest nie większy od wymiaru przestrzeni $V$. Bazę $e_1,...,e_n$ przestrzeni $V$ można wybrać w ten sposób, że pierwsze jej wektory $e_1,..., e_m$ stanowią bazę podprzestrzeni $W$.

Dowód

Niech $e_1,...,e_m$ będzie bazą przestrzeni $W$. Baza ta jest zbiorem liniowo niezależnym w $V$, a zatem, na podstawie Twierdzenia 2.8, można ten zbiór uzupełnić do bazy całej przestrzeni $V$.

Zauważmy jeszcze, że jeśli $V$ jest przestrzenią skończenie wymiarową a $U$ jest jej podprzestrzenią taką, że $\dim U=\dim V$, to $V=U$. Istotnie, wybierzmy pewną, powiedzmy $n$-elementową, bazę przestrzeni $U$. Rozrzerzmy ją do bazy przestrzeni wektorowej $V$. Ale ta rozrzerzona baza też musi mieć $n$ elementów, a zatem wybrana baza przestrzeni $U$ jest też bazą przestrzeni $V$. To oczywiście implikuje, że $U=V$.

Jeżeli mamy zbiór (lub układ wektorów) $A$ przestrzeni wektorowej $V$ i podprzestrzeń $lin A$ jest skończenie wymiarowa, to rzędem $A$ nazywamy liczbę $\dim lin A$. Rząd $A$ oznaczać będziemy symbolem $rk A$.

Twierdzenie 2.10

Niech $U$, $W$ będą podprzestrzeniami przestrzeni skończenie wymiarowej przestrzeni wektorowej $V$. Zachodzi wtedy wzór

$\dim (U+W) =\dim U+\dim W - \dim (U\cap W).$

Dowód

Wiemy już, że przestrzenie $U$, $W$, $U\cap W$ są skończenie wymiarowe.

Niech $e_1,...,e_m$ będzie bazą $U\cap W$. Na podstawie Twierdzenia 2.8 wiemy, że układ ten można rozszerzyć do bazy przestrzeni $U$ oraz do bazy przestrzeni $W$.

Oznaczmy te bazy przez $e_1,...,e_m, e_{m+1} ...e_{n_1}$ oraz $e_1,..., e_m,e'_{m+1},..., e'_{n_2}$ odpowiednio. Twierdzimy, że zbiór

$e_1,...,e_m, e_{m+1},..., e_{n_1},e'_{m+1},..., e'_{n_2}$      (2.3)

jest bazą przestrzeni $U+W$.

Sprawdźmy najpierw generowanie. Niech $v\in U + W$. Wtedy $v=u+w$, gdzie $u\in U$ i $w\in W$. Istnieją skalary $\alpha _1,..., \alpha _{n_1}$ oraz $\beta _1,..., \beta _{n_2}$ takie, że

$u=\alpha _1 e_1+...+\alpha _{n_1} e_{n_1},$

$w =\beta _1 e_1+...+\beta _m e_m + \beta _{m+1}e'_{m+1}+...+\beta _{n_2} e'_{n_2}.$

Wobec tego

$v=(\alpha _1+\beta _1) e_1+...+ (\alpha _m +\beta _m)e_m + \alpha _{m+1}e_{m+1}+ ...+\alpha _{n_1} e_{n_1}$

$+\beta _{m+1}e'_{m+1}+...+\beta _{n_2} e'_{n_2}.$

Sprawdzimy teraz liniową niezależność układu (2.3). Niech

$0=\lambda _1 e_1+...+ \lambda _m e_m + \lambda _{m+1}e_{m+1}+ ...+\lambda _{n_1} e_{n_1} + \lambda ' _{m+1}e'_{m+1}+...+\lambda ' _{n_2} e'_{n_2}.$      (2.4)

Oznaczmy przez $w$ wektor $\lambda ' _{m+1}e'_{m+1}+...+\lambda '_{n_2} e'_{n_2}$, zaś przez $u$ wektor $\lambda _1 e_1+...+\lambda _m e_m + \lambda _{m+1}e_{m+1}+ ...+\lambda _{n_1}e_{n_1}$. Wtedy $u=-w$. Wektor $u$ należy do $U$, a wektor $w$ do $W$. A zatem obydwa te wektory należą do podprzestrzeni $U\cap W$. Oznacza to, że $w =\gamma _1e_1+... +\gamma _m e_m$ i w konsekwencji mamy

$\gamma _1e_1+... +\gamma _m e_m -(\lambda ' _{m+1}e'_{m+1}+...+\lambda ' _{n_2} e'_{n_2})=0.$

Z liniowej niezależności układu $e_1,...,e_m,e'_{m+1},..., e'_{n_2}$ dostajemy, że skalary $\lambda '_{m+1},..., \lambda '_{n_2}$ są równe zeru. Wracając teraz do równości (2.4) i korzystając z liniowej niezależności układu $e_1,..., e_{n_1}$ otrzymujemy, że $\lambda _1,...,\lambda _{n _1}$ są również równe zeru. Dowód został zakończony.

Wróćmy teraz do pojęcia sumy prostej zdefiniowanego w poprzednim wykładzie.

Na podstawie Twierdzenia 2.10 mamy

Wniosek 2.11

Jeśli $V$ jest skończenie wymiarowa i $V=U\oplus W$, to $\dim V=\dim U +\dim W$.

Mamy ponadto

Twierdzenie 2.12

Niech $V$ będzie skończenie wymiarową przestrzenią wektorową a $U$ jej podprzestrzenią. Istnieje wtedy dopełnienie algebraiczne do $U$.

Dowód

Niech $e_1,...e_m$ będzie bazą $U$. Rozszerzmy ten układ do do bazy przestrzeni $V$. Oznaczmy tę rozszerzoną bazę przez $e_1,...,e_m, e_{m+1},..., e_n.$ Oznaczmy przez $W$ przestrzeń rozpiętą na wektorach $e_{m+1},..., e_n$. Wtedy $V=U\oplus W$.

Zauważmy, że dopełnienie algebraiczne nie jest wyznaczone jednoznacznie.

Zakończymy ten wykład uwagami o przestrzeniach nieskończenie wymiarowych.

Przestrzeń $V$ nazywa się przestrzenią nieskończenie wymiarową, jeśli nie jest skończenie wymiarowa. Mamy następujący lemat

Lemat 2.13

Jeśli przestrzeń $V$ zawiera nieskończony zbiór wektorów liniowo niezależnych, to $V$ jest nieskończenie wymiarowa.

Dowód

Gdyby przestrzeń $V$ była skończenie wymiarowa, to na podstawie Twierdzenia 1.6, każdy zbiór liniowo niezależny tej przestrzeni byłby skończony.

Dowodzi się, co wykracza poza ramy tego wykładu, że w każdej przestrzeni wektorowej (również nieskończenie wymiarowej) istnieje baza i wszystkie bazy danej przestrzeni są równoliczne (czyli bijektywne).