Odwzorowania liniowe | Informatyka MIMUW

Definicja odwzorowania liniowego

Definicja 1.1 [Odwzorowanie liniowe]

Niech $V$ , $W$ będą przestrzeniami wektorowymi nad ciałem $\mathbb K$ i niech $f: V\longrightarrow W$ będzie odwzorowaniem. Mówimy, że $f$ jest liniowe, jeśli spełnione są następujące warunki

L 1) dla każdych wektorów $u,v\in Vf(u+v)=f(u)+f(v)$ ,

L 2) dla każdych $\lambda \in \mathbb K$ i $v\in Vf(\lambda v)=\lambda f(v)$ .

Własność pierwszą nazywamy addytywnością odwzorowania $f$ , drugą - jednorodnością $f$ .

Zespół warunków L 1) i L 2) można zastąpić jednym z następujących warunków L 3) lub L4).

L 3) Dla każdych $\lambda ,\mu \in \mathbb K$ i dla każdych $u,v\in V$ zachodzi równość $f(\lambda u+\mu v)=\lambda f(u) +\mu f(v)$ .

L 4) Dla każdych skalarów $\lambda _1,...,\lambda _k\in \mathbb K$ , wektorów $v_1,...,v_k\in V$ i każdego $k\in \mathbb N$ , zachodzi równość

$f(\lambda _1v_1+...+\lambda _kv_k) =\lambda _1f(v_1)+...+\lambda _kf(v_k).$

Dowód równoważności warunków L 3) i L 4) polega na zastosowaniu indukcji.

Zauważmy od razu, że $f(0)=f(0\cdot v)= 0\cdot f(v)$ , gdzie $v$ jest dowolnym wektorem przestrzeni $V$ . A zatem, dla odwzorowania liniowego zawsze mamy $f(0)=0$ .

Przykład 1.2

Odwzorowanie stale równe zeru jest liniowe. Odwzorowanie identycznościowe dowolnej przestrzeni wektorowej na siebie jest liniowe. Odwzorowanie to oznaczać będziemy przez $I$ .

Przykład 1.3

Weźmy przestrzeń $V$ wszystkich funkcji ciągłych na przedziale $(a,b)\subset \mathbb R$ o wartościach w $\mathbb R$ . Odwzorowanie

$V\ni f\longrightarrow \int f\in \mathbb R ^{(a,b)}$

jest odwzorowaniem liniowym.

Podobny przykład otrzymuje się dla całki oznaczonej.

Rozważmy jeszcze przestrzeń $U$ funkcji różniczkowalnych na przedziale $(a,b)\subset \mathbb R$ i odwzorowanie przyporządkowujące funkcji z $U$ jej pochodną. Odwzorowanie to jest liniowe.

Sprzężenie w

$\mathbb C$ nie jest liniowe

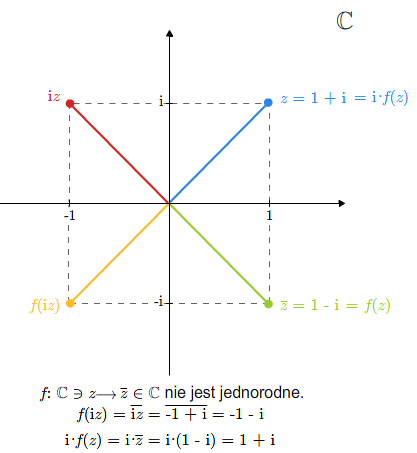
Przykład 1.4

Rozważmy odwzorowanie $f:\mathbb C\ni z \longrightarrow \overline z\in \mathbb C$ . Jeśli potraktujemy odwzorowanie $f$ jako odwzorowanie przestrzeni wektorowych nad ciałem $\mathbb C$ , to odwzorowanie to nie jest liniowe, bo nie jest jednorodne.

Jeśli jednak potraktujemy $\mathbb C$ jako przestrzeń wektorową nad ciałem $\mathbb R$ , to odwzorowanie $f$ jest liniowe. Mówimy, że $f$ jest $\mathbb R$ -liniowe, ale nie jest $\mathbb C$ -liniowe.

Własności odwzorowań liniowych. Obraz i jądro.

Omówimy teraz podstawowe własności odwzorowań liniowych.

Twierdzenie 2.1

Złożenie odwzorowań liniowych jest odwzorowaniem liniowym. Jeśli odwzorowanie liniowe jest bijekcją, to odwzorowanie odwrotne jest też liniowe.

Dowód

Tezy pierwszej dowodzi się bezpośrednim rachunkiem, co zostawiamy czytelnikowi. Dla sprawdzenia drugiej tezy ustalmy, że $f:V\longrightarrow W$ jest liniową bijekcją. Niech $w,w'\in W$ . Wtedy istnieją jedne jedyne wektory $v,v'\in V$ takie, że $w=f(v)$ i $w'=f(v')$ . Zatem $v=f^{-1}(w)$ i $v' =f^{-1}(w')$ . Niech $\lambda, \mu$ będą dowolnymi skalarami. Zachodzą równości

$f^{-1} (\lambda w+\mu w')= f^{-1} (\lambda f(v) +\mu f(v') ) = f^{-1}(f(\lambda v+\mu v'))$

$=\lambda v+\mu v'=\lambda f^{-1}(w)+\mu f^{-1} (w').$

Istotne cechy odwzorowań liniowych, często wykorzystywane w dalszej części wykładu, opisują następujące lematy

Lemat 2.2

Niech $A$ będzie zbiorem generującym przestrzeń $V$ i odwzorowania $f, h: V\longrightarrow W$ będą liniowe. Jeśli $f_{|A }=h_{|A}$ , to $f=h$ .

Dowód

Niech $v\in V$ będzie dowolnym wektorem. Istnieją wektory $v_1,...,v_n$ ze zbioru $A$ oraz skalary $\lambda _1,...,\lambda _n$ takie, że $v=\lambda _1v_1+...+\lambda _nv_n$ . Ponieważ obydwa odwzorowania $f$ i $h$ są liniowe, więc $f(v)=\lambda _1f(v_1)+...+\lambda _nf(v_n)= \lambda _1h(v_1)+...+\lambda _nh(v_n)=h(v)$ .

Lemat 2.3

Niech $B$ będzie bazą przestrzeni $V$ i $\tilde f: B\longrightarrow W$ będzie dowolnym odwzorowaniem.

Istnieje dokładnie jedno odwzorowanie liniowe $f: V\longrightarrow W$ takie, że $\tilde f =f_{| B}$

Dowód

Dla dowolnego $v$ istnieją wektory $e_1,..., e_n$ należące do bazy i skalary $\lambda _1,..., \lambda _n$ takie, że $v=\lambda _1e_1+...+\lambda _ne_n$ . Wybór wektorów z bazy i skalarów jest jednoznaczny. A zatem $f$ zadane formułą

$f(v)= \lambda _1\tilde f(e_1)+...+\lambda _n\tilde f(e_n)$ (2.1)

jest dobrze określone. Łatwo sprawdzić, że jest liniowe. Jest też oczywiste, że $f$ musi być zadane formułą (2.1). Stąd jedyność $f$ (lub z poprzedniego lematu).

Ostatni lemat mówi, że odwzorowanie liniowe może być zadane na bazie. Lemat dotyczy także przestrzeni nieskończenie wymiarowych.

Twierdzenie 2.4

Niech $f: V\longrightarrow W$ będzie odwzorowaniem liniowym. Jeżeli $U$ jest podprzestrzenią $V$ , to obraz podprzestrzeni $U$ przez odwzorowanie f, czyli $f(U)$ , jest podprzestrzenią $W$ . Jeżeli $U$ jest podprzestrzenią $W$ , to przeciwobraz podprzestrzeni $U$ przez odwzorowanie $f$ , czyli $f^{-1}(U)$ , jest podprzestrzenią $V$ .

Dowód

Jeżeli $w, z\in f(U)$ , to $w=f(v)$ i $z=f(u)$ dla pewnych $u, v\in U$ . Zatem $v+u\in U$ i $w+z=f(v)+f(u)=f(v+u)\in f(U)$ . Ponieważ $\lambda u\in U$ , więc $\lambda z= \lambda f(u)=f(\lambda u)\in f(U)$ dla dowolnego skalara $\lambda$ .

Niech $u,v\in f^{-1}(W)$ . Wtedy $f(u),f(v)\in W$ i, w konsekwencji, $f(u)+f(v)\in W$ . Zatem $f(u+v)=f(u)+f(v)\in W$ . Podobnie $f(\lambda u)=\lambda f(u)\in W$ dla dowolnego $\lambda$ .

Dla odwzorowania liniowego definiuje się dwie ważne podprzestrzenie - obraz i jądro odwzorowania liniowego.

Definicja 2.5 [Jądro odwzorowania]

Niech $f:V\longrightarrow W$ będzie odwzorowaniem liniowym. Jądrem odwzorowania $f$ nazywamy podprzestrzeń $f^{-1}(\{0\})$ . Jądro oznaczamy symbolem $\ker f$ . Obrazem $f$ nazywamy podprzestrzeń $f(V)$ przestrzeni $W$ . Przestrzeń tę oznaczamy $im f$ . Wymiar przestrzeni $im f$ nazywamy rzędem odwzorowania $f$ i oznaczamy $rk f$ .

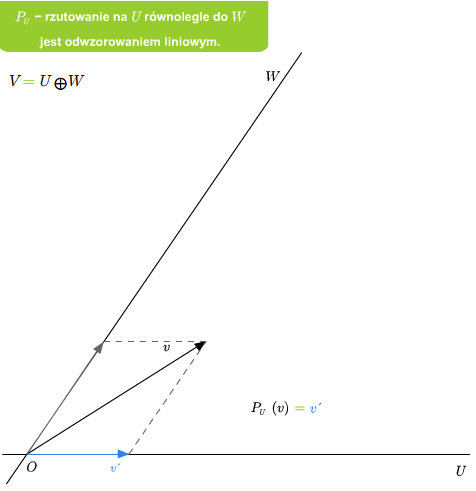
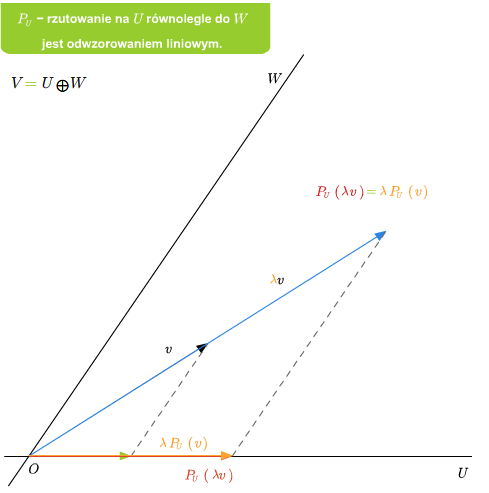
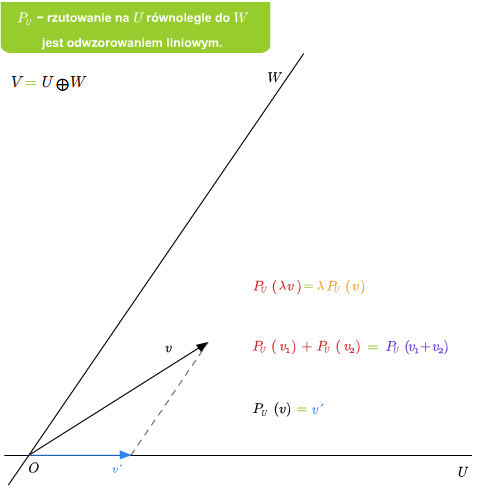
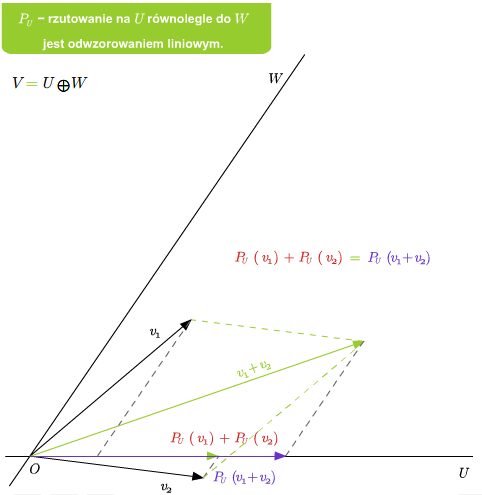
Rzutowanie równolegle do podprzestrzeni

Przykład 2.6

Jeśli dana jest suma prosta $V=U\oplus W$ , to rzutowanie $P_U$ na U równolegle do $W$ jest liniowe. Ponadto $\ker P_U=W$ oraz $im P_U=U$ .

Kolejny lemat wykorzystamy w dalszej części wykładu.

Lemat 2.7

Jeśli zbiór $A$ generuje przestrzeń $V$ i $f:V\longrightarrow W$ jest odwzorowaniem liniowym, to $f(A)$ generuje przestrzeń $im f$ .

Dowód

Oczywiście $f(A)\subset im f$ , a więc $lin f(A)\subset im f$ . Niech $w\in im f$ i niech $v\in V$ będzie takim wektorem, że $f(v)=w$ . Istnieją skalary $\lambda _1,...,\lambda _n\in$ oraz wektory $v_1,...,v_n\in A$ takie, że $v=\lambda _1v_1+...+\lambda _nv_n$ . Zatem $w= f(v)= \lambda _1 f(v_1)+...+\lambda _n f(v_n)\in lin f(A)$ .

Monomorfizmy. epimorfizmy, izomorfizmy

Definicja 3.1 [Monomorfizm]

Niech $f$ będzie odwzorowaniem liniowym Odwzorowanie $f$ nazywa się monomorfizmem, jeśli jest różnowartościowe. Odwzorowanie $f$ nazywa się epimorfizmem, jeśli jest surjekcją. Odwzorowanie, które jest jednocześnie monomorfizmem i epimorfizmem (czyli liniowa bijekcja) nazywa się izomorfizmem.

Podamy teraz łatwe, ale bardzo ważne, twierdzenie charakteryzujące monomorfizmy.

Twierdzenie 3.2

Niech $f:V\longrightarrow W$ będzie odwzorowaniem liniowym. Odwzorowanie to jest monomorfizmem wtedy i tylko wtedy, gdy $\ker f=\{0\}$ .

Dowód

Oczywiście $0\in\ker f$ . Niech $f$ będzie monomorfizmem. Jeśli $v\ne 0$ , to $f(v)\ne f(0)=0$ . Oznacza to, że jedynym elementem zbioru $\ker f$ jest wektor zerowy. Odwrotnie, jeśli $\ker f$ składa się tylko z elementu zerowego i $f(v)=f(u)$ , to $f(v-u)=f(v)-f(u)=0$ , a więc $u-v\in\ker f$ . Ponieważ $\ker f=\{0\}$ , więc $u=v$ . Zatem $f$ jest różnowartościowe.

Kolejne twierdzenie zawiera pewną charakteryzację monomorfizmów, epimorfizmów i izomorfizmów.

Twierdzenie 3.3

Niech $f: V\longrightarrow W$ będzie odwzorowaniem liniowym.

Jeżeli $f$ jest monomorfizmem, to $f$ przekształca każdy zbiór liniowo niezależny na zbiór liniowo niezależny.
Jeżeli $f$ przekształca injektywnie pewną bazę przestrzeni $V$ na zbiór liniowo niezależny, to $f$ jest monomorfizmem.
Jeżeli $f$ jest epimorfizmem, to $f$ przekształca każdy zbiór generujący $V$ na zbiór generujący przestrzeń $W$ .
Jeżeli $f$ przekształca pewien zbiór generujący $V$ na zbiór generujący $W$ , to $f$ jest epimorfizmem.
Jeżeli $f$ jest izomorfizmem, to przekształca każdą bazę przestrzeni $V$ na bazę przestrzeni $W$ .
Jeżeli $f$ przekształca injektywnie pewną bazę przestrzeni $V$ na bazę przestrzeni $W$ , to $f$ jest izomorfizmem.

Dowód

Rozważmy implikację 1.

Niech $B$ będzie zbiorem liniowo niezależnym w $V$ . Niech $w_1,...,w_n$ będą różnymi między sobą wektorami z $f(B)$ takimi, że $\lambda _1 w_1+...+\lambda _nw_n =0$ . Istnieją $v_1,...,v_n\in B$ (różne między sobą, bo $f$ jest injekcją) takie, że $w_1=f(v_1),...,w_n=f(v_n)$ . Mamy równości: $f(\lambda _1 v_1+...+\lambda _nv_n) =\lambda _1 f(v_1)+...+\lambda _nf(v_n)=0$ . Ponieważ $f$ jest monomorfizmem, więc $\lambda _1 v_1+...+\lambda _nv_n =0$ . Wobec tego, ponieważ $v_1,...,v_n$ są liniowo niezależne, wszystkie $\lambda _i$ , dla $i=1,...,n$ , są równe zeru.

Dla dowodu drugiej implikacji, załóżmy, że $B$ jest bazą przestrzeni $V$ , przekształconą injektywnie na zbiór liniowo niezależny. Niech $f(v)=0$ . Istnieją skalary $\lambda _1,...,\lambda _n\in \mathbb K$ oraz wektory $v_1,...,v_n\in B$ takie, że $v=\lambda _1v_1+...+\lambda _nv_n$ . Mamy więc równość: $0=\lambda _1f(v_1)+...+\lambda _n(v_n)$ . Ponieważ $f$ jest injekcją na bazie, więc wektory $f(v_1),...,f(v_n)$ są różne między sobą. A zatem $f(v_1),...,f(v_n)$ jest skończonym podzbiorem $f(B)$ . Jest liniowo niezależny, a więc wszystkie skalary $\lambda _1$ ,..., $\lambda _n$ są równe $0$ i, w konsekwencji, $v=0$ .

Dowód pozostałych implikacji zostawiamy czytelnikowi.

Założenie w implikacji 2. w przypadku przestrzeni skończenie wymiarowych można sformułować tak:

Dla pewnej bazy $e_1,...,e_n$ przestrzeni $V$ układ $f(e_1),...,f(e_n)$ jest liniowo niezależny.

Podobnie formułuje się założenie w implikacji 6.

Z powyższego twierdzenia, a także z dobrze już znanych faktów, że w skończenie wymiarowej przestrzeni każdy układ liniowo niezależny można uzupełnić do bazy i z każdego układu generatorów można wybrać bazę, dostajemy natychmiast

Wniosek 3.4

Niech $V,W$ będą przestrzeniami skończenie wymiarowymi tego samego wymiaru. Niech $f:V\longrightarrow W$ będzie odwzorowaniem liniowym. Następujące warunki są równoważne

f jest monomorfizmem.
f jest epimorfizmem.
f jest izomorfizmem.

Z twierdzenia (3.3) wynika także

Wniosek 3.5

Jeżeli $f:V\longrightarrow W$ jest izomorfizmem liniowym i przestrzeń $V$ jest skończenie wymiarowa, to $W$ jest też skończenie wymiarowa oraz $\dim V=\dim W$ .

Rząd odwzorowania liniowego

Kolejne twierdzenie opisuje ważny związek między wymiarami jądra i obrazu danego odwzorowania liniowego.

Twierdzenie 4.1

Niech $f:V\longrightarrow W$ będzie odwzorowaniem liniowym. Jeżeli $V$ jest skończenie wymiarowa, to

$rk f + \dim\ker f =\dim V.$

Dowód

Jeżeli $\ker f=V$ lub $\ker f=\{0\}$ , twierdzenie jest trywialne. Załóżmy, że $\ker f\ne V$ i $\ker f\ne\{0\}$ . Niech $e_1,..., e_k$ będzie bazą $\ker f$ . Rozszerzmy tę bazę do bazy całej przestrzeni $V$ . Niech $e_1,...,e_k,e_{k+1},..., e_{n}$ będzie bazą rozszerzoną. Twierdzimy, że wektory $f(e_{k+1}),..., f(e_{n})$ stanowią bazę przestrzeni $im f$ .

Sprawdźmy najpierw, że wektory te generują przestrzeń $im f$ . Jeśli $w\in im f$ , to istnieje $v\in V$ taki, że $f(v)=w$ . Wektor $v$ da się przedstawić jako kombinacja liniowa wektorów bazy $e_1,..., e_n$ , tzn. $v=\lambda _1e_1 +...+\lambda _ne_n$ . Zatem

$w=f(v) =\lambda _1\cdot 0+...+\lambda _k\cdot 0+ \lambda _{k+1}f(e_{k+1})+...+ \lambda _{n}f(e_{n}).$

Aby sprawdzić liniową niezależność tych wektorów, załóżmy, że

$\lambda _{k+1}f(e_{k+1})+...+ \lambda_{n}f(e_{n})=0$

dla pewnych skalarów $\lambda _{k+1},...\lambda _n$ . Wtedy $f(\lambda _{k+1}e_{k+1}+...+ \lambda _{n}e_{n})=0$ , czyli $\lambda _{k+1}e_{k+1}+...+ \lambda _{n}e_{n} \in \ker f$ . Wobec tego istnieją skalary $\lambda _1,...,\lambda _k$ takie, że

$\lambda _{k+1}e_{k+1}+...+ \lambda _{n}e_{n} = \lambda _1e_1+...+ \lambda _{k}e_{k} .$

Ponieważ układ wektorów $e_1,...,e_k, e_{k+1},..., e_n$ jest liniowo niezależny, wszystkie skalary w powyższej równości, w szczególności skalary $\lambda _{k+1},..., \lambda _n$ , są równe $0$ .

Z Twierdzenia 2.7 otrzymujemy natychmiast

Wniosek 4.2

Niech $V$ i $W$ będą skończenie wymiarowe. Dla odwzorowania liniowego $f:V\longrightarrow W$ jego rząd spełnia nierówność

$rk f\le min\{\dim V, \dim W\}.$

Przestrzeń dualna

Przypomnijmy sobie Przykład 7. z Wykładu 2. Wiemy z niego, że ogół odwzorowań prowadzących z niepustego zbioru $V$ do przestrzeni wektorowej $W$ jest przestrzenią wektorową z działaniami wprowadzonymi w Przykładzie 7. Przypomnijmy, że

$(f+h)(v)=f(v)+h(v),$

$(\lambda f)(v)=\lambda (f(v))$

dla $f,h\in W^V$ , $v\in V$ i $\lambda \in\mathbb K$ . Niech $V,W$ będą, jak w całym tym wykładzie, przestrzeniami wektorowymi nad jednym ciałem $\mathbb K$ i $f, h:V\longrightarrow W$ - odwzorowaniami liniowymi. Łatwo widać, że suma tych odwzorowań, a także iloczyn odwzorowania liniowego przez skalar są odwzorowaniami liniowymi. Zatem ogół odwzorowań liniowych z przestrzeni $V$ do $W$ stanowi podprzestrzeń wektorową przestrzeni $W^V$ .

Rozważmy sytuację szczególną. Za $W$ weźmy ciało $\mathbb K$ . Przestrzeń odwzorowań liniowych prowadzących z $V$ do $\mathbb K$ oznaczmy przez $V^*$ . Przestrzeń tę nazywamy przestrzenią dualną do $V$ . A zatem

$V^*=\{\alpha :V\longrightarrow \mathbb K \ |\ \alpha \ \ {\rm liniowe}\}.$

Załóżmy teraz, że przestrzeń $V$ jest skończenie wymiarowa i ma wymiar $n$ . Niech $e_1,..., e_n$ będzie bazą tej przestrzeni. Zdefiniujemy ciąg $e^*_1,..., e^*_n$ elementów przestrzeni $V^*$ następująco. Pamiętając o tym, że odwzorowanie liniowe możemy zadać na bazie, określamy

$e^*_i(e_j)=\delta _{ij},$ (5.2)

gdzie $\delta _{ij}$ jest tzw. deltą Kroneckera. Symbol ten zdefiniowany jest następująco: $\delta _{ij}=0$ dla $i\ne j$ oraz $\delta _{ij}=1$ dla $i=j$ .

Udowodnimy teraz

Twierdzenie 5.1

Ciąg $e^*_1,..., e^*_n$ jest bazą przestrzeni $V^*$ .

Dowód

Układ $e^*_1,..., e^*_n$ jest liniowo niezależny. Istotnie, niech

$\lambda _1e^*_1+...+\lambda _ne ^*_n=0.$ (5.3)

Zero występujące z prawej strony tej równości oznacza odwzorowanie tożsamościowo równe zeru. Oznaczmy przez $\alpha$ odwzorowanie określone przez lewą stroną równości (5.3). Dla każdego $v\in V$ mamy $\alpha (v)=0$ . W szczególności dla każdego wektora $e_i$ bazy $e_1,...,e_n$ mamy $\alpha (e_i)=0$ . Wstawiając do obu stron równości (5.3) kolejne wektory bazy $e_1,..., e_n$ stwierdzamy, że $\lambda _1$ ,..., $\lambda _n$ są równe zeru.

Aby stwierdzić że $e^*_1,..., e^*_n$ stanowię zbiór generatorów przestrzeni $V^*$ wystarczy sprawdzić, że dla każdego $\alpha \in V^*$ mamy

$\alpha =\alpha (e_1)e^*_1+...+\alpha (e_n)e^*_n.$ (5.4)

Dla sprawdzenia tej równości, wystarczy porównać wartości odwzorowań liniowych znajdujących się po obydwu jej stronach na kolejnych wektorach bazy $e_1,...,e_n$ .

Formuła (5.4) jest sama w sobie ważna i bardzo pożyteczna.

Zauważmy jeszcze, że jeśli $f:V\longrightarrow W$ jest liniowe, to

definiując odwzorowanie

$f^*: W^* \longrightarrow V^*$

formułą

$f^* (\alpha) =\alpha\circ f,$

otrzymujemy odwzorowanie liniowe. Sprawdzenie zostawiamy czytelnikowi. Odwzorowanie to nazywamy odwzorowaniem dualnym (lub transponowanym) do $f$ .

Korzystając bezpośrednio z definicji odwzorowania dualnego, łatwo sprawdzić następujący fakt

Twierdzenie 5.2

Niech $f: V \longrightarrow W, h: W \longrightarrow Z$ będą odwzorowaniami liniowymi. Zachodzi równość odwzorowań

$(h \circ f)^* = f^* \circ h^* .$