Endomorfizmy. Twierdzenie Jordana

Wyznacznik, ślad, wartość własna, wielomian charakterystyczny endomorfizmu i macierzy

W wykładzie tym zakładamy, że wszystkie przestrzenie są skończenie wymiarowe nad ciałem \(\mathbb K\) o charakterystyce równej \(0\).

Mówimy, że macierze kwadratowe \(A, B\in M(n,n;\mathbb K)\) są podobne, jeśli istnieje taka macierz nieosobliwa \(P\), dla której \(B=P^{-1}AP\). Macierze podobne mają ten sam wyznacznik, bo

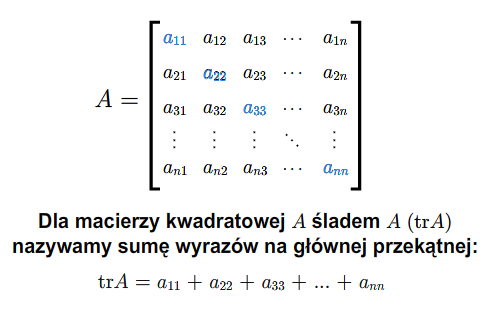
\(\det B =\det P^{-1}\det A\det P= {1\over{\det P}}\, \det A\, \det P=\det A.\)

Ślad macierzy

Zdefiniujemy teraz ślad macierzy. Tak jak wyznacznik, ślad macierzy definiuje się tylko dla macierzy kwadratowych. Dla macierzy \(A=[a_{ij}]\in M(n,n;\mathbb K)\) definiujemy jej ślad \(tr A\) jako sumę jej wyrazów leżących na głównej przekątnej, to znaczy

\(\displaystyle tr A=\sum _{i=1}^n a_{ii}.\)

Odwzorowanie

\(M(n,n;\mathbb K )\ni A\longrightarrow tr A \in \mathbb K\)

jest liniowe.

Pamiętamy, że mnożenie macierzy jest na ogół nieprzemienne. Mamy natomiast następujące twierdzenie

Twierdzenie 1.1

Dla dowolnych macierzy \(A,B\in M(n,n;\mathbb K )\) zachodzi równość

\( tr (AB)= tr (BA).\)

Dowód

Niech \(A=[a_{ij}]\), \(B=[b_{ij}]\). Oznaczmy przez \(C=[c_{ij}]\) macierz \(AB\) i przez \(D=[d_{ij}]\) macierz \(BA\). Mamy następujące równości

\(\displaystyle tr (AB)=\sum _{i=1}^n c_{ii}=\sum _{i=1}^n \sum _{k=1}^n a_{ik}b_{ki}= \sum _{k=1}^n\sum _{i=1}^m b_{ki}a_{ik} =\sum _{k=1}^n d_{kk}\)\(= tr (BA).\)

Z twierdzenia tego wynika, że macierze podobne mają taki sam ślad. Istotnie, \( tr (P^{-1}AP)= tr (P^{-1}(AP))= tr ((AP)P^{-1})= tr (A(PP^{-1}))= tr A\).

Niech \(f:V\longrightarrow V\) będzie endomorfizmem. Niech \(e_1,..., e_n\); \(e'_1,...,e'_n\) będą bazami przestrzeni \(V\). Jeśli \(A\) jest macierzą \(f\) przy bazie \(e_1,..., e_n\) zaś \(B\) jest macierzą \(f\) przy bazie \(e'_1,..., e'_n\), to \(B=P^{-1}AP\), gdzie \(P\) jest macierzą przejścia od bazy \(e_1,...,e_n\) do bazy \(e'_1,...,e'_n\). A zatem \(\det B=\det A\). Oznacza to, że niżej wprowadzona definicja ma sens, tzn. nie zależy od wyboru bazy \(e_1,...,e_n\).

Definicja 1.2

Wyznacznikiem endomorfizmu \(f:V\longrightarrow V\) nazywamy wyznacznik dowolnej macierzy tego endomorfizmu.

Podobnie definiuje się ślad endomorfizmu. Mianowicie, mając endomorfizm \(f\) bierzemy dowolną jego macierz \(A\) (tzn. macierz przy dowolnej bazie) i definiujemy \( tr f\) jako \( tr A\). Definicja nie zależy od wyboru bazy, bo macierze podobne mają ten sam ślad.

Wprowadzimy teraz kolejne definicje.

Definicja 1.3

Mówimy, że skalar \(\lambda\) jest wartością własną endomorfizmu \(f:V\longrightarrow V\), jeśli istnieje niezerowy wektor \(v\in V\) taki, że \(f(v)=\lambda v\). Każdy taki wektor \(v\) nazywamy wektorem własnym odpowiadającym wartości własnej \(\lambda\).

Definiuje się też wartości własne i wektory własne macierzy

Definicja 1.4

Mówimy, że skalar \(\lambda\) jest wartością własną macierzy \(A\in M(n,n;\mathbb K )\), jeśli istnieje niezerowy wektor \(v\in \mathbb K^n\) taki, że \(Av=\lambda v\). Każdy taki wektor \(v\) nazywamy wektorem własnym odpowiadającym wartości własnej \(\lambda\).

W powyższej równości \(Av=\lambda v\) wektor \(v\) jest traktowany jako \(1\)-kolumnowa macierz.

Istotną cechę wektorów i wartości własnych opisuje następujące twierdzenie

Twierdzenie 1.5

Jeżeli \(\lambda _1,...,\lambda _k\) są różnymi między sobą wartościami własnymi endomorfizmu \(f\) i \(v_1,...,v_k\) są wektorami własnymi odpowiadającymi tym wartościom własnym, to wektory \(v_1,...,v_k\) są liniowo niezależne.

Dowód

Dowód jest indukcyjny ze względu na \(k\). Dla \(k=1\) twierdzenie jest oczywiste. Załóżmy, że jest prawdziwe dla liczb mniejszych od pewnego \(k\).

Przypuśćmy, że wektory \(v_1,...,v_k\) spełniają założenia twierdzenia i wektory te są liniowo zależne. Możemy założyć, że \(v_k\) jest kombinacją liniową wektorów \(v_1,...,v_{k-1}\). Niech

\(v_k=\mu _1v_1+...+\mu _{k-1}v_{k-1},\)

Nie wszystkie \(\mu _1,...,\mu _{k-1}\) są równe zeru. Możemy przyjąć, że \(\mu _1\ne 0\). Obłóżmy powyższą równość przez \(f\). Wtedy

\(\lambda _k v_k=\mu _1\lambda _1v_1+...+\mu _{k-1}\lambda _{k-1} v_{k-1}.\)

Z drugiej strony

\(\lambda _kv_k=\lambda _k \mu _1 v_1+...+\lambda _k \mu _{k-1} v_{k-1}.\)

Zatem

\(0= \mu_1(\lambda _k-\lambda _1)v_1+...+\mu _{k-1}(\lambda _k-\lambda _{k-1})v_{k-1}.\)

Ponieważ \(v_1,...,v_l\) są liniowo niezależne i \(\mu _1\ne 0\), więc \(\lambda _k=\lambda _1\). Jest to sprzeczne z założeniem, że \(\lambda _1,..., \lambda _k\) są różne miedzy sobą.

Mamy następujące twierdzenie charakteryzujące wartości własne.

Twierdzenie 1.6

Skalar \(\lambda\) jest wartością własną endomorfizmu \(f\) wtedy i tylko wtedy, gdy

\(\det (f-\lambda I)=0,\)

gdzie \( I\) jest odwzorowaniem identycznościowym przestrzeni \(V\).

Dowód

Jeżeli \(\lambda\) jest wartością własną \(f\) i \(v\) jest wektorem własnym odpowiadającym wartości własnej \(\lambda\), to \((f-\lambda I)(v)=0\), czyli odwzorowanie \(f-\lambda I\) nie jest monomorfizmem. A zatem \(\det (f-\lambda I)=0\). Odwrotnie, jeśli \(\det (f-\lambda I)=0\), to \(f-\lambda I\) nie jest monomorfizmem, a zatem istnieje niezerowy wektor \(v\) taki, że \((f-\lambda I)(v)=0\). Oznacza to, że \(\lambda\) jest wartością własną \(f\) a \(v\) jest wektorem własnym odpowiadającym tej wartości własnej.

Wybierzmy bazę przestrzeni \(V\). Niech \(A\) będzie macierzą \(f\) przy tej bazie. Wtedy, dla każdego \(t\in \mathbb K\) mamy \(\det (f-t I) = \det (A-t I)\).

Jest jasne, jeśli skorzystamy na przykład ze wzoru na wyznacznik macierzy \(A=[a_{ij}]\) z Wykładu VII, tzn. ze wzoru

\(\displaystyle \det A= \sum _{\rho \in \S _n} sgn\ \rho \ a_{\rho (1)1}\cdot\cdot\cdot a_{\rho (n)n},\) (1.1)

że \(\det (f-t I)=\det (A-t I )\), traktowany jako funkcja argumentu \(t\) jest wielomianem stopnia \(n\). Wielomian ten nazywamy wielomianem charakterystycznym endomorfizmu \(f\). Oznaczmy go przez \(W_f\). W wielomianie tym współczynnik przy \(t^n\) jest równy \((-1)^n\), wyraz wolny jest równy \(\det A =\det f\), zaś współczynnik przy \(t^{n-1}\) jest równy \((1)^{n-1} tr A= tr f\). Istotnie, wstawiając za \(t\) wartość \(0\) dostajemy wyraz wolny wielomianu \(W_f\), czyli wyraz wolny jest równy \(\det f\). Wielomian \(W_f\) możemy zapisać jako

\(W_f(t)= (a_{11}-t)\cdot\cdot\cdot (a_{nn}-t) + W(t),\)

gdzie \(W(t)\) jest wielomianem stopnia mniejszego lub równego \(n-1\). Widać stąd, że współczynnik przy \(t^n\) jest równy \((-1)^n\). Zauważmy jednak, że wielomian \(W(t)\) jest stopnia silnie mniejszego od \(n-1\). Istotnie, ciągle mając na uwadze wzór (1.1), widzimy, że składniki zawierające \(t^{n-1}\) mogą powstać tylko przy pomnożeniu \(n-1\) wyrazów macierzy \(A-t I\) leżących na głównej przekątnej. Ale permutacja \(n\)-elementowego zbioru, która jest identycznością na \(n-1\) elementach jest identycznością na całym zbiorze. Oznacza to, że składniki wielomianu \(W_f(t)\) zawierające \(t^{n-1}\) powstają tylko z iloczynu \((a_{11}-t)\cdot\cdot\cdot (a_{nn}-t)\). Teraz łatwo widać, że współczynnik przy \(t^{n-1}\) jest równy \((-1)^{n-1} tr A\).

Podprzestrzenie niezmiennicze. Baza i macierz Jordana.

Niech \(U\) będzie podprzestrzenią przestrzeni \(V\). Mówimy, że podprzestrzeń ta jest \(f\)-niezmiennicza (dokładniej mówiąc, niezmiennicza ze względu na \(f\)), jeśli \(f(U)\subset U\). Jeśli \(U\) jest podprzestrzenią \(f\)-niezmienniczą, to po zawężeniu \(f\) do \(U\) dostajemy endomorfizm przestrzeni \(U\). Oznaczmy go przez \(\tilde f\). Endomorfizm ten ma swój wielomian charakterystyczny \(W_{\tilde f}\). Zachodzi następujący lemat.

Lemat 2.1

Jeżeli \(U\) jest podprzestrzenią \(f\)-niezmienniczą, to wielomian charakterystyczny \(W_{\tilde f}\) dzieli wielomian charakterystyczny \(W_f\).

Dowód

Niech \(e_1,...,e_k\) będzie bazą przestrzeni \(U\). Rozszerzamy ją do bazy \(e_1,...,e_k, e_{k+1},...,e_n\) przestrzeni \(V\). Macierz \(A\) endomorfizmu \(f\) w tej bazie ma postać blokową

\(A=\left [\begin{array} {l} \ B \ D \\ \ 0 \ C \end{array} \right ]\)

gdzie \(B\) jest macierzą \(\tilde f\) w bazie \(e_1,...,e_k\). Mamy wtedy (na podstawie Twierdzenia 2.6 z Wykładu VII)

\(W_f(t)= \det (A-t I) = \det (B- t I) \det (C-t I) =W_{\tilde f}\ \det (C-t I).\)

Macierzą Jordana nazywa się macierz postaci

\(\left [\begin{array} {lccccr} \ A_1 & 0 & 0 &...& 0\\ \ 0 &A_2&0 &...&0\\ \ & & & & \\ \ . & .& . & . & 0\\ \ . & . & . & .& 0\\ \ . & .& . & .& 0\\ \ & & & & \\ \ 0& 0& 0& 0& A_l, \end{array} \right ],\) (2.2)

gdzie \(A_1\), ..., \(A_l\) są macierzami kwadratowymi postaci

\(\left [\begin{array} {lcccccr} \ \lambda _i &1& & & & 0\\ \ 0& \lambda _i& 1& & & 0\\ \ .&. & .& .& .& .\\ \ 0 & & & \lambda _i & 1 & 0\\ \ 0 & & & &\lambda _i & 1\\ \ 0 & & & & &\lambda _i \end{array} \right ]\) (2.3)

dla \(i=1,...l\). Macierze \(A_1,..., A_l\) nazywamy klatkami Jordana. Jeżeli macierz \(A_i\) jest jedna klatką Jordana (2.3) o wymiarach \(n_i\) na \(n_i\), to \((A_i-\lambda _i I )^{n_i}=0\). Oczywiście \(\lambda _i\) jest wartością własną macierzy \(A_i\).

Zwróćmy uwagę na to, że klatki mogą też być wymiaru \(1\times 1\).

Każda klatka odpowiada pewnej wartości własnej macierzy \(A\). Dla danej wartości własnej odpowiadające jej klatki mogą mieć różne wymiary. Klatek w danym wymiarze też może być dowolna ilość.

Przypuśćmy, że dla danego endomorfizmu \(f\) istnieje taka baza \(e_1,...,e_n\), przy której macierz tego endomorfizmu jest macierzą Jordana. Poukładajmy klatki tej macierzy tak, aby na początku (tzn. począwszy od lewego górnego rogu macierzy) były klatki odpowiadające wartości własnej \(0\) - najpierw wymiaru 1\(\times\)1, potem wymiaru 2\(\times\)2, potem 3\(\times\)3, etc. Po klatkach odpowiadających wartości własnej \(0\), umieszczamy klatki odpowiadające pozostałym wartościom własnym. Dla każdej wartości własnej układamy klatki od najmniejszych do największych. Takie ukladanie klatek odpowiada permutowaniu bazy \(e_1,..., e_n\). Macierz po takim układaniu jest ciągle macierzą Jordana endomorfizmu \(f\), a spermutowana baza jest bazą Jordana dla \(f\). Bazę tę oznaczmy przez \(\mathcal B\).

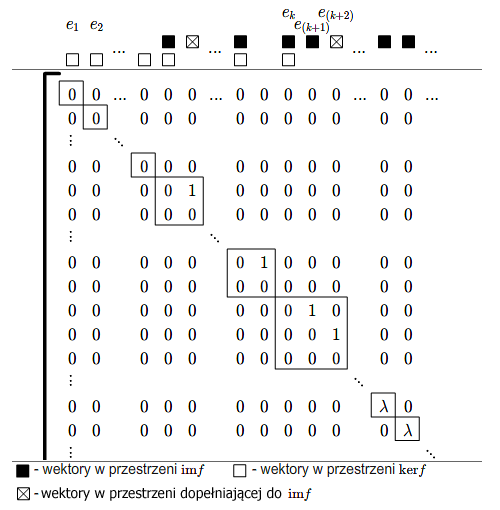
Obserwując macierz \(\mathcal B\) łatwo odczytać pewne cechy odwzorowania \(f\).

Dla ustalonej klatki mamy pewien ciąg wektorów bazy Jordana odpowiadający tej klatce. Ciąg taki zaczyna się od wektora własnego. Każdy wektor własny z bazy \(\mathcal B\) odpowiadający jakiejś wartości własnej rozpoczyna pewien ciąg wektorów (może być 1-wyrazowy) odpowiadający jednej klatce macierzy Jordana.

Z bazy Jordana \(\mathcal B\) można wybrać bazę podprzestrzeni \(\ker f\). Wektory tej bazy to wektory odpowiadające wszystkim klatkom 1\(\times\)1 dla wartości własnej \(0\) oraz pierwsze wektory (oczywiście ciągle z bazy \(\mathcal B\)) odpowiadające wszystkim kolejnym klatkom Jordana dla wartości własnej \(0\).

Z bazy \(\mathcal B\) można wybrać bazę podprzestrzeni \( im f\). W szczególności wszystkie wektory bazy \(\mathcal B\), które odpowiadają klatkom dla niezerowych wartości własnych stanowią część takiej bazy.

Ostatnie wektory ciągów odpowiadających poszczególnym klatkom Jordana i wartości własnej \(0\) rozpinają podprzestrzeń dopełniajacą do \( im f\). Bierzemy tu pod uwagę wszystkie klatki Jordana odpowiadające wartości własnej \(0\).

Macierz Jordana

Udowodnimy teraz twierdzenie Jordana.

Twierdzenie 2.2 [Jordana]

Niech \(f: V\longrightarrow V\) będzie endomorfizmem, dla którego wielomian charakterystyczny rozkłada się na iloczyn czynników stopnia 1. Istnieje baza Jordana dla \(f\).

Dowód

Dowód jest indukcyjny ze względu na wymiar \(n\) przestrzeni \(V\). Jeśli \(n=1\), to twierdzenie jest trywialne. Załóżmy, że twierdzenie jest prawdziwe dla przestrzeni wymiaru mniejszego od \(n\).

Załóżmy najpierw, że \(f\) nie jest monomorfizmem, czyli \(\dim im f<n\). Podprzestrzeń \( im f\) jest \(f\)-niezmiennicza. Niech \(\tilde f: im f \longrightarrow im f\) będzie zawężeniem \(f\) do \( im f\). Wielomian charakterystyczny dla \(\tilde f\) dzieli wielomian charakterystyczny dla \(f\). Zatem rozkłada się na iloczyn czynników stopnia 1. Możemy zastosować założenie indukcyjne dla edomorfizmu \(\tilde f\) przestrzeni \(f\). Niech \(\dim im f =m\) i \(w_1,..., w_m\) będzie bazą Jordana dla \(\tilde f\). Jeżeli \( im f\oplus \ker f=V\), to do bazy \(w_1,...,w_m\)dopisujemy dowolną bazę podprzestrzeni \(\ker f\) i mamy bazę Jordana dla \(f\).

Załóżmy teraz, że \( im f\cap \ker f\ne \{0\}\). Oczywiście \(\ker\tilde f=\ker f\cap im f\). Z bazy Jordana \(w_1,...,w_m\) wybieramy bazę przestrzeni \(\ker\tilde f\). Niech będzie to ciąg \(w_{i_1},...,w_{i_k}\). Wszystkie te wektory są wektorami własnymi \(\tilde f\) odpowiadającymi wartości własnej \(0\). Każdy z nich rozpoczyna pewien ciąg wektorów odpowiadający jednej klatce Jordana endomorfizmu \(\tilde f\). Oznaczmy przez \(\tilde w_{1},...,\tilde w_{k}\) ostatnie wektory tych ciągów. Ponieważ wektory te należą do \( im f\), więc istnieją wektory \(v_1,...,v_k\in V\) takie, że

\(f(v_1)=\tilde w_{1},...,f(v_k)=\tilde w_{k}\)

Bierzemy uzupełnienie \(u_1,..., u_{n-m-k}\) ciągu \(w_{i_1},...,w_{i_k}\) do bazy przestrzeni \(\ker f\).

Twierdzimy, że ciąg

\(w_1,...,w_m, v_1,...,v_k, u_1,...,u_{n-m-k}\) (2.4)

jest bazą przestrzeni \(V\). Wektorów tych jest \(n\), a zatem wystarczy sprawdzić ich liniową niezależność.

Niech

\(\begin{array} {rcl} \alpha _1w_1+...+\alpha _mw_m+&& \beta _1v_1+...+\beta _kv_k\\&&+\gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0. \end{array}\) (2.5)

Obłóżmy tę równość przez \(f\). Dostajemy równość

\(\alpha _1\tilde f(w_1)+...+\alpha _m\tilde f(w_m)=-\beta _1\tilde w _1-...-\beta _k\tilde w_k.\) (2.6)

Korzystając z uwagi poprzedzającej dowodzone twierdzenie wiemy, że obie strony równości (2.6) muszą być zerami. A zatem \(\beta _1,...,\beta _k\) są równe zeru. Wracamy teraz do równości (2.5). Mamy

\(\alpha _1w_1+...+\alpha _mw_m+ \gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0.\) (2.7)

Zatem

\(\gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}\in im f\cap ker f.\)

Pamiętając o tym, jak zostały wybrane wektory \(u_1,...,u_{n-m-k}\), otrzymujemy, że \(\gamma _1u_1 +...+\gamma _{n-m-k}u_{n-m-k}=0\). Wynika stąd, że \(\gamma_1=...=\gamma _{n-m-k}=0\). Wracając teraz do równości (2.7) otrzymujemy, że \(\alpha _1=...=\alpha _m =0\).

Na koniec zauważmy, że baza 2.4 jest bazą Jordana dla \(f\). Widać to natychmiast, jeśli ułożymy ją następująco. Na początku

\(u_1,...,u_{n-m-k}, w_{i_1},...,\tilde w_{1}, v_1,w_{i_2},...,\tilde w_2, v_2,..., w_{i_k},..., \tilde w_k,v_k\)

a potem pozostałe wektory ciągu \(w_1,..., w_n\) w takiej kolejności jak były.

Jeśli \(0\) nie jest wartością własną endomorfizmu \(f\) (\(f\) jest monomorfizmem), to weźmy pewną wartość własną \(\lambda\). Ponieważ wielomian charakterystyczny rozkłada się na czynniki stopnia 1, wartość własna istnieje. Zamiast \(f\) rozważmy endomorfizm \(F=f-\lambda I\). Na podstawie powyższego dowodu wiemy, że istnieje baza Jordana dla \(F\). Baza Jordana dla \(F\) jest też bazą Jordana dla \(f=F+\lambda I\).

Wniosek 2.3

Dla każdego endomorfizmu przestrzeni zespolonej istnieje baza i macierz Jordana.

Informatyka MIMUW