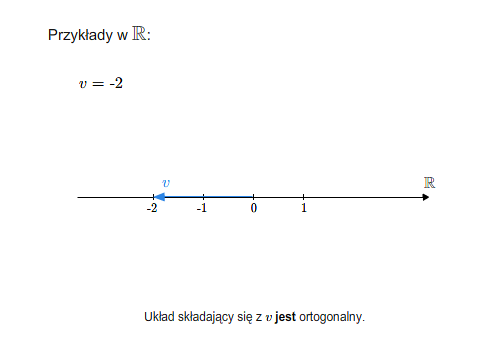Informatyka MIMUW

(1.1)

Normę wektora nazywamy też jego długością. Stosowany jest zapis \(v^2\), który oznacza \(v\cdot v\) lub, co na jedno wychodzi, \(\Vert v\Vert ^2\).

Sprawdzenie, że funkcja zdefiniowana formułą (1.1) spełnia warunki N1) i N2) jest natychmiastowe. Warunek trójkąta sprawdzimy po udowodnieniu następującej nierówności Schwarza.

Twierdzenie 1.5 [Nierówność Schwarza]

Dla funkcji określonej wzorem (1.1) i każdych dwóch wektorów \(v,w\in V\) zachodzi nierówność

\(| v\cdot w |\le \Vert v\Vert\Vert w\Vert .\)      (1.2)

Równość w powyższej nierówności zachodzi wtedy i tylko wtedy, gdy wektory \(v\), \(w\) są liniowo zależne.

Dowód

Jeśli któryś z wektorów \(v\), \(w\) jest zerowy, to twierdzenie jest oczywiste. Załóżmy więc, że wektory te są niezerowe.

Rozważmy funkcję zmiennej rzeczywistej \(t\)

\(f(t)= \Vert tv +w\Vert ^2.\)

Funkcja ta przybiera wartości nieujemne. Z drugiej strony mamy

\(f(t)=t^2\Vert v\Vert ^2 +2t(v\cdot w) +\Vert w \Vert ^2.\)

A zatem funkcja \(f(t)\) jest trójmianem kwadratowym przyjmującym wartości nieujemne, którego współczynnik przy \(t^2\) jest dodatni. Oznacza to, że wyróżnik \(\Delta\) jest niedodatni. Wobec tego

\(\Delta =4(v\cdot w) ^2 -4\Vert v\Vert ^2\Vert w\Vert ^2\le 0,\)

czyli \((v\cdot w) ^2\le \Vert v\Vert ^2 \Vert w\Vert ^2\). Po spierwiastkowaniu tej nierówności dostajemy nierówność Schwarza.

Dla udowodnienia drugiej tezy zauważmy najpierw, że jeśli \(v=\lambda w\), to oczywiście w (1.2) mamy równość. Odwrotnie, równość w (1.2) oznacza, że wyróżnik trójmianu \(f(t)\) jest równy \(0\) i, co za tym idzie, istnieje \(t_o\), takie, że \(f(t_o)=0\). To zaś oznacza, że \(t_ov+w=0\), czyli \(v\), \(w\) są liniowo zależne.

Korzystając, miedzy innymi, z nierowności Schwarza otrzymujemy teraz, dla dowolnych wektorów \(v\), \(w\), ciąg równości i nierówności

\(\begin{aligned}\Vert v+w \Vert ^2&= (v+w)(v+w) =\Vert v\Vert ^2 +2v\cdot w +\Vert w\Vert ^2\\ &\le \Vert v\Vert ^2 +2 | v\cdot w | +\Vert w\Vert ^2\le \Vert v\Vert ^2 +2 \Vert v\Vert \Vert w \Vert +\Vert w\Vert ^2\\ &= (\Vert v\Vert +\Vert w\Vert )^2\end{aligned}\)

Udowodniliśmy więc nierówność trójkąta N 2) dla funkcji (1.1).

Przy okazji zauważmy, że otrzymaliśmy twierdzenie Pitagorasa. Mianowicie, jeśli wektory \(v\), \(w\) są do siebie prostopadłe, czyli \(v\cdot w=0\), to

\(\Vert v+w\Vert ^2 =\Vert v\Vert ^2 +\Vert w\Vert ^2.\)

Jeśli wektory \(v\), \(w\) sa niezerowe, to liczbę rzeczywistą \(\alpha\in [0,\pi )\) taką, że

\(\cos \alpha ={{v\cdot w}\over {\Vert v\Vert \Vert w\Vert}},\)

nazywamy kątem między wektorami \(v\) i \(w\).

Układy ortogonalne. Proces Grama - Schmidta. Bazy ortonormalne

---

Mówimy, że wektory są do siebie prostopadłe (ortogonalne), jeśli ich iloczyn skalarny jest równy \(0\). Ogólniej, układ wektorów \(v_1,..., v_n\) nazywa się układem ortogonalnym, jeśli każde dwa wektory tego układu są do siebie prostopadłe, tzn. \(v_i\cdot v_j=0\) dla \(i\ne j\). Oczywiście wektor zerowy jest prostopadły do każdego wektora. Dowolny zbiór (niekoniecznie skończony) nazywa się ortogonalny, jeśli każde dwa wektory tego zbiory są ortogonalne.

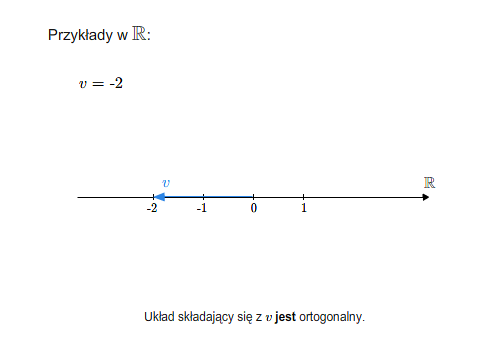
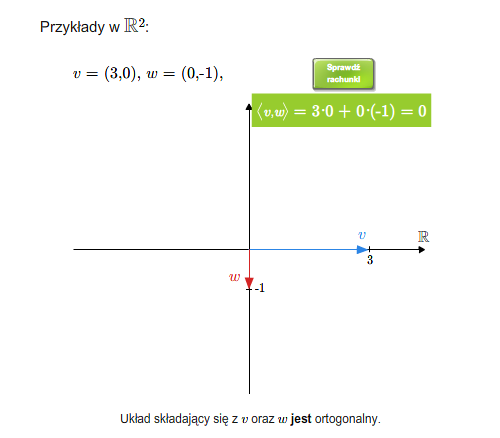
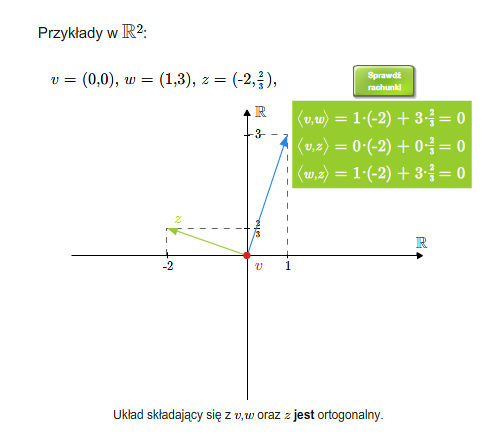
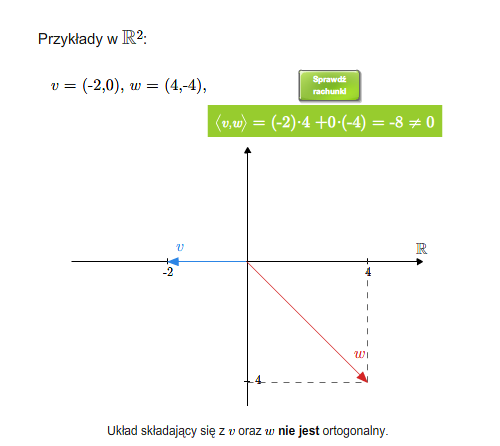
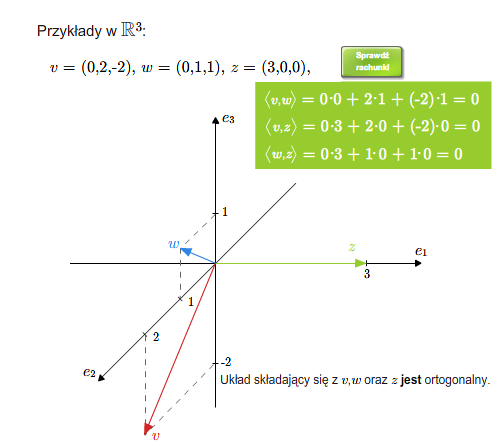
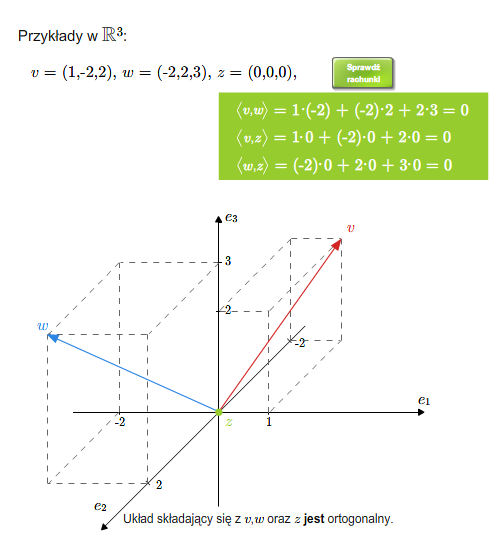
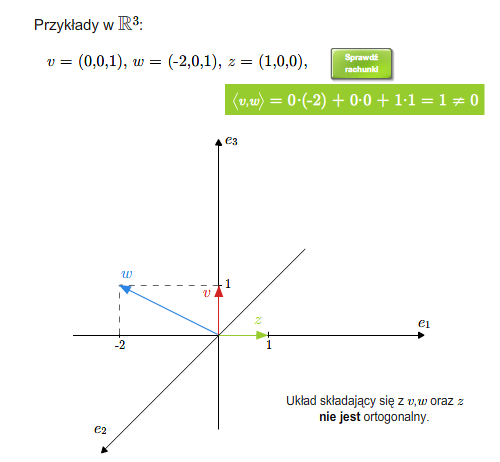Wektory ortogonalne (prostopadłe)

Mamy następujący

Lemat 2.1

Ortogonalny i nie zawierający zera układ wektorów \(v_1,...,v_n\) jest liniowo niezależny.

Dowód

Niech \(\lambda _1v_1+...+\lambda _nv_n=0\). Obie strony tej równości pomnóżmy skalarnie przez \(v_i\), dla \(i=1,..., n\). Otrzymujemy równość \(\lambda _i (v_ i\cdot v_i)=0\), a stąd \(\lambda _i=0\).

Wektor \(v\in V\) nazywa się jednostkowym, jeśli \(\Vert v\Vert =1\). Układ wektorów \(v_1,...,v_n\) nazywa się ortonormalnym, jeśli każdy z tych wektorów jest jednostkowy, a cały układ jest ortogonalny. Jeśli \(v\) jest wektorem niezerowym, to

\({v\over{\Vert v\Vert}}\)

jest wektorem jednostkowym. Mówimy, że wektor \(v\) został znormalizowany.

Niech \(v_1,...,v_n\) będzie pewnym układem liniowo niezależnym przestrzeni wektorowej \(V\) wyposażonej w iloczyn skalarny. Niech

\(e_1 = {{v_1}\over {\Vert v_1\Vert}}.\)

Wektor \(e_1\) jest jednostkowy i generuje tę samą przestrzeń co \(v_1\). Zdefiniujmy teraz wektor \(e_2\) następująco

\(\tilde e_2= v_2- (v_2\cdot e_1)e_1.\)

Łatwo sprawdzić, że wektor ten jest prostopadły do \(e_1\). Ponadto układ wektorów \(e_1, \tilde e_2\) rozpina tę samą podprzestrzeń co układ wektorów \(v_1,v_2\). Co więcej, jeśli oznaczymy przez \(V_2\) tę podprzestrzeń, to \(e_1,\tilde e_2\) oraz \(v_1,v_2\) są takimi bazami tej przestrzeni \(V_2\), że macierz przejścia od bazy \(v_1,v_2\) do bazy \(e_1, \tilde e_2\) ma wyznacznik dodatni.

Definiujemy teraz

\(e_2 ={{\tilde e_2}\over {\Vert\tilde e_2\Vert}}\)

Oczywiście układy \(v_1, v_2\) i \(e_1,e_2\) rozpinają tę samą podprzestrzeń \(V_2\), układ \(e_1, e_2\) jest ortonormalny a macierz przejścia od bazy \(v_1, v_2\) do bazy \(e_1, e_2\) przestrzeni \(V_2\) ma wyznacznik dodatni.

Załóżmy, że zdefiniowaliśmy już \(k\) kolejnych wektorów \(e_1,...,e_k\) takich, że układy \(e_1,...,e_k\) i \(v_1,..., v_k\) rozpinają tę samą podprzestrzeń \(V_k\), układ \(e_1,...,e_k\) jest ortonormalny a macierz przejścia od bazy \(v_1,..., v_k\) do bazy \(e_1,...,e_k\) ma wyznacznik dodatni. Definiujemy wektor \(\tilde e_{k+1}\) wzorem

\(\tilde e_{k+1} = v_{k+1}-(v_{k+1}\cdot e_1)e_1-...-(v_{k+1}\cdot e_k)e_k.\)      (2.3)

Następnie definiujemy

\(e_{k+1}= {{\tilde e_{k+1}}\over {\Vert \tilde e_{k+1}\Vert }}.\)

Łatwo widać, że \(\tilde e_{k+1}\) jest prostopadły do każdego z wektorów \(e_1,...,e_k\), a zatem układ \(e_1,...,e_{k+1}\) jest ortonormalny. Łatwo tez widać, że układy \(v_1,...,v_{k+1}\); \(e_1,...,e_{k+1}\) rozpinają tę samą podprzestrzeń, powiedzmy \(V_{k+1}\). Ponadto macierz przejścia od bazy \(v_1,...,v_{k+1}\) do bazy \(e_1,...,e_{k+1}\) przestrzeni \(V_{k+1}\) ma wyznacznik dodatni.

Powyższy proces otrzymywania układu ortonormalnego nazywa się procesem Grama-Schmidta. Jeśli \(v_1,...,v_k\) jest układem ortonormalnym, to proces Grama-Schmidta nie zmienia tego układu.

Proces Grama-Schmidta

Z powyższych rozumowań wynika natychmiast

Twierdzenie 2.2

Każda skończenie wymiarowa przestrzeń wektorowa wyposażoną w iloczyn skalarny ma bazę ortonormalną.

Od tego momentu do końca niniejszego wykładu zakładamy, że przestrzenie wektorowe są skończenie wymiarowe.

Jeżeli \(e_1,...,e_n\) jest bazą ortonormalną przestrzeni euklidesowej \(V\), to wektor \(v\in V\) wyraża się jako kombinacja liniowa wektorów tej bazy następującym wzorem

\(v=(v\cdot e_1)e_1+...+(v\cdot e_n)e_n.\)      (2.4)

Aby sprawdzić ten wzór wystarczy pomnożyć skalarnie obie strony tej równości przez kolejne wektory bazy \(e_1,..., e_n\).

Rzutowanie prostokątne. Izometrie

---

Niech dana będzie podprzestrzeń wektorowa \(U\) przestrzeni euklidesowej \(V\). Podprzestrzeń ta jest wyposażona w indukowany iloczyn skalarny, tzn. jest to iloczyn skalarny będący zawężeniem iloczynu skalarnego z \(V\) do \(U\) (dokładniej mówiąc, zawężeniem \(V\times V\) do \(U\times U\)). Zdefiniujmy podprzestrzeń

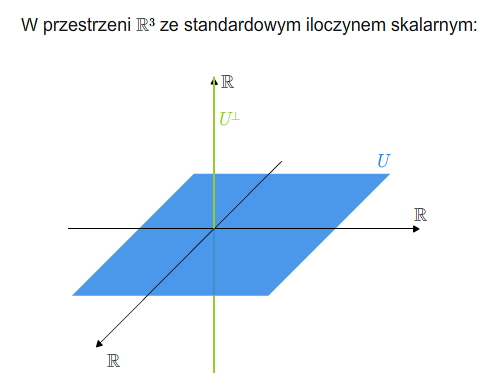
\(U^{\perp }=\{ w\in V |\ \ w\cdot v =0 \ {\rm dla\ kazdego\ v\in V}\}.\)

Łatwo sprawdzić, że \(U^{\perp}\) jest podprzestrzenią wektorową. Ponadto, \(U^{\perp}\cap U=\{0\}\). Istotnie, jeśli \(v\in U^{\perp}\cap U\), to \(v\cdot v =0\), a stąd wynika, że \(v=0\).

Niech \(v_1,...,v_k\) będzie bazą podprzestrzeni \(U\). Rozrzerzmy tę bazę do bazy \(v_1,...,v_k, v_{k+1},..., v_n\) przestrzeni \(V\). Zastosujmy do tej bazy proces Grama-Schmidta. Otrzymujemy bazę ortonormalną \(e_1,...,e_n\) przestrzeni \(V\). Pierwszych \(k\) wektorów tej bazy rozpina podprzestrzeń \(U\), pozostałe rozpinają pewne dopełnienie algebraiczne do \(U\) i należą do podprzestrzeni \(U^{\perp}\). A zatem \(U^{\perp}\) jest dopełnieniem algebraicznym do \(U\). Podprzestrzeń \(U^{\perp}\) nazywa się dopełnieniem ortogonalnym (prostopadłym) do \(U\).

Przypomnijmy, że dopełnienia algebraiczne nie są wyznaczone jednoznacznie. Dopełnienie ortogonalne (istniejące tylko w przestrzeni wyposażonej w iloczyn skalarny) jest wyznaczone jednoznacznie. Oto kilka podstawowych własności dopełnienia ortogonalnego:

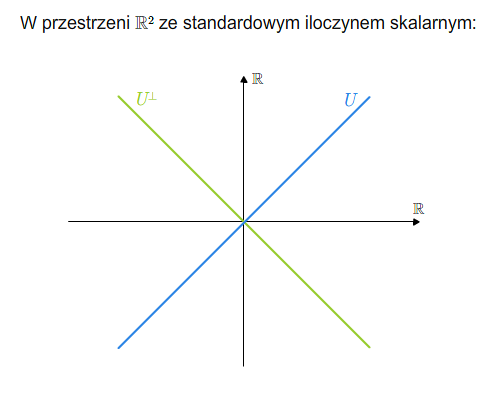
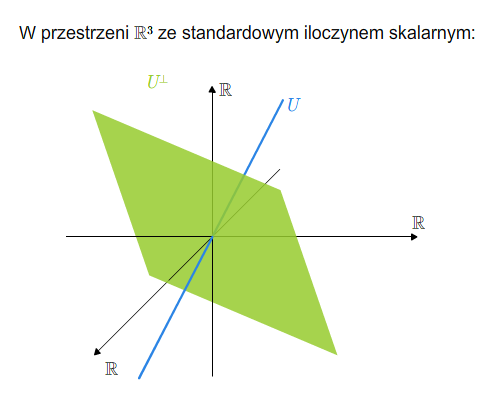
Dopełnienie ortogonalne (prostopadłe) Rzutowanie prostokątne

Lemat 3.1

Dla każdych podprzestrzeni \(U\), \(W\) przestrzeni euklidesowej \(V\) zachodzą następujące związki.

1. \((U^{\perp})^{\perp}=U\).
2. Jeżeli \(U\subset W\), to \(W^{\perp}\subset U^{\perp}\).
3. \((U+W)^{\perp}=U^{\perp}\cap W^{\perp}\).
4. \((U\cap W)^{\perp}=U^{\perp}+W^{\perp}\).

Udowodnienie powyższych własności pozostawiamy jako ćwiczenie.

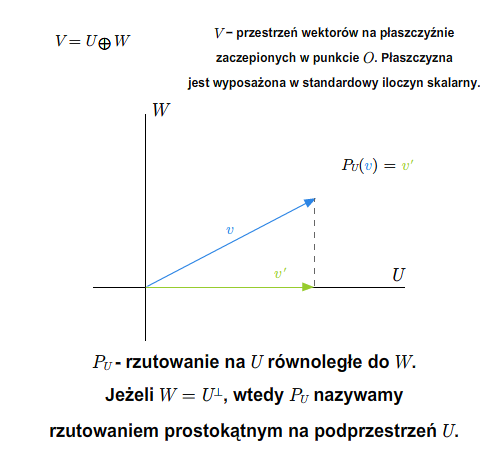
W przestrzeni euklidesowej dla ustalonej podprzestrzeni \(U\) mamy

\(V=U\oplus U^{\perp}.\)

A zatem mamy rzutowanie na \(U\) równoległe do \(U^{\perp}\). Ponieważ dopełnienie ortogonalne jest wyznaczone jednoznacznie, więc wymienianie przestrzeni \(U^{\perp}\) jest niekonieczne. Używamy określenia " rzutowanie prostokątne na podprzestrzeń \(U\) ". Podkreślmy, że możemy mówić o rzutowaniu prostokątnym tylko w przypadku przestrzeni wyposażonych w iloczyn skalarny.

Niech teraz \(V\) i \(W\) będą przestrzeniami wektorowymi wyposażonymi w iloczyny skalarne - obydwa oznaczane kropką. Mówimy, że odwzorowanie \(f:V\longrightarrow W\) jest izometrią, jeśli zachowuje iloczyn skalarny, tzn. dla każdych wektorów \(u,v \in V\) zachodzi równość \(f(u\cdot v)=f(u)\cdot f(v)\). Oczywiście odwzorowanie, które zachowuje iloczyn skalarny zachowuje też normę, czyli \(\Vert f(v)\Vert=\Vert v\Vert\) dla każdej izometrii \(f\).

Twierdzenie 3.2 [O izometrii]

Izometria jest odwzorowaniem liniowym. Co więcej, jest monomorfizmem.

Dowód

Załóżmy, że \(e_1,...,e_n\) jest bazą ortonormalną przestrzeni wektorowej \(V\). Ponieważ odwzorowanie \(f\) zachowuje iloczyn skalarny, więc wektory

\(f(e_1),...,f(e_n)\)

stanowią układ ortonormalny w \(W\), a więc jest to układ liniowo niezależny. Jest wiec bazą ortonormalną przestrzeni \({\rm im} f\). Na podstawie wzoru (2.4) i faktu, że \(f(v)\cdot f(e_i)=v\cdot e_i\) dla każdego \(i=1,...,n\), mamy

\(\begin{aligned} f(v)&=(f(v)\cdot f(e_1))f(e_1) +...+(f(v)\cdot f(e_n))f(e_n)\\ &= (v\cdot e_1)f(e_1)+...+(v\cdot e_n)f(e_n). \end{aligned}\)

Oznacza to, że jeśli \(v=\lambda _1e_1+...\lambda _ne_n\), to

\(f(v) =\lambda _1 f(e_1)+...+\lambda _n f(e_n).\)

Łatwo sprawdzić, że takie odwzorowanie jest liniowe.

Jeśli \(f(v)=0\), to \(\Vert f(v)\Vert =0\). A zatem \(\Vert v \Vert =\Vert f(v)\Vert =0\), czyli \(v =0\). W ten sposób udowodniliśmy monomorficzność \(f\).

Twierdzenie 3.3

Odwzorowanie liniowe zachowujące normę jest izometrią.

Dowód

Niech \(f\) będzie odwzorowaniem spełniającym założenia twierdzenia. Zachodzą równości

\(\Vert v+w\Vert ^2= \Vert v\Vert ^2 +2 v\cdot w +\Vert w\Vert ^2,\)

\(\Vert f(v+w)\Vert ^2 = \Vert f(v)+f(w)\Vert ^2 = \Vert f(v)\Vert ^2+ 2f(v)\cdot f(w) +\Vert f(w)\Vert ^2.\)

Ponieważ \(\Vert f(v+w)\Vert = \Vert v+w\Vert\), \(\Vert f(v)\Vert =\Vert v\Vert\) i \(\Vert f(w)\Vert =\Vert w\Vert\), więc \(f(v)\cdot f(w)= v\cdot w\).

Dowód kolejnego twierdzenia jest standardowy i pozostawiamy go czytelnikowi.

Twierdzenie 3.4

Złożenie izometrii jest izometrią. Jeśli izometria jest bijekcją, to odwzorowanie odwrotne do izometrii jest izometrią.

Niech \(f:V\longrightarrow V\) będzie izometrią przestrzeni euklidesowej \(V\). Niech \(e_1,...,e_n\) będzie bazą ortonormalną przestrzeni \(V\). Wiemy, że \(f(e_i)\cdot f(e_j)=e_i\cdot e_j \delta _{ij}\), dla \(i,j=1,...,n\). Jeśli więc \(A\) jest macierzą \(f\) przy bazie ortonormalnej, to

\(A^*A=I.\)

Macierz spełniającą powyższy warunek nazywa się macierzą ortogonalną. Macierz taką można też traktować jako izometrię przestrzeni \({\mathbb R} ^n\) wyposażonej w standardowy iloczyn skalarny. Zbiór wszystkich macierzy ortogonalnych wymiarów \(n\) na \(n\) stanowi podgrupę grupy ogólnej \(GL(n;{\mathbb R} )\). Podgrupę tę nazywa się grupą ortogonalną i oznacza przez \(O(n)\).

Dla macierzy ortogonalnej mamy \({\rm det} A^*{\rm det} A =1\). A zatem \(({\rm det} A)^2=1\), czyli \({\rm det} A= \pm 1\).

Zbiór wszystkich macierzy ortogonalnych wymiarów \(n\) na \(n\) o wyznaczniku dodatnim (czyli o wyznaczniku 1) stanowi podgrupę grupy ortogonalnej.