Informatyka MIMUW

Własności euklidesowych przestrzeni afinicznych

Jeżeli \(X\) jest przestrzenią afiniczną o kierunku \(V\) i \(V\) jest euklidesową przestrzenią wektorową, to przestrzeń \(X\) nazywamy euklidesową przestrzenią afiniczną.

Mając wybrany punkt bazowy mamy też bijekcję \(\Phi _{{\rm o}} : X\longrightarrow V\) zdefiniowana w 2. paragrafie Wykładu XIII. Za pomocą tej bijekcji można przenieść nie tylko strukturę przestrzeni wektorowej z \(V\) na \(X\), ale także iloczyn skalarny. Tak jak w przypadku struktury liniowej, przeniesiony iloczyn skalarny w istotny sposób zależy od wyboru punktu bazowego.

W euklidesowej przestrzeni afinicznej właściwym pojęciem geometrycznym jest odległość punktów, którą definiujemy przy pomocy normy wektora. Mianowicie, dla dowolnych punktów \(x,y\in X\) odległość \(d(x,y)\) definiujemy wzorem

Łatwo sprawdzić, że jest to dobrze zdefiniowana funkcja odległości.

Mówimy, że wektor \(v\in V\) jest prostopadły do podprzestrzeni afinicznej \(X_0\), jeśli \(v\) jest prostopadły do każdego wektora kierunku tej podprzestrzeni.

Twierdzenie 15.1

Niech \(X_0\) będzie podprzestrzenią afiniczna przestrzeni \(X\). Dla każdego punktu \(x\in X\) istnieje dokładnie jeden punkt \(x'\in X_0\) taki, że \(\overrightarrow { xx'}\) jest prostopadły do \(X_0\). Dla każdego punktu \(y\in X_0\) zachodzi nierówność

przy czym równość zachodzi wtedy i tylko wtedy, gdy \(y=x'\).

Dowód

Niech \(V_0\) będzie kierunkiem \(X_0\). Niech \(x_0\in X_0\) i \(x\in X\). Niech \(V_0^{\perp}\) będzie dopełnieniem ortogonalnym do \(V_0\). Rozłóżmy wektor \(\overrightarrow {x_0x}\) na sumę wektorów \(v+w\), gdzie \(v\in V_0\) i \(w\in V_0^{\perp}\). Zdefiniujmy

Punkt ten należy do \(X_0\). Ponadto

A zatem \(\overrightarrow {xx'}\) jest prostopadły do \(X_0\).

Załóżmy, że \(x''\in X_0\) jest również takim punktem, że \(\overrightarrow {xx''}\in V_0^{\perp}\). Zachodzą równości

Z drugiej strony \(\overrightarrow {x'x''}\in V_0\), bo oba punkty \(x',x''\) należą do \(X_0\). A zatem \(x'=x''\).

Niech \(y\in X_0\). Wtedy \(\overrightarrow {xy} =\overrightarrow {xx'}+ \overrightarrow {x'y}\). Składniki sumy po prawej stronie tej równości są prostopadłe, a zatem, z twierdzenia Pitagorasa, mamy

A zatem \(d^2(x,y)\ge d^2(x,x')\) i równość zachodzi wtedy i tylko wtedy, gdy \(y=x'\).

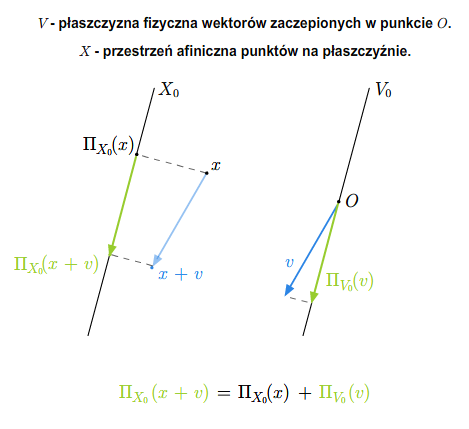
Odwzorowanie \(X \ni x\longrightarrow x'\in X_0\) nazywamy rzutowaniem prostokątnym na podprzestrzeń \(X_0\). Oznaczmy to odwzorowanie przez \(\Pi _{X_0}\). Punkt \(x'=\Pi _{X_0}(x)\) można otrzymać jako przecięcie \(X_0\) i podprzestrzeni \(x+V_0^{\perp}\).

Liczbę \(d(x,x')\) nazywamy odległością punktu \(x\) od podprzestrzeni \(X_0\). Oznaczać ją będziemy przez \(d(x,X_0)\).

Twierdzenie 15.2

Rzutowanie prostokątne w euklidesowej przestrzeni afinicznej \(X\) jest odwzorowaniem afinicznym indukującym rzutowanie prostokątne w przestrzeni \(V\).

Dowód

Niech \(\Pi _{V_0}\) oznacza rzutowanie prostokątne na podprzestrzeń wektorową \(V_0\). Z dowodu poprzedniego twierdzenia wiemy, że \(x' =x_0 + v\), gdzie \(\overrightarrow {x_0x}=v+w\) i \(v\in V_0\), \(w\in V_0^{\perp}\). Niech \(z\in V\) i \(z =z'+z''\), gdzie \(z'\in V_0\) i \(z''\in V_{0}^{\perp}\).

Zachodzą następujące równości

Zatem

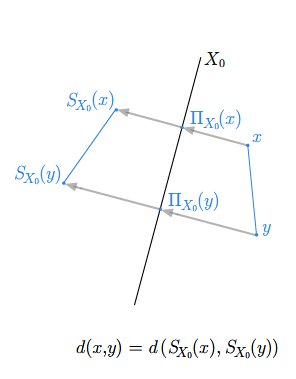
Zdefiniujemy teraz odbicie symetryczne względem podprzestrzeni \(X_0\). Definiujemy to odwzorowanie formułą

Odwzorowanie \(S_{X_0}\) nazywa się też symetrią względem podprzestrzeni \(X_0\).

Twierdzenie 15.3

Odbicie symetryczne względem podprzestrzeni jest odwzorowaniem afinicznym.

Dowód

Twierdzimy, że symetria \(S_{X_0}\) indukuje odwzorowanie liniowe \(\varphi\) zdefiniowane wzorem

Niech \(z\in V\) będzie dowolnym wektorem i niech \(z=z'+z''\), gdzie \(z'\in V_0\), \(z''\in V_0^{\perp}\). Oznaczmy przez \(x'\) punkt \(\Pi _{X_0}(x)\). Zachodzą następujące równości

Izometrią euklidesowej przestrzeni afinicznej \(X\) nazywamy odwzorowanie zachowujące odległość, tzn. odwzorowanie \(f:X\longrightarrow X\) takie, że dla każdych \(x,y\in X\) zachodzi równość

Jest oczywiste, że odwzorowanie afiniczne indukujące izometrię liniową jest izometrią. Istotnie, wystarczy zauważyć, że jeśli \(f\) indukuje izometrię \(\varphi\), to

Zachodzi też twierdzenie odwrotne.

Twierdzenie 15.4

Izometria jest odwzorowaniem afinicznym indukującym izometrię liniową.

Dowód

Niech \(o\in X\) będzie ustalonym punktem przestrzeni \(X\). Niech dane będą dwa dowolne wektory \(v,w\in V\). Oznaczmy przez \(x,y\) punkty \(o+v\) i \(o+w\) odpowiednio. Definiujemy odwzorowanie \(\varphi :V\longrightarrow V\) formułą

Zachodzą równości

Porównując te równości i korzystając z tego, że \(f\) zachowuje odległość punktów otrzymujemy równość

dla dowolnych wektorów \(v,w\in V\). Z Twierdzenia 1.10 z Wykładu X wiemy, że \(\varphi\) jest odwzorowaniem liniowym. Pozostaje więc zauważyć, że

dla dowolnych \(x\) i \(z\). W tym celu zauważamy, że zachodzą równości

Twierdzenie 15.5

Odbicie symetryczne jest izometrią.

Dowód

Korzystamy z dowodu Twierdzenia 15.3. Mamy równość \(2z'-z= z'-z''\) i kolejne równości (pamiętamy, że \(z'\cdot z''=0\))

A zatem \(\varphi\) jest odwzorowaniem liniowym zachowującym normę. Jest więc izometrią liniową.

Na koniec tego paragrafu podamy bez dowodu

Twierdzenie 15.6

Każda izometria \(n\)-wymiarowej afinicznej przestrzeni euklidesowej \(X\) jest złożeniem co najwyżej \(n+1\) odbić symetrycznych względem hiperpłaszczyzn.

Analityczny opis podprzestrzeni afinicznej podprzestrzeni euklidesowej

Rozważmy \(n\)-wymiarową afiniczną podprzestrzeń euklidesową. Bez utraty ogólności możemy założyć, że jest to przestrzeń afiniczna \({\mathbb R}^n\) o kierunku \({\mathbb R} ^n\) wyposażonym w standardowy iloczyn skalarny. W przypadku wymiarów \(2\) i \(3\) można też myśleć o tych przestrzeniach jako o znanych ze szkoły płaszczyźnie i trójwymiarowej przestrzeni fizycznej z ustalonym prostokątnym układem współrzędnych.

Przypomnijmy, że hiperpłaszczyzna afiniczna jest opisana jednym równaniem liniowym

gdzie któryś ze skalarów \(a_1,...,a_n\) jest różny od \(0\), czyli \(a_1^2+...+a_n^2\ne 0\). Jeśli wszystkie te skalary są równe zeru, to równanie opisuje całą przestrzeń \({\mathbb R} ^n\) lub zbiór pusty. W dalszych rozważaniach zakładamy, że zadane równania nie będą opisywały tego typu trywialnych sytuacji. Równanie (2.2) nazywa się równaniem ogólnym hiperpłaszczyzny. W przypadkach \(n=2\), \(n=3\) rozpoznajemy znane ze szkoły równania ogólne prostej na płaszczyźnie i płaszczyzny w trójwymiarowej przestrzeni.

Kierunek hiperpłaszczyzny danej równaniem (2.2) jest dany równaniem jednorodnym

A zatem, jeśli oznaczymy

to hiperpłaszczyzna wektorowa (2.3) jest równa

Wektor \(a\) jest prostopadły do hiperpłaszczyzny. Ponieważ \(a\) jest niezerowy, rozpina prostą prostopadłą do danej hiperpłaszczyzny wektorowej. Wektor \(a\) jest prostopadły do przestrzeni afinicznej (2.2).

Ogólniej, mówimy, że dwie podprzestrzenie afiniczne są prostopadłe, jeżeli ich kierunki są prostopadłe, czyli każde dwa wektory wzięte z tych podprzestrzeni (różnych) są prostopadłe.

Jeśli układ równań liniowych

ma rozwiązanie, to opisuje \((n-k)\)-wymiarową podprzestrzeń afiniczną \(L\) przestrzeni \({\mathbb R} ^n\), gdzie \(k={\rm rk} A\) i \(A=[a_{ij}]\in M(m,n;{\mathbb R})\) jest macierzą układu (2.4). Każde z równań opisuje hiperpłaszyznę (zgodnie z umową zakładamy, że zadane równania ogólne nie opisują sytuacji trywialnych) i koniunkcja \(m\) równań opisuje zbiór będący przecięciem tych hiperpłaszczyzn. Układ (2.4) nazywamy równaniem krawędziowym podprzestrzeni \(L\).

Każdy z wektorów

jest prostopadły do przestrzeni \(L\). Wektory te generują dopełnienie ortogonalne do kierunku podprzestrzeni \(L\) opisanego układem równań

Oczywiście, jeśli \(m>k\) oznacza to, że w układzie (2.2) są równania niepotrzebne a wektory \(a_1,..., a_m\) są liniowo zależne. Na ogół, podprzestrzeń zadana jest najmniejszą możliwą liczbą równań, czyli \(m=k\). W szczególności, prosta w trójwymiarowej przestrzeni jest zadana dwoma równaniami. Prosta taka jest krawędzią przecięcia dwóch płaszczyzn.

Każda hiperpłaszczyzna jest zbiorem rozwiązań pewnego równania liniowego, a każda \(n-m\)-wymiarowa podprzestrzeń \(L\) jest zbiorem rozwiązań pewnego układu \(m\) równań. Istotnie, niech \(V\) oznacza kierunek przestrzeni \(L\). Weźmy dopełnienie ortogonalne \(V^{\perp}\) do podprzestrzeni \(V\). Niech \(a_1,...,a_m\) będzie bazą \(V^{\perp}\). Kierunek \(V\) dany jest układem równań (2.6), gdzie \(a_{ij}\) dane są przez (2.5). Przypuśćmy, że dany jest jakiś punkt podprzestrzeni \(L\), np. punkt o współrzędnych \((b_1,...,b_n)\). Wstawiamy te współrzędne do układu (2.4) w miejsce \(x_1,..., x_n\) i otrzymujemy wyrazy wolne \(a_{10},...,a_{m0}\).

Równanie ogólne dla danej hiperpłaszczyzny nie jest jedyne. Można je pomnożyć przez niezerowy skalar i otrzymać inne równanie (proporcjonalne do poprzedniego) opisujące tę samą hiperpłaszczyznę. Jest to jedyna dowolność jaka tu występuje. Istotnie, dla danej hiperpłaszczyzny \(L\) dopełnienie ortogonalne do jej kierunku jest \(1\)-wymiarowe, a zatem generowane przez wektory proporcjonalne. W przypadku równania krawędziowego dowolność jest znacznie większa. Na przykład, łatwo widać, że prosta w trójwymiarowej przestrzeni może być krawędzią przecięcia rozmaitych układów płaszczyzn. Równanie ogólne hiperpłaszczyzny, w którym wektor \(a=(a_1,...,a_n)\) jest jednostkowy nazywa się równaniem normalnym hiperpłaszczyzny.

Niech \(L\) będzie \(k\)-wymiarową podprzestrzenią o kierunku \(V\). Niech teraz \(v_1,...,v_k\) będzie bazą podprzestrzeni wektorowej \(V\). Niech dany będzie pewien punkt \(x_0=(x_{01},...,x_{0n})\) podprzestrzeni afinicznej \(X\). Wiemy, że \(X=x_0+V\) a \(V\) jest zbiorem wszystkich kombinacji liniowych wektorów \(v_1,...,v_k\). A zatem podprzestrzeń \(L\) jest zbiorem punktów o współrzędnych \((x_1,...,x_n)\) wyrażonych wzorami

gdzie \((v_{i1},...,v_{in})\) są współrzędnymi wektora \(v_i\) dla \(i=1,...,k\) i \(t_1,..., t_k\) są parametrami przebiegającymi zbiór \({\mathbb R}\). Równanie to może też być zapisane bez użycia współrzędnych, tzn. w postaci

Układ (2.7) lub równanie (2.8) nazywa się równaniem parametrycznym podprzestrzeni \(L\). W szczególności, mamy równanie parametryczne prostej (jest jeden parametr) i równanie parametryczne płaszczyzny (są dwa parametry). Zamiana równania parametrycznego na ogólne lub krawędziowe (dla danej podprzestrzeni) jak również operacja odwrotna będą przerobione na ćwiczeniach.

Dysponujemy już metodą na znajdowanie rzutu prostokątnego punktu na podprzestrzeń afiniczną.

Załóżmy, że mamy \((n-m)\) - wymiarową podprzestrzeń \(L\) daną równaniem krawędziowym (lub ogólnym) (2.4) (lub (2.2)). Mamy więc wektory prostopadłe \(a_1,...,a_m\) rozpinające przestrzeń \(V^{\perp}\).

Dany jest też punkt, powiedzmy \(p=(p_1,...,p_n)\), który chcemy zrzutować prostokątnie na podprzestrzeń. Możemy więc napisać równanie parametryczne podprzestrzeni \(L^{\perp}(p):=p+V^{\perp}\). Wstawiamy kolejne \(x_1\),...,\(x_n\) z tego równania (wyrażone przez parametry \(t_1,...,t_m\) i pewne stałe) do równania krawędziowego. Otrzymujemy układ \(m\) równań ze względu na niewiadome \(t_1,...,t_m\). Rozwiązujemy ten układ (istnieje jedno jedyne rozwiązanie, bo istnieje dokładnie jeden rzut prostokątny punktu na podprzestrzeń) i otrzymujemy parametry, które odpowiadają punktowi przecięcia podprzestrzeni \(L\) z podprzestrzenią \(L^{\perp}(p)\). Z równania parametrycznego obliczamy współrzędne punktu odpowiadającego takim parametrom.

Na przykład, niech dana będzie hiperpłaszczyzna \(L\) opisana równaniem ogólnym

i punkt \(p=(p_1,...p_n)\). Oznaczmy przez \(p'=(p'_1,...,p'_n)\) rzut prostokątny punktu \(p\) na \(L\) i przez \(a\) wektor \((a_1,...,a_n)\). Równanie parametryczne prostej prostopadłej do \(L\) i przechodzącej przez punkt \(p\) jest następujące

Po wstawieniu \(x_1,...,x_n\) do równania ogólnego dostajemy

A zatem punkt przecięcia \(L\) i \(L^{\perp}(p)\)odpowiada parametrowi

Punkt \(p'\) ma współrzędne

Jeśli podprzestrzeń \(L\) dana jest równaniem parametrycznym (2.8), to rzut prostokątny znajdujemy następująco. Wektory \(v_1,...,v_k\) traktujemy jako wektory rozpinające dopełnienie ortogonalne do \(V^{\perp}\). A zatem mamy równanie krawędziowe przestrzeni \(L^{\perp}(p)\). Wstawiając \(x_1,...,x_n\) z danego równania parametrycznego do równania krawędziowego podprzestrzeni \(L^{\perp}(p)\) otrzymujemy układ równań ze względu na niewiadome \(t_1,...,t_k\). Rozwiązujemy ten układ i rozwiązanie wstawiamy do równania parametrycznego.

Załóżmy na przykład, że dana jest prosta \(L\)

i punkt \(p=(p_1,...,p_n)\). Hiperpłaszczyzna \(L^{\perp}(p)\) prostopadła do \(L\) i przechodząca przez punkt \(p\) ma równanie ogólne

gdzie \(a_0=-v_1p_1-...-v_np_n\) i \(v=(v_1,...,v_n)\). Po wstawieniu za \(x_1,...,x_n\) wyrażeń z parametrem i rozwiązaniu równania ze względu na niewiadomą \(t\) otrzymujemy wzór na wartość parametru \(t_0\) odpowiadającego punktowi przecięcia, czyli punktowi \(p'\). Ostatecznie, rzut prostokątny \(p'\) punktu \(p\) jest dany wzorem