Informatyka MIMUW

W tym wykładzie podamy algorytmy konstrukcji automatu minimalnego i twierdzenia dowodzące ich poprawności.

Algorytmy konstrukcji automatu minimalnego

---

Dla języka rozpoznawanego $L$ konstrukcję automatu minimalnego można rozpocząć, startując z opisu języka danego na przykład przez wyrażenie regularne lub też jakiegoś automatu rozpoznającego ten język. W niniejszym wykładzie przedstawimy algorytmy konstrukcji automatu minimalnego obejmujące oba wspomniane punkty startu. Jako pierwszy, nawiązując do rezulatów przedstawionych w poprzednim wykładzie, prezentujemy algorytm, dla którego punktem wyjścia jest język $L$. Prezentację poprzedzimy wprowadzeniem pewnej operacji na słowach zwanej pochodną J.Brzozowskiego.

Definicja 1.1.

Niech $\; L \subset A^* \;$ będzie dowolnym językiem, a $\; u \in A^* \;$ dowolnym słowem. Pochodną Brzozowskiego (residuum) z języka $L$ względem słowa $u$ nazywamy język

$u^{-1}L=\{w \in A^*\;\; :\;\;\; uw \in L \}.$

Podczas obliczeń pochodnych Brzozowskiego (residuów języka $L$) można wykorzystać poniższe równości.

Niech $L_1, L_2\subset A^* \;$ będą dowolnymi językami, $a \in A$ dowolną literą, a $u,v \in A^*$ dowolnymi słowami. Prawdziwe są następujące równości:

$\begin{array}{rll}\nonumber u^{-1}(L_1 \cup L_2) & = & u^{-1}L_1 \cup u^{-1}L_2, \\ \nonumber u^{-1}(L_1 \backslash L_2) & = & u^{-1}L_1 \backslash u^{-1}L_2, \\ \nonumber u^{-1}(L_1 \cap L_2) & = & u^{-1}L_1 \cap u^{-1}L_2, \\ \nonumber a^{-1}(L_1L_2) & = & (a^{-1}L_1)L_2 \mbox{, jeśli } 1 \notin L_1, \\ \nonumber a^{-1}(L_1L_2) & = & (a^{-1}L_1)L_2 \cup a^{-1}L_2 \mbox{, jeśli } 1 \in L_1, \\ \nonumber a^{-1}L^* & = & (a^{-1}L)L^*, \\ \nonumber v^{-1}(u^{-1}L) & = & (uv)^{-1}L. \end{array}$

Przykład 1.1.

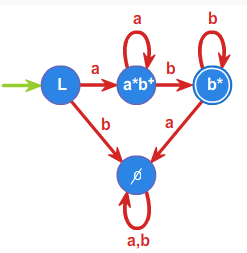
Obliczmy wszystkie pochodne dla języka $L=a^+b^+$. Okazuje się, że są tylko cztery różne pochodne liczone względem $a$, $b$, $ab$ i słowa pustego $1$. Mianowicie:

$a^{-1}L=a^*b^+$,
$b^{-1}L= \emptyset$,
$ab^{-1} L=b^*$,
$1^{-1}L=L$.

Dla wszystkich innych słów otrzymujemy uzyskane powyżej języki, co wynika z własności pochodnych (patrz wyżej wypisane równości) i z następujacych obliczeń:

$\forall n \in \mathbb{N} \quad (a^n)^{-1}L=a^*b^+$,
$\forall n \in \mathbb{N} \quad (b^n)^{-1}L= \emptyset$,
$\forall n \in \mathbb{N} \quad (ab^n)^{-1} L=b^*$.

Zauważmy również, nawiązując raz jeszcze do rezulatów przedstawionych w poprzednim wykładzie, że prawdziwa jest następująca równoważność wiążąca wprowadzone pojęcie pochodnej Brzozowskiego z prawą kongruencją syntaktyczną:

$u \;P{^r}_L\; v \Longleftrightarrow u^{-1}L=v^{-1}L.$

Rozpisując z definicji lewą stronę tej równoważności, otrzymujemy, iż dla dowolnego słowa $z \in A^*$ słowo $uz \in L$ wtedy i tylko wtedy, gdy $vz \in L$. A to równoważnie oznacza (znów z definicji), że $u^{-1}L=v^{-1}L.$

Z uzasadnionej równoważności oraz twierdzenia 3.4 o prawej kongruencji syntaktycznej z poprzedniego wykładu wnioskujemy równoważność rozpoznawalności języka $L$ i skończonej ilości różnych pochodnych Brzozowskiego tego języka.

Pierwszy z przedstawianych algorytmów będzie konstruował automat minimalny, wyznaczając prawą kongruencję automatową poprzez zastosowanie metody pochodnych Brzozowskiego. Metoda ta umożliwia przeprowadzanie odpowiednich obliczeń bezpośrednio na wyrażeniach regularnych. Ogólny opis algorytmu jest następujący. Stany konstruowanego automatu minimalnego etykietowane są zbiorami odpowiadającymi pewnym językom. Mając dany język $L$, ustanawiamy stan początkowy automatu jako $L$, wpisujemy go na listę $\mathcal{L}$ i obliczamy $a^{-1}L$ dla każdej litery $a \in A$. Jeśli wśród obliczonych wartości znajduje się język niewystępujący na liście, dodajemy go do listy. Obliczenia pochodnych Brzozowskiego wykonujemy, dopóki będziemy uzyskiwać nowe języki (nowe stany). Funkcja przejść konstruowanego automatu minimalnego zdefiniowana jest następująco:

$f(X, a)=a^{-1}X,$ gdzie $X$ jest pewnym językiem z listy $\mathcal{L}$.

Obliczone języki określają stany automatu minimalnego.

Automatem minimalnym dla automatu $\mathcal{A}=(S, A, f, s_0, T)$ będzie zatem automat

$\mathcal{A}_L=(S_L, A, f_L, s_0^L, T_L),$

gdzie:

• $S_L=\{u^{-1}L:\ u \in A^*\}$,

• $s_0^L = L$,

• $T_L = \{u^{-1}L:\ u \in L\}$,

• $f_L(u^{-1}L,a) = a^{-1}(u^{-1}L)=(ua)^{-1}L$.

Jeśli zdefiniujmy odwzorowanie $\nu: S \rightarrow S_L$, kładąc:

$\nu(s)=u^{-1}L, \mbox{ gdzie } s=f(s_0,u),$

to można dowieść, że $\nu$ jest dobrze określone, jest epimorfizmem oraz $\nu(s_0) = s_0^L$ - porównaj twierdzenie 3.1 z wykładu 4. Prawdą jest też, iż $s \in T$ wtedy i tylko wtedy, gdy $\nu(s) \in T_L$ oraz że następujący diagram komutuje:

tutaj diagram

Formalny zapis algorytmu przedstawiony jest poniżej.

Algorytm Minimalizuj1 - algorytm minimalizacji wykorzystujący pochodne Brzozowskiego

---

1 Wejście: $L$ - język
2 Wyjście: automat minimalny $\mathcal{A}'=(S_L, A, f_L, s_L, T_L)$ taki, że $L\mathcal{A}'=L$
3 $S_L \leftarrow \{L\}$;
4 włóż$(\mathcal{L},L)$;
5 while $\mathcal {L}\ne \emptyset$ do
6 $M \leftarrow$ zdejmij($\mathcal {L}$);
7 for each $a \in A$ do
8 $N \leftarrow a^{-1}M$;
9 if $N \cap S_L = \emptyset$ then
10 $S_L \leftarrow S_L \cup \{N\}$;
11 włóż$(\mathcal{L},N)$;
12 end if
13 end for
14 end while
15 for each $M \in S_L$ do
16 for each $a \in A$ do
17 $f_L(M,a) \leftarrow a^{-1}M$;
18 end for
19 end for
20 $s_L \leftarrow L$;
21 $T_L \leftarrow \{u^{-1}L:\ u \in L\}$;
22 return $\mathcal{A}'$;

Funkcja zdejmij$(\mathcal{L})$, występująca w linii 6., zdejmuje z kolejki $\mathcal{L}$ pierwszy element i zwraca go jako swoją wartość. Procedura włóż$(\mathcal{L},L)$, występująca w liniach 4. oraz 11., wstawia na koniec kolejki $\mathcal{L}$ element $L$.

Przykład 1.2.

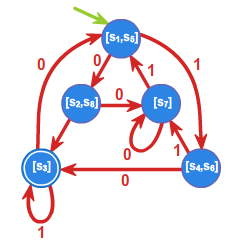
Dla języka $L=a^+b^+$ z przykładu 1.1 (patrz przykład 1.1.) w wyniku działania powyższego algorytmu otrzymamy czterostanowy automat
$\mathcal{A}_L=(S_L,A, f, L, T),$ gdzie $S_L= \{L, a^*b^+ ,\emptyset, b^*\}$, a funkcja przejść zadana jest grafem:

Rysunek 1

Prezentowane poniżej twierdzenie uzasadnia kolejny algorytm konstrukcji automatu minimalnego. Tym razem punktem wyjścia jest dowolny automat rozpoznający język $L$.

Analogicznie do konstrukcji relacji $\rho _{i}$, przedstawionej w wykładzie 4, możemy określić ciąg odpowiednich relacji na zbiorze stanów dowolnego automatu rozpoznającego język $L$. Relacje te służą do efektywnego określenia automatu minimalnego, równoważnego zadanemu.

Twierdzenie 1.1.

Niech $\mathcal{A}= (S,A,f,s_0,T)$ będzie dowolnym automatem i niech $L = L(\mathcal{A})$. Przez $\approx _\mathcal{A} \subset S \times S$ oznaczmy relację równoważności zawierającą dwie klasy równoważności $T$ i $S\setminus T$. Przez $\overline \rho_i$ dla $i\in \Bbb N$
oznaczmy zstępujący ciąg relacji określony następująco:

$\overline \rho _1 = \approx _\mathcal{A}$, a dla $i = 2,...$ przyjmijmy

$\overline \rho _i = \{ (s,t) \in \; S \times S \; : \;\; \forall a \in A \cup \{1\} \; \; f(s,a) \overline{\rho}_{i-1} f(t,a) \;\}. \;$.

Wtedy $\bigcap \overline \rho_i$ jest największą prawą kongruencją automatową zawartą w relacji $\overline \rho_1 = \approx _ \mathcal{A}$ i automat minimalny ma postać

$\mathcal{A}_{L}=\left( S/ \bigcap \overline \rho _i,A,f^*,[s_{0}],T/ \bigcap \overline \rho _i \right)$.

Dowód tego twierdzenia przebiega analogicznie do dowodu twierdzenia 3.3 z wykładu 4 (patrz twierdzenie 3.3. wykład 4).

Algorytm działajacy w oparciu o powyższe twierdzenie na podstawie zadanego automatu $A = (S, A, f, s_0, T)$, konstruuje efektywnie automat minimalny dla $\mathcal{A}$, obliczając ciąg relacji $\rho _1$. Proces konstrukcji przebiega w sposób iteracyjny. Zaczynamy od zdefiniowania relacji $\approx_\mathcal{A}$, która posiada tylko dwie klasy abstrakcji: do pierwszej z nich należą wszystkie stany końcowe, a do drugiej - wszystkie pozostałe stany. Tak więc

$\forall s, t \in S\ s \approx_\mathcal{A} t \Leftrightarrow (s \in T \wedge t \in T) \vee (s \in S \backslash T \wedge t \in S \backslash T)$.

Definiujemy pierwszą z relacji $\overline \rho$, czyli relację $\overline \rho_1$ jako równą $\approx_ \mathcal {A}$, a następnie, dla każdej obliczonej już relacji $\overline \rho_i-1$, obliczamy relację $\overline \rho_i$ w następujący sposób:

$s_1 \overline \rho_i s_2 \Leftrightarrow (s_1 \overline \rho_{i-1} s_2) \wedge (\forall a \in A\ f(s_1, a) \overline \rho_{i-1} f(s_2,a))$.

Nowo obliczona relacja $\overline \rho_i$ albo podzieli jedną lub kilka klas abstrakcji relacji $\overline \rho_{i-1}$, albo będzie identyczna z relacją $\overline \rho_{i-1}$. Jeśli zajdzie ta druga sytuacja, to znaczy, że dla każdego $j>i$ w oczywisty sposób spełniona jest równość $\overline \rho_j=\overline \rho_i$, czyli ciąg relacji ustabilizuje się. W tym momencie algorytm kończy swoje działanie i klasy abstrakcji relacji $\overline \rho_i$ będą reprezentować stany automatu minimalnego.

Algorytm Minimalizuj2 - algorytm minimalizacji automatu wykorzystujący stabilizujący się ciąg relacji

---

1 Wejście: $\displaystyle \mathcal{A}=(S, A, f, s_0, T)$ - automat taki, że $\displaystyle L=L(\mathcal{A})$.
2 Wyjście: automat minimalny $\displaystyle \mathcal{A}'=(S',A',f', s_0', T')$ dla $\displaystyle \mathcal{A}$.
3 $\displaystyle \overline{\rho}_1\displaystyle \leftarrow\displaystyle \approx_{\mathcal{A}}$;
4 $\displaystyle i \leftarrow 1$;
5 repeat
6 $\displaystyle \slash \slash$ oblicz $\displaystyle \overline{\rho}_i$: $\displaystyle s_1 \overline{\rho}_i s_2 \Leftrightarrow (s_1 \overline{\rho}_{i-1} s_2) \wedge (\forall a \in A\ f(s_1, a) \overline{\rho}_{i-1} f(s_2,a))$;
7 $\displaystyle i \leftarrow i+1$;
8 empty$\displaystyle (\overline{\rho}_i)$
9 for each $\displaystyle (s_1,s_2)\in S\times S$ do
10 flag$\displaystyle \leftarrow$true;
11 for each $\displaystyle a\in A$
12 if not $\displaystyle f(s_1, a) \overline{\rho}_{i-1} f(s_2,a)$ then
13 flag$\displaystyle \leftarrow$false;
14 end if
15 end for
16 if flag=true and $\displaystyle s_1 \overline{\rho}_{i-1} s_2$ then
17 $\displaystyle \overline{\rho}_{i} \leftarrow \overline{\rho}_{i} \cup \{(s_1,s_2)\}$;
18 end if
19 end for
20 until $\displaystyle \overline{\rho}_i = \overline{\rho}_{i-1}$
21 $\displaystyle S' \leftarrow S \slash \overline{\rho}_i$;
22 for each $\displaystyle [s]_{\overline{\rho}_i} \in S \slash \overline{\rho}_i$ do
23 for each $\displaystyle a \in A$ do
24 $\displaystyle f'([s]_{\overline{\rho}_i},a) \leftarrow [f(s,a)]_{\overline{\rho}_i}$;
25 end for
26 end for
27 $\displaystyle s_0' \leftarrow [s_0]_{\overline{\rho}_i}$;
28 $\displaystyle T' \leftarrow \{[t]_{\overline{\rho}_i}:\ t \in T\}$;
29 return $\displaystyle \mathcal{A}'=(S', A, f', s_0', T')$;

Przykład 1.3.

Zminimalizujemy automat $\displaystyle \mathcal{A}=(S,A,f,s_0,T)$, dla którego

$\displaystyle S=\left\{ s_{0},s_{1},s_{2},s_{3},s_{4},s_5 \right\}, A=\{a,b\}, T=\left\{s_1, s_{2},s_{4}\right\}$ ,

a funkcja przejść określona jest przy pomocy grafu.

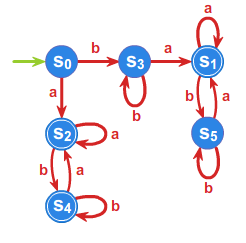
Rysunek 2

Konstruujemy ciąg relacji $\displaystyle \overline{\rho}_i$.

Na początku $\displaystyle \overline{\rho}_1$ dzieli $\displaystyle S$ na dwie klasy abstrakcji; pierwsza zawiera stany końcowe, a druga -- wszystkie pozostałe, czyli uzyskujemy dwa zbiory $\displaystyle \{s_1,s_2,s_4\}$ oraz $\displaystyle \{s_0, s_3, s_5\}$.
Obliczmy $\displaystyle \overline{\rho}_2$ (pierwszy przebieg pętli w liniach 5.-20. algorytmu). Aby dwa elementy (stany) $\displaystyle s$ i $\displaystyle t$ były ze sobą w relacji $\displaystyle \overline{\rho}_2$ muszą być ze sobą w relacji $\displaystyle \overline{\rho}_1$ oraz musi zachodzić

$\displaystyle \forall a \in A \;\; f(s, a) \overline{\rho}_1 f(t,a).$

Czyli kolejna, nowa relacja może ewentualnie podzielić już istniejące zbiory zdefiniowane przez poprzednią relację. Nie może
więc zajść taka sytuacja, że w jednej klasie abstrakcji relacji $\displaystyle \overline{\rho}_{i+1}$ znajdą się elementy z różnych klas
abstrakcji relacji $\displaystyle \overline{\rho}_i$.

Rozważmy najpierw zbiór $\displaystyle \{s_1, s_2, s_4\}$. Oczywiście każde dwa stany z tego zbioru są ze sobą w relacji $\displaystyle \overline{\rho}_1$. Zauważmy, że $\displaystyle f(s_2, a)=f(s_4,a)=s_2$, $\displaystyle f(s_2,b)=f(s_4,b)=s_4$, więc
$\displaystyle s_2 \overline{\rho}_2 s_4$ (bo $\displaystyle s_2 \overline{\rho}_1 s_2$ oraz $\displaystyle s_4 \overline{\rho}_1 s_4$). Ponieważ $\displaystyle f(s_1,b)=s_5$ i $\displaystyle f(s_2,b)=s_4$, a wiemy, że $\displaystyle s_5$ nie jest w relacji $\displaystyle \overline{\rho}_1$ z $\displaystyle s_4$, zatem stany $\displaystyle s_1$ i $\displaystyle s_2$ nie mogą być ze sobą w relacji $\displaystyle \overline{\rho}_2$, a to oznacza, że także stany $\displaystyle s_1$ i $\displaystyle s_4$ nie mogą być ze sobą w relacji $\displaystyle \overline{\rho}_2$.

W analogiczny sposób można sprawdzić, że relacja $\displaystyle \overline{\rho}_2$ nie podzieli zbioru $\displaystyle \{s_0, s_3, s_5\}$. Ostatecznie, po pierwszym wykonaniu pętli algorytmu minimalizacji obliczyliśmy relację $\displaystyle \overline{\rho}_2$, która dzieli $\displaystyle S$ na następujące podzbiory:

$\displaystyle \{s_1\}, \{s_2, s_4\}, \{s_0, s_3, s_5\}.$

W kolejnym kroku obliczamy $\displaystyle \overline{\rho}_3$. Zbiór $\displaystyle \{s_1\}$ oczywiście nie może być już podzielony na mniejsze podzbiory. Łatwo zauważyć, że $\displaystyle \overline{\rho}_3$ nie podzieli także zbioru $\displaystyle \{s_2, s_4\}$.

Rozważmy teraz zbiór $\displaystyle \{s_0, s_3, s_5\}$. Mamy $\displaystyle f(s_3, a)=f(s_5, a)$ oraz $\displaystyle f(s_3, b)=s_3$, $\displaystyle f(s_5, b)=s_5$ i wiadomo, że $\displaystyle s_3 \overline{\rho}_2 s_5$, zatem $\displaystyle s_3$ i $\displaystyle s_5$ będą ze sobą w relacji $\displaystyle \overline{\rho}_3$.

Ponieważ $\displaystyle f(s_0, a)=s_2$ i $\displaystyle f(s_3, a)=s_1$, ale $\displaystyle s_2$ i $\displaystyle s_1$ nie są
ze sobą w relacji $\displaystyle \overline{\rho}_2$, zatem nie mogą być także ze sobą w relacji $\displaystyle \overline{\rho}_3$. Relacja $\displaystyle \overline{\rho}_3$ dzieli więc zbiór $\displaystyle \{s_0, s_3, s_5\}$ na zbiory $\displaystyle \{s_0\}$ oraz
$\displaystyle \{s_3, s_5\}$.

Podział zbioru $\displaystyle S$ przez relację $\displaystyle \overline{\rho}_3$ wygląda więc

następująco:

$\displaystyle \{s_0\}, \{s_1\}, \{s_2, s_4\}, \{s_3, s_5\}.$

Relacja $\displaystyle \overline{\rho}_4$ nie podzieli już ani zbioru $\displaystyle \{s_2, s_4\}$, ani zbioru $\displaystyle \{s_3, s_5\}$, więc uzyskujemy równość $\displaystyle \overline{\rho_4}=\overline{\rho}_3$ i ponieważ ciąg relacji się ustabilizował, algorytm kończy działanie.

Podsumowując, mamy:

$\displaystyle \overline{\rho} _{1}$

$\displaystyle \{s_1, s_{2},s_{4}\}, \{s_{0},s_{3},s_5\},$

$\displaystyle \overline{\rho} _{2}$

$\displaystyle \{s_{1}\},\{s_2,s_{4}\}, \{s_{0},s_{3},s_5\},$

$\displaystyle \overline{\rho} _{3}$

$\displaystyle \{s_{1}\},\{s_2,s_{4}\}, \{s_{0}\},\{s_{3},s_5\}.\displaystyle \overline{\rho} _{3}=\overline{\rho} _{4}$ i równoważny minimalny automat $\displaystyle \mathcal{A}_L=(S,f^*,s_0,T)$ ma $\displaystyle 4$ stany.

$\displaystyle q_0=\{s_{0}\}, q_1=\{s_{1}\}, q_2 = \{s_2,s_{4}\}, q_3 =\{s_{3},s_5\}$, $\displaystyle T=\{q_1 ,q_2\}$.
Jak łatwo zauważyć jest to automat z przykładu 3.1 zamieszczonego w wykładzie 4 (patrz przykład 3.1. wykład 4).}}

Rysunek 3

Jednym z najczęściej stosowanych algorytmów automatu minimalnego jest algorytm, który buduje "tabelkę" na podstawie której określa się automat minimalny. Poprawność tego algorytmu również uzasadnia twierdzenie 1.1 (patrz twierdzenie 1.1.).

W algorytmie tym wyznaczać będziemy tzw. stany rozróżnialne. Algorytm działa w czasie $\displaystyle O(|A|n^2)$, gdzie $\displaystyle |A|$ jest mocą alfabetu, a $\displaystyle n$ -- liczbą stanów automatu wejściowego, czyli podlegajacego minimalizacji. Złożoność pamięciowa jest również $\displaystyle O(|A|n^2)$. Prezentowany algorytm nosi nazwę algorytmu Hopcrofta-Ullmana. Znana w literaturze jest pewna zmodyfikowana wersja tego algorytmu. Jest to algorytm Aho-Sethiego-Ullmana, który ma tę samą złożoność czasową, ale lepszą złożoność pamięciową - $\displaystyle O(|A|n)$. Natomiast w ramach ćwiczeń prezentujemy jeszcze jeden
algorytm, znany jako algorytm minimalizacji Hopcrofta. Czas działania tego algorytmu wynosi $\displaystyle O(n \log n)$.

Niech $\displaystyle \equiv$ będzie relacją zdefiniowaną przez funkcję przejść automatu w następujący sposób:

$\displaystyle p \equiv q \Leftrightarrow \forall w \in A^* \ (f(p,w) \in T \Leftrightarrow f(q,w) \in T).$

Definicja 1.2.

Stany $\displaystyle p$ i $\displaystyle q$ są równoważne, jeśli $\displaystyle p \equiv q$.

Jeśli stany nie są równoważne, to będziemy mówić, że są rozróżnialne.

Zadaniem algorytmu jest wyznaczenie stanów równoważnych, celem ich utożsamienia ze sobą. Algorytm musi zdecydować, dla każdej pary
stanów $\displaystyle (p,q)$, czy są one rozróżnialne. Jeśli pod koniec działania algorytmu okaże się, że nie stwierdziliśmy rozróżnialności tych
stanów, to znaczy, że są one równoważne; następuje ich utożsamienie, czyli "połączenie" ich w jeden stan. Gdy takiego połączenia dokonamy
dla wszystkich par stanów, wobec których nie stwierdziliśmy ich rozróżnialności, powstanie automat o minimalnej liczbie stanów.

W praktyce algorytm nie wyznacza stanów równoważnych, ale stany rozróżnialne, gdyż jest to po prostu łatwiejsze. Po wyznaczeniu
wszystkich par stanów rozróżnialnych pozostałe pary stanowić będą stany równoważne.

W algorytmie wykorzystywać będziemy tablicę list $\displaystyle \mathcal{L}[p,q]$, po jednej liście dla każdej pary stanów. Funkcja initialize $\displaystyle(\mathcal{L}[p,q])$ inicjalizuje listę pustą, funkcja zdejmij $\displaystyle(\mathcal{L}[p,q])$ zdejmuje jeden z elementów, natomiast funkcja włóż $\displaystyle (\mathcal{L}[p,q],x)$ wkłada element $\displaystyle x$ na listę
$\displaystyle \mathcal{L}[p,q]$. Funkcja empty $\displaystyle (\mathcal{L}[p,q])$ zwraca wartość true gdy lista jest pusta, oraz false w przeciwnym wypadku. Zwróćmy uwagę, że elementami każdej z list $\displaystyle \mathcal{L}[p,q]$ są pary stanów $\displaystyle (s,t)\in S\times S$.

Algorytm Minimalizuj3 - algorytm minimalizacji wykorzystujący relację $\displaystyle \equiv$

---

1 Wejście: $\displaystyle \mathcal{A}=(S, A, f, s_0, T)$ - automat
2 Wyjście: $\displaystyle \mathcal{A}'=(S', A, f', s_0', T')$ - automat minimalny taki, że $\displaystyle L(\mathcal{A}')=L(\mathcal{A})$.
3 for each $\displaystyle p \in T$ do
4 for each $\displaystyle q \in S \backslash T$ do
5 zaznaczone$\displaystyle [p,q] \leftarrow 1$;
6 initialize($\displaystyle \mathcal{L}[p,q]$)
7 end for
8 end for
9 for each $\displaystyle (p,q) \in (T \times T) \cup ((S \backslash T) \times (S \backslash T))$ do
10 zaznaczone$\displaystyle [p,q] \leftarrow 0$;
11 end for
12 for each $\displaystyle (p,q) \in (T \times T) \cup ((S \backslash T) \times (S \backslash T))$ do
13 flag$\displaystyle \leftarrow$false
14 for each $\displaystyle a \in A$ do
15 if zaznaczone$\displaystyle [f(p,a),f(q,a)]=1$ then
16 flag$\displaystyle \leftarrow$true;
17 end if
18 end for
19 if flag=true then
20 OZNACZ$\displaystyle (p,q)$; $\displaystyle \triangleright$ para $\displaystyle (f(p,a),f(q,a))$ była oznaczona dla pewnego $\displaystyle a$;
21 else
22 for each $\displaystyle a \in A$ do
23 if $\displaystyle f(p,a)\neq f(q,a)$ then
24 włóż$\displaystyle (\mathcal{L}[p,q],(f(p,a),f(q,a)))$;
25 end if
26 end for
27 end if
28 end for
29 $\displaystyle S' \leftarrow S \slash_\equiv$; $\displaystyle \triangleright$ relacja $\displaystyle \equiv$ jest dopełnieniem tabeli zaznaczone
30 for each $\displaystyle [s]_{ \equiv} \in S \slash_\equiv$ do
31 for each $\displaystyle a \in A$ do
32 $\displaystyle f'([s]_{\equiv},a) \leftarrow [f(s,a)]_{\equiv}$;
33 end for
34 end for
35 $\displaystyle s_0' \leftarrow [s_0]_{\equiv}$;
36 $\displaystyle T' \leftarrow \{[t]_{\equiv}:\ t \in T\}$;
37 return $\displaystyle \mathcal{A}'=(S', A, f', s_0', T')$;

Występujaca w algorytmie procedura Oznacz opisana jest poniżej.

Algorytm

---

1 procedure OZNACZ$\displaystyle (p,q \in S)$
2 if zaznaczone$\displaystyle [p,q]=1$
3 return
4 end if
5 zaznaczone$\displaystyle [p,q]\leftarrow 1$
6 while not empty$\displaystyle (\mathcal{L}[p,q])$ do
7 OZNACZ(zdejmij$\displaystyle (\mathcal{L}[p,q]))$
8 end while
9 end procedure

Działanie algorytmu łatwo przedstawić na tabelce, która złożona jest z kwadratów - pól, odpowiadających parom stanów automatu. Fakt znalezienia przez algorytm pary stanów rozróżnialnych zaznaczamy symbolem "x" w polu tabelki odpowiadającym tej parze, co wykorzystamy w przykładzie.

Przykład 1.4.

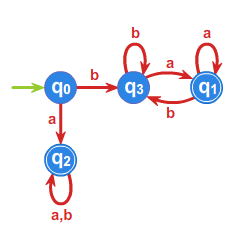
Zminimalizujemy automat przedstawiony na rysunku 4, używając algorytmu Minimalizuj3.

Rysunek 4

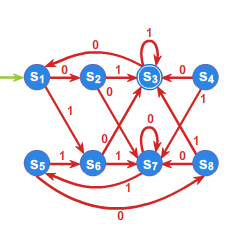
Proces działania algorytmu i konstrukcji tabelki przedstawiony jest na poniższej animacji 1.

Animacja 1

Wypełniona tabelka po zakończeniu działania algorytmu przedstawiona jest na rysunku 5.

Rysunek 5

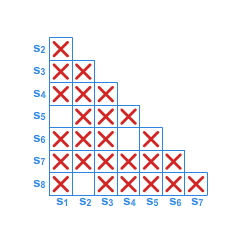
Z tabelki odczytujemy, że stanami równoważnymi są stany $\displaystyle s_1, s_5$, stany $\displaystyle s_2, s_8$ oraz stany $\displaystyle s_4, s_6$. Automat minimalny przedstawiony jest na rysunku 6.

Rysunek 6