Automat niedeterministyczny. Lemat o pompowaniu
W tym wykładzie zdefiniujemy automat niedeterministyczny, udowodnimy jego równoważność z automatem deterministycznym oraz podamy algorytm konstrukcji równoważnego automatu deterministycznego. Wprowadzimy także automaty niedeterministyczne z pustymi przejściami. W ostatniej części wykładu sformułujemy lemat o pompowaniu dla języków rozpoznawanych przez automaty skończenie stanowe.
Automat niedeterministyczny
Wprowadzony wcześniej automat jest modelem obliczeń, czy też mówiąc ogólniej, modelem procesu o bardzo prostym opisie. Stan procesu zmienia się w sposób jednoznaczny pod wpływem sygnału zewnętrznego reprezentowanego przez literę alfabetu. Opisem tych zmian jest więc funkcja. Pewnym uogólnieniem powyższej sytuacji może być dopuszczenie relacji, która opisuje zmiany stanu. W efekcie opis zmiany stanów staje się niedeterministyczny w tym sensie, że z danego stanu automat przechodzi w pewien zbiór stanów. Jak udowodnimy pó{z}niej, z punktu widzenia rozpoznawania lub poprawnych obliczeń, takie uogólnienie nie rozszerza klasy języków rozpoznawanych przez automaty.
Definicja 1.1.
Automatem niedeterministycznym nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,f),\) w którym \(\displaystyle S\) jest dowolnym zbiorem, zwanym zbiorem stanów, a \(\displaystyle f: S \times A \rightarrow \displaystyle \mathcal{P}(S)\) funkcją przejść.
Funkcję przejść rozszerzamy do funkcji \(\displaystyle f: S \times A^* \rightarrow\displaystyle \mathcal{P}(S)\) określonej na całym wolnym monoidzie \(\displaystyle A^*\) w następujący sposób:
dla każdego \(\displaystyle s \in S \;\;\;f(s,1) = \{ s\},\)
dla każdego \(\displaystyle s \in S, \;\; a \in A\) oraz dowolnego \(\displaystyle w \in A^* \;\;\; f(s,wa)=f(f(s,w),a) .\)
Zwróćmy uwagę, że prawa strona ostatniej równości to obraz przez funkcję \(\displaystyle f\) zbioru \(\displaystyle f(s,w)\) i litery \(\displaystyle a\). Funkcję przejść automatu niedeterministycznego można także traktować jako relację
W związku z powyższą definicją automat wprowadzony wcześniej, w wykładzie 3, będziemy nazywać automatem deterministycznym.
Definicja 1.2.
Język \(\displaystyle L\subset A^{*}\) jest rozpoznawalny przez automat niedeterministyczny \(\displaystyle \mathcal{A}_{ND} \displaystyle =(S,f)\) wtedy i tylko wtedy, gdy istnieje \(\displaystyle I \subset S\) -- zbiór stanów początkowych oraz \(\displaystyle F \subset S\) - zbiór stanów końcowych taki, że
Niedeterministyczny automat rozpoznający język \(\displaystyle L\) będziemy oznaczać jako system \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,A,f,I,F)\) lub \(\displaystyle \mathcal{A}_{ND}=(S,f,I,F),\) jeśli wiadomo, nad jakim alfabetem określono automat.
Na pierwszy rzut oka mogłoby się wydawać, że wprowadzony automat istotnie rozszerza możliwości automatu deterministycznego, że jego moc obliczeniowa jest istotnie większa. Okazuje się jednak, że z punktu widzenia rozpoznawania języków, czyli właśnie z punktu widzenia mocy obliczeniowej, automaty deterministyczne i niedeterministyczne są równoważne.
Twierdzenie 1.1.
Język \(\displaystyle L \subset A^*\) jest rozpoznawany przez automat deterministyczny wtedy i tylko wtedy, gdy jest rozpoznawany przez automat niedeterministyczny.
Dowód
Rozpocznijmy dowód od oczywistej obserwacji. Zauważmy, iż każdy automat deterministyczny można przekształcić w niedeterministyczny, modyfikując funkcję przejść w ten sposób, że jej wartościami są zbiory jednoelementowe. Modyfikacja ta prowadzi w konsekwencji do równoważnego automatu niedeterministycznego.
Dla dowodu implikacji w stronę przeciwną załóżmy, że język \(\displaystyle L=L(\mathcal{A}_{ND})\) , gdzie \(\displaystyle \mathcal{A}_{ND} \displaystyle = (S,f,I,F)\), jest automatem niedeterministycznym. Określamy teraz równoważny, jak się okaże, automat deterministyczny. Jako zbiór stanów przyjmujemy \(\displaystyle \mathcal{P}(S)\) , czyli ogół podzbiorów zbioru \(\displaystyle S\). Funkcję przejść \(\displaystyle \overline{f}:\mathcal{P}(S)\times A^{*}\longrightarrow \mathcal{P}(S)\) określamy kładąc dla dowolnego stanu \(\displaystyle S_1 \in\displaystyle \mathcal{P}(S)\) oraz dowolnej litery \(\displaystyle a \in A\)
a następnie rozszerzamy ją do \(\displaystyle A^{*}\) . Łatwo sprawdzić, że funkcja \(\displaystyle \overline{f}\) spełnia warunki funkcji przejść. Przyjmując następnie zbiór \(\displaystyle I \in \displaystyle \mathcal{P}(S)\) jako stan początkowy oraz zbiór \(\displaystyle T=\left\{ \mathcal{S}_{1}\in \mathcal{P}(S)\, :\, S_{1}\cap F\neq \emptyset \right\}\) , jako zbiór stanów końcowych stwierdzamy, dla określonego automatu \(\displaystyle \mathcal{A}_{D}=\left( \mathcal{P}(S),\overline{f},I,T\right)\) , równość
Skonstruowany automat jest zatem deterministyczny i równoważny wyjściowemu, co kończy dowód twierdzenia.
Uwaga 1.1.
Dla określonego w dowodzie automatu \(\displaystyle \mathcal{A}_{D}\) na ogół nie wszystkie stany są osiągalne ze stanu \(\displaystyle I\). Aby uniknąć takich stanów, które są bezużyteczne, funkcję przejść należy zacząć definiować od stanu \(\displaystyle I\) i kolejno określać wartości dla już osiągniętych stanów.
Przykład 1.1.
Automat \(\displaystyle \mathcal{A}_{ND} \displaystyle = (Q,A,f,I,F)\) nad alfabetem \(\displaystyle A=\{a,b\}\) określony przez zbiory \(\displaystyle Q=\{q_{0},q_{1},q_{2},q_4\} , I=\{q_0\}, F=\{q_{3}\}\) i
zadany poniższym grafem jest przykładem automatu niedeterministycznego.
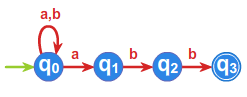
Automat ten, jak łatwo teraz zauważyć, rozpoznaje język \(\displaystyle L(\mathcal{A})=A^*abb\) .
Przedstawimy teraz algorytm, który mając na wejściu automat niedeterministyczny konstruuje równoważny automat deterministyczny.
Algorytm Determinizacja - buduje deterministyczny automat równoważny automatowi niedeterministycznemu
1 Wejście: \(\displaystyle \mathcal{A}=(S, A, f, s_0, T)\) - automat niedeterministyczny.
2 Wyjście: \(\displaystyle \mathcal{A}'=(S', A, f', s_0', T')\) - automat deterministyczny taki,
że \(\displaystyle L(\mathcal{A}')=L(\mathcal{A})\).
3 \(\displaystyle S' \leftarrow \{\{s_0\}\}\);
4 \(\displaystyle s_0' \leftarrow \{s_0\}\);
5 \(\displaystyle \mathcal{L} \leftarrow \{\{s_0\}\}\); \(\displaystyle \triangleright\displaystyle \mathcal{L}\) jest kolejką
6 while \(\displaystyle \mathcal{L} \not = \mbox{\O}\) do
7 \(\displaystyle M \leftarrow\) zdejmij \((\mathcal{L})\);
8 if \(\displaystyle T \cap M \not = \mbox{\O}\) then \(\displaystyle T' \leftarrow T' \cup \{M\}\);
9 for each \(\displaystyle a \in A\\) do
10 \(\displaystyle N \leftarrow \bigcup_{m \in M} f(m,a)\);
11 if \(\displaystyle N \not \in S'\\) then
12 \(\displaystyle S' \leftarrow S' \cup \{N\}\);
13 włóż \(\displaystyle (\mathcal{L},N)\);
14 end if
15 \(\displaystyle f'(M, a) \leftarrow N\);
16 end for
17 end while
18 return \(\displaystyle \mathcal{A}'\);
Funkcja zdejmij, występująca w linii 7., zdejmuje z kolejki element znajdujący się na jej początku i zwraca go jako swoją wartość. Procedura włóż\(\displaystyle (\mathcal{L},N)\) z linii 13. wstawia na koniec kolejki \(\displaystyle \mathcal{L}\) element \(\displaystyle N\).
Należy zauważyć, że algorytm determinizujący automat jest algorytmem eksponencjalnym. Stany wyjściowego automatu eterministycznego etykietowane są podzbiorami zbioru stanów \(\displaystyle Q\). Jeśli pewien stan \(\displaystyle q' \in Q'\) etykietowany jest zbiorem zawierającym stan końcowy z \(\displaystyle F\), to \(\displaystyle q'\) staje się stanem końcowym w automacie \(\displaystyle \mathcal{A}'\).
Z analizy algorytmu Determinacja wynika, że w ogólności zbiór stanów wyjściowego automatu deterministycznego może osiągać wartość rzędu \(\displaystyle O(2^n)\), gdzie \(\displaystyle n\) jest ilością stanów automatu niedeterministycznego.
Zastosujemy powyższy algorytm do uzyskania automatu deterministycznego równoważnego automatowi z przykładu 1.1. (patrz przykład 1.1.) Kolejne etapy działania ilustruje zamieszczona tu animacja 1.
Automaty niedeterministyczne z przejściami pustymi
Rozszerzenie definicji automatu skończenie stanowego do automatu niedeterministycznego nie spowodowało, jak wiemy, zwiększenia mocy obliczeniowej takich modeli. Nasuwać się może pytanie, czy dołączenie do tego ostatniego modelu możliwości wewnętrznej zmiany stanu, zmiany stanu bez ingerencji sygnału zewnetrznego, czyli bez czytania litery nie zwiększy rodziny jezyków rozpoznawanych.
Model taki, zwany automatem z pustymi przejściami (w skrócie: automat z p-przejściami), zdefiniujemy poniżej.
Definicja 2.1.
Automatem niedeterministycznym z pustymi przejściami nad alfabetem \(\displaystyle A\) nazywamy system \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,f),\) w którym \(\displaystyle S\) jest dowolnym zbiorem, zwanym zbiorem stanów, a \(\displaystyle f: S \times (A \cup \{1\}) \rightarrow \displaystyle \mathcal{P}(S)\) funkcją przejść.
Uwaga 2.1.
Słowo puste \(\displaystyle 1\) występuje w powyższej definicji w dwóch rolach. Pierwsza, to znana nam rola elementu neutralnego katenacji słów. Druga, to rola jakby "dodatkowej" litery, która może powodować zmianę aktualnego stanu automatu na inny. Ponieważ słowo puste może wystąpić przed i po każdej literze dowolnego słowa \(\displaystyle w \in A^*\) (i to wielokrotnie), dlatego też czytając słowo \(\displaystyle w\), automat zmienia stany zgodnie nie tylko z sekwencją liter tego słowa, ale także z uwzględnieniem tej drugiej roli słowa pustego.
Rozszerzając powyższą definicję poprzez dodanie zbioru stanów początkowych i zbioru stanów końcowych, uzyskamy niedeterministyczny automat z pustymi przejściami \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,A,f,I,F),\) dla którego będziemy mogli zdefiniować język rozpoznawany. W tym celu określimy najpierw działanie takiego automatu pod wpływem dowolnego słowa \(\displaystyle w \in A^*\). Jeśli \(\displaystyle s \in S\) oraz \(\displaystyle w=a \in A\), to
Zwróćmy uwagę, iż zbiór określający wartość rozszerzonej funkcji jest skończony i efektywnie obliczalny, bo zbiór stanów automatu jest skończony. Jeśli teraz \(\displaystyle s \in S\) oraz \(\displaystyle w=ua \in A\), to
Stany ze zbioru \(\displaystyle f(s,w)\) będziemy nazywać stanami osiągalnymi z \(\displaystyle s\) pod wpływem słowa \(\displaystyle w\). Prawdziwe jest następujące twierdzenie, które orzeka, iż z punktu widzenia rozpoznawania automaty niedeterministyczne z pustymi przejściami rozpoznają dokładnie te same języki, co automaty niedeterministyczne.
Twierdzenie 2.1.
Język \(\displaystyle L \subset A^*\) jest rozpoznawany przez automat niedeterministyczny z pustymi przejściami wtedy i tylko wtedy, gdy jest rozpoznawany przez automat niedeterministyczny.
Dowód
(szkic) Fakt, że język \(\displaystyle L\) rozpoznawany przez automat niedeterministyczny jest rozpoznawany przez automat niedeterministyczny z pustymi przejściami jest oczywisty.
Dowód implikacji w drugą stronę polega na takiej modyfikacji automatu niedeterministycznego z pustymi przejściami rozpoznającego jezyk \(\displaystyle L\), by uzyskać automat bez pustych przejść i nie ograniczyć ani nie zwiększyć jego możliwości rozpoznawania. Zarysujemy ideę tej konstrukcji. Niech \(\displaystyle \mathcal{A}{^p}_{ND} \displaystyle = (S,A,f,I,F),\) będzie automatem niedeterministycznym z pustymi przejściami akceptującym język \(\displaystyle L\). W konstruowanym automacie pozostawiamy zbiór stanów i zbiór stanów początkowych \(\displaystyle I\) bez zmian. Jeśli z któregoś ze stanów początkowych z \(\displaystyle I\) jest możliwość osiągnięcia jakiegoś stanu końcowego z \(\displaystyle F\), to dodajemy stan początkowy do zbioru stanów końcowych, czyli zbiór stanów końcowych w konstruowanym automacie ma postać \(\displaystyle F \cup I\). Jeśli nie ma takiej możliwości, to zbiór stanów końcowych pozostaje niezmieniony. Określamy wartość funkcji przejść dla dowolnego stanu \(\displaystyle s \in S\) i litery \(\displaystyle a \in A\) jako zbiór wszystkich stanów osiągalnych ze stanu \(\displaystyle s\) pod wpływem \(\displaystyle a\). Tak skonstruowany automat niedeterministyczny nie ma pustych przejść i jak można wykazać, indukcyjnie ze względu na długość słowa, rozpoznaje dokładnie język \(\displaystyle L\).
Algorytm usuwania przejść pustych i prowadzący do równoważnego automatu niedeterministycznego przedstawiony jest w ćwiczeniach do tego wykładu.
Lemat o pompowaniu
Jedną z wielu własności języków rozpoznawanych przez automaty skończone, i chyba jedną z najważniejszych, przedstawia prezentowane poniżej twierdzenie, zwane tradycyjnie w literaturze lematem o pompowaniu. Istota własności "pompowania" polega na tym, iż automat, mając skończoną ilość stanów, czytając i rozpoznając słowa dostatecznie długie, wykorzystuje w swoim działaniu pętlę, czyli powraca do stanu, w którym znajdował się wcześniej. Przez taką pętlę automat może przechodzić wielokrotnie, a co za tym idzie, "pompować" rozpoznawane słowo, prowadzając do niego wielokrotnie powtarzane podsłowo odpowiadające tej pętli.
Twierdzenie 3.1. (Lemat o pompowaniu)
Niech \(\displaystyle L \subset A^*\) będzie językiem rozpoznawalnym. Istnieje liczba naturalna \(\displaystyle N \geq 1\) taka, że dowolne słowo \(\displaystyle { w} \in L\) o długości \(\displaystyle \mid { w} \mid \geq N\) można rozłożyć na katenację \(\displaystyle { w} = { v}_1 { u v}_2,\) gdzie \(\displaystyle { v}_1 , { v}_2 \in A^*, { u}\in A^+\), \(\displaystyle \mid {v_{1}u} \mid \leq N\) oraz
Dowód
Niech \(\displaystyle L=L(\mathcal{A})\) , gdzie \(\displaystyle \mathcal{A} \displaystyle =(S,A, f,s_0,T)\) jest deterministycznym automatem skończenie stanowym. Niech \(\displaystyle N = \#S\) i rozważmy dowolne słowo \(\displaystyle { w } = a_1....a_k \in L\) takie, że \(\displaystyle \mid { w} \mid \geq N\). Oznaczmy:
Słowo \(\displaystyle w\) jest akceptowane przez automat \(\displaystyle \mathcal{A}\) , więc \(\displaystyle s_k \in T.\) Ponieważ \(\displaystyle \#S = N\) oraz \(\displaystyle k = \mid { w} \mid \geq N\), to istnieją \(\displaystyle i,j\in \{1,...,N\}\), \(\displaystyle i< j\) takie, że \(\displaystyle s_i =s_j\).
Przyjmując teraz \(\displaystyle { v}_1 = a_1...a_i ,\;\;\; { v}_2 = a_{j+1}...a_k , \;\;\; { u} =a_{i+1}...a_j,\) dochodzimy do nastepującej konkluzji:
A to oznacza, że słowo \(\displaystyle v_{1}u^{k}v_{2}\) jest rozpoznawane przez automat \(\displaystyle \mathcal{A}\) dla dowolnej liczby \(\displaystyle k\geq 0\) , co kończy dowód. Nierówność \(\displaystyle \mid {v_{1}u} \mid \leq N\) wynika w oczywisty sposób z przyjętego na początku dowodu założenia, że \(\displaystyle N = \#S\).
Istotę dowodu przedstawia następująca animacja 2.
Wniosek 3.1.
Jeśli rozpoznawalny język \(\displaystyle L \subset A^*\) jest nieskończony, to istnieją słowa \(\displaystyle { v}_1 , { u}, { v}_2 \in A^*\) takie, że
Wniosek 3.2.
Jeśli rozpoznawalny język \(\displaystyle L \subset A^*\) nie jest zbiorem pustym, to istnieje słowo \(\displaystyle w\in L\) takie, że \(\displaystyle \mid w\mid <N\) , gdzie \(\displaystyle N\) jest stałą występującą w lemacie o pompowaniu.
Jeśli słowo \(\displaystyle w\in L\) i \(\displaystyle \mid w\mid \geq N\) , to zgodnie z lematem o pompowaniu możemy przedstawić słowo \(\displaystyle w\) jako \(\displaystyle w=v_{1}uv_{2}\) , gdzie \(\displaystyle u\neq 1\) oraz \(\displaystyle v_{1}u^{i}v_{2}\in L\) dla \(\displaystyle i=0,1,2\ldots\) . Przyjmując \(\displaystyle i=0\) , mamy \(\displaystyle v_{1}v_{2}\in L\) i \(\displaystyle \mid v_{1}v_{2}\mid <\mid w\mid\) . Powtarzając powyższy rozkład skończoną ilość razy, otrzymamy słowo należące do języka \(\displaystyle L\) , o długości mniejszej od \(\displaystyle N\) .
Lemat o pompowaniu wykorzystuje się najczęściej do uzasadnienia faktu, iż pewne języki nie są rozpoznawane przez automaty skończone. Przyjrzyjmy się bliżej technice takiego uzasadnienia.
Przykład 3.1.
Rozważmy język \(\displaystyle L = \{ a^n b^n : n \geq 0 \}\) nad alfabetem \(\displaystyle A = \{ a,b\}\). W oparciu o lemat o pompowaniu wykażemy, że język \(\displaystyle L\) nie jest rozpoznawany. Dla dowodu nie wprost, przypuszczamy, że \(\displaystyle L\) jest rozpoznawany. Na podstawie udowodnionego lematu istnieją zatem słowa \(\displaystyle { v}_1 , { u}, { v}_2 \in A^*\) takie, że \(\displaystyle { v}_1 u^* { v}_2 \subset L\) oraz \(\displaystyle { u} \neq 1.\) Biorąc pod uwagę formę słów języka \(\displaystyle L\) , wnioskujemy, że
- słowo \(\displaystyle { u}\) nie może składać się tylko z liter \(\displaystyle a\), gdyż słowo \(\displaystyle { v}_1 { u}^2 { v}_2\) zawierałoby więcej liter \(\displaystyle a\) niż \(\displaystyle b\),
- słowo \(\displaystyle { u}\) nie może składać się tylko z liter \(\displaystyle b\), gdyż słowo \(\displaystyle { v}_1 { u}^2 { v}_2\) zawierałoby więcej liter \(\displaystyle b\) niż \(\displaystyle a\),
- słowo \(\displaystyle { u}\) nie może składać się z liter \(\displaystyle a \; i \; b\), gdyż w słowie \(\displaystyle { v}_1 { u}^2 { v}_2\) litera \(\displaystyle b\) poprzedzałaby literę \(\displaystyle a\).
Ponieważ słowo \(\displaystyle { v}_1 { u}^2 { v}_2,\) należy do języka \(\displaystyle L\) , więc każdy z wyprowadzonych powyżej wniosków prowadzi do sprzeczności.