Informatyka MIMUW

W wykładzie udowodnimy twierdzenie Kleene'ego, które orzeka, że rodzina języków regularnych jest identyczna z rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Przedstawimy własności języków regularnych i gramatyk typu (3). Na koniec uzasadnimy, że rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3), są tożsame.

Twierdzenie Kleene

---

Wiemy już, z poprzednich wykładów, że rodzina wyrażeń regularnych określa rodzinę języków regularnych. Celem pierwszej części tego wykładu jest ustalenie związku pomiędzy rodziną języków regularnych a rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Twierdzenie, udowodnione przez S.C.Kleene'ego w roku 1956, orzeka, iż te dwie rodziny języków są identyczne.

Twierdzenie 1.1.

Dla dowolnego skończonego alfabetu \(\displaystyle A\)

\(\displaystyle \mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})\)

Dowód

Dowód pierwszej części twierdzenia, czyli inkluzja \(\displaystyle \mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})\) , będzie
prowadzony zgodnie ze strukturą definicji rodziny języków regularnych \(\displaystyle \mathcal{REG}(A^{*})\) .

1. Język pusty \(\displaystyle \emptyset\) jest rozpoznawany przez dowolny automat \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,s_0,T),\) w którym zbiór stanów końcowych \(\displaystyle T\) jest pusty.

2. Język a złożony z dowolnej litery \(\displaystyle a \in A\) jest rozpoznawany przez automat

Rysunek 1

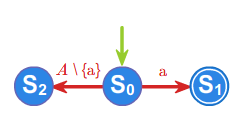
Dla dalszej części dowodu ustalmy, iż dane są języki \(\displaystyle L_1, L_2\) rozpoznawane odpowiednio przez automaty deterministyczne \(\displaystyle \mathcal{A}_{i} \displaystyle = (S_i,f_i,{s_0}^i,T_i)\), gdzie \(\displaystyle i=1,2.\)

3. Sumę mnogościową języków \(\displaystyle L_1, L_2\), czyli język \(\displaystyle L = L_1 \cup L_2\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,{s_0},T)\), dla którego \(\displaystyle S = S_1 \times S_2\), \(\displaystyle s_0 = ({s_0}^1,{s_0}^2)\), \(\displaystyle \: \displaystyle T = T_1 \times S_2\; \cup \;S_1 \times T_2\) oraz dla dowolnego stanu \(\displaystyle (s_{1},s_{2})\in S\) i litery \(\displaystyle a\in A\) funkcja przejść określona jest równością

\(\displaystyle f((s_{1},s_{2}),a)=(f_{1}(s_{1},a),f_{2}(s_{2},a)).\)

4. Katenację języków \(\displaystyle L_1, L_2\), czyli język \(\displaystyle L = L_1 \cdot L_2\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,{s_0},T)\), dla którego \(\displaystyle S=S_{1}\times \mathcal{P}(S_{2}),\quad s_{0}=\left( s_{0}^{1},\emptyset \right)\) oraz dla dowolnego stanu \(\displaystyle (s_1,S'_2) \in S\) i litery \(\displaystyle a\in A\) funkcja przejść określona jest następująco:

\(\displaystyle f((s_1,S'_2),a) = \left\{ \begin{array} {ll} (f_1(s_1,a),f_2(S'_2,a)) & \textrm{gdy} \displaystyle f_1(s_1,a) \notin T_1\displaystyle ,\\ (f_1(s_1,a),f_2(S'_2,a) \cup \{ {s_0}^2\}) & \textrm{gdy}\displaystyle f_1(s_1,a) \in T_1, \displaystyle \end{array} \right.\)

a zbiorem stanów końcowych jest

\(\displaystyle T=S_{1}\times \left\{ S'\in \mathcal{P}(S_{2})\, :\, S'\cap T_{2}\neq \emptyset \right\} .\)

5. Załóżmy, że język \(\displaystyle L\) rozpoznaje automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\). Określimy automat niedeterministyczny, który będzie rozpoznawał gwiazdkę Kleene języka \(\displaystyle L\), czyli \(\displaystyle L^*.\) Automat niedeterministyczny \(\displaystyle \mathcal{A}' \displaystyle =(S,f',\{ s_0\},T)\), w którym

\(\displaystyle f'(s,a) = \left\{ \begin{array} {ll} \{ f(s,a)\} & \textrm{gdy} \displaystyle f(s,a) \notin T\displaystyle ,\\ \{ f(s,a),s_0 \} & \textrm{gdy} \displaystyle f(s,a) \in T\displaystyle \end{array} \right.\)

rozpoznaje język język \(\displaystyle L^+.\) Dowód tego faktu jest indukcyjny i pozostawiamy go na ćwiczenia. Zauważmy teraz, że język \(\displaystyle \{1\}\) rozpoznaje automat

Rysunek 2

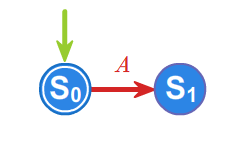
Ponieważ \(\displaystyle L^{*}=L^{+}\cup \left\{ 1\right\}\) , to korzystając z udowodnionej już zamkniętości języków rozpoznawanych
ze względu na sumę mnogościową, stwierdzamy, że istnieje automat rozpoznający język \(\displaystyle L^*\).

Zatem dowód inkluzji \(\displaystyle \mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})\) jest zakończony.

Przejdziemy teraz do dowodu inkluzji \(\displaystyle \mathcal{REG}(A^{*})\supseteq \mathcal{RE}C(A^{*})\) .

Niech \(\displaystyle L\) oznacza dowolny język rozpoznawany przez automat \(\displaystyle \mathcal{A} \displaystyle = (S,f,s_0,T).\) Dowód polega na rozbiciu języka \(\displaystyle L\) na fragmenty, dla których stwierdzenie, że są to języki regularne będzie dość oczywiste. Natomiast sam język \(\displaystyle L\) będzie wynikiem operacji regularnych określonych na tych właśnie fragmentach. Poniżej przeprowadzamy defragmentację języka \(\displaystyle L.\)

Dla \(\displaystyle s,t \in S\) niech

\(\displaystyle L(s,t) = \{w \in A^* : f(s,w) = t \}.\)

Jest to język złożony ze słów, które przeprowadzają stan \(\displaystyle s\) automatu \(\displaystyle \mathcal{A}\) w stan \(\displaystyle t\) . Ogół liter alfabetu \(\displaystyle A\) przeprowadzających stan \(\displaystyle s\) w \(\displaystyle t\) oznaczymy przez

\(\displaystyle A(s,t) = \{a \in A : f(s,a) = t \}.\)

Dla stanów \(\displaystyle s,t \in S\) i zbioru \(\displaystyle S_1 \subseteq S\) niech

\(\displaystyle L(s,S_1,t) = \{ w \in A^* : f(s,w) =t, f(s,w_1) \in S_1\;:\;w= w_1v,\; w_1, v \in A^* \}.\)

Jest to język, który można przedstawić graficznie następująco:

Rysunek 3

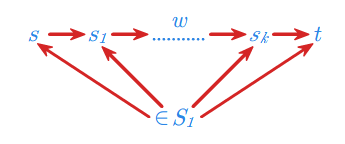
Na koniec przyjmijmy

\(\displaystyle \overline{L}(s,S_2,t) = \{ w \in A^* : f(s,w) =t, f(s,w_1) \in S_2\; : \;w = w_1v,\; w_1,v \in A^+ \},\)

określony dla \(\displaystyle S_2 \subseteq S\) i \(\displaystyle s,t \in S - S_2\)

Język ten jest graficznie interpretowany poniżej.

Rysunek 4

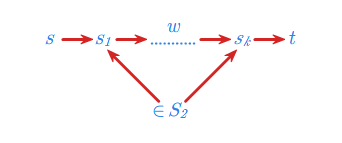
Wprost z określeń wynika, że wszystkie wprowadzone powyżej języki są regularne, czyli należą do rodziny \(\displaystyle \mathcal{REG}(A^{*})\) . Dowód tego faktu przebiega indukcyjnie ze względu na liczbę elementów zbiorów \(\displaystyle S_1\) i \(\displaystyle S_2\). Szczegóły tego dowodu pominiemy. Natomiast warto wskazać rolę, jaką spełniają w dowodzie wprowadzone wyżej języki. A mianowicie:

\(\displaystyle L(s,\left\{ s\right\} ,s)=A(s,s)^{*},\)

\(\displaystyle \overline{L}(s,\left\{ r\right\} ,t)=A(s,r)A(r,r)^{*}A(r,t),\)

\(\displaystyle L(s,S_1,t) = \overline{L}(s,S_1 \setminus \{s\},s)^*\; {\Large [}\bigcup_{r \in S_1 \setminus \{s\}}A(s,r)L(r,S_1 - \{s\},t)\;{\Large ]}.\)

Tę ostatnią równość przedstawia poniższy rysunek.

Rysunek 5

\(\displaystyle \overline{L}(s,S_2,t) = \bigcup_{r,r' \in S_2} A(s,r) L(r,S_2,r') A(r',t),\)

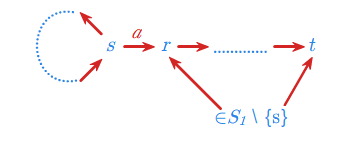
co graficznie można przedstawić następująco:

Rysunek 6

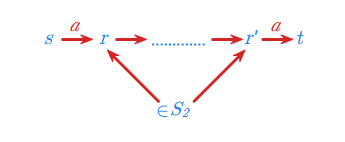
Dochodzimy więc do konkluzji, iż jezyki \(\displaystyle L(s,S_{1},t)\) oraz \(\displaystyle \overline{L}(s,S_{2},t)\) są regularne.
W szczególności zatem regularny jest język \(\displaystyle L(s_{0},S,t)=L(s_{0},t)\).

Język \(\displaystyle L\) możemy przedstawić w następującej postaci:

\(\displaystyle L = \bigcup_{t \in T} \{w \in A^* : f(s_0,w) = t \} = \bigcup_{t \in T} L(s_0,t),\)

co w połączeniu z ustaleniami punktu 3 z poprzedniej części dowodu uzasadnia tezę, że język \(\displaystyle L\) należy do rodziny \(\displaystyle \mathcal{REG}(A^{*})\).

Własności języków regularnych i gramatyk regularnych

---

W tej części wykładu omówimy własności rodziny języków i gramatyk regularnych, czyli typu (3) w hierarchii Chomsky'ego. Ustalimy też
związek pomiędzy językami a gramatykami regularnymi. Zbadamy zamkniętość rodziny języków regularnych ze względu na operacje mnogościowe, czyli ze względu na sumę, przecięcie, różnicę i uzupełnienie. Rozpoczniemy jednak tę część wykładu od wprowadzenia jednoargumentowego działania na słowach zwanego odbiciem zwierciadlanym.

Definicja 2.1.

Odbiciem zwierciadlanym słowa \(\displaystyle w = a_1 \ldots a_n \in A^*\) nazywamy słowo \(\displaystyle \stackrel{\leftarrow}{w} = a_n \ldots a_1\). Odbiciem zwierciadlanym języka \(\displaystyle L \subset A^*\) nazywamy język \(\displaystyle \stackrel{\leftarrow}{L} = \{ \stackrel{\leftarrow}{w} \in A^* \; : \; w \in L \}.\)

Twierdzenie 2.1.

Rodzina \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})\) jest zamknięta ze względu na:

(1) sumę mnogościową, przecięcie, różnicę i uzupełnienie,

(2) katenację i operację iteracji \(\displaystyle "*" ,\)

(3) obraz homomorficzny,

(4) podstawienie regularne,

(5) przeciwobraz homomorficzny,

(6) odbicie zwierciadlane.

Dowód

1. Zamkniętość rodziny języków \(\displaystyle \mathcal{REG}(A^{*})\) ze względu na sumę mnogościową wynika z twierdzenia Kleene'ego. Automat akceptujący iloczyn języków otrzymujemy, zmieniając odpowiednio zbiór stanów końcowych w automacie rozpoznającym sumę. Bowiem pozostając przy oznaczeniach punktu 3 z dowodu twierdzenia Kleene'ego, automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,{s_0},F),\) gdzie \(\displaystyle F = T_1 \times T_2\), rozpoznaje język \(\displaystyle L_1 \cap L_2.\) Jeśli automat \(\displaystyle \mathcal{A} \displaystyle =(S,f,s_0,T)\) akceptuje język \(\displaystyle L\), to automat \(\displaystyle \overline{\mathcal{A}} \displaystyle =(S,f,s_0,S\backslash T)\) akceptuje język \(\displaystyle \overline{L}=A^{*}\setminus L.\) Ostatnia własność implikuje zamkniętość ze względu na uzupełnienie.

2 Z twierdzenia Kleene'ego, punkt 4 i 5, wynika zamkniętość ze względu na katenację i operację iteracji \(\displaystyle "*"\).

3. Niech \(\displaystyle h: A^* \longrightarrow B^*\) będzie homomorfizmem. Dowód implikacji

\(\displaystyle L\in \mathcal{REG}(A^{*})\Longrightarrow \: h(L)\in \mathcal{REG}(B^{*})\)

przeprowadzimy zgodnie ze strukturą definicji rodziny języków regularnych. Dla \(\displaystyle L=\emptyset\) i dla \(\displaystyle L=\{a\}\)
gdzie \(\displaystyle a\) jest dowolną literą alfabetu \(\displaystyle A\) , implikacja jest oczywista. W pierwszym przypadku obrazem homomorficznym jest język pusty, a w drugim język \(\displaystyle \{w\}\) , gdzie \(\displaystyle w\) jest pewnym słowem nad alfabetem \(\displaystyle B\) . Dla dowolnych języków regularnych \(\displaystyle X, Y \in\displaystyle \mathcal{REG}(A^{*})\) prawdziwe są równości:

• \(\displaystyle h( X \cup Y)=h(X) \cup h(Y) \in\displaystyle \mathcal{REG}(B^{*})\) ,
• \(\displaystyle h( X \cdot Y) = h(X) \cdot h(Y) \in\displaystyle \mathcal{REG}(B^{*})\) ,
• \(\displaystyle {\displaystyle h(X^*)=h( \bigcup_{n=0} ^\infty X^n) = \bigcup_{n=0} ^\infty (h(X))^n = (h(X))^* \in}\displaystyle \mathcal{REG}(B^{*}),\)

co kończy dowód tego punktu.

4. Uzasadnienie jest podobne jak dla homomorfizmu. Jedyna różnica tkwi w tym, że dla podstawienia regularnego \(\displaystyle s:A^{*}\longrightarrow \mathcal{P}(B^{*})\) i dla dowolnej litery \(\displaystyle a \in A\) wartość podstawienia na literze jest pewnym językiem regularnym \(\displaystyle s(a)=L\in \mathcal{REG}(B^{*})\) , a nie słowem jak w przypadku homomorfizmu.

5. Niech \(\displaystyle h: A^* \longrightarrow B^*\) będzie homomorfizmem. Aby udowodnić implikację

\(\displaystyle L\in \mathcal{REG}(B^{*})\Longrightarrow \: h^{-1}(L)\in \mathcal{REG}(A^{*}),\)

odwołamy się do własności, że dla języka \(\displaystyle L \in\displaystyle \mathcal{REG}(B^{*})\) istnieje skończony monoid \(\displaystyle \; M \;\) i homomorfizm \(\displaystyle \varphi : B^* \longrightarrow M\) taki, że \(\displaystyle L = \varphi^{-1}(\varphi (L)).\) Dla

homomorfizmu \(\displaystyle \varphi \circ h : A^* \longrightarrow M\) mamy równość:

\(\displaystyle ((\varphi \circ h)^{-1} \circ (\varphi \circ h))(h^{-1} (L)) = h^{-1}(L).\)

Korzystając teraz z punktu 4 twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2. wykład 3), wnioskujemy, że
\(\displaystyle h^{-1}(L) \in\displaystyle \mathcal{REG}(A^{*})\) .

6. Wykorzystamy tutaj zapis języka regularnego przez wyrażenie regularne. Niech dla języka \(\displaystyle L \in\displaystyle \mathcal{REG}(A^{*})\) wyrażenie regularne \(\displaystyle \alpha \in \mathcal{WR}\) będzie takie, że \(\displaystyle L = \mid {\bf \alpha} \mid\). Wtedy język \(\displaystyle \stackrel{\leftarrow}{L}\) jest opisany przez wyrażenie regularne \(\displaystyle \stackrel{\leftarrow}{\bf \alpha}\), które uzyskujemy z \(\displaystyle {\bf \alpha}\) przez odbicie zwierciadlane, a dokładniej odwrócenie kolejności katenacji w każdej sekwencji tego działania występującej w wyrażeniu regularnym.

W wykładzie drugim wprowadziliśmy pojęcie gramatyki. Wracamy do tego pojęcia, a w szczególności do gramatyki typu (3), czyli regularnej. Przypomnijmy, że produkcje takiej gramatyki \(\displaystyle G=(V_N ,V_T ,v_0 ,P )\) mają postać:

\(\displaystyle v \rightarrow v' x \;\; lub \;\;\; v \rightarrow x,\)

gdzie \(\displaystyle v,v' \in V_N , \; x \in {V_T}^*\). Gramatykę typu (3), nazywamy inaczej lewostronną lub lewoliniową. Określa się też gramatykę regularną prawostronną (prawoliniową). Jest to gramatyka \(\displaystyle G=(V_N ,V_T ,v _0 ,P)\), której produkcje są postaci:

\(\displaystyle v \rightarrow xv' \;\; lub \;\;\; v \rightarrow x,\)

gdzie \(\displaystyle v,v' \in V_N , \; x \in {V_T}^*\). Jeśli język \(\displaystyle L=L(G)\) jest generowany przez gramatykę typu (3) (lewoliniową), to jego odbiciem zwierciadlanym jest \(\displaystyle \stackrel{\leftarrow}{L} =L ( \stackrel{\leftarrow}{G})\), gdzie \(\displaystyle \stackrel{\leftarrow}{G}\) jest gramatyką prawoliniową, którą uzyskuje się z gramatyki \(\displaystyle G\) przez odbicie zwierciadlane prawych stron produkcji. Oznacza to, iż zmieniamy produkcje według następujących zasad:

\(\displaystyle v \rightarrow v' x \;\;\) zastępujemy przez \(\displaystyle \;\;\; v \rightarrow \stackrel{\leftarrow}{x}v',\)

\(\displaystyle v \rightarrow x \;\;\) zastępujemy przez \(\displaystyle \;\;\; v \rightarrow \stackrel{\leftarrow}{x}.\)

Oczywiście, jeśli \(\displaystyle L\) jest językiem generowanym przez gramatykę prawoliniową, to \(\displaystyle \stackrel{\leftarrow}{L}\) jest
generowany przez odpowiednią gramatykę lewoliniową.

Podamy teraz charakterystykę rodziny języków regularnych \(\displaystyle \mathcal{REG}(A^{*})\) przez rodzinę gramatyk prawoliniowych.

Twierdzenie 2.2.

Niech \(\displaystyle L \subset A^*\). Język \(\displaystyle L \in\displaystyle \mathcal{REG}(A^{*})\) wtedy i tylko wtedy,
gdy \(\displaystyle L =L(G)\) dla pewnej gramatyki prawoliniowej \(\displaystyle G\).

Dowód

Załóżmy, że automat \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,s_0,T)\) rozpoznaje język \(\displaystyle L\) .
Definiujemy gramatykę \(\displaystyle G = (V_N , V_T , v_0 ,P)\) przyjmując \(\displaystyle V_N = S,\;\; V_T = A, \;\; v_0 = s_0\) oraz określając w następujący sposób zbiór produkcji

\(\displaystyle P = \{ s \rightarrow a f(s ,a) \; :s \in S, a \in A \} \cup \{ s \rightarrow 1 \; : s \in T \} .\)

Dla dowolnego stanu \(\displaystyle s \in S\) i słowa \(\displaystyle w \in A^+\) prawdziwa jest równoważność

\(\displaystyle s_0 \mapsto^* ws \;\; \Longleftrightarrow \;\; f(s_0 ,w) = s.\)

Dowód przeprowadzimy indukcyjnie ze względu na długość słowa \(\displaystyle w\). Niech \(\displaystyle w = a,\) dla pewnego \(\displaystyle a \in A\).
Z definicji zbioru produkcji \(\displaystyle P\) wynika równoważność

\(\displaystyle s_0 \rightarrow as \; \Longleftrightarrow \; s = f(s_0 ,a).\)

Rozważmy teraz \(\displaystyle w = a_1 \ldots a_n\) oraz \(\displaystyle s_0 \mapsto^* ws\). Z założenia indukcyjnego

wynika, że

\(\displaystyle f(s_0 , a_1 \ldots a_{n-1}) =s' \Longleftrightarrow s_0 \mapsto^* a_1 \ldots a_{n-1}s'\)

oraz, że \(\displaystyle s = f(s' ,a_n )\) wtedy i tylko wtedy, gdy \(\displaystyle s' \mapsto a_n s .\) A więc fakt, że
\(\displaystyle s=f(s_{0},w)=f(s_{0},a_{1}\ldots a_{n})=f(f(s_{0},a_{1}\ldots a_{n-1}),a_{n})\) jest równoważny temu,
że \(\displaystyle s'=f(s_{0},a_{1}\ldots a_{n-1})\mapsto a_{n}s\) . A to z kolei równoważne jest

\(\displaystyle s_{0}\mapsto^{*}a_{1}\ldots a_{n-1}s',\;\;\;s'\mapsto a_{n}s\)

i ostatecznie równoważne faktowi, że \(\displaystyle s_{0}\mapsto ^{*}a_{1}\ldots a_{n-1}a_{n}s\) .
A zatem dowodzona równoważność jest prawdziwa dla \(\displaystyle w \in A^+\), ponieważ

\(\displaystyle w\in L(\mathcal{A})\: \Longleftrightarrow \: s=f(s_{0},w)\in T\: \Longleftrightarrow \: s_{o}\mapsto ^{*}ws,\, s\rightarrow 1\in P\: \Longleftrightarrow \: w\in L(G).\)

Dla \(\displaystyle w=1\) mamy \(\displaystyle 1\in L(\mathcal{A})\: \Longleftrightarrow \: s_{0}\rightarrow 1\in P\: \Longleftrightarrow \: 1\in L(G),\) co kończy dowód w jedną stronę.

Rozważmy teraz język \(\displaystyle L = L(G)\) generowany przez pewna gramatykę prawoliniową \(\displaystyle G = (V_N , V_T , v_0 ,P)\). Skonstruujemy gramatykę równoważną \(\displaystyle G\) i taką, w której wszystkie produkcje są postaci \(\displaystyle v \rightarrow a v'\) lub \(\displaystyle v \rightarrow 1\), gdzie \(\displaystyle v,v' \in V_N , a \in A\). Będziemy zamieniać produkcje występujące w gramatyce \(\displaystyle G\) na inne, o żądanej postaci, zgodnie z następująmi zasadami:

1. Produkcje typu \(\displaystyle v \rightarrow v'\), gdzie \(\displaystyle v,v' \in V_N\)
Z symbolem nieterminalnym \(\displaystyle v \in V_N\) kojarzymy określony poniżej zbiór

\(\displaystyle V_N(v) = \{ v' \in V_N \; : \; v \rightarrow v_1 \rightarrow \ldots \rightarrow v_n \rightarrow v' \; w \; G \}\)
oraz zbiór produkcji

\(\displaystyle P(v) = \{ v \rightarrow xv" \; : \; x \neq 1 , \; \exists v' \in V_N(v) , v' \rightarrow xv" \in P \} \cup\)
\(\displaystyle \cup \{ v \rightarrow x \; : \; \exists v' \in V_N(v) , v' \rightarrow x \in P \}.\)

Dla każdego takiego symbolu \(\displaystyle v \in V_N\) usuwamy ze zbioru \(\displaystyle P\) wszystkie produkcje
\(\displaystyle v \rightarrow v'\) i wprowadzamy na to miejsce wszystkie produkcje ze zbioru \(\displaystyle P(v)\).

2. Produkcje typu \(\displaystyle v \rightarrow x\) dla \(\displaystyle x \neq 1\).

Jeśli produkcja taka występuje w \(\displaystyle P\) i \(\displaystyle x \neq 1\), to do alfabetu nieterminalnego \(\displaystyle V_N\) dodajemy nowy symbol \(\displaystyle v_x\). Następnie ze zbioru \(\displaystyle P\) usuwamy powyższą produkcję i dodajemy dwie nowe:

\(\displaystyle v \rightarrow xv_x , \;\; v_x \rightarrow 1.\)

Zauważmy, że jeśli \(\displaystyle x\neq y\), to \(\displaystyle v_x \neq v_y\).

3. Produkcje typu \(\displaystyle v \rightarrow x v'\) dla \(\displaystyle \mid x \mid > 1.\)

Jeśli \(\displaystyle v \rightarrow a_1 \ldots a_n v' \in P\), przy czym \(\displaystyle n \geq 2\), to do alfabetu
nieterminalnego \(\displaystyle V_N\) dodajemy nowe symbole \(\displaystyle v_1 , \ldots v_n\), produkcję \(\displaystyle v \rightarrow a_1 \ldots a_n v'\) usuwamy ze zbioru \(\displaystyle P\) i

dodajemy produkcje:

\(\displaystyle v \rightarrow a_1 v_1 , v_1 \rightarrow a_2 v_2 , \ldots ,v_{n-1} \rightarrow a_n v'.\)

Po opisanych powyżej trzech modyfikacjach gramatyki \(\displaystyle G\) generowany język, co łatwo zauważyć, nie ulega zmianie. Zatem
skonstruowana gramatyka jest równoważna wyjściowej. Dla otrzymanej gramatyki określamy teraz automat niedeterministyczny \(\displaystyle \mathcal{A} \displaystyle =(S,A,f,\{s_0\},T)\), przyjmując \(\displaystyle S= V_N\), \(\displaystyle A= V_T\) oraz \(\displaystyle s_0 = v_0\) i definiując następująco funkcję przejść: \(\displaystyle f(v,a) = \{ v' \in V_N \; : \; v \rightarrow av' \in P \}.\) Przjmując \(\displaystyle T = \{ v \in V_N \; : \; v \rightarrow 1 \in P \}\) jako zbiór stanów końcowych, stwierdzamy, że automat \(\displaystyle \mathcal{A}\) rozpoznaje język

\(\displaystyle L(\mathcal{A})=\{w\in V_{T}^{*}\: :\: f(s_{0})\cap T\neq \emptyset \}=L.\)

Uzyskany rezultat, w świetle równości \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{RE}C(A^{*})\) , kończy dowód twierdzenia.

Algorytmiczną stroną równoważności udowodnionej w powyższym twierdzeniu zajmiemy się w następnym wykładzie. Przykłady ilustrujące twierdzenie zamieszczamy poniżej.

Przykład 2.1.

1. Niech \(\displaystyle \mathcal{A}=(S,A,f,s_0,T)\) będzie automatem takim, że

\(\displaystyle S=\{ s_0,s_1, s_2 \}, A=\{a,b\}, T=\{s_1\}\), a graf przejść wygląda następująco:

Rysunek 7

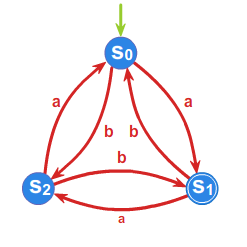
Gramatyka \(\displaystyle G=(S,A,s_0,P)\), gdzie

\(\displaystyle P=\{s_0 \rightarrow as_1, s_0 \rightarrow bs_2, s_1 \rightarrow as_2, s_1 \rightarrow bs_0, s_1 \rightarrow 1, s_2 \rightarrow as_0, s_2 \rightarrow bs_1\}\)

akceptuje język \(\displaystyle L(\mathcal{A})\).

Zauważmy, że język

\(\displaystyle L(\mathcal{A})=L(G)=\{ w \in A^* : \#_aw-\#_bw=1 mod 3\}.\)

2. Niech \(\displaystyle G=(\{v_0,v_1\},\{a,b\},v_0,P)\), gdzie

\(\displaystyle P=\{v_0 \rightarrow av_0, v_0 \rightarrow ab, v_0 \rightarrow bv_1, v_1 \rightarrow 1 \}.\)

Gramatykę \(\displaystyle G\) przekształcamy w równoważną gramatykę

\(\displaystyle G'=(\{v_0,v_1,v_2,v_b\},\{a,b\},v_0,P'),\)

gdzie

\(\displaystyle P'=\{v_0 \rightarrow av_0, v_0 \rightarrow av_2, v_0 \rightarrow bv_1 , v_2 \rightarrow bv_b, v_1 \rightarrow 1 , v_b \rightarrow 1\}.\)

Niedeterministyczny automat \(\displaystyle \mathcal{A}_{ND}=(\{v_0,v_1,v_2,v_b\},\{a,b\},f,v_0,\{v_1,v_b\})\), gdzie graf przejśc
wygląda następująco:

Rysunek 8

\(\displaystyle L(G)=L(\mathcal{A}_{ND})=a^*b\)
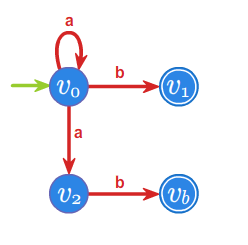
Wykorzystując udowodnione do tej pory własności rodziny języków generowanych przez gramatyki regularne, uzasadnimy teraz, iż ta
właśnie rodzina, czyli ogół języków typu (3) w hierarchii Chomsky'ego pokrywa się z rodziną \(\displaystyle \mathcal{REG}(A^{*})\) .

Twierdzenie 2.3.

Dla dowolnego alfabetu \(\displaystyle A\) rodziny języków regularnych \(\displaystyle A^{*}\) oraz języków generowanych przez gramatyki regularne są równe, czyli \(\displaystyle \mathcal{REG}(A^{*})=\mathcal{L}_{3}\) .

Dowód

Odbicie zwierciadlane dowolnego języka \(\displaystyle L\in \mathcal{REG}(A^{*})\) , czyli język \(\displaystyle \overleftarrow{L}\) należy również do rodziny \(\displaystyle \mathcal{REG}(A^{*})\) , co oznacza, że \(\displaystyle \overleftarrow{L}\in \mathcal{RE}C(A^{*})\) .
Na podstawie twierdzenia 2.2. (patrz twierdzenie 2.2.) istnieje więc gramatyka prawoliniowa \(\displaystyle G\) taka, że \(\displaystyle \overleftarrow{L}=L(G)\) . A stąd wniosek, że \(\displaystyle L=\overleftarrow{\overleftarrow{L}}=L(\overline{G})\) dla pewnej gramatyki \(\displaystyle \overline{G}\) typu (3). Zatem \(\displaystyle L\in \mathcal{L}_{3}\) .

Rozważmy teraz język \(\displaystyle L\) typu (3), czyli \(\displaystyle L=L(G)\) dla pewnej gramatyki regularnej. A więc \(\displaystyle \overleftarrow{L}=L(\overline{G})\) dla pewnej gramatyki prawoliniowej i \(\displaystyle \overleftarrow{L}\in mathcal{RE}C(A^{*})\) . Z twierdzenia Kleene'ego wynika, że \(\displaystyle \overleftarrow{L}\in \mathcal{REG}(A^{*})\) i ostatecznie \(\displaystyle L=\overleftarrow{\overleftarrow{L}}\in \mathcal{REG}(A^{*})\) , co kończy dowód twierdzenia.

Zamkniemy rozważania następującą konkluzją podsumowującą główne rezultaty tego wykładu.

Dla dowolnego skończonego alfabetu \(\displaystyle A\) prawdziwe są równości:

\(\displaystyle \mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})= \mathcal{L}_{3}\)

czyli wprowadzone pojęcia rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3) są tożsame.