Ciągi - zadania

pon., 09/13/2010 - 16:38 — ciebie

Zadanie 1.

Dany jest ciąg $(a n)$ , w którym $a 2 = 6$ , $a 5 = 15$ , $a 11 = 41$ . Czy $(a n)$ może być ciągiem arytmetycznym?

Wskazówka:

Rozwiązanie:

Zadanie 2.

Ciąg $(a n)$ jest arytmetyczny. Wiadomo, że $a 7 = 421$ i $a 16 = 124$ . Znaleźć $a 1$ i różnicę $r$ .

Wskazówka:

Rozwiązanie:

Zadanie 3.

Jak zwykle $S k$ oznacza sumę $k$ początkowych wyrazów badanego ciągu. Znaleźć wszystkie ciągi arytmetyczne $(a n)$ , w których $S 14 = 105$ i $S 16 = 136$ .

Wskazówka:

Rozwiązanie:

$S_{14} = 14a_1 + \frac{13\cdot 14}{2}r =14a_1 + 91r$,

$S_{16} = 16a_1 + \frac{15\cdot 16}{2}r =16a_1 + 120r$.

Wobec tego chcemy rozwiązać układ równań $14 a 1 + 91 r = 105$ , $16 a 1 + 120 r = 136$ . Odejmując pierwsze od drugiego, dostajemy $2 a 1 + 29 r = 31$ . Otrzymane równanie mnożymy przez 7 i odejmujemy od pierwszego. Dostaniemy $- 112 r = - 112$ , więc $r = 1$ . Stąd obliczamy $a 1 = 1$ . Otrzymaliśmy więc ciąg liczb naturalnych $a n = n$ ! Na razie wiemy tylko, że żaden inny ciąg nie spełnia warunków zadania, ale łatwo sprawdzić, że ten ciąg je spełnia. Wobec tego jest jedynym rozwiązaniem.

Zadanie 4.

Dany jest ciąg $(a n)$ , w którym $a 1 = 3$ , $a 3 = 15$ , $a 7 = 375$ , $a 9 = 1875$ . Czy $(a n)$ może być ciągiem geometrycznym?

Wskazówka:

Rozwiązanie:

Zadanie 5.

Znaleźć wszystkie ciągi geometryczne $(a n)$ o wyrazach całkowitych, dla których zachodzi $a 3 a 8 = 2048$ . Ile jest ciągów o wyrazach rzeczywistych spełniających warunki zadania?

Wskazówka:

Rozwiązanie:

Ponieważ $39 > 2048$ , to $| q | < 3$ . Oczywiście $q \neq 0$, więc pozostają do sprawdzenia 4 możliwości. Sprawdźmy:

1) $q = 2$ - wtedy $a 1 = 2$ lub $a 1 = - 2$ i obie te wartości definiują ciąg spełniający warunki zadania;

2) $q = 1$ - wtedy $a_1 = \pm \sqrt{2048}$, a to nie jest liczba całkowita;

3) $q = - 1$ - wtedy $a_1^2 = -2048 < 0$, a to niemożliwe;

4) $q = - 2$ - ten sam problem, co w punkcie 3.

Wobec tego są dwa ciągi spełniające warunki zadania, oba o ilorazie $q = 2$ , jeden z $a 1 = 2$ , drugi z $a 1 = - 2$ .

Ciągów o wyrazach rzeczywistych, spełniających daną równość, jest nieskończenie wiele - dla dowolnie wybranego $a 1$ dostajemy taki ciąg, biorąc iloraz równy $\sqrt[9]{\frac{2048}{a_1^2}}$.

Zadanie 6.

Znaleźć wszystkie ciągi geometryczne $(a n)$ , dla których zachodzi $a 1 a 13 = a 4 a 9$ .

Wskazówka:

Rozwiązanie:

Wyrażając elementy ciągu przez $a 1$ i $q$ dostajemy równość $a_1^2 q^{12} = a_1^2 q^{11}$. Możemy założyć, że $a_1 \neq 0$ i $q \neq 0$, ponieważ w przeciwnym przypadku dostalibyśmy ciąg zerowy lub prawie zerowy. Wobec tego wolno nam podzielić równość stronami przez $a_1^2 q^{11}$. Dostajemy $q = 1$ , czyli tylko ciąg stały może spełniać warunki zadania. Widać również, że każdy ciąg stały jest dobry - $a 1$ może być dowolną liczbą rzeczywistą. Wobec tego nieskończenie wiele ciągów spełnia warunki zadania.

Zadanie 7.

Znaleźć wszystkie ciągi geometryczne $(a n)$ o wyrazach całkowitych, dla których zachodzi $a 1 a 6 = 4$ i $a 2 a 3 a 4 a 5 = 16$ .

Wskazówka:

Rozwiązanie:

Zajmijmy się więc równością $a_1^2 q^5 = 4$. Oczywiście $|q| \leq 1$, ponieważ w przeciwnym przypadku $|q^5| \geq 2^5 > 4$. Gdyby $q = - 1$ , to $a_1^2 = -4 < 0$, co jest niemożliwe. Pozostaje więc $q = 1$ , i $a_1^2 = 4$ - w tym przypadku otrzymujemy więc dwa ciągi, jeden dla $a 1 = 2$ , drugi dla $a 1 = - 2$ .

Zadanie 8.

Znaleźć wszystkie ciągi geometryczne $(a n)$ , dla których zachodzi $a 1 a 8 = 3$ i $a 4 a 6 a 7 = 9$ .

Wskazówka:

Rozwiązanie:

Zadanie 9.

Znaleźć wszystkie ciągi geometryczne $(a n)$ , dla których zachodzi $a 2 a 6 a 14 = 111$ i $a 4 a 7 a 11 = 74$ .

Wskazówka:

Rozwiązanie:

Okazuje się, że warunki podane w zadaniu przypisują temu samemu wyrażeniu dwie różne wartości - otrzymujemy sprzeczność, czyli szukany ciąg nie istnieje.

Zadanie 10.

Wykazać, że jeśli $(a n)$ jest ciągiem geometrycznym, to dla dowolnych liczb naturalnych $k, m$ takich, że $m < k$ zachodzi $a_{k-m}a_{k+m} = a_k^2$.

Wskazówka:

Rozwiązanie:

Zadanie 11.

Wyznaczyć wszystkie ciągi (skończone i nieskończone) o wyrazach dodatnich, które jednocześnie są arytmetyczne i geometryczne.

Wskazówka:

Rozwiązanie:

Jeśli ciąg ma długość 1 lub 2, to spełnia definicję ciągu arytmetycznego i ciągu geometrycznego.

Załóżmy, że ciąg ma przynajmniej 3 wyrazy. Weźmy trzy kolejne wyrazy z dowolnego miejsca w ciągu. Oznaczmy je $a$ , $b$ i $c$ .

Z definicji ciągu arytmetycznego $b - a = c - b$ , czyli $b = \frac{a+c}{2}$. Z definicji ciągu geometrycznego $\frac{b}{a} = \frac{c}{b}$, czyli $b = \sqrt{ac}$. Wobec tego $\sqrt{ac} = \frac{a+c}{2}$. Po prostych przekształceniach $a - 2\sqrt{ac} + c = 0$, a więc $(\sqrt{a} - \sqrt{c})^2 = 0$, czyli $\sqrt{a} = \sqrt{c}$. (Można też skorzystać z nierówności średnich.) Stąd oczywiście $a = b = c$ .

Ponieważ dowolna trójka kolejnych wyrazów ciągu składa się z równych liczb, to wszystkie wyrazy w tym ciągu są równe.

A jaka jest odpowiedź na to pytanie, jeśli dopuścimy do rozważań ciągi o wyrazach ujemnych?

Zadanie 12.

Dany jest trójkąt prostokątny o polu 24, którego długości boków tworzą ciąg arytmetyczny. Wyznaczyć długości boków tego trójkąta.

Wskazówka:

Rozwiązanie:

Z definicji ciągu arytmetycznego $b - a = c - b$ , czyli (2) $2 b = a + c$ .

Mamy jeszcze trzecią informację - twierdzenie Pitagorasa: (3) $a 2 + b 2 = c 2$ .

Teraz trzeba tylko rozwiązać układ równań...

Przekształcając (3), dostajemy $b 2 = (c - a)(c + a)$ . Podstawiając z (2) $2 b$ zamiast $c + a$ , mamy $b 2 = 2 b (c - a)$ , czyli $\frac{b}{2} = c-a$. Odejmując tę równość od (2), otrzymujemy $a = \frac{3}{4}b$.

Teraz możemy podstawić to do (1) i dostaniemy $\frac{3}{2}b^2 = 24$, czyli $b 2 = 16$ , a więc $b = 4$ (długość boku trójkąta musi być dodatnia, więc rozwiązanie ujemne odpada).

Stąd $a = \frac{3}{4}b = 3$ i $c = 5$ - otrzymaliśmy w rozwiązaniu najbardziej znaną trójkę pitagorejską.

Zadanie 13.

Wyznaczyć długości boków trapezu, jeśli wiadomo, że dwa jego kąty są proste, najkrótszy bok ma długość 1 i długości kolejnych (na obwodzie) boków tworzą ciąg geometryczny.

Wskazówka:

1. najkrótszy bok jest podstawą,

2. najkrótszy bok to wysokość trapezu.

Warunek, że dwa kąty trapezu są proste, można przetłumaczyć na związek między długościami boków, korzystając z twierdzenia Pitagorasa.

Rozwiązanie:

1. Najkrótszy bok jest podstawą. Wówczas drugim bokiem w ciągu geometrycznym jest ten prostopadły do podstaw - oznaczmy jego długość przez $a$ . Zauważmy, że $a$ jest wobec tego ilorazem ciągu geometrycznego. Stąd długość drugiej podstawy to i czwartego boku to odpowiednio $a 2$ i $a 3$ .

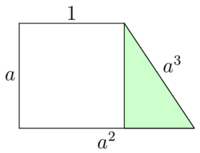
Z twierdzenia Pitagorasa otrzymujemy równość $a 2 + (a 2 - 1) 2 = a 6$ , którą można łatwo przekształcić do $a 6 - a 4 + a 2 - 1 = 0$ , czyli $(a 2 - 1)(a 4 + 1) = 0$ . Ponieważ równanie $a 4 + 1 = 0$ nie ma rozwiązań w zbiorze liczb rzeczywistych, to jedynymi możliwymi wartościami $a$ są rozwiązania równania $a 2 - 1 = 0$ , czyli 1 i $- 1$ . Oczywiście $a = - 1$ nie może być długością boku trapezu, więc pozostaje tylko rozwiązanie $a = 1$ - trapez jest kwadratem o boku 1.

2. Najkrótszy bok to wysokość trapezu. Wówczas, jeśli długość krótszej podstawy oznaczymy przez $a$ , to długości drugiej krawędzi bocznej i drugiej podstawy wynoszą odpowiednio $a 2$ i $a 3$ .

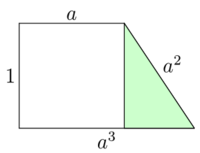
Tak jak poprzednio, korzystamy z twierdzenia Pitagorasa, otrzymując równość $1 + (a 3 - a) 2 = a 4$ , czyli po przekształceniach $(a 2 - 1)(a 4 - 2 a 2 - 1) = 0$ . W tym przypadku również dostajemy rozwiązanie $a = 1$ . Oprócz tego, rozwiązując równanie $a 4 - 2 a 2 - 1 = 0$ , otrzymujemy jeden dodatni pierwiastek $a = \sqrt{1+\sqrt{2}}$, który także jest rozwiązaniem zadania.

Zadanie 14.

Dany jest trójkąt prostokątny o obwodzie $\sqrt{3} + 1$. Wiadomo, że miary jego kątów tworzą ciąg arytmetyczny. Obliczyć długości boków tego trójkąta.

Wskazówka:

Rozwiązanie:

Kątem o największej mierze w tym trójkącie jest kąt prosty, więc ciąg $(\alpha, \beta, 90^{\circ})$ jest ciągiem arytmetycznym. Stąd $\beta = \frac{\alpha + 90^{\circ}}{2}$. Ponadto $\alpha = 90^{\circ} - \beta$.

Wobec tego $\beta = \frac{180^{\circ} - \beta}{2}$, a więc $\beta = 60^{\circ}$, czyli $\alpha = 30^{\circ}$.

Teraz przez $a$ i $b$ oznaczmy długości przyprostokątnych, leżące naprzeciw kątów $α$ i $β$ odpowiednio, a przez $c$ długość przeciwprostokątnej.

Wiemy, że $a + b + c = 1 + \sqrt{3}$, a ponadto $a = c\cdot \sin(\alpha) = \frac{c}{2}$ oraz $b = c\cdot \sin(\beta) = \frac{c\sqrt{3}}{2}$.

Stąd $a + b + c = c(\frac{1}{2} + \frac{\sqrt{3}}{2} + 1) = c(\frac{3 + \sqrt{3}}{2}) = \frac{c\sqrt{3}}{2}(1 + \sqrt{3})$. Wobec tego $c = \frac{2\sqrt{3}}{3}$, $a = \frac{\sqrt{3}}{3}$ i $b = 1$ .

Zadanie 15.

Niech $a$ , $b$ , $c$ oznaczają boki pewnego trójkąta, natomiast $h$ - jego wysokość opuszczoną na bok $a$ . Ciąg $(a, b, c, h)$ jest ciągiem geometrycznym. Wykazać, że ten trójkąt jest prostokątny.

Wskazówka:

Rozwiązanie:

(*) Dowód: oznaczmy przez $h c$ wysokość spuszczoną z wierzchołka, w którym sąsiadują boki $a$ i $b$ na bok $c$ . Wówczas $2P = c\cdot h_c$, czyli $h c = b$ . A to oznacza, że bok $b$ jest tym samym, co wysokość spuszczona na bok $c$ , czyli znajduje się pod kątem prostym do boku $c$ .

Zadanie 16.

Ciąg $(a_1,\ldots,a_n)$ jest ciągiem geometrycznym o ilorazie $q$ . Wyznaczyć sumę $T_n= a_1 + 2a_2 + 3a_3 + \ldots + na_n$ w zależności od $a 1$ i $q$ .

Wskazówka 1:

Wskazówka 2:

Rozwiązanie:

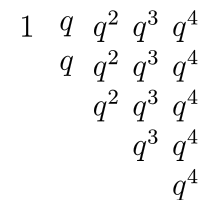
Możemy wypisać sumowane wyrazy jak na rysunku:

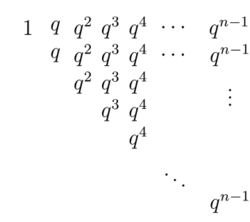
Kolejne rzędy to ciągi geometryczne o ilorazie $q$ , zaczynające się od $q k$ dla $0 \leq k \leq n-1$, a kończące na $q n - 1$ . Suma wyrazów w rzędzie zaczynającym się od $q k$ jest równa $q^k+\ldots + q^{n-1} = q^k(1+q+\ldots + q^{n-k-1}) = q^k \frac{q^{n-k}-1}{q-1} = \frac{q^n-q^k}{q-1}$.

Wobec tego $T_n = \sum_{k=0}^{n-1} \frac{q^n-q^k}{q-1} = \frac{nq^n}{q-1} - \frac{1}{q-1}\sum_{k=0}^{n-1} q^k = \frac{nq^n}{q-1} - \frac{q^n-1}{(q-1)^2}$.

Mnożąc otrzymany wzór przez liczbę $c$ , otrzymujemy $T n$ dla ciągu geometrycznego o ilorazie $q$ i $a 1 = c$ .

Zadanie 17.

Liczby $a$ , $b$ i $c$ są dodatnie, a ich kwadraty tworzą ciąg arytmetyczny. Wykazać, że liczby $x_1 = \frac{1}{b+c}$, $x_2 = \frac{1}{c+a}$, $x_3 = \frac{1}{a+b}$ również tworzą ciąg arytmetyczny.

Wskazówka:

Rozwiązanie:

Wiemy, że liczby $a 2$ , $b 2$ i $c 2$ tworzą ciąg arytmetyczny. Stąd $b 2 - a 2 = c 2 - b 2$ , więc również $r_1 = \frac{b^2-a^2}{(a+c)(b+c)(a+b)} = \frac{c^2-b^2}{(a+c)(b+c)(a+b)} = r_2$, co należało udowodnić.

Zadanie 18.

Liczby dodatnie $a$ , $b$ i $c$ tworzą ciąg arytmetyczny. Udowodnić, że liczby $\frac{1}{\sqrt{b}+\sqrt{c}}$, $\frac{1}{\sqrt{c}+\sqrt{a}}$ i $\frac{1}{\sqrt{a}+\sqrt{b}}$ również tworzą ciąg arytmetyczny.

Wskazówka:

Rozwiązanie:

Zadanie 19.

Niech $(a n)$ będzie ciągiem arytmetycznym. Przez $S k$ oznaczmy sumę początkowych $k$ wyrazów ciągu $(a n)$ . Udowodnić, że zachodzi wzór $S 3 n = 3 S 2 n - 3 S n$ .

Wskazówka:

Rozwiązanie:

$3S_{2n} - 3S_n = 3(\frac{2n(a_1 + a_{2n})}{2} - \frac{n(a_1+a_n)}{2}) = \frac{3n(a_1 + 2a_{2n} - a_n)}{2}$.

Ponieważ ciąg $a n$ jest arytmetyczny, to $a 3 n - a 2 n = a 2 n - a n$ , więc $2 a 2 n - a n = a 3 n$ . Wobec tego powyższe wyrażenie jest równe $\frac{3n(a_1 + a_{3n})}{2} = S_{3n}$.

Jakie inne ciekawe zależności spełniają liczby $S n$ ?

Zadanie 20.

Ciąg $(a n)$ jest zdefiniowany następująco: $a 1$ jest wybraną liczbą z przedziału $(0,1)$ , a dla $n > 1$ wyrazy ciągu są określone przez zależność $(1-a_{n-1})a_n = \frac{1}{4}$. Ponadto załóżmy, że $a 1$ jest wybrane tak, że wszystkie wyrazy ciągu spełniają nierówności $0 < a n < 1$ . Udowodnić, że każdy otrzymany w ten sposób ciąg jest monotoniczny.

Wskazówka:

Rozwiązanie:

Spróbujmy wykazać, że ciąg $a n$ jest niemalejący. Chcemy udowodnić nierówność $a_{n-1} \leq a_n = \frac{1}{4(1-a_{n-1})}$. Ponieważ wyrazy ciągu są dodatnie, ta nierówność jest równoważna $4a_{n-1}(1-a_n-1) - 1 \leq 0$, czyli $4a_{n-1}^2 - 4a_{n-1} + 1 \geq 0$.

Ponieważ $4x^2 - 4x+1 = (2x-1)^2 \geq 0$ dla dowolnej liczby rzeczywistej $x$ , to powyższa nierówność jest spełniona dla dowolnych wartości wyrazów ciągu, więc ciąg $(a n)$ jest niemalejący, niezależnie od wyboru $a 1$ (spełniającego warunki zadania).

Natomiast równość zachodzi, gdy $x = \frac{1}{2}$ - dla $a_1 = \frac{1}{2}$ otrzymujemy ciąg stały.

Zadanie 21.

Ciąg $(a n)$ jest zdefiniowany wzorem $a n = 3 p 2 n + p n - 7 p$ , gdzie $p$ jest pewną liczbą rzeczywistą.

(a) Wykazać, że ciąg $(a n)$ jest arytmetyczny. Obliczyć różnicę tego ciągu w zależności od parametru $p$ .

(b) Dla jakich wartości $p$ ciąg $(a n)$ jest ściśle rosnący? Dla jakich jest ściśle malejący? Ile jest różnych wartości $p$ , dla których ten ciąg jest stały?

Wskazówka:

(b) Dla jakich $p$ różnica ciągu $(a n)$ jest dodatnia (ujemna, zerowa)?

Rozwiązanie:

(b) Ciąg arytmetyczny jest ściśle rosnący wtedy i tylko wtedy, gdy jego różnica jest dodatnia, malejący wtedy i tylko wtedy, gdy różnica jest ujemna, a stały dla $r = 0$ . Wobec tego wystarczy rozwiązać nierówność $r \geq 0$, czyli $p(3p+1) \geq 0$. Otrzymujemy, że $r = 0$ dla dwóch wartości parametru $p$ : 0 i $-\frac{1}{3}$; dla $p$ z przedziału $(-\frac{1}{3},0)$ różnica jest ujemna, czyli ciąg jest ściśle malejący, natomiast dla $p$ z półprostych $(-\infty,-\frac{1}{3})$ i $(0, \infty)$ różnica jest dodatnia, czyli ciąg jest ściśle rosnący.

Zadanie 22.

O ciągu $(a n)$ wiadomo, że dla każdego $n \geq 1$ suma $n$ pierwszych wyrazów jest równa $S_n = n + \frac{1}{n}$. Wyznaczyć wzór określający $a n$ .

Wskazówka:

Rozwiązanie:

Ponieważ $S_n = a_1 + a_2 + \ldots + a_{n-1} + a_n = S_{n-1} + a_n$, to $a_n = S_n - S_{n-1} = n + \frac{1}{n} - (n-1) - \frac{1}{n-1} = 1 + \frac{n-1 - n}{n(n-1)} = 1 - \frac{1}{n(n-1)} = \frac{n^2-n-1}{n^2-n}$.

Zadanie 23.

Dany jest ciąg arytmetyczny $(a n)$ . Wyznaczyć wzór na sumę wyrazów tego ciągu o indeksach podzielnych przez pewną liczbę całkowitą $m$ , nie większych niż $k m$ : $\sum_{i=1}^{m}a_{im}$ (w zależności od $a 1$ i różnicy $r$ ).

Wskazówka:

Rozwiązanie:

Wobec tego, licząc sumę $k$ pierwszych wyrazów tego ciągu, możemy skorzystać z wzoru $S_k(b_n) = k\frac{b_1 + b_k}{2}$. Stąd $S_k(b_n) = k\frac{a_m + a_{km}}{2} = k\frac{a_1 + (m-1)r + a_1 + (km-1)r}{2} = k(a_1 + \frac{(km + m -2)r}{2})$.

Zadanie 24.

Dla ciągu arytmetycznego $(a n)$ , dla każdego $n \in \mathbb{N}$ zachodzi $S n = 3 n 2 - 7 n + 2$ . Wyznaczyć wartość wyrażenia $a_3 + a_6 + a_9 + \ldots + a_{3n}$ dla dowolnej liczby naturalnej $n$ .

Wskazówka:

Rozwiązanie:

Określmy ciąg $(b n)$ , biorąc do niego co trzeci wyraz ciągu $(a n)$ , czyli $b n = a 3 n$ . Wówczas naszym zadaniem jest obliczenie sumy $n$ początkowych wyrazów ciągu $(b n)$ . Możemy wyprowadzić wzór ogólny na wyrazy ciągu $(b n)$ : $b_n = a_{3n} = 6\cdot 3n - 10 = 18n-10$.

Zauważmy, że $b_n - b_{n-1} = 6\cdot 3n - 10 - 6\cdot 3(n-1) + 10 = 18$. Różnica sąsiednich wyrazów ciągu $b n$ jest stała - jest to ciąg arytmetyczny. Możemy więc łatwo obliczyć sumę jego $n$ początkowych wyrazów ze wzoru $S_n(b_n) = n\frac{b_1 + b_n}{2} = \frac{n(8 + 18n-10)}{2} = 9n^2 - n$ (lub skorzystać z zadania 23).

Zadanie 25.

Ciąg $(a n)$ jest zdefiniowany wzorem $a_n = \sqrt{n} + \frac{396}{\sqrt{n}}$. Ile wyrazów tego ciągu jest mniejszych od $45$ ?

Wskazówka:

Rozwiązanie:

Podstawmy $x = \sqrt{n}$ - wówczas rozwiązywana nierówność ma postać $x 2 - 45 x + 396 < 0$ . Żeby znaleźć rozwiązania, liczymy $\Delta = 45^2 - 4\cdot 396 = 2025 - 1584 = 441$, a stąd $\sqrt{\Delta} = 21$. Wobec tego pierwiastkami równania $x 2 - 45 x + 396 = 0$ są $x_1 = \frac{45 - 21}{2} = 12$ i $x_2 = \frac{45+21}{2}=33$. Natomiast badana nierówność jest spełniona dla wszystkich $x$ z przedziału $(x 1, x 2)$ .

Chcielibyśmy stąd uzyskać informację, jakie liczby naturalne $n$ spełniają wyjściową nierówność. Ponieważ $n = x 2$ i $x < x 2$ , to musi być spełniony warunek $n < x_2^2$. Analogicznie otrzymujemy warunek $n > x_1^2$. Wyraz $a n$ jest mniejszy niż 45 wtedy i tylko wtedy, gdy $n$ spełnia obie te nierówności: $122 = 144 < n < 33 3 = 1089$ . Wobec tego w ciągu $(a n)$ są $1088 - 144 = 944$ wyrazy mniejsze od 45.

Zadanie 26.

Dany jest ciąg $(a n)$ zdefiniowany wzorem $a_n = \sqrt{n^2 - 7n + 5}$. Czy ciąg $(a n)$ jest monotoniczny? Czy jest monotoniczny od pewnego miejsca?

Wskazówka:

Rozwiązanie:

Funkcja kwadratowa $f (x) = x 2 - 7 x + 5$ przyjmuje najmniejszą wartość w punkcie $x_0 = \frac{7}{2}$, przed punktem $x 0$ maleje, a za nim rośnie. Ciąg $(b n)$ powstaje przez obcięcie funkcji $f$ do zbioru liczb naturalnych, wobec tego jest malejący dla $1 \leq n < \frac{7}{2}$, a dla $n > \frac{7}{2}$ jest rosnący. To oznacza, że ciąg $(b n)$ jako całość nie jest monotoniczny (więc ciąg $(a n)$ również).

Ale jeśli zapomnimy o trzech pierwszych wyrazach, definiując podciąg $c n = b n + 3$ , to oczywiście otrzymany ciąg $(c n)$ będzie ściśle rosnący. Możemy powiedzieć, że ciąg $(b n)$ jest monotoniczny począwszy od $n \geq 4$. To samo odnosi się do ciągu $(a n)$ .

Ciągi - zadania

dla autorów