Pojęcie funkcji to zapewne najważniejsze pojęcie matematyki. W poniższym tekście spojrzymy na nie z pewnej odpowiednio dobranej perspektywy, koncentrując naszą uwagę na wykresach funkcji, których zarówno dziedziną jak i zbiorem wartości jest zbiór liczb rzeczywistych. Jest to bardzo ważna, choć - przyznajmy - nieco wybiórcza perspektywa. Naszym celem nie jest jednak zastępowanie podręczników, ale ich wzbogacenie w miarę rozbudowanym opisem zagadnienia z ustalonego punktu widzenia.
Plan naszego działania jest następujący:
- w pierwszej części naszych rozważań zajmiemy się przeglądem podstawowych własności funkcji;
- w drugiej części przyjrzymy się przekształceniom płaszczyzny, które z jednych wykresów funkcji potrafią wyprodukować wykresy innych funkcji;
- w części trzeciej zastosujemy wiedzę z poprzednich części do trzech najprostszych funkcji, uzyskując całkiem bogatą teorię.
Ale po kolei. Na początek - definicja.
|
Definicja 1.1. Funkcją ze zbioru A w zbiór B nazywamy przyporządkowanie każdemu elementowi ze zbioru A dokładnie jednego elementu zbioru B. Zbiór A nazywamy dziedziną funkcji, a elementy zbioru A - argumentami funkcji. Każdy element zbioru B, który został przyporządkowany pewnemu argumentowi, nazywamy wartością funkcji.
|
Schematyczny obrazek, jaki towarzyszy zwykle definicji funkcji, może wyglądać na przykład tak:
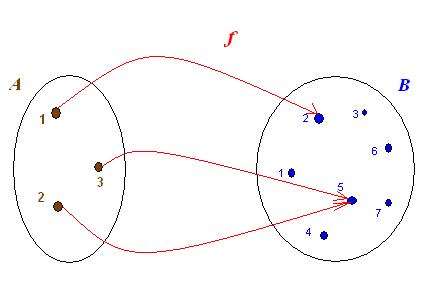
Dziedzina funkcji f to zbiór A:
Zbiór wartości W to podzbiór zbioru B złożony z liczb 2 oraz 5:
Strzałki na rysunku obrazują przyporządkowanie. Widzimy, że liczbie 1 funkcja f przypisuje liczbę 2, co zapisujemy następująco:
Z kolei argumentom 2 oraz 3 została przypisana ta sama wartość funkcji równa 5:
Uwaga 1.2. Funkcja f jest zdefiniowana wtedy, gdy jasno został określony sposób, w jaki danemu argumentowi x przyporządkowana jest odpowiadająca mu wartość funkcji: f(x). Znajdowanie f(x), gdy dany jest argument x, nazywamy obliczaniem wartości funkcji.
Uwaga 1.3. Dziedzina funkcji bywa czasami bezpośrednio podawana w definicji. Jeśli nie jest podana, przyjmujemy, że jest nią zbiór wszystkich tych liczb, dla których wzór funkcji ma sens. (Wyrażenie "dany wzór ma sens dla liczby x", oznacza po prostu, że dany wzór z danej liczby rzeczywistej x "potrafi wyprodukować" pewną jednoznacznie ustaloną liczbę rzeczywistą).
Przykład 1.4. Określimy funkcję f następująco:
Jej dziedziną jest zbiór liczb rzeczywistych, bo dla każdej liczby rzeczywistej x, możemy w jednoznaczny sposób wyznaczyć kwadrat liczby x, np:
Przykład 1.5. Określimy funkcję f następująco:
f(x) = M wtedy i tylko wtedy, gdy M jest częścią całkowitą liczby x, to znaczy gdy:
- M jest liczbą całkowitą, a ponadto:
- spełniona jest nierówność: \(M\leq x <M+1 \).
Zauważmy, że dla każdej liczby rzeczywistej x jesteśmy w stanie ustalić - w sposób jednoznaczny - wartość funkcji f(x). Przykładowo:
- \( f\left(8,023644\right)=8\), bowiem \(8\leq 8,023644 <9\)
- \(f\left(\pi\right)=3\), bowiem \(3\leq \pi <4\)
- \(f\left(-0,12\right)=-1\), bowiem \(-1\leq 0,12 <0\)
- \(f\left(-\pi\right)=-4\), bowiem \(-4\leq \pi <3\)
Dziedziną funkcji f jest więc zbiór liczb rzeczywistych. Wartościami funkcji f są z kolei wszystkie liczby całkowite.
Uwaga 1.6. W poniższym tekście będziemy stosować specjalne oznaczenie dla funkcji f określonej w przykładzie 1.5. Mianowicie przez [x] będziemy odtąd oznaczać część całkowitą liczby x.
Zazwyczaj przyjmujemy, że daną funkcję rozumiemy dość dobrze, gdy uda nam się ustalić:
- jej miejsca zerowe;
- przedziały, na których funkcja rośnie i te, na których maleje;
- największe i najmniejsze wartości, jaka dana funkcja osiąga na wybranych przedziałach.
Mając taką wiedzę i pewne dodatkowe informacje, w wielu przypadkach jesteśmy już w stanie naszkicować wykres funkcji, który w pewnym sensie najlepiej obrazuje daną funkcję. Dlatego zanim zajmiemy się samymi wykresami, przyjrzymy się bliżej wymienionym wyżej własnościom funkcji. Najpierw musimy je ściśle zdefiniować.
|
Definicja 1.7. Argument z nazywamy miejscem zerowym funkcji f, jeśli:
|
Przykład 1.8. Miejscem zerowym funkcji f(x) = 2x + 4 jest liczba z = − 2, gdyż:
|
Definicja 1.9. Mówimy, że funkcja f jest rosnąca na zbiorze A, jeśli dla każdych x oraz y należących do zbioru A mamy spełnioną implikację:
Funkcja f jest ściśle rosnąca, jeśli dla każdych x oraz y należących do zbioru A mamy spełnioną implikację:
|
Analogicznie definiujemy funkcje malejące i ściśle malejące.
|
Definicja 1.10. Mówimy, że funkcja f jest malejąca na zbiorze A, jeśli dla każdych x oraz y należących do A mamy spełnioną implikację:
Funkcja f jest ściśle malejąca, jeśli dla każdych x oraz y należących do A mamy spełnioną implikację:
|
Specjalną nazwą wyróżniamy też funkcje, które przyjmują tylko jedną wartość.
|
Definicja 1.11. Mówimy, że funkcja f jest stała na zbiorze A, jeśli dla pewnej ustalonej liczby c mamy f(x) = c dla każdego argumentu \(x \in A\) .
|
Przykład 1.12.
- Funkcja f(x) = 6x jest ściśle rosnąca (na całej swojej dziedzinie), bowiem jeśli x < y, to po pomnożeniu obu stron przez 6, otrzymujemy 6x < 6y, czyli f(x) < f(y).
- Funkcja f(x) = − 1 jest stała.
- Funkcja f(x) = − x jest ściśle malejąca, gdyż jeśli x<y, to mnożąc obie strony przez -1 dostajemy -x>-y, czyli f(x)>f(y).
Funkcje ściśle rosnące i ściśle malejące to przykłady funkcji różnowartościowych.
|
Definicja 1.13. Funkcja f jest różnowartościowa, jeśli z tego, że f(x) = f(y) wynika, że x = y .
|
Przykład 1.14. Funkcja f(x) = 2x jest różnowartościowa, gdyż jeśli 2x = 2y to po podzieleniu obu stron przez 2 dostaniemy x = y. A zatem z tego, że f(x) = f(y) wynika, iż x = y.
Gdy mamy do czynienia z funkcją różnowartościową f, to możemy zdefiniować nową funkcję "odwracając strzałki" w przyporządkowaniu określonym przez f, to znaczy przypisując wartościom f odpowiadające im argumenty.
|
Definicja 1.15. Niech f będzie funkcją różnowartościową o dziedzinie A i zbiorze wartości W. Funkcją odwrotną do funkcji f nazywamy funkcję f − 1 określoną na zbiorze W i zdefiniowaną dla każdego x należącego do W następująco: f − 1(y) = x wtedy i tylko wtedy, gdy f(x) = y.
|
Przykład 1.16. Funkcja f jest opisana następującym grafem:
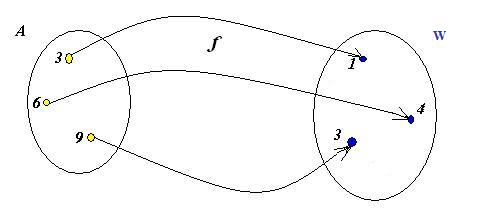
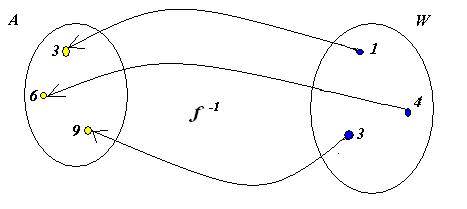
Graf jej funkcji odwrotnej uzyskujemy, odwracając strzałki i pozbywając się tych elementów, które nie są wartościami funkcji f.
Zadanie 1.1.: Oblicz wartość funkcji f dla argumentu \(x=\frac{39}{7}\), gdy funkcja f dana jest wzorem:
a. \(f(x)=x-\left [x \right],\)
b. \(f(x)=\frac{1}{x}-\left [\frac{1}{x}\right ],\)
przy czym symbol [x] oznacza część całkowitą liczby x.
Rozwiązanie
a. Dzieląc 39 przez 7, nietrudno spostrzec, że \(\frac{39}{7}=5\frac{4}{7}\). Następnie obliczamy:
\(f\left(\frac{39}{7}\right)=\frac{39}{7}-\left [\frac{39}{7}\right]=5\frac{4}{7}-\left[5\frac{4}{7}\right]=5\frac{4}{7}-5=\frac47\).
b. Mamy: \(f\left (\frac{39}{7} \right)=\frac{7}{39}-\left [\frac{7}{39}\right]=\frac{7}{39}-0=\frac{7}{39}\)
Zadanie 1.2. Dziedziną funkcji f jest zbiór liczb naturalnych (czyli mamy tu do czynienia po prostu z ciągiem). Oblicz f(5), gdy funkcja f jest określona następująco:
a. dla n=1 mamy: \(f\left (1\right)=1\), natomiast dla n>1 zachodzi równość: \(f(n)=(n-1)\cdot f(n)\).
b. dla n=1 mamy: \(f\left(1\right)=1\), natomiast dla n>1 zachodzi równość: \(f(n)=1+\frac{1}{1+f(n-1)}\).
Wskazówka. Najpierw należy obliczyć f(2), f(3) i f(4).
Rozwiązanie
a. Mamy:
- \(f(2)=2\cdot1=2\),
- \(f(3)=3\cdot f(2)=3\cdot2=6\),
- \(f(4)=4\cdot f(3)=4\cdot6=24\).
A zatem:
- \(f(5)=5\cdot f(4)=5\cdot24=120.\)
Zauważmy, że funkcję f można też określić wzorem:
- \(f(n)=1\cdot2\cdot ... \cdot n=n!\)
b. Mamy:
- \(f(2)=1+\frac1{1+f(1)}=1+\frac{1}{1+1}=\frac32,\)
- \(f(3)=1+\frac1{1+f(2)}=1+\frac{1}{\frac52}=\frac75\),
- \(f(4)=1+\frac1{1+f(3)}=1+\frac{1}{1+\frac75}=\frac{17}{12}\).
A zatem:
- \(f(5)=1+\frac1{1+f(4)}=1+\frac{1}{1+\frac{17}{12}}=\frac{41}{29}\).
Zadanie 1.3. Określ dziedzinę funkcji f danej wzorem:
a. \(f(x)=\frac{1}{x^2+5x}\),
b. \(f(x)=\sqrt{x^2-9}+\sqrt{16-x^2}\).
Rozwiązanie:
a. Mianownik musi być różny od zera. Zauważmy, że: \(x^2+5x=x\left(x+5\right)\).
Ponieważ iloczyn dwóch liczb jest zerem wtedy i tylko wtedy, gdy przynajmniej jedna z nich jest zerem, więc w mianowniku nie może stać ani zero, ani minus pięć.
Stąd dziedzina funkcji to zbiór: \( D=\mathbb{R}\setminus\{-5,0\}\)
b. Musimy mieć jednocześnie: \(x^2\geq 9\) a także: \(16\geq x^2\).
Stąd \(x\in(-\infty;-3]\cup [3;\infty)\) i jednocześnie: \(x\in [-4;4]\).
A zatem dziedziną funkcji jest zbiór: \(D = [-4;-3]\cup[3;4]\).
Zadanie 1.4. Dziedziną funkcji G jest przedział (0;1], na którym określona jest ona wzorem: \(G(x)=\frac{1}{x}-\left[\frac{1}{x}\right]\)
Wykaż, że funkcja G ma nieskończenie wiele miejsc zerowych.
Rozwiązanie:
Do tego, by argument x był miejscem zerowym funkcji G musimy mieć: \(\frac1x=\left [\frac1x\right ]\), tzn. odwrotność liczby x musi być liczbą całkowitą. W dodatku, skoro x jest dodatnie, więc jest to liczba całkowita dodatnia.
A zatem miejsca zerowe f to liczby: \(1,\frac12, \frac13, \frac14,...\). Jest ich nieskończenie wiele.
Zadanie 1.5. Znajdź zbiór wartości funkcji:
a. f(x) = [x]
b. f(x) = x − [x].
Rozwiązanie:
a. Zauważmy, że: \(f\left(z\right)=[z]=z\) dla każdej liczby całkowitej. A zatem każda liczba całkowita jest wartością funkcji. Ponadto, wartość funkcji musi być liczbą całkowitą.
A zatem zbiór wartości funkcji f to zbiór liczb całkowitych: \( W = \mathbb{Z}\).
b. Dla x z przedziału [0;1) mamy: \(f\left(x\right)=x-0=x\). A zatem każda liczba z wymienionego przedziału jest wartością funkcji.
Żadna inna być nie może, bo \(0\leq f(x)<1\).
Zbiór wartości funkcji f to zatem przedział: [0;1).
Zadanie 1.6. Znajdź najmniejszą wartość funkcji: \(f(x)=x^2+\frac{1}{x^2}\).
Wskazówka
Można skorzystać z nierówności: \((x^2-1)^2=x^4-2x^2+1\geq0\).
Rozwiązanie: Dzieląc nierówność ze wskazówki przez x2, otrzymujemy: \(x^2+\frac{1}{x^2}\geq2.\)
Stąd: \(f(x)\geq 2\).
Mamy też: f(1)=2. Stąd najmniejsza wartość, jaką przyjmuje funkcja f to liczba 2.
Zadanie 1.7. Znajdź największą wartość funkcji: \(f(x)=\frac1{1+x^2}\)
Rozwiązanie:
Ponieważ \(x^2+1\geq 1\),
więc \(f(x)\leq 1\).
Ponadto f(0)=1. A zatem największa wartość funkcji f to liczba 1.
Zadanie 1.8. Wykaż, że funkcja \(f(x)=\left [x\right]\)
jest rosnąca, ale nie jest ściśle rosnąca.
Rozwiązanie:
Załóżmy, że: \(x_1\leq x_2\).
Wtedy każda liczba całkowita, która nie jest większa od x1, nie jest też większa od x2, więc \([x_1]\leq[x_2]\).
A zatem mamy wtedy \(f(x_1)\leq f(x_2)\).
Funkcja f nie jest jednak ściśle rosnąca, gdyż na przykład \(f\left(\frac15\right)=f\left(\frac14\right)\), chociaż \(\frac15<\frac14\).
Zadanie 1.9.* Niech dana będzie pewna liczba rzeczywista M. Określamy teraz funkcję f, której dziedziną są dodatnie liczby całkowite, w następujący sposób:
a. f(1)=M, a ponadto
b. dla każdego naturalnego n>0 zachodzi równość \(f(n+1)=1+\frac{1}{2+\frac{1}{f(n)}}\).
Wykaż, że funkcja f jest
a. rosnąca, gdy M=1;
b. malejąca, gdy M=2.
Rozwiązanie:
a. Bezpośrednio sprawdzamy, że \(f(1) = 1 < \frac 43 = f(2)\).
Załóżmy teraz, że \(0< f\left(n\right)\leq f(n+1)\), dla pewnego n>0.
Wtedy \(\frac{1}{f(n)}\geq \frac{1}{f(n+1)}\),
a w konsekwencji: \(2+\frac{1}{f(n)}\geq 2+\frac{1}{f(n+1)}\).
Oba wyrażenia są dodatnie, a zatem porównując ich odwrotności znów zmieniamy znak i mamy \(\frac{1}{2+\frac{1}{f(n)}}\leq \frac1{2+\frac{1}{f(n+1}}\).
Wystarczy teraz do obu stron nierówności dodać liczbę 1, by otrzymać \(f\left(n+1\right)\leq f(n+2)\).
Wynika stąd, że wartości funkcji możemy uszeregować następująco \(f(1)\leq f(2)\leq f(3)\leq f(4)\leq ...\)
A zatem f - jako funkcja określona na zbiorze liczb naturalnych jest rosnąca.
b. Rozumowanie jest w pełni analogiczne do punktu a, z tym, że tym razem mamy \(f\left(1\right) = 2 > \frac{7}{5} = f(2)\).
W konsekwencji zakładamy, że \(f\left(n\right)>f(n+1)\)
i udowadniamy potem, że \(f\left(n+1\right)>f(n+2)\).
Zadanie 1.10. Wykaż, że funkcja \(f(x)=1+\frac{1}{2+x}\)
jest malejąca na przedziale \((-2;\infty)\).
Rozwiązanie: Niech \(-2<x_1\leq x_2\). Wtedy \(0<x_1+2\leq x_2+2\).
Stąd \(\frac1{x_1+2}\geq\frac1{x_2+2}\).
Dodajemy do obu stron liczbę 1 i dostajemy \(f\left(x_1\right)\geq f(x_2)\).
Zadanie 1.11. Wykaż, że funkcja f(x) = 2 + 3x jest różnowartościowa, a następnie znajdź funkcję do niej odwrotną.
Rozwiązanie:
Jeśli 2 + 3x1 = 2 + 3x2,
to odejmując od obu stron 2 mamy 3x1 = 3x2
i po podzieleniu obu stron przez 3: x1 = x2. Czyli f jest różnowartościowa.
Niech teraz y=f(x), czyli: y = 2+3x. Wtedy: y-2=3x, skąd \(x=\frac{y-2}{3}\).
W takim razie funkcja f − 1, odwrotna do f dana jest wzorem \(f(y)=\frac{y-2}{3}\)
Zadanie 1.12.** Funkcja f spełnia dla każdej liczby rzeczywistej x równość \(f\left(x\right)+2f(-x)=-2x+3\).
Oblicz f(3).
Wskazówka
Skorzystaj z podanej własności f dla x = 3 oraz x = − 3.
Rozwiązanie:
Mamy \(f\left(3\right)+2f(-3)=-2\cdot 3+3=-3\),
czyli \(f\left(3\right)=-3-2f(-3)\).
Z drugiej strony \(f\left(-3\right)+2f(3)=-2 \cdot (-3)-3=-9\),
czyli \(f\left(-3\right)=-9-2f(3)\).
Łącząc te dwie obserwacje otrzymujemy \(f\left(3\right)=-3-2[-9-2f(3)],\)
czyli \(f\left(3\right)=15+4f(3)\).
Stąd f(3) = − 5.
Zadanie 1.13.* Funkcja f spełnia dla każdych liczb rzeczywistych x oraz y zależność \(f(xy)=x\cdot f(y+1)\).
Oblicz f(11).
Wskazówka
Wykaż, że \(f\left(n\right)=f(n+1)\) dla dowolnej liczby naturalnej n. Dla jakiego n łatwo jest obliczyć wartość funkcji?
Rozwiązanie:
Niech x = 1 oraz y = n. Wtedy \(f(n)=f(1\cdot n)=1\cdot f(n+1)=f(n+1)\).
Stąd łatwo wynika, że: f(n) = f(0) dla dowolnej naturalnej liczby n.
Z drugiej strony \(f\left(0\right)=f(0\cdot 1)=0\cdot f(1)=0\).
A zatem f(11) = 0.
Zadanie 1.14.* Funkcja f spełnia warunki \(f(xy)= f\left(x\right)+f(y)\) oraz f(2) = 1.
Oblicz f(16).
Wskazówka Najpierw oblicz f(4).
Rozwiązanie:
Mamy:
- \(f(4)=f(2\cdot2)=f(2)+f(2)=2\),
- \(f(16)=f(4\cdot4)=f(4)+f(4)=2+2=4\).
Zadanie 1.15.* Wiadomo, że dla funkcji f spełniona jest zależność:
\(f\left(\frac{x}{x+1}\right)=x\)
dla dowolnego \(x\neq -1\). Oblicz f(2).
Wskazówka Przedstaw liczbę 2 w odpowiedniej postaci.
Rozwiązanie:
Zauważmy, że jeśli \(2=\frac{x}{x+1}\),
to 2x+2=x, czyli x=-2.
Stąd \(f(2)=f\left (\frac{-2}{-2+1}\right )=-2.\)
