Zajmiemy się teraz obiektem, który będzie odtąd w centrum naszych rozważań: wykresem funkcji. Zacznijmy od dość formalnej definicji, która stanie się bardziej jasna po zobrazowaniu jej w serii rysunków poniżej.
|
Definicja 2.1. Niech A będzie zbiorem liczb rzeczywistych lub pewnym niepustym podzbiorem tego zbioru. Wykresem funkcji \(f: A \rightarrow \mathbb{R}\) nazywamy zbiór punktów płaszczyny W określony następująco: \(W=\left\{ (x,y): x\in A\;\;oraz\;\; y=f(x)\right\}\)
|
Wykresy funkcji są bardzo ważne, bo pozwalają w prosty graficzny sposób przedstawiać najważniejsze własności funkcji:
1) Aby odczytać z wykresu wartość funkcji f dla danego argumentu x=a, należy przez punkt na osi OX oznaczony a (czyli o współrzędnych (a;0)) poprowadzić pionową prostą aż do zetknięcia się z wykresem funkcji f, a następnie od punktu zetknięcia poziomą prostą do zetknięcia z osią OY. Punkt przecięcia z osią OY ma drugą współrzędną równą f(a).
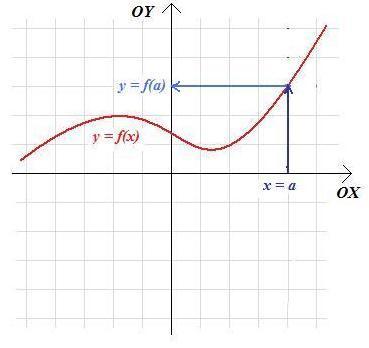
2) Aby zobaczyć na wykresie funkcji f, dla jakich argumentów x przyjmuje ona wartość c należy wykreślić poziomą prostą przechodzącą przez punkt (0;y), czyli prostą o równaniu y=c, i odczytać iksowe współrzędne wszystkich punktów przecięcia wykresu z prostą
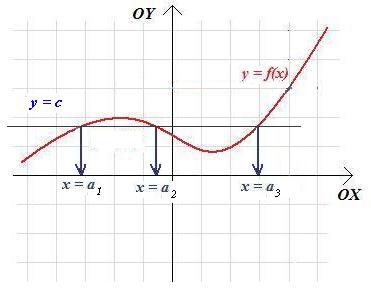
3) Aby znaleźć na wykresie przedziały, na których funkcja rośnie należy wyznaczyć te przedziały, na których wykres funkcji wznosi się do góry, gdy poruszamy się w kierunku strzałki osi OX. Przedziały, na których funkcja maleje, to z kolei te przedziały, na których wykres funkcji opada.
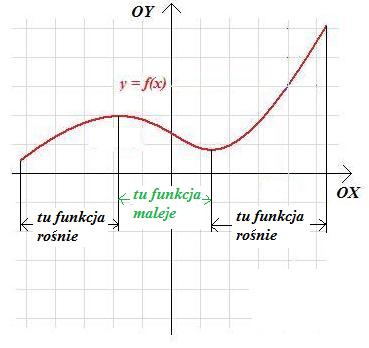
Jak widzimy, mając wykres funkcji, potrafimy w wielu wypadkach określić dużo własności funkcji bez większego wysiłku. Dlatego wykresy funkcji są bardzo ważne.
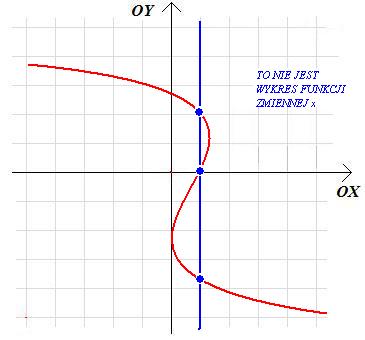
Zauważmy teraz, że charakterystyczną cechą wykresu funkcji zmiennej x jest to, że jego przecięcie z dowolna pionową prostą (czyli prostą o równaniu x=a) ma co najwyżej jeden punkt wspólny:
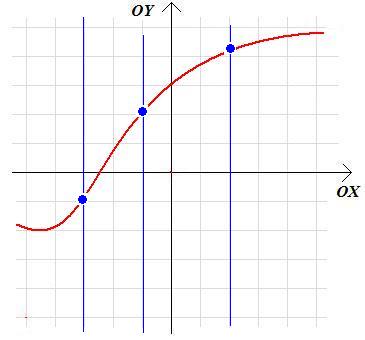
Jeśli krzywa w układzie współrzędnych ma więcej niż jeden punkt przecięcia z jakąkolwiek prostą pionową, to nie może być ona wykresem funkcji zmiennej x:
Spojrzymy teraz na wykres funkcji w układzie współrzędnych jak na pewną figurę geometryczną. Jako figurę geometryczną możemy wykres przekształcać za pomocą rozmaitych izometrii płaszczyzny. Część z nich ma tę miłą własność, że przekształcony wykres jest nadal wykresem pewnej funkcji.
|
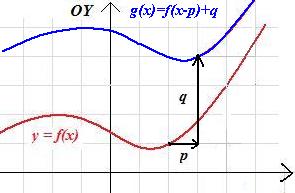
Twierdzenie 2.2. Jeśli wykres funkcji f przesuniemy - o a jednostek w lewo, to otrzymamy wykres funkcji g(x) = f(x + a) - o a jednostek w prawo, to otrzymamy wykres funkcji g(x) = f(x − a) - o b jednostek w górę, to otrzymamy wykres funkcji g(x) = f(x) + b - o b jednostek w dół, to otrzymamy wykres funkcji g(x) = f(x) − b
|
Powyższe twierdzenie możemy ująć krótko:
|
Twierdzenie 2.3. Wykres funkcji f po przesunięciu o wektor [p;q] staje się wykresem funkcji: \(g\left(x\right)=f(x-p)+q \).
|
Kolejne przekształcenia płaszczyzny, które zmieniają wykresy na wykresy, to symetrie względem osi.
|
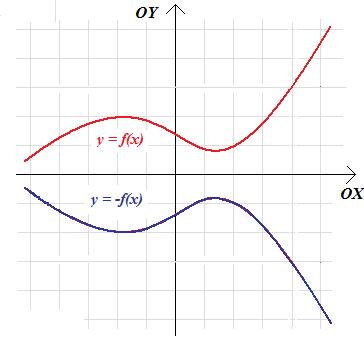
Twierdzenie 2.4. Jeżeli wykres funkcji f odbijemy symetrycznie względem osi OX, to otrzymamy wykres funkcji \(h\left(x\right)= -f(x)\).
|
|
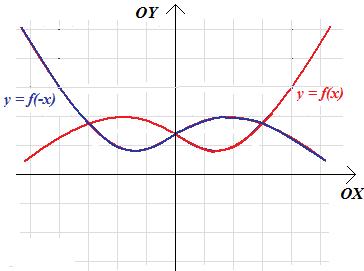
Twierdzenie 2.5. Jeśli wykres funkcji f odbijemy symetrycznie względem osi OY, to otrzymamy wykres funkcji \(g\left(x\right)= f(-x)\).
|
Oprócz symetrii względem prostych pionowych i poziomych, kolejnym przekształceniem, które przekształca wykres danej funkcji na wykres pewnej (być może innej) funkcji jest symetria środkowa.
|
Twierdzenie 2.6. Jeżeli wykres funkcji f odbijemy symetrycznie względem punktu (0;0), to otrzymamy wykres funkcji określonej wzorem: \(k\left (x\right)=-f(-x)\)
|
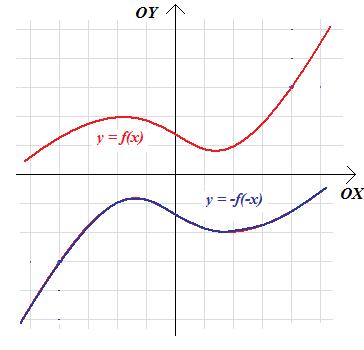
Teza twierdzenia wynika natychmiast z faktu, że symetria środkowa względem punktu (0;0) oznacza dokładnie to samo, co złożenie symetrii względem osi OX i OY (tzn.: ten sam efekt uzyskamy odbijając symetrycznie wykres f najpeirw względem osi - powiedzmy - OX, a potem OY).
|
Twierdzenie 2.7. Jeżeli te częsci wykresu funkcji f, które leżą poniżej osi OX odbijemy symetrycznie względem osi OX, a pozostałe części pozostawimy bez zmian, to otrzymamy wykres funkcji określonej wzorem: \(k\left (x\right)=|f(x)|\)
|
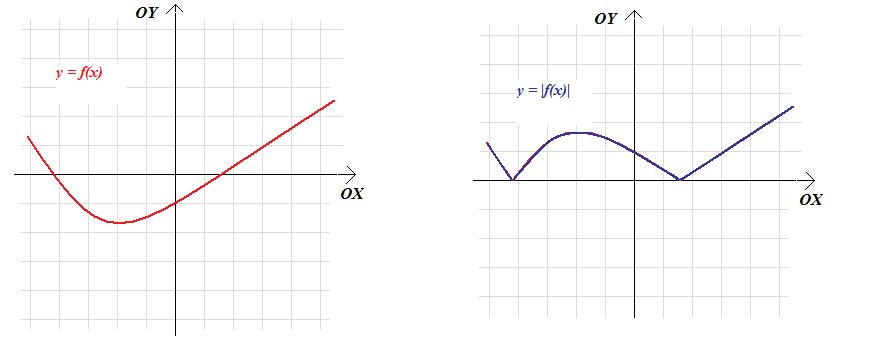
Na koniec rozważań o przekształceniach wykresu funkcji, przyjrzymy się związkowi pomiędzy wykesem funkcji f, a wykresem funkcji g danej wzorem:
\(g(x)=af\left(b \cdot x\right),\)
gdzie a i b to pewne liczby rzeczywiste.
|
Twierdzenie 2.8. Aby z wykresu funkcji f uzyskać wykres funkcji \(g(x)=af\left(x\right)\) należy wykres funkcji f - rozciągnąć a razy w kierunku pionowym, gdy a>1 - ścisnąć \(\frac{1}{a}\) razy wkierunku pionowym, gdy 0<a<1.
|
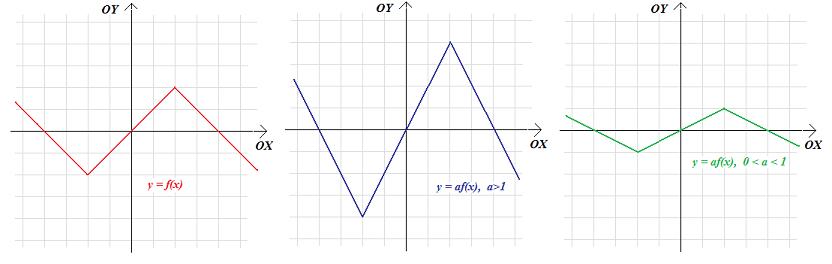
|
Twierdzenie 2.9. Aby z wykresu funkcji f uzyskać wykres funkcji \(g(x)=f\left(bx\right)\) należy wykres funkcji f - ścisnąć b razy w kierunku poziomym, gdy b>1 - rozciągnąć \(\frac{1}{b}\) razy wkierunku poziomym, gdy 0<b<1. |
W poniższych zadaniach będziemy wielokrotnie korzystać z wykresu funkcji:
\(V\left(x\right)=|x|,\)
który wygląda następująco:
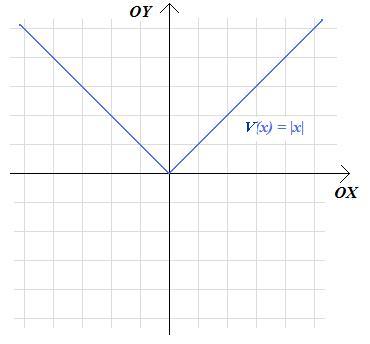
Widzimy, że powyższy wykres (nieco przypominający literę V - ale z tą główną różnicą, że ramiona tego wykresu nigdy się nie kończą) zbudowany jest z dwóch półprostych oraz ich punktu wspólnego, który nazywać będziemy poniżej czubkiem tego wykresu lub kantem tego wykresu.
Zadanie 2.1. Wiedząc, jak wygląda wykres funkcji V(x) = | x | , narysuj wykresy następujących funkcji:
a. \(f\left(x\right)=|x-1|\)
b. \(f\left(x\right)= |x+2|\)
c. \(f\left(x\right)=|x|+3\)
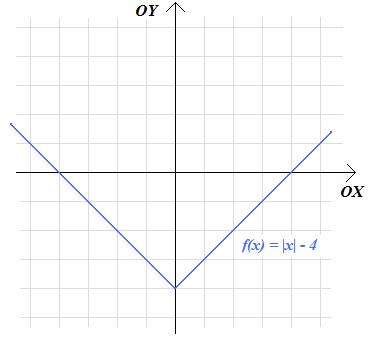
d. \(f\left(x\right)= |x|-4\)
Rozwiązanie. Zgodnie z Twierdzeniem 2.2. w kolejnych przypadkach przesuwamy wykres funkcji V o:
a. jedną jednostkę w prawo;
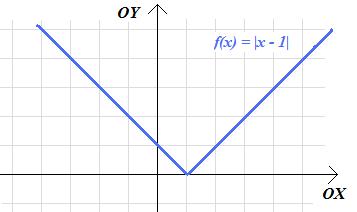
b. dwie jednostki w lewo;
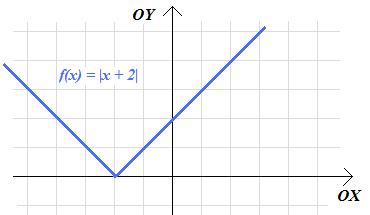
c. trzy jednostki w górę;
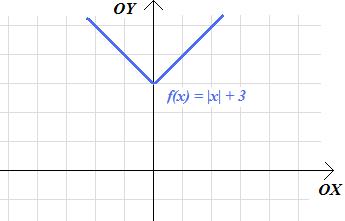
d. cztery jednostki w dół.
Zadanie 2.2. Wiedząc, jak wygląda wykres funkcji V(x)=|x| narysuj wykres funkcji:
a. \(W\left(x\right)=-|x|\) b. \(S\left(x\right)=|-x|\)
Rozwiązanie. W przypadku a. zgodnie z Twierdzeniem 2.4. odbijamy wykres funkcji V względem osi OX i uzyskujemy następujący wykres funkcji W:
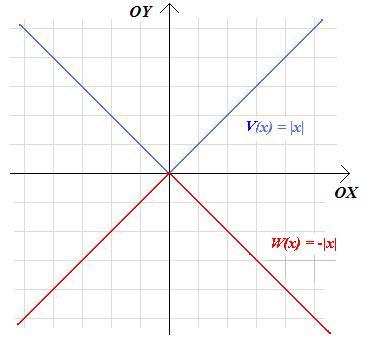
W przypadku b. wykres funkcji S pokrywa się z wykresem funkcji V, gdyż:
\(V\left(x\right)=|x|=|-x|=S(x)\)
Zadanie 2.3. Przesuń wykres funkcji V(x)=|x| o odpowiedni wektor uzyskując wykres funkcji: f(x) = | x − 1 | + 2, a następnie narysuj wykresy funkcji:
a. \(g\left(x\right)= f(-x)\) b. \(h\left(x\right)= -f(x)\)
Rozwiązanie. Zgodnie z Twierdzeniem 2.3. najpierw przesuwamy wykres funkcji V o wektor [1;2].
Następnie w przypadku a. odbijamy otrzymany wykres względem osi OY.
W przypadku b. otrzymany wykres odbijamy względem osi OX.
W rezultacie otrzymujemy następujące wykresy:
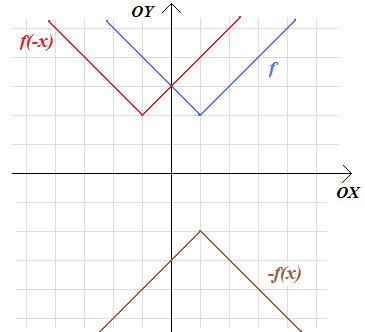
Zadanie 2.4. Funkcja f dana jest wzorem:
\(f\left(x\right)=|x-2|+3\).
Jaki wzór ma funkcja g, której wykresem jest obraz wykresu funkcji f w symetrii względem:
a. osi OX; b. osi OY.
\(g\left(x\right)=-f(x)=-|x-2|-3\)
W przypadku b.:
\(g(x)=f\left(-x\right)=|-x-2|+3=|x+2|+3\)
Zadanie 2.5. Oś OY jest osią symetrii wykresu funkcji f. Wiadomo, że f(2) = 4. Ile jest równe f( − 2)?
\(f\left(-2\right)=4\).
Zadanie 2.6. Oś OX jest osią symetrii wykresu funkcji f określonej dla każdej liczby rzeczywistej. Oblicz:
\(f\left(\sqrt{\pi}+\sqrt{2+\sqrt{3}}\right)\).
Rozwiązanie. Funkcja f jest stale równa zero: f(x) = 0.
Rzeczywiście, jeśli do wykresu funkcji f należy punkt A=(x;y), to należy do niego też punkt A' symetryczny do A względem osi OX, czyli punkt A' = (x; − y). Z drugiej strony funkcja może mieć dla argumentu x tylko jedną wartość, więc musi być spełniona równość:
y = − y
Stąd y=0. A zatem, w szczególności:
\(f(\sqrt{\pi}+\sqrt{2+\sqrt{3}})=0\).
Zadanie 2.7. Wykres funkcji:
\(f\left(x\right)=|x-1|-1\)
odbito symetrycznie względem prostej y=1, uzyskując wykres funkcji g. Jaki wzór ma ta funkcja?
Rozwiązanie. Rysujemy najpierw wykres funkcji f, zauważając, że jest to wykres funkcji V(x) = | x | przesunięty o wektor [1;-1]. Następnie rysujemy obraz wykresu funkcji f w symetrii względem prostej y=1:
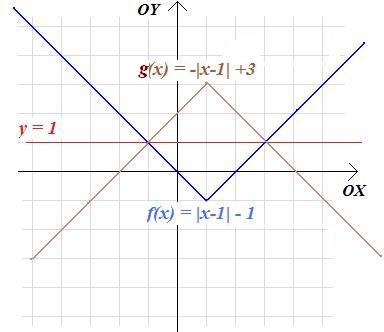
Zauważamy teraz, że uzyskany wykres jest wykresem funkcji W(x) = − | x | przesuniętym o wektor [1;3]. Jest to zatem wykres funkcji danej równaniem:
\(g\left(x\right)=-|x-1|+3\)
Zadanie 2.8. Wykres funkcji:
\(f\left(x\right)=|x-1|-2\)
odbito symetrycznie względem prostej x = − 1, uzyskując wykres funkcji g. Jaki wzór ma ta funkcja?
Rozwiązanie. Rysujemy najpierw wykres funkcji f, zauważając, że jest to wykres funkcji V(x) = | x | przesunięty o wektor [1;-2]. Następnie rysujemy obraz wykresu funkcji f w symetrii względem prostej x=-1, zauważając, że skoro czubek wykresu funkcji f jest w punkcie A=(1;-2), to czubek wykresu funkcji g znajdzie się w punkcie A'=(-3;-2).
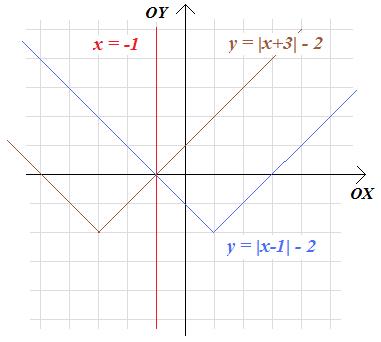
Widzimy teraz, że uzyskany wykres jest wykresem funkcji V(x)=|x| przesunietym o wektor [-3;-2]. Wzór funkcji g jest więc następujący:
\(g\left(x\right)=|x-(-3)|-2=|x+3|-2\)
Zadanie 2.9. Wykres funkcji:
\(f\left(x\right)=|x-2|+1\)
obrócono wokół początku układu współrzędnych o kąt 180 stopni, tak, że stał się on wykresem pewnej funkcji g. Jaki wzór ma funkcja g?
Wskazówka. Obrót o 180 stopni to symetria środkowa względem środka obrotu.
Rozwiązanie. Skoro obrót o 180 stopni, to symetria środkowa, więc z Twierdzenia 2.6. wynika, iż:
\(g(x)=-f(-x)=-\left(|-x-2|+1\right)=-|x+2|-1\)
Zadanie 2.10. Wykres funkcji:
\(f\left(x\right)=|x|+1\)
odbito symetrycznie względem punktu (1;0). Czy uzyskana figura jest wykresem pewnej funkcji g? Jeśli tak, to jakiej?
Rozwiązanie. Zadanie najprościej rozwiązać, szkicując odpowiedni wykres i odbijając go symetrycznie względem punktu (1;0):
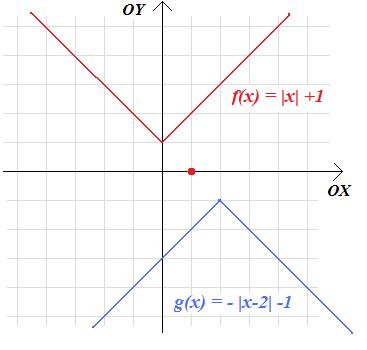
Widzimy, że uzyskany wykres jest wykresem funkcji W(x) = − | x | przesuniętym o wektor [2;-1]. A zatem jest to wykres funkcji:
\(g\left(x\right)= - |x-2|-1\)
Zadanie 2.11. Wykaż, że wykres funkcji f(x) = | x | po obróceniu wokół punktu (0;0) o kąt \(\alpha=45^{\circ}\) w kierunku przeciwnym do ruchu wskazówek zegara nie jest wykresem żadnej funkcji zmiennej x.
Rozwiązanie. Po obróceniu wykres funkcji f(x)=|x| pokryje ujemną część osi OX i dodatnią część osi OY:
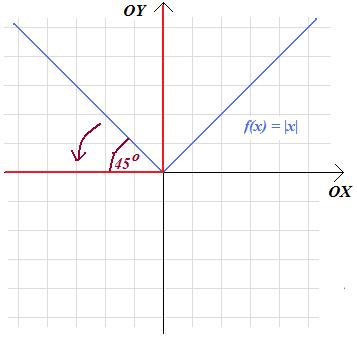
Otrzymana figura nie jest więc wykresem funkcji, bo dla x=0 domniemana funkcja musiałaby przyjąć nieskończenie wiele wartości, co oczywiście nie jest możliwe.
Zadanie 2.12. O jaki kąt wokół punktu (0;0) można obrócić wykres funkcji:
\(f(x)=\sqrt{x^2-1}\),
by otrzymać wykres pewnej innej funkcji?
Wskazówka. Częścią jakiej figury jest wykres funkcji f?
Rozwiązanie. Na początku zauważamy, że wykres funkcji jest górną połówką okręgu o równaniu:
x2 + y2 = 1.
Rzeczywiście, warunki:
1. y jest liczbą nieujemną i spełnia równanie: x2 + y2 = 1,
oraz
2. \(y=\sqrt{x^2-1}\)
są równoważne, bo pierwiastki kwadratowe zawsze są nieujemne.
Skoro wykres funkcji jest górną połówką odpowiedniego okręgu, to widzimy już, że jakikolwiek obrót wokół środka okręgu o kąt różny od wielokrotności kąta półpełnego prowadzi do figury, która nie jest wykresem żadnej funkcji zmiennej x, bo dla każdej połówki rozważanego okręgu, różnej od górnej lub dolnej połówki, zawsze znajdziemy pionową prostą przecinającą ową połówkę w dwóch różnych punktach:
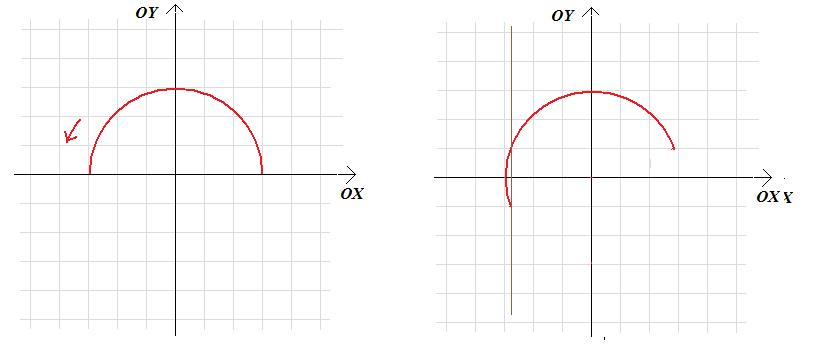
Zadanie 2.13. Narysuj wykresy funkcji:
a. \(f\left(x\right)=2|x|\) b. \(f(x)=\frac{1}{2}|x|\)
Rozwiązanie. W przypadku a. musimy wykres funkcji g(x)=|x| rozciągnąć dwukrotnie w kierunku pionowym. W przypadku b wykres g trzeba ścisnąć dwukrotnie w kierunku pionowym. Otrzymujemy zatem następujące wykresy:
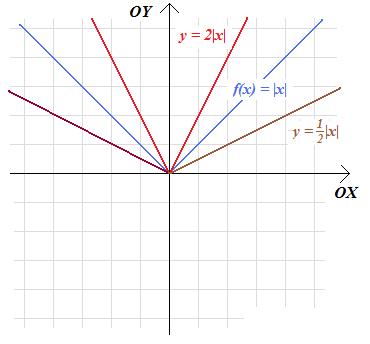
Zadanie 2.14. Narysuj wykres funkcji:
\(f\left( x \right)=||x+1|-1|\)
Rozwiązanie Najpierw - zgodnie z Twierdzeniem 2.3. - wykres funkcji g(x)=|x| przesuwamy o wektor [-1;-1], a następnie odbijamy względem osi OX część wykresu położoną poniżej osi. Stąd wykres f wygląda następująco:
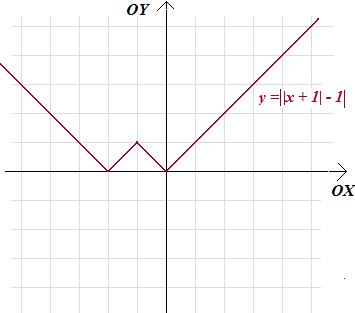
Zadanie 2.15. Wykaż, że jeśli funkcja g jest funkcją odwrotną do f, to wykres g jest symetryczny do wykresu f względem prostej y=x.
Wskazówka. Obrazem punktu (x,y) w symetrii względem prostej y = x jest punkt (y;x), co można wywnioskować analizując poniższy rysunek:
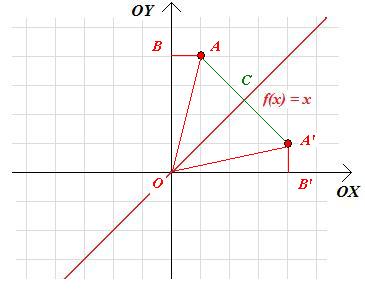
Rozwiązanie. Załóżmy, że punkt A=(x;y) należy do wykresu funkcji f. Oznacza to, że argumentowi x funkcja f przyporządkowuje liczbę y. Ponieważ funkcja g jest odwrotna do funkcji f, więc musi ona - zgodnie z definicją - przypisywać liczbie y liczbę x. A zatem punkt (y,x) musi należeć do wykresu funkcji g. Podobnie, jeśli do wykresu g należy punkt (y;x), to do wykresu f musi należeć punkt (x;y). Ze wskazówki wynika więc, że g jest funkcją odwrotną do funkcji f wtedy i tylko wtedy, gdy wykresy f oraz g są symetryczne względem prostej y=x.
