Rozpatrzymy teraz funkcję, która danej liczbie rzeczywistej różnej od zera przypisuje jej odwrotmość. Funkcja ta dana jest wzorem:
\(f\left(x\right)=\frac1x.\)
Jej wykres wygląda następująco:
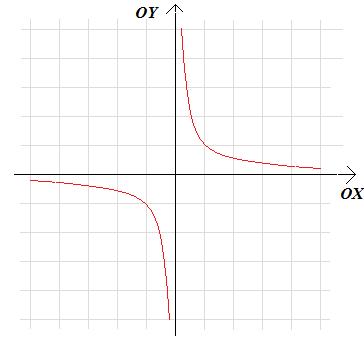
i nazywany jest hiperbolą.
Zwróćmy teraz uwagę, że wykorzystując odpowiednie przekształcenia wykresu uzyskamy całą serię wykresów funkcji ściśle związanych z funkcją \(f(x)=\frac1x\). Rzeczywiście:
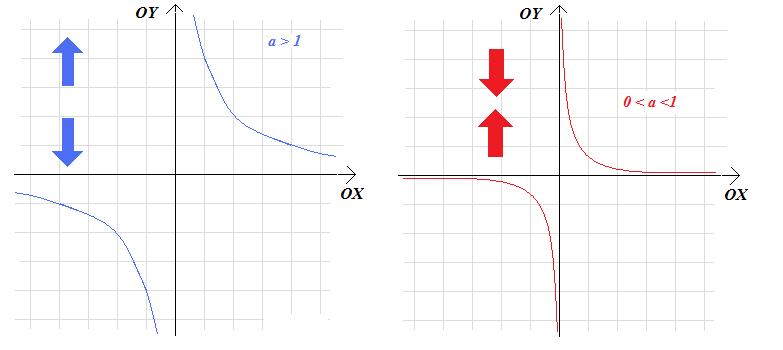
- rozciągając lub ściskając wykres w kierunku poziomym lub pionowym z wykresu funkcji:
\(f(x)=\frac{1}{x}\)
uzyskamy wykres funkcji
\(g(x)=\frac{a}{x}\)
dla a>0.
- odbijając symetrycznie względem osi OX lub OY wykres funkcji
\(g(x)=\frac{a}{x}\)
dostaniemy wykres funkcji
\(k(x)=-\frac{a}{x}\). 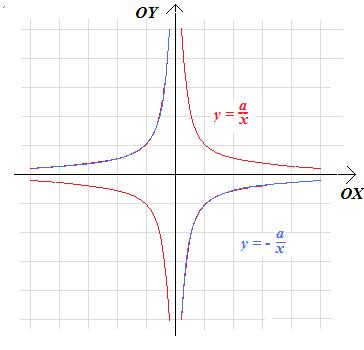
- przesuwając wykres funkcji
\(g(x)=\frac{a}{x}\)
o wektor [p;q] otrzymamy wykres funkcji
\(h(x)=\frac{a}{x-p}+q\). 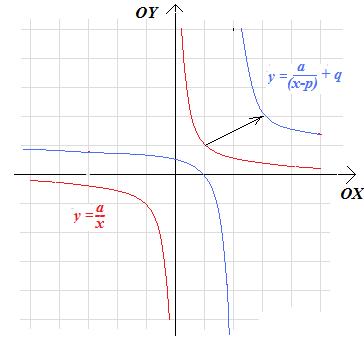
Zauważmy, że wzór funkcji h z ostatniego przykładu możemy - poprzez sprowadzenie obu składników sumy do wspólnego mianownika - zapisać w bardziej zwartej postaci ułamka, w którego liczniku oraz mianowniku występują pewne wyrażenia liniowe.
|
Definicja 5.1. Homografią nazywamy funkcję f, którą nie jest funkcją stałą, i którą można zapisać w postaci: \(f(x)=\frac{ax+b}{cx+d},\) gdzie a, b, c oraz d są liczbami rzeczywistymi.
|
|
Twierdzenie 5.2. Wykresem każdej homografii, która nie jest funkcją liniową jest hiperbola.
|
Zadania
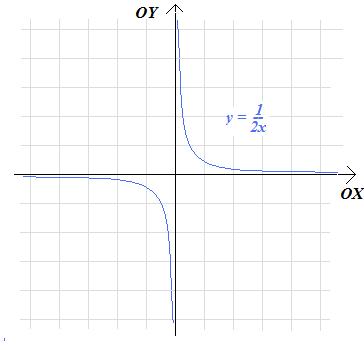
Zadanie 3.39. Narysuj wykres funkcji:
a. \(f(x)=\frac{1}{2x}\)
b. \(f(x)=\frac{2}{x}\)
Rozwiązanie. W każdym z powyższym przypadków funkcja f nie jest zdefiniowana dla x=0.
a. Do wykresu f należą punkty:
\(\left(\frac14,2\right), \left(\frac12,1\right), \left(1,\frac12\right),\left(2,\frac14\right), \left(4;\frac18\right).\)
Ponadto do wykresu f należą punkty:
\(\left(-\frac14,-2\right), \left(-\frac12,-1\right), \left(-1,-\frac12\right),\left(-2,-\frac14\right), \left(-4;-\frac18\right).\)
łączymy punkty każdej gałęzi hiperboli ciągła linią. Zbliżając się do zera od prawej strony, uciekamy w górę, zbliżając się od strony lewej, uciekamy w dół. Wykres wygląda więc następująco:
b. Postępując podobnie jak w punkcie a. uzyskujemy wykresy:
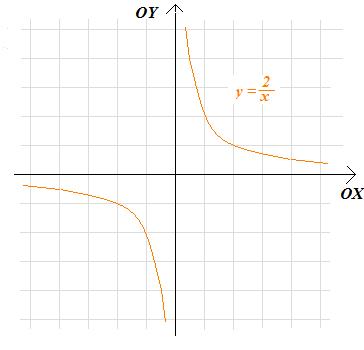
Zadanie 3.40. Narysuj wykres funkcji:
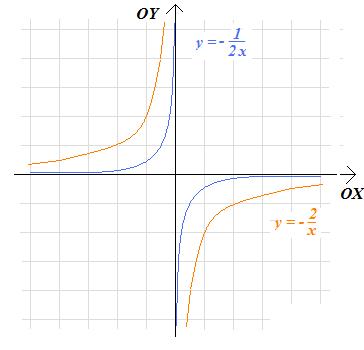
a. \(f(x)=-\frac{1}{2x}\) b. \(f(x)=-\frac1x\) c. \(f(x)=-\frac2x\)
Rozwiązanie. Odbijamy wykresy funkcji:
\(f(x)=\frac{1}{2x}\), \(f(x)=\frac1x\), \(f(x)=\frac2x\)
względem osi OX (lub OY). Stąd szukane wykresy wyglądają następująco:
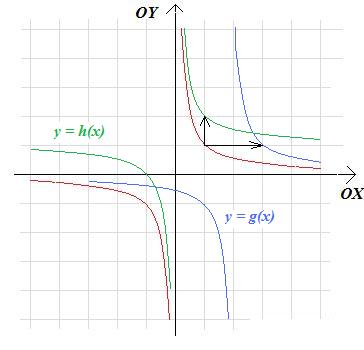
Zadanie 3.41. Narysujemy wykres funkcji:
a. \(g(x)=\frac{1}{x-2}\)
b. \(h(x)=\frac{1}{x}+1\)
Rozwiązanie. Przesuwamy wykres funkcji:
\( f(x)=\frac1x\)
o wektor:
a. [2;0]
b. [0;1]
Stąd otrzymujemy wykresy:
Zadanie 3.42. Znajdź wektor, o jaki należy przesunąć wykres funkcji:
\(f(x)=\frac{a}{x}\)
dla pewnego \(a\in \mathbb{R},\) by narysować wykres funkcji:
a. \(f(x)=\frac{2x+1}{x-2}\) b. \(f(x)=\frac{x-1}{x+3}\)
Rozwiązanie. W przypadku a mamy:
\(f(x)=\frac{2x+1}{x-2}= \frac{2(x-2)+3}{x-2}=2+\frac{3}{x-2}\)
A zatem, aby narysować wykres funkcji f należy wykres fukcji:
\(f(x)=\frac{3}{x}\)
przesunąć o wektor [2;2]
W przypadku b. mamy
\(f(x)=\frac{x-1}{x+3}= \frac{x+3-4}{x+3}=1-\frac{4}{x+3}\)
A zatem aby narysować wykres funkcji f należy wykres fukcji:
\(f(x)=-\frac{4}{x}\)
przesunąć o wektor [-3;1].
Zadanie 3.43. Znajdź najmniejszą wartość funkcji:
\(f(x)=\frac{1}{x+1}\)
na przedziale [0;3].
Rozwiązanie. Wykres funkcji f jest przesuniętą o wektor [-1;0] hiperbolą
\(y=\frac{1}{x}\)
A zatem funkcja f jest ściśle malejąca na przedziale \((-1;+\infty)\). Stąd najmniejsza wartość funkcji f na przedziale [0;3] jest równa:
\(f(3)=\frac{1}{1+3}=\frac14.\)
Zadanie 3.44. Znajdziemy największy przedział zawierający -7, na którym funkcja:
\(f(x)=\frac{x-1}{x+1}\)
jest rosnąca.
Rozwiązanie. Zauważmy najpierw, że
\(f(x)=\frac{x-1}{x+1}=1-\frac{2}{x+1}\)
A zatem wykres f powstaje z wykresu funkcji:
\(f(x)=-\frac{2}{x+1}\)
o wektor [-1;1].
Jasne jest zatem, że f rośnie na przedziale \(I=(-\infty; -1).\) Na żadnym większym zbiorze już nie rośnie, bo dla x=-1 nie jest określona, a dla x>-1 przyjmuje wartości ujemne, czyli mniejsze od tych osiąganych na przedziale I.
Zadanie 3.45. Wykaż, że jeśli ad-bc=0, to funkcja
\(f(x)=\frac{ax+b}{cx+d}\)
jest funkcją stałą.
Rozwiązanie. Możliwe są dwa przypadki: albo c=0, albo nie.
Przypadek I. Jeśli c=0, to z warunku ad-bc=0 wynika, że a lub d jest równe zero. Liczba d nie może być równa zero, bo wtedy mianownik: cx+d byłby równy zero i wzór nie określałby żadnej funkcji. Jeśli więc c=0, to także a =0 i wtedy:
\(f(x)=\frac{b}{d}= const\)
Przypadek II. Jeśli z kolei \(c\neq 0\), to
\(f(x)=\frac{ax+b}{cx+d}=\frac{\frac{a}{c}(cx+d)-\frac{ad}{c}+b}{cx+d}= \frac{a}{c}-\frac{ad-bc}{c(cx+d)}=\frac{a}{c}-0=\frac{a}{c}=const\)
Zadanie 3.46. Wykaż, że prosta y=-x+2 ma tylko jeden punkt wspólny z hiperbolą:
\(y=\frac{1}{x}\)
Rozwiązanie. Rozwiążmy układ równań:
\(\left\{\begin{array}{cc} y = & \frac{1}{x} \\ y = & -x +2 \end{array} \right.\)
Podstawiając y z drugiego równania do pierwszego, otrzymujemy:
\(-x+2=\frac{1}{x}\)
Stąd wynika, że
− x2 + 2x = 1
czyli
(x − 1)2 = 0.
Równanie to ma tylko jedno rozwiązanie: x = 1. Stąd jedyny punkt wspólny hiperboli:
\(y=\frac{1}{x}\)
i prostej y = − x + 2 to punkt (1;1).
Zadanie 3.47. Znajdź współczynnik kierunkowy prostej, która styka się z hiperbolą:
\(y=\frac{1}{x}\)
jedynie w punkcie:
\(A=\left(s,\frac{1}{s}\right).\)
Rozwiązanie. Każda prosta przechodząca przez punkt A ma równanie:
\(y=a(x-s)+\frac{1}{s}\)
dla pewnej liczby rzeczywistej a. Szukamy zatem takiego a, by równanie
\(a(x-s)+\frac{1}{s}=\frac{1}{x}\)
miało tylko jedno rozwiązanie (x=s). Stąd, równanie:
\(ax^2+\left(\frac{1}{s}-as\right)x-1=0\)
musi mieć deltę równą zero:
\(\Delta =\left(\frac{1}{s}-as\right)^2+4a = a^2s^2-2a+\frac{1}{s^2}+4a=\left(as+\frac{1}{s}\right)^2=0\)
Stąd:
\(a=-\frac{1}{s^2}\).
Zadanie 3.48. Wykaż, że prosta y = x jest osią symetrii wykresu funkcji
a. \(f(x)=\frac{5}{x}\)
b. \(g(x)= \frac{5}{x-3}+3.\)
Rozwiązanie. Niech punkt (m;s) należy do wykresu f. Wtedy:
\(s=\frac{5}{m}\)
Wynika stąd, że punkt (s;m), który jest symetryczny do (m;s) względem prostej y=x, także należy do wykresu f, gdyż:
\(f(s)=\frac{5}{\frac{5}{m}}=m\)
b. Wykres g to wykres funkcji f z podpunktu a przesunięty o wektor [3;3], czyli przesunięty wzdłuż prostej y = x. Skoro wyjściowy wykres jest symetryczny względem prostej y = x, to także po przesunięciu jest on względem niej symetryczny.
Zadanie 3.49. Udowodnij, że wykres funkcji:
\(f\left(x\right)=\frac{a}{x-p}+q\)
dla \((a\neq0)\) jest symetryczny do wykresu funkcji:
\(g\left(x\right)=\frac{a}{x-q}+p\)
względem prostej y=x.
Rozwiązanie. Wykres f powstaje z przesunięcia o wektor v=[p;q] wykresu funkcji:
\(h(x)=\frac{a}{x}\)
Wykres g powstaje z przesunięcia wykresu funkcji h o wektor w=[q;p].
Zauważmy teraz, że:
1) prosta y = x jest osią symetrii wykresu funkcji h (rozumujemy podobnie jak w poprzednim zadaniu) oraz, że
2) wektor v=[p;q] jest symetryczny do wektora w=[q;p] względem prostej y=x.
Weźmy jakikolwiek punkt A należący do wykresu h i niech A' będzie symetrycznym do niego punktem względem prostej y=x.
Jeśli punkt A przesuniemy o wektor v=[p;q], to otrzymamy punkt B należący do wykresu funkcji f.
Jeśli punkt A' przesuniemy o wektor w=[q;p], to otrzymamy punkt B' należący do wykresu g.
Punkty B i B' są jednak symetryczne względem prostej y=x, bo A i A' są względem niej symetryczne podobnie jak wektory v i w.
Zadanie 3.50. Znajdź funkcję g, której wykres jest symetryczny względem prostej y=x do wykresu funkcji:
\(f(x)=\frac{5}{x-11}+7\)
Rozwiązanie. Z poprzedniego zadania wynika, że
\(g(x)=\frac{5}{x-7}+11\)
Zadanie 3.51. Wykaż, że dla każdej homografii f istnieje homografia g taka, że dla dla wszystkich x z wyjątkiem, być może, jednego punktu:
\(g\left(f(x)\right)=x\)
Rozwiązanie. Jeśli f jest funkcją liniową (która nie jest stała! - to zakładaliśmy w definicji homografii), to teza wynika z zadania 3.10.
Jeśli f nie jest liniowa, to da się zapisać w postaci:
\(f(x)=\frac{a}{x-p}+q\)
i biorąc
\(g(x)=\frac{a}{x-q}+p\)
otrzymujemy:
\(g(f(x))=\frac{a}{\frac{a}{x-p}+q-q}+p=x-p+p=x\)
Zadanie 3.52 Znajdź funkcję f taką, że:
\(f\left(\frac{2x-1}{x+2}\right) = x\)
dla każdej liczby rzeczywistej \(x\neq -2\).
Mamy:
\(f\left(\frac{2x-1}{x+2}\right) = \frac{2(x+2)-5}{x+2}=2-\frac{5}{x+2}\)
i korzystając z poprzedniego zadania, uzyskujemy:
\(g(x)=\frac{5}{x-2}-2\)
