Kolejną bardzo ważną funkcją jest funkcja, która danej liczbie rzeczywistej x przypisuje jej kwadrat. Funkcja taka dana jest wzorem:
\(f\left(x\right)=x^2\).
Jej wykres wygląda następująco:
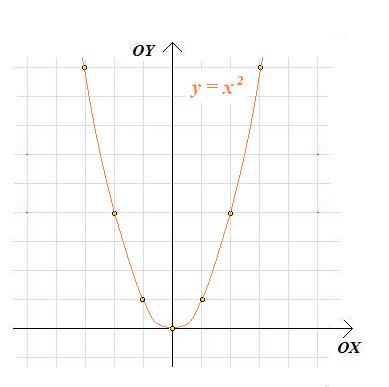
Przedstawiony powyżej wykres nazywany jest parabolą. Parabola y = x2 ma wierzchołek w punkcie (0;0) i oś symetrii o równaniu x=0. Części paraboli odpowiadającą x dodatnim oraz część odpowiadającą x ujemnym nazywamy ramionami paraboli.
Korzystając z przekształceń wykresu opisanych w poprzedniej części, możemy teraz z wykresu funkcji f(x) = x2 uzyskać całą serię innych wykresów:
- poprzez rozciąganie i ściskanie wykresu funkcji f(x) = x2 otrzymujemy wykresy funkcji postaci g(x) = ax2 dla a>0:
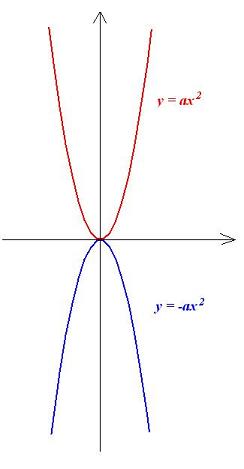
- odbicie względem osi OX (lub OY) wykresu funkcji f(x) = ax2 dla a>0 daje wykresy funkcji g(x)=ax^2 dla a<0:
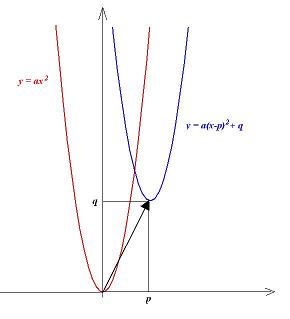
- przesunięcie o wektor [p;q] pozwala z wykresu funkcji g(x)=ax^2 uzyskać wykres funkcji h(x) = a(x − p)2 + q:
|
Definicja 4.1. Funkcją kwadratową w postaci kanonicznej nazywamy funkcję postaci: \(f\left(x\right)=a(x-p)^2+q.\) gdzie liczby a, p oraz q są rzeczywiste, przy czym a jest różne od zera.
|
Zauważmy, że zgodnie z twierdzeniem 2.3. wykresem funkcji f(x) = a(x − p)2 + q jest parabola y = ax2 przesunięta równolegle o wektor [p;q]. Wykres funkcji kwadratowej w postaci kanonicznej rysuje się więc łatwo.
Jeżeli jednak w postaci kanonicznej funkcji kwadratowej pozbędziemy się nawiasów, to otrzymamy wyrażenie postaci ax2 + bx + c, gdzie b oraz c to pewne liczby rzeczywiste.
|
Definicja 4.2. Funkcją kwadratową w postaci ogólnej nazywamy funkcję postaci: \(f\left(x\right)=ax^2+bx+c\), gdzie a, b i c to liczby rzeczywiste, przy czym a jest różne od zera.
|
Rysowanie paraboli y = ax2 + bx + c jest o wiele trudniejsze niż rysowanie paraboli y = a(x − p)2 + q i w gruncie rzeczy udaje się wykonać dopiero wówczas, gdy odpowiednią funkcję kwadratową daną w postaci ogólnej zapiszemy w postaci kanonicznej. Korzystamy w tym celu zwykle ze wzorów skróconego mnożenia. Jeśli okazuje się to zbyt trudne, możemy skorzystać z następującego twierdzenia, które podaje gotowe wzory na współczynniki p oraz q w zależności od wpsółczynników a, b oraz c:
|
Twierdzenie 4.3. Każda funkcja kwadratowa: \(f\left(x\right)=ax^2+bx+c\) da się zapisać w postaci kanonicznej: \(f(x)=a\left(x-p\right)^2+q,\) gdzie współczynniki p oraz q dane są wzorami: \(p=-\frac{b}{2a}\), \(q=-\frac{\Delta}{4a}\), Δ = b2 − 4ac.
|
Powyższe twierdzenie można zatem zapisać także następująco:
|
Twierdzenie 4.4. Każda funkcja kwadratowa: \(f\left(x\right)=ax^2+bx+c\) da się zapisać w postaci kanonicznej: \(f\left(x\right)=a(x-p)^2+q\), gdzie \(p=-\frac{b}{2a}\) oraz \(q=f\left(p\right)\).
|
Oprócz postaci kanonicznej i postaci ogólnej niektóre funkcje kwadratowe dane są w postaci iloczynowej.
|
Definicja 4.5. Funkcja kwadratowa f dana jest w postaci iloczynowej, jeśli zapisana jest następująco: \(f\left(x\right)=a(x-x_1)(x-x_2)\), gdzie liczby a, x1 oraz x2 są rzeczywiste.
|
O tym, czy dana funkcja kwadratowa da się zapisać w postaci iloczynowej, rozstrzyga następujące twierdzenie.
|
Twierdzenie 4.6. Niech dana będzie funkcja kwadratowa: \(f\left(x\right)=ax^2+bx+c\) Jeśli funkcja f ma dwa różne pierwiastki x1 oraz x2, to można ją zapisać w postaci iloczynowej: \(f\left(x\right)=a(x-x_1)(x-x_2)\) Jeśli f ma jeden pierwiastek równy x1 to da się zapisać w postaci: \(f\left(x\right)=a(x-x_1)^2\) Jeśli f nie ma pierwiastka, to nie da się zapisać w postaci iloczynowej. |
Zadanie 3.17. Naszkicuj wykres funkcji:
a. \(f(x)=\frac14 x^2\)
b. \(f(x)=\frac12 x^2\)
c. \(f\left(x\right)= 2x^2\)
d. \(f\left(x\right)=4x^2\)
Rozwiązanie. a. Obliczamy wartości funkcji dla kilku liczb np. dla x=-2, x=-1, x=0, x=1 oraz x=2. Wnioskujemy stąd, że punkty
\(\left(-2;1\right)\), \(\left(-1;\frac14\right),\) \(\left(0;0\right)\), \((1;\frac14),\) \((\left(2;1\right)\)
należą do wykresu funkcji f. Łączymy te punkty ciągła linią tak, by przypominała ona kształtem parabolę.
W punktach b, c oraz d, postępujemy podobnie jak w punkcie a, uzyskując ostatecznie wykresy:
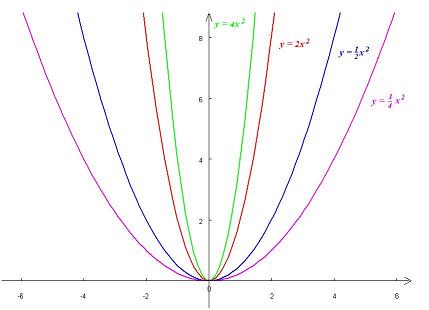
Zauważmy, że we wszystkich przypadkach narysowane parabole mają ramiona skierowane do góry. Ponadto wraz ze wzrostem wartości a, ramiona stają się coraz węższe.
Zadanie 3.18. Naszkicuj wykresy funkcji:
a. \(f(x)=-\frac14 x^2\)
b. \(f(x)=-\frac12 x^2\)
b. \(f\left(x\right)=-2x^2\)
c. \(f\left(x\right)=-4x^2\)
Rozwiązanie. Wykresy funkcji wyglądają następująco:
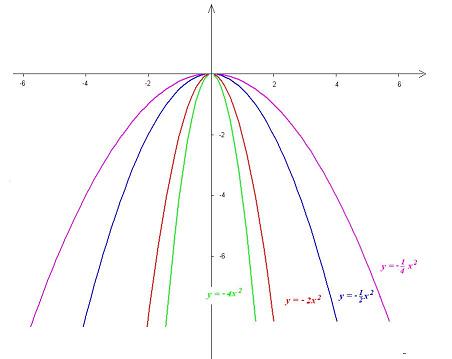
Zauważmy, że wszystkie parabole mają ramiona ramiona skierowane w dół. Jest tak zawsze, gdy współczynnik a jest ujemny.
Zadanie 3.19. Znajdź współrzędne wierzchołka paraboli
\(y=2\left(x-7\right)^2+6.\)
Rozwiązanie. Parabola:
\(y=2\left(x-7\right)^2+6\)
jest parabolą y = 2x2 przesuniętą o wektor [7;6]. A zatem jej wierzchołek znajduje się w punkcie (7;6).
Zadanie 3.20. Narysuj wykresy funkcji:
a. \(f\left(x\right)= (x+1)^2-1\) b. \(g\left(x\right)=-2(x-4)^2+3\)
Rozwiązanie. a. wykresem funkcji f jest parabola y = x2 przesunięta o wektor [-1;-1].
b. wykresem funkcji g jest parabola y = − 2x2 przesunięta o wektor [4;3].
Wykresy funkcji f i g są zatem następujące:
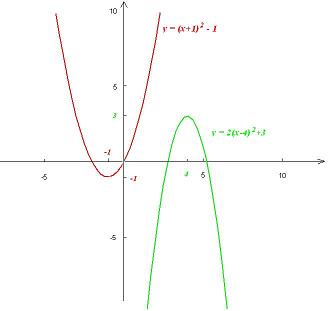
Zadanie 3.21. Naszkicuj wykres funkcji
a. \(f\left(x\right)=x^2+2x-3\) b. \(g\left(x\right)=2x^2+8x+9\)
Rozwiązanie. Korzystając ze wzorów skróconego mnożenia, mamy:
a. \(f\left(x\right)=x^2+2x-3=(x^2+2x+1)-1-3=(x+1)^2-4\) b. \(g\left(x\right)=2x^2+8x-2=2(x^2+4x+4)-2\cdot4+9=2(x+2)^2+1\)
A zatem wykresy funkcji f oraz g wyglądają następująco:
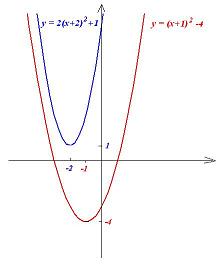
Zadanie 3.22. Naszkicuj wykres funkcji:
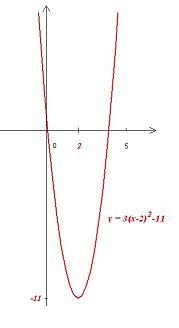
\(f\left(x\right)=3x^2-12x+1\)
Rozwiązanie. Wykresem funkcji f jest parabola y = 3x2 przesunięta o pewien wektor [p;q]. Korzystając z twierdzenia 4.3. mamy:
\(p=-\frac{-12}{2\cdot3}=2,\) \(q=f\left(2\right)=3\cdot 2^2-12\cdot2+1=-11.\)
Stąd:
\(f\left(x\right)=3(x-2)^2-11\)
i wykres f wygląda następująco:
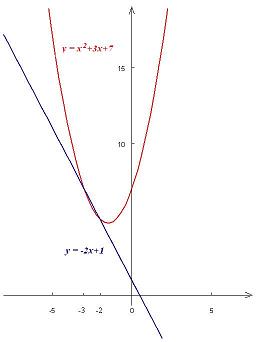
Zadanie 3.23. Znajdź przedziały, na których wykres funkcji:
\(f\left(x\right)=x^2+3x+7\)
leży ponad wykresem funkcji
\(g\left(x\right)=-2x+1\).
Rozwiązanie. Mamy:
\(f(x)>g(x) \Leftrightarrow x^2+3x+7>1-2x \Leftrightarrow x^2+5x+6> 0 \Leftrightarrow(x+2)(x+3) > 0\)
Mamy zatem rozwiązać nierówność:
\(\left(x+2\right)(x+3)>0\).
Rozpatrzmy parabolę:
\(y=\left(x+2\right)(x+3).\)
Ma ona miejsca zerowe: -2 oraz -3. Jej ramiona są skierowane w górę. Leży więc ona zawsze ponad osią OX z wyjątkiem przedziału [-3;-2]. Stąd:
\((x+2)(x+3)>0\Leftrightarrow x<-3\) lub x > − 2
Wykres funkcji f leży zatem ponad wykresem funkcji g na przedziale: \((-\infty; -3)\) oraz \((-2;+\infty).\)
Zadanie 3.24. Znajdź oś symetrii wykresu funkcji kwadratowej:
\(f\left(x\right)=(x+1)(x-3)\).
Rozwiązanie. Ze wzoru odczytujemy natychmiast pierwiastki funkcji f: są to liczby -1 oraz 3. Pierwiastki muszą być symetrycznie położone względem osi symetrii wykresu, a zatem oś symetrii musi mieć równanie x=c, gdzie c leży dokładnie w połowie odcinka o końcach (-1;3). Stąd:
\(c=\frac{-1+3}{2}=1\)
i szukana oś symetrii ma równanie: x=1.
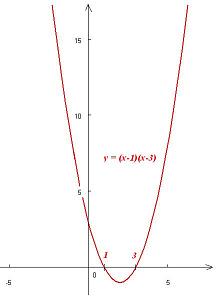
Zadanie 3.25. Naszkicuj wykres funkcji: f(x) = (x − 1)(x − 3).
Rozwiązanie. I sposób. Rozwijamy:
\(f\left(x\right)= (x-1)(x-3)=x^2-4x+3\)
i rysujemy wykres tak, jak w poprzednich przypadkach.
II sposób. Rozumując podobnie jak w poprzednim zadaniu zauważamy, że oś symetrii wykresu to prosta x=2. Ponieważ:
\(f\left(2\right)=(2-1)(2-3)=-1,\)
więc wierzchołek paraboli:
\(y=\left(x-1\right)(x-3)=x^2-4x+3\)
leży w punkcie (2;-1). Parabola ta jest oczywiście przesuniętą parabolą y = x2.
Wykres wygląda zatem następująco:
Zadanie 3.26. Wykaż, że największa wartość funkcji:
\(f\left(x\right)=4x-x^2\)
jest równa 4.
Rozwiązanie. I sposób. Standardowo znajdujemy współrzędne wierzchołka paraboli i szkicujemy wykres f. Widzimy, że najmniejsza wartość jest równa 4.
II sposób. Dowolnym sposobem sprowadzamy funkcję f do postaci kanonicznej:
\(f\left(x\right)=4x-x^2=-(x-2)^2+4\)
Widać, że \(f(x)\geq 4.\) Ponadto f(2) = 4. Zatem 4 jest największą z wartości funkcji f.
Zadanie 3.27. Wykaż, że funkcja
\(f\left(x\right)=x^2\)
jest rosnąca na przedziale \([0;+\infty)\).
Rozwiązanie:
\(0\leq x_1\leq x_2\).
Wtedy
\(x_2-x_1\geq 0\) oraz \(x_2+x_1\geq 0\).
Iloczyn dwóch nieujemnych wyrażeń musi być nieujemny więc:
\(0\leq (x_2+x_1)(x_2-x_1)=x_2^2-x_1^2.\)
Stąd:
\(f(x_1)\leq f(x_2)\).
Zadanie 3.28. Znajdź największy przedział, na którym funkcja:
\(f\left(x\right)=x^2+4x+3\)
jest ściśle rosnąca.
Rozwizanie. Mamy
\(f\left(x\right)=x^2+4x+3=(x+2)^2 -1\).
A zatem wykresem funkcji f jest parabola y = x2 przesunięta o wektor [-2;-1]. Stąd f jest ściśle rosnąca na przedziale \([-2;+\infty).\)
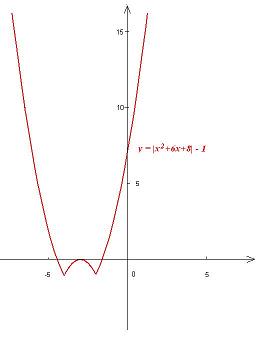
Zadanie 3.29. Naszkicuj wykres funkcji:
\(f\left(x\right)=|x^2+6x+8|-1\)
i znajdź jej wszystkie miejsca zerowe.
Rozwiązanie. Najpierw zapisujemy w postaci kanonicznej funkcję:
\(g\left(x\right)=x^2+6x+8=(x+3)^2-1\)
i rysujemy jej wykres. Następnie rysujemy wykres funkcji h(x)=|g(x)| i na koniec wykres samej funkcji f(x) = h(x) − 1.
Zadanie 3.30. Wykres funkcji:
\(f\left(x\right)=x^2-6x+8\)
odbito symetrycznie względem punktu A=(1;1), otrzymując wykres funkcji g. Jaki wzór ma ta funkcja?
Parabola
\(y=x^2+5x+6=\left(x-3\right)^2-1\)
ma wierzchołek w punkcie P=(3;-1). Punkt B symetryczny do punktu P względem punktu A ma współrzędne:
\(B=\left(1-2;1+2\right)=(-1;3).\)
Odbicie symetryczne względem punktu to po prostu obrót o kąt półpełny wokół tego punktu. Wykresem funkcji g jest więc parabola y = x2 odwrócona "do góry nogami" i o wierzchołku w punkcie (-1;3). Funkcja g dana jest więc wzorem:
\(g\left(x\right)=-(x+1)^2+3\),
a całą sytuację przedstawia rysunek:
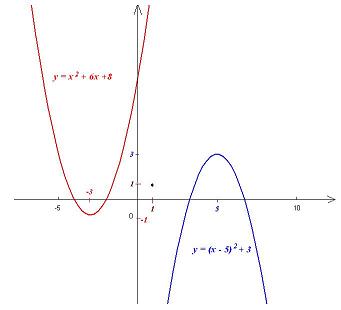
Zadanie 3.31. Udowodnij twierdzenie 4.3.
Rozwiązanie. Mamy:
\(ax^2+bx+c=a\left (x^2+2\cdot \frac{b}{2a}\cdot x\right) +c=a\left(x+\frac{b}{2a}\right)^2-a\frac{b^2}{4a^2}+c\) \( =a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\)
Zadanie 3.32. Udowodnij twierdzenie 4.4., korzystając z twierdzenia 4.3.
Rozwiązanie. Zauważamy, że:
\(f\left(p\right)=a(p-p)^2+q=q\).
Twierdzenie 4.4. wynika już teraz bezpośrednio z twierdzenia 4.3.
Zadanie 3.33. Udowodnij twierdzenie 4.6.
Rozwiązanie. Zapiszmy funkcję f w postaci kanonicznej:
\(f(x)=ax^2+bx+c=a\left(x-\frac{b}{2a}\right)^2-\frac{\Delta}{4a}\)
Jeśli funkcja f ma przynajmniej jeden pierwiastek, to
\(\Delta\geq 0\)
i w konsekwencji:
\(a\left(x-\frac{b}{2a}\right)^2-\frac{\Delta}{4a}= a\left[\left(x-\frac{b}{2a}\right)^2- \left(\frac{\sqrt{\Delta}}{2a}\right)^2\right]=a(x-x_1)(a-x_2),\)
gdzie w ostatniej równości wykorzystaliśmy wzór na różnicę kwadratów oraz wzór na pierwiastki równania kwadratowego. Gdy Δ = 0, to x1 = x2.
Jeśli z kolei Δ < 0, to pierwiastków f w ogóle nie ma i zapis w postaci iloczynowej jest niemożliwy, gdyż funkcja:
\(f\left(x\right)=a(x-x_1)(x-x_2)\)
ma niewątpliwie pierwiastek równy x1.
Zadanie 3.34. Znajdź prostą, która dotyka paraboli y = x2 w punkcie (1;1) i poza tym punktem nie ma z nią innych punktów styczności.
Rozwiązanie. Na początek zauważamy, że prosta, która nie jest równoległa do osi OY i przechodzi przez punkt (1;1) ma równanie y = ax + (1 − a). Chcemy, by ta prosta stykała się z odpowiednią parabolą tylko w jednym punkcie, tzn. żeby układ równań:
\(\left \{ \begin{array}{cc} y = & ax+1-a \\ y = & x^2 \\ \end{array} \right.\)
miał dokładnie jedno rozwiązanie. Aby tak było równanie
x2 = ax − a + 1
musi mieć dokładnie jedno rozwiązanie. Przenosimy wszystkie wyrazy na lewą stronę:
x2 − ax + (a − 1) = 0
i obliczamy deltę. Jak wiadomo, aby równanie kwadratowe miało dokładnie jedno rozwiązanie, delta musi być równa zero:
\(\Delta=a^2-4a+4=0\Leftrightarrow (a-2)^2=0\Leftrightarrow a=2.\)
A zatem szukana prosta ma równanie:
y = 2x − 1
Zauważmy, że jest to prosta najlepiej przylegająca do paraboli y = x2 w punkcie (1;1). Możemy powiedzieć, że w okolicy tego punktu funkcja kwadratowa rośnie podobnie jak prosta y = 2x − 1.
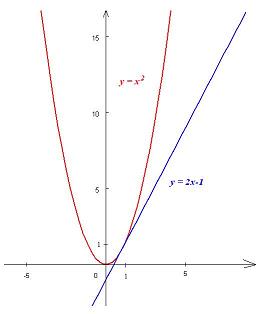
Zadanie 3.35. Znajdź współczynnik kierunkowy prostej, która dotyka paraboli y = x2 w punkcie (s,s2) i poza tym punktem nie ma z nią innych punktów styczności.
Rozwiązanie. Jeśli prosta y = ax + b przechodzi przez punkt (s,s2), to
s2 = as + b,
więc
b = s2 − as.
Stąd nasza prosta ma równanie y = ax + s2 − as. Chcemy, by ta prosta stykała się z parabolą y = x2 tylko w jednym punkcie, tzn. żeby układ równań:
\(\left \{ \begin{array}{cc} y = & ax+s^2-as \\ y = & x^2 \\ \end{array} \right.\)
miał dokładnie jedno rozwiązanie. Aby tak było równanie
x2 = ax + s2 − as
musi mieć dokładnie jedno rozwiązanie. Przenosimy wszystkie wyrazy na lewą stronę:
x2 − ax − (s2 − as) = 0
i obliczamy deltę:
\(\Delta=a^2+4s^2-4as=0\Leftrightarrow (a-2s)^2=0\Leftrightarrow a=2s.\)
A zatem szukany współczynnik kierunkowy jest równy 2s.
Zadanie 3.36. Znajdziemy zbiór wszystkich tych punktów, które są wierzchołkami pewnej paraboli o równaniu:
y = x2 + 2x + c
Rozwiązanie. Dla c = 0 uzyskujemy parabolę y = x2 + 2x o osi symetrii x = − 1. Zmieniając parametr c przesuwamy tę parabolę o wektor [0;c]. A zatem zbiór wierzchołków tak przesuwanych parabol to prosta o równaniu x = − 1.
Współczynnik c odpowiedzialny jest zatem za przesuwanie wykresu wzdłuż jego osi symetrii.
Zadanie 3.37. Znajdziemy zbiór wszystkich tych punktów, które są wierzchołkami pewnej paraboli o równaniu:
y = x2 + 2bx + 1
Rozwiązanie. Zauważmy, że dla danego b wierzchołek paraboli
y = x2 + 2bx + 1
leży w punkcie o współrzędnych (p,q), gdzie
\(p = -\frac{2b}{2}\)
oraz
\(q=f\left(p\right)=b^2-2b^2+1=-b^2+1\)
Każdy punkt postaci:
\(\left(-b; -b^2+1\right)\)
dla pewnego b leży na paraboli y = − x2 + 1. Ponieważ b może być dowolną liczbą rzeczywistą, więc zbiór wierzchołków rozważanych parabol tworzy parabolę o równaniu:
y = − x2 + 1.
Widzimy zatem, że współczynnik b jest odpowiedzialny za przesuwanie wykresu funkcji kwadratowej wzdłuż pewnej paraboli.
Zadanie 3.38. Znajdziemy zbiór wszystkich tych punktów, które są wierzchołkami pewnej paraboli o równaniu:
y = ax2 + x + 1
Rozwiązanie. Wierzchołek paraboli y = ax2 + x + 1 leży w punkcie (p,q), gdzie
\(p=-\frac{1}{2a}\)
oraz
\(q= f\left(p\right)=a\cdot \frac{1}{4a^2}-\frac{1}{2} a+1=-\frac14\frac{1}{a}+1=\frac{1}{2}\left(-\frac{1}{2a}\right)+1\)
Zależność między p oraz q możemy więc przedstawić następująco:
\(q=\frac{1}{2}p+1\)
Zbiór wierzchołków parabol postaci y = ax2 + x + 1 to zatem prosta:
\(y=\frac12 x+1\)
z wyjątkiem punktu (0,0) - gdyż p jest zawsze różne od zera. Zauważmy przy tym, że parabole rozważanej postaci mają ramiona tym bardziej rozłożone im dalej ich wierzchołek leży od punktu (0;0). Współczynnik a pełni więc w rozważanym przykładzie dwojaką funkcję: zmienia rozwartość ramion parabol i przesuwa je wzdłuż pewnej prostej.
