Oprócz możliwości dokładnego obliczenia dowolnego wyrazu ciągu, często warto umieć powiedzieć coś o zachowaniu całego ciągu, na przykład "ciąg (an) rośnie bardzo szybko", "ciąg (bn) jest malejący, wszystkie jego wyrazy są większe od − 1" albo nawet "zachowanie ciągu (cn) dla początkowych wyrazów trudno krótko opisać, ale dla indeksów n większych od 1000 wyrazy tego ciągu są bliskie 17,58".
Jak widać, opisywanie zachowania ciągu ułatwiają nam pojęcia ograniczoności i monotoniczności. Jeszcze lepiej pewne własności pozwoli wyrazić pojęcie granicy ciągu.
Intuicyjnie, granica ciągu to liczba, w pobliżu której skupiają się dalekie wyrazy ciągu.
|
Definincja 1. Liczba rzeczywista g jest granicą ciągu liczbowego (an), jeśli dla dowolnej liczby rzeczywistej ε > 0 istnieje \(n_0\in \mathbb{N}\) takie, że dla każdego \(n \in \mathbb{N}\), n > n0, zachodzi | an − g | < ε. |
Zamiast | an − g | < ε zwykle łatwiej sprawdzać osobno dwa warunki: an − g > − ε i an − g < ε.
Jeśli ciąg (an) ma granicę, to mówimy, że (an) jest zbieżny.
Jeśli g jest granicą ciągu (an), to mówimy, że ciąg (an) jest zbieżny do liczby g, co oznaczamy
\(a_n \rightarrow g\)
lub
\(\lim_{n \rightarrow \infty} a_n = g\).
Możemy też powiedzieć, że ciąg (an) dąży do wartości g.
Zacznijmy od końca, czyli od nierówności | an − g | < ε. Wartość | an − g | to odległość między an i g na osi liczbowej. Chcemy, żeby dla pewnych n ta odległość była mniejsza od wybranego ε - jeśli ε jest małe, to oznacza po prostu, że an ma być blisko g.
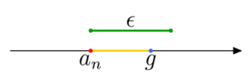
Możemy przeanalizować trochę większy fragment: widzimy, że an ma być nie dalej niż o ε od g dla wszystkich indeksów n większych od pewnego n0. Jeśli spojrzymy na wykres i zakryjemy na nim początkową część, zawierającą wyrazy ciągu od a1 aż do \(a_{n_0}\), to niezakryte wyrazy muszą się mieścić w pasie o szerokości ε w górę i ε w dół od prostej na wysokości g. Liczba n0 wyznacza końcówkę, "ogon" ciągu, który jest nie dalej niż o ε od g.
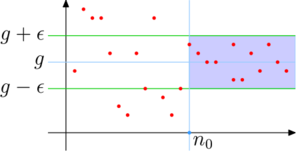
Spójrzmy wreszcie na całość definicji: chcemy umieć dobrać n0 takie, że wyrazy ciągu za \(a_{n_0}\) są nie dalej niż o ε od g dla dowolnej liczby rzeczywistej dodatniej ε. Tak naprawdę rozważanie dużych wartości ε nic nam tu nie daje. Chcemy sprawdzać, czy wyrazy ciągu są blisko pewnej liczby g - sprawdzenie, czy są od niej nie dalej niż o 1/5000, oczywiście pomaga nam bardziej, niż sprawdzenie, czy są nie dalej niż 5000 od g. To oznacza, że musimy umieć dobrać odpowiednie n0 dla dowolnie małej liczby rzeczywistej dodatniej ε.
Zwróćmy uwagę na kolejność warunków w definicji. Dobieramy wartość n0 do liczby ε > 0 - to absolutnie nie musi (a wręcz zazwyczaj nie może) być ta sama wartość dla różnych ε! Chcemy, żeby dla dowolnie wybranego ε, jakkolwiek małe by ono nie było, istniało w ciągu miejsce, od którego począwszy wyrazy ciągu nie odejdą od g dalej niż o ε. Jeśli będziemy zmniejszać ε, to miejsce zazwyczaj będzie się odsuwało w kierunku \(+\infty\) - trzeba będzie zakryć więcej początkowych wyrazów ciągu, żeby te niezakryte mieściły się w odpowiednim pasie.
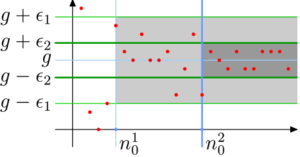
Przyjrzyjmy się pojęciu granicy na fundamentalnych i ciekawych przykładach.
Przykład 0.
Jaka jest granica ciągu stałego cn = c? Oczywiście, dla dowolnego ε > 0 liczba c jest nie dalej niż o ε nie tylko od wyrazów z pewnej końcówki ciągu, ale od wszystkich wyrazów ciągu. Wobec tego ciąg stale równy c jest zbieżny do c.
Przykład 0,5.
Niech teraz ciąg (cn) będzie stały od pewnego miejsca, czyli istnieje liczba \(K \in \mathbb{N}\) taka, że dla n > K zachodzi cn = c. W tym przypadku granicą ciągu (cn) również jest c, ponieważ na granicę nie ma wpływu początek ciągu - wystarczy za każdym razem wybierać \(n_0 \geq K\).
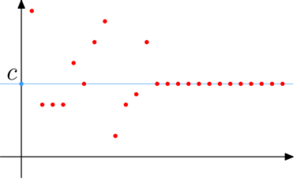
Przykład 1.
Zobaczmy prosty przykład: \(a_n = \frac{1}{n}\).
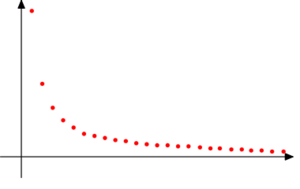
Oczywiście wszystkie wyrazy ciągu (an) są dodatnie. Ciąg an jest malejący: dla dowolnego \(n \in \mathbb{N}\) zachodzi \(a_n = \frac{1}{n} > \frac{1}{n+1} = a_{n+1}\), czyli kolejne wyrazy są coraz bliżej zera. Intuicja podpowiada nam, że zero faktycznie jest granicą tego ciągu. Jak to dokładnie wykazać? Przypomnijmy sobie definicję granicy. Zaczyna się "dla dowolnego ε > 0...", więc weźmy dowolne ε > 0.
Dalej musimy wykazać, że umiemy dobrać n0 tak, żeby spełnić warunek z definicji. W naszym przypadku \(a_n = \frac{1}{n}\) i liczba podejrzana o bycie granicą to g = 0, więc warunek mówi, że \(|\frac{1}{n} - 0| = \frac{1}{n} < \epsilon\), co jest równoważne nierówności \(\frac{1}{\epsilon} < n\). Czyli chcemy znaleźć n0 takie, że dla dowolnego n > n0 spełniona była nierówność \(n > \frac{1}{\epsilon}\). Możemy przyjąć za n0 dowolną liczbę naturalną większą od \(\frac{1}{\epsilon}\) - wtedy \(n > n_0 > \frac{1}{\epsilon}\), czyli potrzebna nam nierówność będzie spełniona!
Wobec tego g = 0 spełnia warunki z definicji 1, więc jest granicą ciągu \(a_n = \frac{1}{n}\).
Przykład 2. Nie każdy ciąg ma granicę.
(a) Niech (bn) będzie ciągiem, w którym na miejscach nieparzystych występują zera, a na parzystych jedynki (czyli \(b_n = n \mod 2\), gdzie mod oznacza jak zwykle resztę z dzielenia). Dla ciągu (bn) nie istnieje granica.

Intuicyjnie, gdyby g była granicą ciągu (bn), to musiałaby być jednocześnie blisko zera i blisko jedynki, bo 0 i 1 występują dowolnie daleko w tym ciągu. Wobec tego żadna liczba nie może spełniać definicji granicy dla ciągu (bn).
Intuicja nie zastąpi dowodu, więc spróbujmy zapisać to porządnie.
Załóżmy, że g jest granicą ciągu (bn). Ponieważ 0 i 1 są odległe o 1, to dowolna liczba rzeczywista g jest odległa od 0 lub 1 o przynajmniej \(\frac{1}{2}\). Wobec tego dla \(\epsilon < \frac{1}{2}\) definicja granicy nie powinna być spełniona dla żadnego \(g \in \mathbb{R}\). Sprawdźmy - weźmy \(\epsilon = \frac{1}{4}\). Ponieważ założyliśmy, że g jest granicą (bn), to istnieje n0 takie, że dla n > n0 zachodzą nierówności \(-\frac{1}{4} < b_n - g\) oraz \(b_n - g < \frac{1}{4}\).
Dla dowolnie wybranego \(n_0 \in \mathbb{N}\) istnieją wyrazy ciągu o indeksach n > n0 równe 0 i równe 1. Wobec tego powyższe nierówności muszą być spełnione, jeśli za bn podstawimy 0, jak również jesli podstawimy 1.
Podstawiając 0 otrzymujemy \(- \frac{1}{4} < g < \frac{1}{4}\), a podstawiając 1 dostajemy \(\frac{3}{4} < g < \frac{5}{4}\). Oczywiście nie istnieje liczba g, spełniająca wszystkie te nierówności - otrzymujemy sprzeczność.
Wobec tego dla \(\epsilon = \frac{1}{4}\) nie można dobrać n0 z definicji granicy, czyli granica nie istnieje. Zaprzeczyliśmy zdaniu "dla dowolnego ε istnieje n0 takie, że dla n > n0 wyrazy an są blisko g", wskazując wartość ε, równą \(\frac{1}{4}\), dla której to zadnie nie jest prawdziwe.
Warto zapamiętać wynikającą z tego przykładu intuicję: jeśli dany ciąg ma podciągi zbieżne do różnych granic, to nie może być zbieżny. Można również skonfrontować ten wniosek z problemem 3. z rozdziału o własnościach granic ciągów.
(b) Weźmy ciąg dn = n. Ten ciąg również nie ma granicy, ale można powiedzieć, że z innego powodu, niż poprzedni.
Ciąg dn jest rosnący, ale nie jest ograniczony. Jego wyrazy dążą do nieskończoności: to oznacza, że dla dowolnej liczby rzeczywistej K od pewnego momentu wyrazy ciągu są większe od K. Wobec tego żadna liczba g nie może być granicą ciągu (dn), ponieważ, niezależnie od wyboru ε, od pewnego momentu wyrazy ciągu będą większe niż g + ε, co jest sprzeczne z definicją granicy.
Do tego przykładu wrócimy, mówiąc o ciągach rozbieżnych do nieskończoności
Warto obliczyć kilka granic wprost z definicji, żeby się z nią oswoić. Oto kilka dobrych do tego przykładów - rezultaty na pewno przydadzą się w trudniejszych zadaniach, więc trzeba je zapamiętać.
Zadanie 1.
Znaleźć granicę ciągu \(a_n = \frac{n-1}{n}\).
Wobec tego wystarczy, jak w przykładzie 1, przyjąć za n0 dowolną liczbę naturalną większą od \(\frac{1}{\epsilon}\), co kończy dowód.
Zadanie 2.
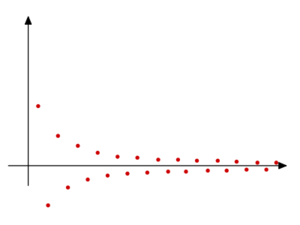
Znaleźć granicę ciągu \(a_n = \frac{(-1)^n}{n}\).
Zauważmy, że ciąg (an) zbiega do 0 z obu stron: wyrazy dla n parzystych są dodatnie, a wyznaczony przez nie podciąg jest malejący, natomiast wyrazy dla n nieparzystych tworzą podciąg rosnący, złożony z liczb ujemnych (jak na rysunku).
Zadanie 3.
Znaleźć granicę ciągu an = an, gdzie a jest pewną liczbą rzeczywistą.
Wiemy, że a < 1, więc \(\frac{1}{a} > 1\). Wobec tego dla pewnej liczby naturalnej k zachodzi nierówność \(\frac{1}{a} > 1 + \frac{1}{k}\). Wystarczy więc znaleźć n0 takie, że dla każdego n > n0 prawdziwa będzie nierówność \(\frac{1}{\epsilon} < (1 + \frac{1}{k})^n\).
Tu najłatwiej chyba skorzystać z nierówności Bernoulliego (zob. zadania z indukcji): \((1 +\frac{1}{k})^n \geq 1 + \frac{n}{k}\). Liczba po prawej stronie może być dowolnie duża - żeby była większa od \(\frac{1}{\epsilon}\), wystarczy wziąć \(n \geq k(\frac{1}{\epsilon} - 1)\). W szczególności wystarczy, żeby n0 spełniało tę nierówność. Wobec tego udało nam się dobrać n0 z definicji granicy do dowolnego ε, czyli udowodniliśmy, że 0 jest granicą ciągu an = an dla 0 < a < 1.
Oczywiście dla a = 1 ciąg (an) jest stale równy 1, a dla a = 0 jest stale równy 0. Dla a > 1 podobnymi technikami jak w powyższym dowodzie można uzasadnić, że ciąg (an) jest nieograniczony, więc nie jest zbieżny. Dla − 1 < a < 0 ciąg an jest zbieżny do 0, natomiast dla \(a \leq -1\) nie ma granicy (dowody podobne jak powyżej).
Zadanie 4.
Znaleźć granicę ciągu \(a_n = \sqrt[n]{a}\), gdzie a jest pewną liczbą rzeczywistą dodatnią.
Niech k będzie liczbą naturalną taką, że \(\frac{1}{k} \leq \epsilon\). Wówczas wystarczy, że odpowiednio duże n będą spełniały nierówność \(a < (1 + \frac{1}{k})^n\). Możemy zastosować nierówność Bernoulliego, jak w poprzednim zadaniu: \((1+ \frac{1}{k})^n \geq 1 + \frac{n}{k}\). Stąd dla n > k(a − 1) nierówność \(a < (1 + \frac{1}{k})^n\) będzie spełniona. W szczególności wystarczy wziąć za n0 dowolną liczbę naturalną większą niż k(a − 1).
W ten sposób wykazaliśmy, że granicą ciągu \(a_n = \sqrt[n]{a}\) dla \(a \geq 1\) jest 1. Analogicznymi metodami można udowodnić, że również dla 0 < a < 1 ciąg (an) jest zbieżny do 1. (Dla a = 0 oczywiście granicą jest 0, natomiast dla ujemnych a definicja ciągu nie ma sensu.)
Żeby umieć liczyć granice szybciej i łatwiej, niż korzystając za każdym razem z definicji, trzeba poznać kilka ogólnych własności pojęcia granicy.
