Własności granicy

pon., 09/13/2010 - 16:48 — ciebie

Na ciągach możemy wykonywać operacje arytmetyczne. Przypomnijmy, że mając dwa ciągi $(a n)$ i $(b n)$ możemy je dodawać, odejmować, mnożyć i pod pewnymi warunkami dzielić, wykonując te działania na kolejnych wyrazach ciągów (zobacz rozdział własności i operacje na ciągach). Załóżmy, że ciągi, na których wykonujemy działanie, są zbieżne. Czy wówczas istnieje granica ciągu $(c n)$ będącego ich sumą, różnicą, iloczynem lub ilorazem? Czy znając granice ciągów $(a n)$ i $(b n)$ , możemy obliczyć granicę ciągu $(c n)$ ? Odpowiedź jest zgodna z oczekiwaniami.

Twierdzenie 1:

Dane są ciągi liczbowe:  $(a n)$ , zbieżny do  $a$  i  $(b n)$ , zbieżny do  $b$ . Wówczas

1) ciąg $c n = a n + b n$ jest zbieżny do $a + b$ ,

2) ciąg $d n = - a n$ jest zbieżny do $- a$ ,

3) ciąg $e n = a n - b n$ jest zbieżny do $a - b$ ,

4) ciąg $f_n = a_n \cdot b_n$ jest zbieżny do $a b$ ,

5) jeśli dodatkowo wszystkie wyrazy ciągu $(b n)$ oraz jego granica $b$ są niezerowe, to ciąg $g_n = \frac{a_n}{b_n}$ jest zbieżny do $\frac{a}{b}$.

To twierdzenie bardzo ułatwia znajdowanie różnych granic: często ciąg dany skomplikowanym wzorem ogólnym można podzielić na dużo prostsze, połączone ze sobą za pomocą operacji arytmetycznych części, których granice łatwo jest obliczyć.

Zadanie 1.

Udowodnić punkt 2 twierdzenia 1.

To najłatwiejsza część tego twierdzenia. Wymaga tylko przyjrzenia się definicji granicy.

Problem 1.

Udowodnić pozostałe części twierdzenie 1.

Nie jest to bardzo trudne, ale trzeba dobrze zrozumieć definicję granicy i sprawnie nią operować. To zadanie jest dobrym ćwiczeniem dla osób, które na studiach zamierzają mieć coś wspólnego z matematyką. Rozwiązanie można znaleźć w każdym podręczniku analizy matematycznej, a także w niektórych podręcznikach szkolnych.

Przykład 1.

Zbadać zbieżność i znaleźć granicę ciągu $a_n = \frac{7n^2 - 4}{3(n+1)(n+2)}$.

Zacznijmy od przekształcenia wzoru ogólnego - dzielimy licznik i mianownik ułamka przez $n 2$ : $a_n = \frac{7 - 4n^{-1}}{3 + 3n^{-1} +2n^{-2}}$.

Ciąg $(a n)$ jest więc ilorazem ciągów $(b n)$ i $(c n)$ , gdzie $b n = 7 - 4 n - 1$ i $c n = 3 + 3 n - 1 + 2 n - 2$ .

Zajmijmy się najpierw ciągiem $(b n)$ : jest on sumą ciągów $b n' = 7$ i $b n'' = - 4 n - 1$ .

Wiemy, że $\lim_{n\rightarrow \infty} b_n' = 7$ oraz $\lim_{n\rightarrow \infty} b_n'' = \lim_{n\rightarrow \infty} (-4) \cdot \lim_{n\rightarrow \infty} n^{-1} = -4\cdot 0 = 0$. Wobec tego $\lim_{n\rightarrow \infty} b_n = 7+0 = 7$.

Ciąg $(c n)$ jest sumą ciągu stałego o wartości 3, ciągu $c n' = 3 n - 1$ i ciągu $c n'' = 2 n - 2$ . Granicą ciągu stałego jest oczywiście 3, ponadto $\lim_{n\rightarrow \infty} c_n' = 0$ oraz $\lim_{n\rightarrow \infty} c_n'' = 2\lim_{n\rightarrow \infty}\frac{1}{n^2} = 2(\lim_{n\rightarrow \infty}\frac{1}{n})(\lim_{n\rightarrow \infty}\frac{1}{n}) = 0$. (Czy umiesz uzasadnić wszstkie równości?)

Wobec tego $\lim_{n\rightarrow \infty} c_n = 3+0+0 = 3$.

Widzimy, że zarówno wszystkie wyrazy, jak i granica ciągu $(c n)$ są niezerowe, czyli możemy skorzystać z punktu 5 twierdzenia 1. Stąd, ponieważ ciągi $(b n)$ i $(c n)$ są zbieżne, to $(a n)$ również ma granicę, a ponadto $\lim_{n\rightarrow \infty} a_n = \frac{\lim_{n\rightarrow \infty} b_n}{\lim_{n\rightarrow \infty} c_n} = \frac{7}{3}$.

Ile razy skorzystaliśmy w tym rozumowaniu z twierdzenia 1?

Przyjrzyjmy się jeszcze raz przeskalowanemu wykresowi ciągu $a_n = \frac{1}{n}$.

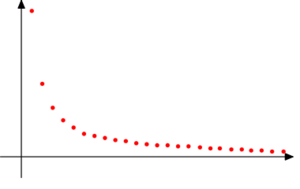
Ciąg jest malejący, a jego wyrazy są dodatnie. Kolejne liczby są coraz mniejsze i muszą się zmieścić pomiędzy zerem a wcześniejszymi wartościami. Wydaje się, że to jest powodem skupiania się wyrazów w pobliżu zera, czyli tego, że zero jest granicą ciągu $(a n)$ . Czy ta sytuacja jest szczególnym przypadkiem jakiejś ogólnej prawidłowości?

Intuicja

Przyjmijmy, że ciąg jest monotoniczny, czyli konsekwentnie idzie do góry lub do dołu, ewentualnie zatrzymując się czasami, oraz jest ograniczony, czyli wszystkie jego wyrazy leżą między dwiema prostymi. Wtedy odstępy między kolejnymi wyrazami nie mogą być duże - muszą dążyć do zera, żeby ciąg nie wyszedł poza ograniczające go proste. Wobec tego dla dużych $n$ wyrazy ciągu są bardzo blisko siebie. Stąd wynika, że muszą leżeć również bardzo blisko pewnej prostej, czyli nasz ciąg ma granicę.

To rozumowanie jest mało precyzyjne, ale okazuje się, że następujące twierdzenie jest prawdziwe:

Twierdzenie 2:

Jeśli ciąg  $(a n)$  jest monotoniczny i ograniczony, to jest zbieżny.

Uwaga: W twierdzeniu wystarczy, żeby ciąg $(a n)$ był rosnący i ograniczony z góry lub malejący i ograniczony z dołu - dlaczego?

To twierdzenie pozwala nam często łatwo stwierdzić, że pewien ciąg jest zbieżny, ale nie pomaga poznać jego granicy. Mimo to jest bardzo użyteczne.

Przykład 2.

Udowodnimy, że ciąg $a_n = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \ldots + \frac{1}{n^2}$ jest zbieżny.

Zauważmy, że $a n + 1$ otrzymujemy, dodając do $a n$ składnik $\frac{1}{(n+1)^2}$, który jest dodatni. Wobec tego ciąg $(a n)$ jest rosnący.

Żeby wykazać, że ciąg $(a n)$ jest ograniczony, skorzystamy z nierówności $\frac{1}{n^2} \leq \frac{1}{n-1} - \frac{1}{n}$ (dla $n > 1$ ), którą można udowodnić przez proste przekształcenia. Zapiszmy $a_n = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \ldots \frac{1}{(n-1)^2} + \frac{1}{n^2} \leq 1 + 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \ldots + \frac{1}{n-2} - \frac{1}{n-1} + \frac{1}{n-1} - \frac{1}{n} = 2 - \frac{1}{n}$, gdzie ostatnią równość otrzymujemy zauważając, że sąsiednie składniki sumy się redukują. Stąd wynika, że każdy wyraz ciągu $(a n)$ jest mniejszy od 2, czyli ciąg jest ograniczony z góry przez 2.

Wobec tego z twierdzenia 2 ciąg $(a n)$ jest zbieżny. Ale jaka jest jego granica? Wcale nie tak łatwo ją znaleźć - okazuje się, że jest to $\frac{\pi^2}{6}$ :-)

Przykład 3.

Korzystając z twierdzenia 2 można również wykazać zbieżność ciągu $a_n = (1 + \frac{1}{n})^n$. Jego granicą jest $e$ - liczba Eulera.

Przyjmijmy, że ciągi $(a n)$ i $(b n)$ są zbieżne do tej samej liczby $g$ , a ponadto dla wszystkich $n \in \mathbb{N}$ zachodzą nierówności $a_n \leq b_n$. Załóżmy, że wyrazy ciągu $(c n)$ dla każdego $n \in \mathbb{N}$ spełniają nierówności $a_n \leq c_n \leq b_n$. Czyli ciąg $(c n)$ musi się zmieścić pomiędzy $(a n)$ i $(b n)$ . Co można w tej sytuacji powiedzieć o granicy ciągu $(c n)$ ?

Twierdzenie 3:

(O trzech ciągach)

Załóżmy, ciągi $(a n)$ i $(b n)$ są zbieżne do $g$ , a ponadto wyrazy tych ciągów i ciągu $(c n)$ dla każdego $n \in \mathbb{N}$ spełniają nierówności $a_n \leq b_n \leq c_n$. Wówczas ciąg $(c n)$ jest zbieżny do $g$ .

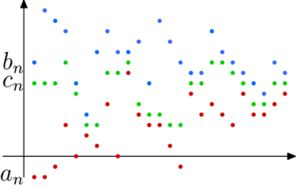
Intuicyjnie, ponieważ wyrazy $(a n)$ i $(b n)$ od pewnego miejsca są blisko $g$ , a wyrazy $(c n)$ są pomiędzy nimi, to również leżą blisko $g$ . To rozumowanie można bardzo łatwo przetłumaczyć na precyzyjny dowód.

Przykład 4.

Wykażemy, że ciąg $c_n = \sqrt[n]{5^{n} + (-3)^n}$ jest zbieżny i znajdziemy jego granicę.

W tym celu skonstruujemy ciągi $(a n)$ i $(b n)$ , ograniczające ciąg $(c n)$ z dołu i z góry, jak w twierdzeniu 3. Kluczową własnością, którą musimy zapewnić jest to, że ciągi $(a n)$ i $(b n)$ będą zbieżne do tej samej liczby.

Weźmiemy $a_n = \sqrt[n]{5^{n-1}}$ oraz $b_n = \sqrt[n]{2\cdot 5^n}$.

Zaczniemy od wykazania nierówności $a_n \leq c_n$, czyli $\sqrt[n]{5^{n-1}} \leq \sqrt[n]{5^n + (-3)^n}$.

Jest ona równoważna $5^{n-1} \leq 5\cdot 5^{n-1} + (-3)^n$, czyli $4\cdot 5^{n-1} + (-3)^ \geq 0$.

Wystarczy więc wykazać, że $4\cdot 5^{n-1} \geq |(-3)^n| = 3^n$. A to jest prawdą dla dowolnego $n \in \mathbb{N}$, ponieważ $4 > 3$ i $5 n - 1 > 3 n - 1$ .

Jeszcze łatwiej można dowieść nierówności $c_n \leq b_n$: $5^n + (-3)^n \leq 5^n + 3^n \leq 5^n + 5^n = 2\cdot 5^n$, a stąd wynika nierówność między pierwiastkami z tych wyrażeń.

Sprawdźmy, czy granice istnieją i się zgadzają. Dla ciągu $a n$ :

$\lim_{n \rightarrow \infty} a_n = \lim_{n \rightarrow \infty} \sqrt[n]{5^{n-1}} = \lim_{n \rightarrow \infty} \sqrt[n]{\frac{1}{5}\cdot 5^n} = 5 \lim_{n \rightarrow \infty} \sqrt[n]{\frac{1}{5}} = 5 \cdot 1 = 5$.

Dla ciągu $b n$ obliczenia są podobne:

$\lim_{n \rightarrow \infty} b_n = \lim_{n \rightarrow \infty} \sqrt[n]{2\cdot 5^n} = 5\lim_{n \rightarrow \infty} \sqrt[n]{5} = 5 = \lim_{n \rightarrow \infty} a_n$.

Możemy więc skorzystać z twierdzenia o trzech ciągach - ciąg $c n$ jest zbieżny do $g = 5$ .

Kilka innych własności granic ciągów pozostawiamy w formie problemów do samodzielnego przemyślenia. Można je też po prostu te twierdzenia zapamiętać i korzystać z nich w rozwiązywaniu zadań.

Problem 2.

Wykazać, że jeśli ciąg $(a n)$ jest zbieżny, to jest ograniczony.

Rozwiązanie:

Musimy jeszcze uwzględnić wyrazy ciągu $a n$ o indeksach nie większych niż $n 0$ . Jest ich skończenie wiele, więc na pewno możemy powiedzieć, który jest największy - niech będzie to $a i$ , oraz który jest najmniejszy - oznaczmy go $a j$ .

Liczba $m a x (a i, g + ε)$ jest graniczeniem górnym ciągu $a n$ , natomiast $m i n (a j, g + ε)$ jest ograniczeniem dolnym tego ciągu.

Problem 3.

Wykazać, że ciąg $(a n)$ jest zbieżny do granicy $g$ wtedy i tylko wtedy, gdy każdy jego podciąg jest zbieżny do $g$ .

Szkic rozwiązania:

W drugą stronę, jeśli $g$ jest granicą ciągu $(a n)$ , to dla dowolnego $ε > 0$ możemy dobrać $n 0$ tak, żeby warunek z definicji był spełniony. Wystarczy sprawdzić, że dla dowolnego podciągu $(b m)$ ciągu $(a n)$ tak samo dobrane $n 0$ spełnia warunek z definicji granicy, a stąd $g$ jest granicą $(b m)$ .

Stąd wynika, że wystarczy wskazać w danym ciągu dwa podciągi zbieżne do różnych granic, żeby wykazać, że ten ciąg nie jest zbieżny. Na przykład w ciągu $a_n = n \mod 2$ podciąg złożony z wyrazów o numerach nieparzystych, $b m = a 2 m - 1$ , zawiera same jedynki, więc jego granicą jest 1, a podciąg $c m = a 2 m$ składa się z samych zer, więc jego granicą jest 0. Stąd ciąg $(a n)$ nie ma granicy.

Inny ciekawy wniosek jest taki, że badając zbieżność pewnego ciągu, możemy "obciąć" jego początek, czyli zajmować się podciągiem $b n = a k + n$ dla pewnej liczby naturalnej $k$ .

Problem 4. (Twierdzenie Bolzano - Weierstrassa)

Udowodnić, że każdy ciąg ograniczony ma podciąg zbieżny.

Szkic rozwiązania:

1. dodajemy do podciągu dowolny wyraz ciągu $(a n)$ ; dzielimy odcinek $[A, B]$ na pół - przynajmniej w jednej połowie jest nieskończenie wiele wyrazów ciągu $(a n)$ ; wybieramy połowę spełniającą ten warunek i oznaczamy jej końce przez $A 1$ i $B 1$ ;

2. dodajemy do podciągu dowolny wyraz ciągu $(a n)$ , o indeksie większym, niż ten wybrany poprzednio i leżący w odcinku $[A 1, B 1]$ ; konstruujemy odcinek $[A 2, B 2]$ , biorąc połowę odcinka $[A 1, B 1]$ zawierającą nieskończenie wiele wyrazów ciągu $(a n)$ ;

$\infty$. powtarzamy nieskończenie wiele czynności jak w punkcie 2, dodając do ciągu $(b m)$ wyrazy $(a n)$ , leżące w kolejno konstruowanych odcinkach $[A i, B i]$ .

Dlaczego tak skonstruowany ciąg $(b m)$ jest podciągiem $(a n)$ ?

Jak uzasadnić, że ciąg $(b m)$ jest zbieżny?

Wskazówka: Wyrazy ciągu $(b m)$ dla $m > i$ leżą w odcinku $[A i, B i]$ . Jaką długość mają odcinki $[A i, B i]$ ? Jak zachowuje się ciąg długości tych odcinków?

Theme by Dr. Radut.

Własności granicy

dla autorów