Ponieważ przeprowadzania dowodów indukcyjnych najłatwiej się nauczyć, oglądając przykłady, zobaczmy kilka porządnie opisanych przykładów.
Udowodnić, że dla dowolnej liczby naturalnej n liczba 11n + 1 + 122n − 1 jest podzielna przez 133.
Rozwiązanie
Liczba naturalna jest podzielna przez 133 wtedy i tylko wtedy, gdy można ją zapisać jako iloczyn \(133\cdot k\), gdzie k jest liczbą naturalną. Wobec tego chcemy udowodnić, że dla dowolnego \(n \in \mathbb{N}\) istnieje \(k \in \mathbb{N}\) takie, że 11n + 1 + 122n − 1 = 133k.
Dowodzimy przez indukcję.
1. Sprawdzamy dla n = 1: \(11^2 + 12 = 121 + 12 = 133 = 133\cdot 1\).
2. Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1.
Zauważmy, że \(11^{(n+1) + 1} + 12^{2(n+1) - 1} = 11\cdot 11^{n+1} + 12^2 \cdot 12^{2n-1} = 11\cdot 11^{n+1} + (133 + 11) \cdot 12^{2n-1} = 11\cdot (11^{n+1} + 12^{2n-1}) + 133\cdot 12^{2n-1}\).
Korzystamy z założenia indukcyjnego: istnieje liczba naturalna k taka, że 11n + 1 + 122n − 1 = 133k.
Wobec tego powyższe wyrażenie jest równe \(11\cdot 133\cdot k + 133\cdot 12^{2n-1} = 133\cdot (11k + 12^{2n-1})\), czyli jego wartość jest podzielna przez 133 (ponieważ wartość wyrażenia w nawiasie jest liczbą całkowitą).
Na mocy zasady indukcji matematycznej teza zadania jest prawdziwa dla dowolnego \(n \in \mathbb{N}\).
Dla jakich \(n \in \mathbb{N}\) zachodzi nierówność 3n > n3?
Rozwiązanie
Rowiązywanie zadań, w których treść wymaga znalezienia wszystkich wartości, dla których pewien warunek jest spełniony, warto rozpoczynać od zbadania zachowania tego warunku dla niedużych wartości. Wobec tego sprawdzamy daną nierówność dla małych n.
n = 1: 31 > 13 - zgadza się;
n = 2: 32 = 9 > 23 = 8 - zgadza się;
n = 3: po obu stronach mamy 33 = 27 - jest równość zamiast ostrej nierówności, czyli dla 3 nierówność nie jest spełniona;
n = 4: 34 = 81 > 43 = 64;
n = 5: 35 = 243 > 53 = 125...
Można się spodziewać, że dla większych wartości n lewa strona nierówności będzie rosła dużo szybciej niż prawa, więc nierówność będzie spełniona. Ale trzeba to udowodnić!
Przeprowadzimy dowód indukcyjny.
1. Zaczniemy indukcję od n = 4, ponieważ dla mniejszych liczb nierówność nie zawsze jest spełniona.
2. Załóżmy, że udowodniliśmy tę nierówność dla liczb od 4 do n, dowodzimy dla n + 1.
Chcemy wykazać, że 3n + 1 > (n + 1)3. Zapisujemy 3n + 1 jako \(3\cdot 3^n\) i korzystamy z założenia indukcyjnego, otrzymując \(3\cdot 3^n > 3\cdot n^3\).
Żeby wykazać tezę dla n + 1, wystarczy więc udowodnić nierówność 3n3 > (n + 1)3, czyli 3n3 > n3 + 3n2 + 3n + 1, co jest równoważne 2n3 > 3n2 + 3n + 1 (1).
Zauważmy, że jeśli n > 3, to n3 > 3n2 oraz n3 > 3n + 1 (ponieważ \(n^3 - 3n = n(n^2-3) \geq n\cdot 1 > 1\)).
Sumując stronami te dwie nierówności otrzymujemy nierówność (1), co kończy dowód kroku indukcyjnego.
Na mocy zasady indukcji matematycznej nierówność 3n > n3 jest prawdziwa dla wszystkich liczb naturalnych \(n\geq 4\). Ponadto z bezpośredniego sprawdzenia wynika, że ta nierówność jest spełniona również dla n = 1 i n = 2, natomiast nie zachodzi dla n = 3.
Wykazać, że n-kąt wpisany w okrąg ma \(\frac{n(n-3)}{2}\) przekątnych.
Uwaga: Do czego potrzebne jest założenie, że wielokąt ma być wpisany w okrąg? Wielokąt spełniający ten warunek ma dobre własności. Nie mogą się w nim zdarzyć dziwne sytuacje, np. takie, że przekątna wychodzi poza wnętrze wielokąta, czy że pewne przekątne częściowo się pokrywają. Można tutaj z pewnością wypisać słabsze założenia, ale nie chodzi nam o to, żeby sprawdzić, jak bardzo ogólny jest ten wzór, ale żeby zobaczyć, jak opisać liczbę przekątnych w przypadku porządnych wielokątów.
Rozwiązanie
Zastosujemy zasadę indukcji matematycznej.
1. Sensowny początek indukcji to n = 3 - trudno określić, czym miałby być wielokąt o jednym lub dwóch wierzchołkach i bokach. Dla n = 3 we wzorze mamy \(\frac{3(3-3)}{2} = 0\), czyli liczbę przekątnych trójkąta.
2. Załóżmy, że wykazaliśmy tezę dla liczb od 3 do n, dowodzimy dla n + 1.
Wybierzmy trzy kolejne wierzchołki n + 1-kąta. Oznaczmy je A, B i C, jak na rysunku. Rysując przekątną łączącą A i C odcinamy od wielokąta trójkąt ABC. Otrzymujemy w ten sposób n-kąt wpisany w okrąg. Z założenia indukcyjnego liczba przekątnych w tym n-kącie wynosi \(\frac{n(n-3)}{2}\) - oczywiście wszystkie te przekątne są również przekątnymi wyjściowego n + 1-kąta.
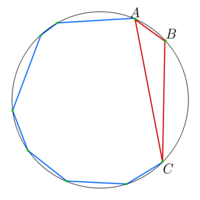
Musimy się tylko zastanowić, ile przekątnych straciliśmy, odcinając trójkąt ABC. Są to przekątne wychodzące z wierzchołka B oraz odcinek AC. Drugim końcem przekątnej wychodzącej z punktu B może być dowolny wierzchołek n + 1-kąta poza A, B i C (dla A i C zamiast przekątnych otrzymalibyśmy boki). Takich wierzchołków jest n + 1 − 3 = n − 2, więc jeszcze nie policzonych przekątnych jest n − 1.
Wobec tego wszystkich przekątnych n + 1-kąta jest \(\frac{n(n-3)}{2} + n-1 = \frac{n^2-3n+2n-2}{2} = \frac{n^2-n -2}{2} = \frac{(n+1)(n-2)}{2}\), co należało udowodnić.
Na mocy zasady indukcji matematycznej teza twierdzenia jest prawdziwa dla dowolnego \(n \in \mathbb{N}\), \(n \geq 3\).
Rozwiązanie drugie, nieindukcyjne.
Policzmy najpierw przekątne wychodzące z wybranego wierzchołka A. Drugim końcem takiej przekątnej może być dowolny wierzchołek n-kąta oprócz A i jego dwóch sąsiadów, czyli z każdego wierzchołka wychodzą n − 3 przekątne. Mnożąc tę liczbę przez liczbę wierzchołków wielokąta każdą przekątną policzymy dwa razy - raz dla każdego jej końca. Wobec tego liczba wszystkich przekątnych to połowa tego, co otrzymamy, zliczając dla wszystkich wierzchołków wychodzące z nich przekątne, czyli \(\frac{n(n-3)}{2}\).
To rozwiązanie jest od poprzedniego istotnie krótsze w zapisie, ale żeby je napisać, najpierw trzeba mieć pomysł. Rozwiązania indukcyjne często wymagają mniej pomysłowości, ale za to nieco więcej rachunków.
Udowodnić, że dla każdej liczby naturalnej n zachodzi nierówność:
\(\frac{1}{n+1} + \frac{1}{n+2} + \ldots + \frac{1}{3n+1} \geq 1\).
Rozwiązanie
Prowadzimy dowód przez indukcję względem n.
1. Sprawdźmy nierówność dla n = 1: \(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{13}{12} \geq 1\)
2. Załóżmy, że udowodniliśmy daną nierówność dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Lewa strona to \(\frac{1}{(n+1) + 1} + \frac{1}{(n+1)+2} + \ldots + \frac{1}{3(n+1) + 1} = \frac{1}{n+2} + \frac{1}{n+3} + \ldots + \frac{1}{3n+4}\).
Ta suma jest bardzo podobna do sumy z lewej strony nierówności dla n - różnią się one tylko o kilka wyrazów. Dokładniej, jeśli przez Lk oznaczymy lewą stronę nierówności dla n = k, to \(L_{n+1} = L_n -\frac{1}{n+1} + \frac{1}{3n+2} + \frac{1}{3n+3} + \frac{1}{3n+4} \geq 1 -\frac{1}{n+1} + \frac{1}{3n+2} + \frac{1}{3n+3} + \frac{1}{3n+4}\), gdzie nierówność otrzymujemy korzystając z założenia indukcyjnego.
Wobec tego żeby udowodnić, że \(L_{n+1} \geq 1\), wystarczy wykazać, że \(1 -\frac{1}{n+1} + \frac{1}{3n+2} + \frac{1}{3n+3} + \frac{1}{3n+4} \geq 1\). Ta nierówność jest równoważna \(\frac{1}{3n+2} + \frac{1}{3n+3} + \frac{1}{3n+4} \geq \frac{1}{n+1}\).
Wykonując dodawanie przekształcamy ją do postaci \(\frac{27n^2+ 54n + 26}{(3n+2)(3n+3)(3n+4)} \geq \frac{1}{n+1}\)
i dalej \(\frac{27n^2+ 54n + 26}{3(3n+2)(3n+4)} \geq 1\),
czyli równoważnie \(27n^2+ 54n + 26 \geq 3(3n+2)(3n+4)\).
Rozwijając prawą stronę otrzymujemy \(27n^2+ 54n + 26 \geq 27n^2 + 54n + 24\), a ta nierówność jest prawdziwa dla każdej liczby naturalnej n, co na mocy zasady indukcji matematycznej dowodzi tezy.
Z dowodami indukcyjnymi trzeba czasami uważać - może się zdarzyć, że pominiemy jakiś ważny szczególny przypadek, przez co cały dowód okaże się błędny...
"Twierdzenie": Wszystkie koty są tego samego koloru. (W tym twierdzeniu przenosimy się do świata, gdzie koty są jednokolorowe.)
"Dowód": Wystarczy wykazać, że w dowolnym zbiorze zawierającym n kotów, gdzie n jest dowolną liczbą naturalną, wszystkie koty mają ten sam kolor.
1) Podstawa indukcji to sprawdzenie dla n = 1: oczywiście w zbiorze zawierającym tylko jednego kota wszystkie koty są tego samego koloru.
2) Załóżmy, że udowodniliśmy twierdzenie dla wszystkich liczb naturalnych od 1 do n − 1, dowodzimy dla n. Weźmy dowolny zbiór A zawierający n kotów. Pokażemy, że koty ze zbioru A są tego samego koloru.
Wyrzucając z A pewnego kota X otrzymamy zbiór zawierający n − 1 kotów - możemy skorzystać z założenia indukcyjnego, żeby stwierdzić, że wszystkie koty w A oprócz X mają ten sam kolor. Ale teraz, wyrzucając z A kota Y (innego niż X), wnioskujemy z założenia indukcyjnego, że kot X ma ten sam kolor, co pozostałe koty w A. Wobec tego wszystkie koty w A mają ten sam kolor.
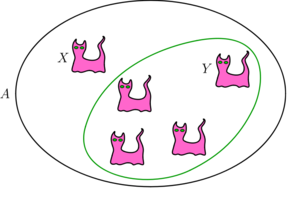
Zatem na mocy zasady indukcji matematycznej wszystkie koty są tego samego koloru.
Podczas dowodu zapewne większość osób wyobraża sobie zbiór A większy niż dwuelementowy (jak na rysunku). Dla takiego zbioru rozumowanie z kroku indukcyjnego jest poprawne, ale nic z tego nie wynika, bo nie działa ono dla n = 2. Wobec tego nie mamy podstawy do stosowania indukcji. Umiemy sprawdzić przypadek n = 1, a krok indukcyjny działa dopiero od n = 3 - przerwa pomiędzy tymi wartościami powoduje, że dowód jest zupełnie bez sensu.
