Wskazówką do wszystkich zadań jest zasada indukcji.
Przedstawione zostały rozwiązania oparte na indukcji. Ponieważ naszym celem jest wyjaśnienie rozumowania, pomijamy w opisie sformułowania w rodzaju przeprowadzimy dowód indukcyjny lub na mocy zasady indukcji teza jest prawdziwa, ale zaznaczamy, że w dokładnym i porządnym opisie rozwiązania powinny się one znaleźć.
Warto również poszukiwać rozwiązań innych niż indukcyjne!
Zadanie 1.
Udowodnić, że dla dowolnej liczby naturalnej n zachodzi wzór \(1\cdot 2 + 2\cdot 3 + 3\cdot 4 + \ldots + n(n+1) = \frac{1}{3}n(n+1)(n+2)\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(1\cdot 2 + 2\cdot 3 + 3\cdot 4 + \ldots + n(n+1) = \frac{1}{3}n(n+1)(n+2) + (n+1)(n+2) = (n+1)(n+2)(\frac{1}{3}n + 1) = \frac{1}{3}(n+1)(n+2)(n+3)\),
co należało udowodnić.
Zadanie 2.
Udowodnić, że dla dowolnej liczby naturalnej n zachodzi wzór \(1\cdot 2 \cdot 3 + 2\cdot 3 \cdot 4 + 3\cdot 4 \cdot 5 + \ldots + n(n+1)(n+2) = \frac{1}{4}n(n+1)(n+2)(n+3)\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(1\cdot 2 \cdot 3 + 2\cdot 3 \cdot 4 + 3\cdot 4 \cdot 5 + \ldots + n(n+1)(n+2) + (n+1)(n+2)(n+3) = \frac{1}{4}n(n+1)(n+2)(n+3) + (n+1)(n+2)(n+3) =\) \( =(n+1)(n+2)(n+3)(\frac{1}{4}n + 1) = \frac{1}{4}(n+1)(n+2)(n+3)(n+4) \),
co należało udowodnić.
Zadanie 3.
Udowodnić, że dla dowolnej liczby naturalnej n zachodzi wzór \(1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(1^2 + 2^2 + 3^2 + \ldots + n^2 + (n+1)^2 = \frac{n(n+1)(2n+1)}{6} + (n+1)^2 = \frac{1}{6}(n+1)(n(2n+1) + 6(n+1)) =\) \(= \frac{1}{6}(n+1)(2n^2 + 7n + 6) = \frac{1}{6}(n+1)(2n+3)(n+2) = \frac{(n+1)(n+2)(2(n+1) + 1)}{6}\),
co należało udowodnić.
Zadanie 4.
Udowodnić, że dla dowolnej liczby naturalnej n zachodzi wzór \(1^3 + 2^3 + 3^3 + \ldots + n^3 = (\frac{n(n+1)}{2})^2\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(1^3 + 2^3 + 3^3 + \ldots + n^3 + (n+1)^3 = (\frac{n(n+1)}{2})^2 + (n+1)^3 = (n+1)^2(\frac{n^2}{4} + n+1) =\) \( = (n+1)^2(\frac{n^2 + 4n + 4}{4}) = (n+1)^2(\frac{(n+2)^2}{4}) = (\frac{(n+1)(n+2)}{2})^2\),
co należało udowodnić.
Zadanie 5.
Udowodnić, że dla każdej liczby naturalnej \(n \geq 2\) zachodzi nierówność \(\frac{1}{\sqrt{1}} + \frac{1}{\sqrt{2}}+ \ldots + \frac{1}{\sqrt{n}} > \sqrt{n}.\)
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając z założenia indukcyjnego otrzymujemy nierówność \(\frac{1}{\sqrt{1}} + \frac{1}{\sqrt{2}}+ \ldots + \frac{1}{\sqrt{n}} + \frac{1}{\sqrt{n+1}} > \sqrt{n} + \frac{1}{\sqrt{n+1}} = \frac{\sqrt{n(n+1)}+1}{\sqrt{n+1}}\).
Wystarczy więc wykazać, że \(\frac{\sqrt{n(n+1)}+1}{\sqrt{n+1}} > \sqrt{n+1}\).
Mnożąc tę nierówność stronami przez \(\sqrt{n+1}\) otrzymujemy równoważną postać \(\sqrt{n(n+1)} + 1 > (\sqrt{n+1})^2\)
i dalej \(\sqrt{n(n+1)} > n+1 -1 = n\),
co jest prawdą, ponieważ \(\sqrt{n(n+1)} > \sqrt{n\cdot n} = n\).
Zadanie 6.
Udowodnić, że dla każdej liczby naturalnej n zachodzi nierówność \(\frac{1}{\sqrt{1}} + \frac{1}{\sqrt{2}}+ \ldots + \frac{1}{\sqrt{n}} < 2\sqrt{n}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając z założenia indukcyjnego, otrzymujemy nierówność \( \frac{1}{\sqrt{1}} + \frac{1}{\sqrt{2}}+ \ldots + \frac{1}{\sqrt{n}} + \frac{1}{\sqrt{n+1}} < 2\sqrt{n} + \frac{1}{\sqrt{n+1}} = \frac{2\sqrt{n(n+1)} + 1}{\sqrt{n+1}}\).
Wystarczy więc wykazać, że \(\frac{2\sqrt{n(n+1)}+1}{\sqrt{n+1}} < 2\sqrt{n+1}\).
Mnożąc tę nierówność stronami przez \(\sqrt{n+1}\) otrzymujemy równoważną postać \(2\sqrt{n(n+1)} + 1 < 2(\sqrt{n+1})^2\)
i dalej \(\sqrt{n(n+1)} < \frac{1}{2}(2n+2 -1) = n+\frac{1}{2}\).
Obie strony nierówności są dodatnie, więc możemy przejść do równoważnej postaci, podnosząc nierówność stronami do kwadratu. Otrzymana nierówność \(n(n+1) > (n+\frac{1}{2})^2 = n^2 + n + \frac{1}{4}\) oczywiście jest prawdziwa.
Zadanie 7.
Wykazać, że \(\frac{1}{1\cdot 2} + \frac{1}{2\cdot 3} + \ldots + \frac{1}{n(n+1)} = 1 - \frac{1}{n+1}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(\frac{1}{1\cdot 2} + \frac{1}{2\cdot 3} + \ldots + \frac{1}{n(n+1)} + \frac{1}{(n+1)(n+2)} = 1 - \frac{1}{n+1} + \frac{1}{(n+1)(n+2)} =\)
\( = 1 - \frac{1}{n+1}(1 - \frac{1}{n+2}) = 1 - \frac{1}{n+1}\cdot \frac{n+1}{n+2} = 1 - \frac{1}{n+2}\),
co należało udowodnić.
Zadanie 8.
Wykazać, że dla dowolnej liczby naturalnej n zachodzi wzór \(\frac{1}{1\cdot 2\cdot 3} + \frac{1}{2\cdot 3\cdot 4} + \ldots + \frac{1}{n(n+1)(n+2)} = \frac{1}{4} - \frac{1}{2(n+1)(n+2)}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(\frac{1}{1\cdot 2\cdot 3} + \frac{1}{2\cdot 3\cdot 4} + \ldots + \frac{1}{n(n+1)(n+2)} + \frac{1}{(n+1)(n+2)(n+3)}= \frac{1}{4} - \frac{1}{2(n+1)(n+2)} + \frac{1}{(n+1)(n+2)(n+3)} =\)
\( = \frac{1}{4} - \frac{1}{(n+1)(n+2)}(\frac{1}{2} - \frac{1}{n+3}) = \frac{1}{4} - \frac{1}{(n+1)(n+2)}\cdot \frac{n+3-2}{2(n+3)} = \frac{1}{4} - \frac{1}{2(n+2)(n+3)}\),
co należało udowodnić.
Zadanie 9.
Wykazać, że dla dowolnej liczby naturalnej \(n \geq 2\) zachodzi wzór \((1 - \frac{1}{4})(1 - \frac{1}{9})\cdots (1 - \frac{1}{n^2}) = \frac{n+1}{2n}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\((1 - \frac{1}{4})(1 - \frac{1}{9})\cdots (1 - \frac{1}{n^2})(1-\frac{1}{(n+1)^2}) = \frac{n+1}{2n}\cdot (1-\frac{1}{(n+1)^2}) = \frac{n+1}{2n} - \frac{1}{2n(n+1)} = \)
\( = \frac{(n+1)^2 - 1}{2n(n+1)} = \frac{n^2 + 2n}{2n(n+1)} = \frac{n(n+2)}{2n(n+1)} = \frac{n+2}{2(n+1)}\),
co należało udowodnić.
Zadanie 10.
Udowodnić, że dla dowolnej liczby naturalnej n zachodzi wzór \(\frac{1}{5 \cdot 8} + \frac{1}{8 \cdot 11} + \ldots + \frac{1}{[5+3(n-1)](5+3n)} = \frac{n}{5 \cdot (5+3n)}\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając na początku z założenia indukcyjnego, otrzymujemy ciąg równości:
\(\frac{1}{5 \cdot 8} + \frac{1}{8 \cdot 11} + \ldots + \frac{1}{[5+3(n-1)](5+3n)} + \frac{1}{(5 + 3n)[5+3(n+1)]} = \frac{n}{5 \cdot (5+3n)} + \frac{1}{(5 + 3n)[5+3(n+1)]} =\)
\( = \frac{1}{5+3n}(\frac{n}{5} + \frac{1}{8+3n}) = \frac{1}{5+3n}\cdot \frac{n(8+3n) + 5}{5(8+3n)} = \frac{1}{5+3n}(\frac{3n^2 + 8n + 5}{5(8+3n)}) = \frac{1}{3n+5}(\frac{(3n+5)(n+1)}{5(8+3n)}) = \frac{n+1}{5[5+3(n+1)]}\),
co należało udowodnić.
Zadanie 11.
Udowodnić, że dla dowolnej liczby naturalnej n liczba n3 + 2n jest podzielna przez 3.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Zauważmy, że (n + 1)3 + 2(n + 1) = n3 + 3n2 + 3n + 1 + 2n + 2 = n3 + 2n + 3(n2 + n + 1). Z założenia indukcyjnego liczba n3 + 2n jest podzielna przez 3, więc również (n + 1)3 + 2(n + 1) jest liczbą podzielną przez 3, jako suma dwóch liczb podzielnych przez 3.
Zadanie 12.
Udowodnić, że dla dowolnej liczby naturalnej n liczba 34n + 2 + 1 jest podzielna przez 10.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Zauważmy, że
\(3^{4(n+1)+2} + 1 = 3^{(4n+2) + 4} + 1 = 3^4\cdot 3^{4n+2} + 1 = 3^4 \cdot 3^{4n+2} + 3^4 - 3^4 + 1 = 3^4(3^{4n+2} + 1) - 80\).
Z założenia indukcyjnego liczba 34n + 2 + 1 jest podzielna przez 10, więc również 34(34n + 2 + 1) jest liczbą podzielną przez 10. Zapisaliśmy 34(n + 1) + 2 + 1 jako różnicę dwóch liczb podzielnych przez 10, więc ta liczba musi być podzielna przez 10.
Zadanie 13.
Udowodnić, że dla dowolnej liczby naturalnej n liczba 10n − 4 jest podzielna przez 6.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Zauważmy, że
\(10^{n+1} - 4 = 10\cdot 10^n - 4 = 10 \cdot 10^n - 40 + 40 - 4 = 10(10^n - 4) + 36\).
Z założenia indukcyjnego liczba 10n − 4 jest podzielna przez 6, więc również 10(10n − 4) jest liczbą podzielną przez 6. Zapisaliśmy 10n + 1 − 4 jako sumę dwóch liczb podzielnych przez 6, więc jest to liczba podzielna przez 6.
Zadanie 14.
Udowodnić, że dla dowolnej liczby naturalnej n liczba n3 − n jest podzielna przez 6.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Zauważmy, że (n + 1)3 − (n + 1) = n3 + 3n2 + 3n + 1 − n − 1 = n3 − n + 3n(n + 1). Z założenia indukcyjnego liczba n3 − n jest podzielna przez 6. Wobec tego wystarczy wykazać, że dla dowolnej liczby naturalnej n liczba 3n(n + 1) jest podzielna przez 6. Wiemy, że ta liczba jest podzielna przez 3. Ponadto musi być parzysta, ponieważ albo n, albo n + 1 jest liczbą parzystą, więc ich iloczyn jest parzysty. Wobec tego 3n(n + 1) jest podzielna przez 2 i przez 3, więc również przez 6. Stąd teza zadania.
Zadanie 15.
Udowodnić, że dla dowolnej liczby naturalnej n liczba \(10^{3n+1} - 3\cdot (-1)^n\) jest podzielna przez 7.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Zauważmy, że
\(10^{3(n+1) + 1} - 3\cdot (-1)^{n+1} = 10^3\cdot 10^{3n+1} -10^3\cdot 3 \cdot (-1)^n + 10^3\cdot 3 \cdot (-1)^n - 3\cdot (-1)^{n+1}=\)
\(= 10^3(10^{3n+1} - 3\cdot (-1)^n) + 3\cdot (-1)^n\cdot (10^3 + 1) = 10^3(10^{3n+1} - 3\cdot (-1)^n) + 3\cdot (-1)^n\cdot 1001 \).
Z założenia indukcyjnego pierwszy składnik sumy jest podzielny przez 7. Natomiast drugi składnik jest iloczynem 1001 i pewnej liczby całkowitej, a \(1001 = 7 \cdot 11\cdot 13\), więc drugi składnik sumy także jest podzielny przez 7. Wobec tego również suma jest podzielna przez 7, co należało udowodnić.
Zadanie 16.
Udowodnić, że dla dowolnej liczby naturalnej n liczba \(2^{4^n}+5\) jest podzielna przez 21.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Z założenia indukcyjnego liczba \(2^{4^n} + 5\) jest podzielna przez 21, czyli istnieje liczba całkowita k taka, że \(2^{4^n} + 5 = 21k\). Stąd \(2^{4^n} = 21k-5\).
Wobec tego \(2^{4^{n+1}} + 5 = 2^{4^n\cdot 4} + 5 = (2^{4^n})^4 + 5 = (21k - 5)^4 + 5\). Ze wzoru dwumianowego Newtona wynika, że liczbę (21k − 5)4 możemy zapisać jako 21m + 54 dla pewnej liczby całkowitej m (można też przekonać się o tym, wykonując odpowiednie mnożenia). Z tego wynika, że \(2^{4^{n+1}} + 5 = 21m + 5^4 + 5 = 21m + 630 = 21m + 21\cdot 30\),
czyli \(2^{4^n} + 5\)jest liczbą podzielną przez 21.
Zadanie 17.
Udowodnić następującą nierówność Bernoulliego: dla dowolnej liczby rzeczywistej a > − 1 oraz dowolnej liczby naturalnej n zachodzi \((1 + a)^n \geq 1 + na\).
2) Załóżmy, że udowodniliśmy nierówność dla liczb naturalnych od 1 do n, dowodzimy dla n + 1. Korzystając z założenia indukcyjnego otrzymujemy nierówność \((1+a)^{n+1} = (1+a)(1+a)^n \geq (1+a)(1+na)\). Możemy wykonać to przejście, ponieważ a > − 1, czyli 1 + a > 0 - bez tego założenia nie moglibyśmy zastąpić czynnika (1 + a)n przez mniejszą liczbę i mieć pewność, że znak nierówności się nie zmieni.
Przekształcając prawą stronę otrzymanej nierówności, dostajemy \((1+a)(1+na) = 1 + a + na + na^2 = 1 + (n+1)a + na^2 \geq 1 + (n+1)a\). Ostatnia nierówność wynika z tego, że \(na^2 \geq 0\). Tezę otrzymujemy z połączenia otrzymanych nierówności:
\((1+a)^{n+1} \geq (1+a)(1+na) \geq 1+(n+1)a\).
Zadanie 18.
Udowodnić, że dla dowolnej liczby naturalnej \(n \geq 2\) zachodzi nierówność \(2\cdot 4 \cdot 6 \cdots (2n) < (n+1)^n\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 2 do n, dowodzimy dla n + 1. Szacujemy lewą stronę nierówności, korzystając na początku z założenia indukcyjnego:
\(2\cdot 4 \cdot 6 \cdots (2n) \cdot (2n+2) < (n+1)^n\cdot(2n+2) = 2(n+1)^{n+1}\).
Wystarczy więc wykazać, że \(2(n+1)^{n+1} \leq (n+2)^{n+1}\), czyli równoważnie \(2 \leq (\frac{n+2}{n+1})^{n+1} = (1 + \frac{1}{n+1})^{n+1}\).
A tę nierówność można udowodnić, korzystając z nierówności Bernoulliego (biorąc \(a = \frac{1}{n+1}\)): dla dowolnego \(n \in \mathbb{N}\) zachodzi
\((1 + \frac{1}{n+1})^{n+1} \geq 1 + (n+1)\cdot \frac{1}{n+1} = 2\).
Zadanie 19.
Niech \(x_1, x_2, \ldots , x_n\) będą liczbami rzeczywistymi dodatnimi takimi, że \(x_1 \cdot x_2 \cdots x_n = 1\). Wykazać, że wówczas \(x_1 + x_2 + \ldots + x_n \geq n\).
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 2 do n, dowodzimy dla n + 1. Kolejność liczb \(x_1,\ldots , x_{n+1}\) nie jest istotna, więc możemy je przenumerować tak, żeby \(x_{n+1} \geq 1\) oraz \(x_n \leq 1\). (Liczby spełniające te warunki muszą istnieć wśród \(x_1,\ldots , x_{n+1}\), ponieważ nie może być tak, że wszystkie \(x_1,\ldots , x_{n+1}\) są mniejsze od 1 lub wszystkie są większe od 1 - gdyby tak było, ich iloczyn nie byłby równy 1.)
W iloczynie \(x_1\cdot x_2 \cdots x_{n-1} \cdot x_n \cdot x_{n+1}\) traktujemy \(x_n \cdot x_{n+1}\) jako jeden składnik, czyli \(x_1, x_2, \ldots , x_{n-1}, x_n \cdot x_{n+1}\) to n liczb, których iloczyn jest równy 1. Dla tego układu n liczb korzystamy z założenia indukcyjnego, otrzymując nierówność \(x_1 + x_2 + \ldots + x_{n-1} + x_n\cdot x_{n+1} \geq n\).
Jeśli wykażemy, że \(x_n + x_{n+1} -1 \geq x_n \cdot x_{n+1}\), to suma \(x_1 + x_2 + \ldots + x_{n+1} - 1\) będzie większa lub równa lewej stronie powyższej nierówności, czyli również większa lub równa n. A stąd już otrzymamy żądaną nierówność \(x_1 + x_2 + \ldots + x_{n+1} \geq n+1\).
Nierówność \(x_n + x_{n+1} -1 \geq x_n \cdot x_{n+1}\) możemy przekształcić do postaci \(0 \geq x_n \cdot x_{n+1} - x_n - x_{n+1} + 1 = (x_{n+1} -1)(x_n - 1)\).
Teraz musimy przypomnieć sobie, że uporządkowaliśmy liczby \(x_1,\ldots , x_{n+1}\) w taki sposób, że \(x_{n+1} \geq 1\) i \(x_n \leq 1\). Wobec tego \(x_{n+1} -1 \geq 0\) oraz \(x_n - 1\leq 0\), czyli iloczyn tych liczb jest mniejszy lub równy 0.
W ten sposób wykazaliśmy, że \(x_n + x_{n+1} - 1\geq x_n \cdot x_{n+1}\), a stąd, jak zauważyliśmy wcześniej, na mocy zasady indukcji wynika teza zadania.
Zadanie 20.
Udowodnić, że n prostych dzieli płaszczyznę na nie więcej niż 2n części.
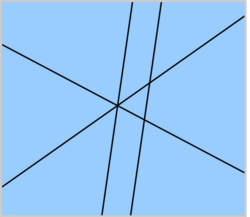
Przykład: 4 proste dzielą płaszczyznę na 9 części. Gdyby trochę rozsunąć trzy proste przecinające się w jednym punkcie, części byłoby więcej.
1) Dla n = 1: jedna prosta dzieli płaszczyznę na dokładnie 2 = 21 części.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 2 do n, dowodzimy dla n + 1. Na płaszczyźnie mamy już n prostych, z założenia indukcyjnego płaszczyzna jest podzielona na co najwyżej 2n części. Dodajemy ostatnią prostą. Zauważmy, że ostatnia prosta może podzielić każdą część na co najwyżej dwie części (czy umiesz uzasadnić to dokładnie?)
Wobec tego po dodaniu ostatniej prostej płaszczyzna może być podzielona na co najwyżej dwa razy więcej części, niż było po narysowaniu n prostych, czyli \(2^n\cdot 2 = 2^{n+1}\).
Zadanie 21.
Udowodnić, że n prostych na płaszczyźnie, z których żadne dwie nie są równoległe i żadne trzy nie przecinają się w jednym punkcie, dzieli płaszczyznę na dokładnie \(\frac{1}{2}(n^2 + n + 2)\) części.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 2 do n, dowodzimy dla n + 1. Na płaszczyźnie mamy już n prostych spełniających warunki zadania. Z założenia indukcyjnego płaszczyzna jest podzielona na dokładnie \(\frac{1}{2}(n^2 + n + 2)\) części. Dodajemy ostatnią prostą. Spróbujmy prześledzić, ile części przecina ta prosta.
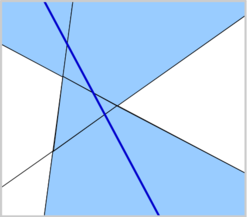
Zauważmy, że prosta przechodzi z jednej części do innej, przecinając którąś z narysowanych wcześniej n prostych. Ponieważ do żadnej nie jest równoległa i przez jeden punkt przecięcia przechodzi tylko jedna z początkowych n prostych, to ostatnia prosta przekracza granicę części dokładnie n razy. To oznacza, że przecina n + 1 części. Każdą z nich dzieli na dwie, więc po dodaniu tej prostej jest o n + 1 więcej części niż wcześniej. Wobec tego w sumie jest ich \(\frac{1}{2}(n^2 + n + 2) + n+1 = \frac{1}{2}(n^2 + n + 2 + 2n + 2) = \frac{1}{2}((n+1)^2 + (n+1) + 2)\), co należało udowodnić.
Zadanie 22.
Udowodnić, że wśród obszarów, na jakie dzieli płaszczyznę n prostych, jest co najwyżej \(\frac{1}{2}(n-1)(n-2)\) ograniczonych.
2) Załóżmy, że udowodniliśmy tezę dla liczb naturalnych od 2 do n, dowodzimy dla n + 1. Na płaszczyźnie mamy już n prostych spełniających warunki zadania. Z założenia indukcyjnego na płaszczyźnie jest co najwyżej \(\frac{1}{2}(n-1)(n-2)\) ograniczonych części. Dodajemy ostatnią prostą. Przecina ona co najwyżej n + 1 części, ponieważ przejście z jednej części do kolejnej wiąże się z przecięciem jednej z n narysowanych prostych. Przynajmniej dwie z tych części, pierwsza i ostatnia, są nieograniczone i ostatnia prosta dzieli je na dwie nieograniczone części (w przeciwnym wypadku te części nie byłyby pierwszą ani ostatnią).
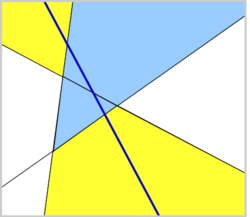
Wobec tego po dodaniu ostatniej prostej przybywa co najwyżej n − 1 ograniczonych części - w sumie jest ich nie więcej niż \(\frac{1}{2}(n-1)(n-2) + n-1 = \frac{1}{2}(n-1)(n-2 + 2) = \frac{1}{2}n(n-1)\).
Zadanie 23.
W każdym polu nieskończonej kartki w kratkę napisano liczbę naturalną tak, że każda z napisanych liczb jest średnią arytmetyczną ośmiu liczb z sąsiednich pól. Wykazać, że liczba 2009 albo nie pojawia się wcale, albo występuje nieskończenie wiele razy.
1) Dla n = 1: załóżmy, że 1 występuje na kartce; wykażemy, że musi wystąpić w każdym polu. Niech \(x_1,\ldots ,x_8\) oznaczają wartości wpisane w pola otaczające 1. Z warunków zadania wynika, że \(\frac{x_1 + \ldots + x_8}{8} = 1\), czyli \(x_1 + \ldots + x_8 = 8\). Ale liczby \(x_1, \ldots , x_8\) są większe lub równe 1, więc żeby spełnić ten warunek, wszystkie muszą być równe 1! Udowodniliśmy, że każde pole, w które wpisana jest 1, jest otoczone polami z wartością 1, a stąd cała kartka jest pokryta jedynkami.
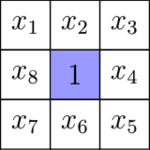
2) Załóżmy, że udowodniliśmy naszą poprawioną tezę dla liczb od 1 do n, dowodzimy dla n + 1. Przyjmijmy, że liczba n + 1 została wpisana w przynajmniej jedno pole. Liczby z sąsiadujących z nim pól oznaczmy przez \(x_1,\ldots ,x_8\). Muszą one spełniać warunek \(x_1+\ldots +x_8 = 8(n+1)\).
Zauważmy, że żadna z liczb \(x_1,\ldots ,x_8\) nie może przyjmować wartości mniejszej niż n + 1. Gdyby przyjmowała, to z założenia indukcyjnego mielibyśmy wniosek, że ta liczba jest wpisana we wszystkie pola, co jest sprzeczne z założeniem, że przynajmniej jedno pole zawiera n + 1. Wobec tego jedyną możliwością spełnienia warunków zadania jest sytuacja, gdy wszystkie liczby \(x_1,\ldots ,x_8\) są równe n + 1. Stąd każde wystąpienie n + 1 jest otoczone wyłącznie przez pola zawierające n + 1, więc n + 1 musi znajdować się w każdym polu.
