Zasada włączeń i wyłączeń

Przypomnijmy z poprzedniego rozdziału wzór wyrażający liczbę elementów sumy dwóch zbiorów w przypadku ogólnym:

\(\qquad|A \cup B| = |A| + |B| - |A \cap B|.\)

Zasada włączeń i wyłączeń dla trzech zbiorów

Podobnym wzorem wyraża się liczba elementów sumy trzech zbiorów:

Wzór ten nosi nazwę zasady włączeń i wyłączeń lub wzoru włączeń i wyłączeń. Nazwa ta bierze się stąd, że liczbę po prawej stronie otrzymujemy,,włączając” do niej trzy liczby | A | , | B | i | C | , potem,,wyłączając” z niej liczby \(|A \cap B|\) , \(|A \cap C|\) i \(|B \cap C|\) i wreszcie,,włączając” do niej liczbę \(|A \cap B \cap C|\) .

Spróbujmy policzyć elementy sumy \(A \cup B \cup C\) . Najpierw liczymy elementy zbioru A , potem elementy zbioru B i wreszcie elementy zbioru C . Otrzymane liczby dodajemy. Mamy więc na razie wynik | A | + | B | + | C | . Teraz zauważamy, że pewne elementy liczyliśmy dwukrotnie: jeśli \(x \in A \cap B\) , to element x był policzony dwukrotnie, raz jako element zbioru A i raz jako element zbioru B . Musimy więc odjąć od wyniku liczbę \(|A \cap B|\) . Podobnie musimy odjąć liczby \(|A \cap C|\) i \(|B \cap C|\) . To jednak jeszcze nie koniec. Zauważamy, że jeśli x jest elementem wszystkich zbiorów, to najpierw był policzony trzykrotnie: raz jako element zbioru A , raz jako element zbioru B i raz jako element zbioru C . Ale potem trzykrotnie policzyliśmy go jako element zbiorów \(A \cap B\) , \(A \cap C\) i \(B \cap C\) . W naszym dotychczasowym wyniku element x trzykrotnie uwzględniliśmy, potem trzykrotnie się go pozbyliśmy. Trzeba więc jeszcze raz go dodać. Stąd wynika, że do wyniku należy dodać liczbę \(|A \cap B \cap C|\) i w ten sposób otrzymujmy prawą stronę wzoru.

Zasada włączeń i wyłączeń: przypadek ogólny

Podobny wzór zachodzi również dla większej liczby zbiorów. Dla czterech zbiorów można jeszcze spróbować go wypisać.

Zasada włączeń i wyłączeń: przypadek czterech zbiorów

Dla większej liczby zbiorów wypisanie odpowiedniego wzoru jest jeszcze bardziej uciążliwe. Widać jednak tę samą, jasną zasadę:

Typowy przykład

Pokażemy dwa przykłady zadań, w których można wykorzystać zasadę włączeń i wyłączeń. Oto pierwszy z nich

Zadanie 1.3.1: W klasie liczącej 33 osoby 17 uczniów uczy się języka włoskiego, 17 uczniów uczy się języka hiszpańskiego i 15 uczniów uczy się języka portugalskiego. Wśród nich 7 uczniów uczy się dwóch języków: włoskiego i hiszpańskiego, 9 uczniów uczy się języka włoskiego i portugalskiego oraz 6 uczniów uczy się języka hiszpańskiego i portugalskiego. Wreszcie 2 uczniów uczy się tych trzech języków. Ilu uczniów nie uczy się żadnego z tych języków?

\(\qquad \begin{array}{c} |W|=17, \, |H|=17, \, |P|=15, \\ |W \cap H|=7, \, |W \cap P|=9, \, |H \cap P|=6, \\ |W \cap H \cap P|=2. \\ \end{array}\)

Z zasady włączeń i wyłączeń wynika, że

\(\qquad |W \cup H \cup P| = 17+17+15-7-9-6+2 = 29.\)

A zatem 4 uczniów nie uczy się żadnego z tych języków.
∎

To zadanie można też rozwiązać, nie odwołując się do zasady włączeń i wyłączeń. Wprowadzimy parę nowych pojęć i oznaczeń, i pokażemy, jak można zasadę włączeń i wyłączeń zastąpić odpowiednio wykonanymi rysunkami.

Zbiór, przestrzeń, dopełnienie, składowe. Jak robić rysunki?

Przypuśćmy, że rozważamy wyłącznie zbiory zawarte w pewnym ustalonym zbiorze X. Zbiór X nazywamy wtedy przestrzenią. Jeśli mamy zbiór A zawarty w przestrzeni X , tzn. \(A \subseteq X\) , to zbiór \(X \setminus A\) nazywamy dopełnieniem (lub uzupełnieniem) zbioru A (czasem dodajemy słowa "do przestrzeni X", dla zaznaczenia, jaką przestrzeń rozważamy) i oznaczamy symbolem A'.

Zauważmy, że różnica zbiorów A i B wyraża się łatwo za pomocą iloczynu i dopełnienia: \(A \setminus B=A \cap B'.\)

Przypuśćmy teraz, że mamy dane dwa zbiory A i B zawarte w przestrzeni X.

Dobrze: dwa zbiory, A i B, w położeniu ogólnym

Często robimy schematyczny rysunek takich zbiorów. Będziemy mówić, że naszkicowane zbiory A i B są w położeniu ogólnym, jeśli na rysunku są uwidocznione cztery obszary odpowiadające zbiorom \(A \cap B\) , \(A \cap B'\) , \(A' \cap B\) i \(A' \cap B'\) .

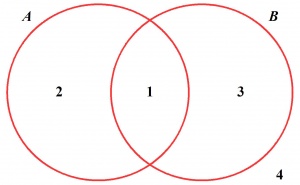
Tak więc na rysunku obok zbiory A i B zostały przedstawione właśnie w położeniu ogólnym. Na tym rysunku zbiory A i B zostały narysowane jako dwa przecinające się okręgi, dzielące płaszczyznę na cztery obszary. Liczby wpisane wewnątrz tych obszarów wskazują, który z czterech zbiorów \(A \cap B\) , \(A \cap B'\) , \(A' \cap B\) i \(A' \cap B'\) odpowiada danemu obszarowi:

\(\begin{array}{ll} 1: & \quad A \cap B, \\ 2: & \quad A \cap B', \\ 3: & \quad A' \cap B, \\ 4: & \quad A' \cap B'. \\ \end{array}\)

Zbiory \(A \cap B\) , \(A \cap B'\) , \(A' \cap B\) i \(A' \cap B'\) nazywamy składowymi zbiorów A i B .

Źle: te pary zbiorów nie są w położeniu ogólnym

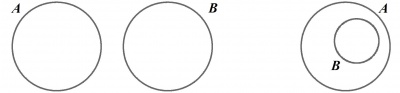
Natomiast na rysunkach obok zbiory A i B nie są przedstawione w położeniu ogólnym.

Dlaczego?

Na lewym z tych rysunków nie jest zaznaczony obszar odpowiadający zbiorowi \(A \cap B\).

Na prawym rysunku nie ma obszaru, który odpowiadałby zbiorowi \(A' \cap B.\)

Podobnie mówimy, że trzy zbiory A , B i C są narysowane w położniu ogólnym, jeśli zaznaczone są obszary odpowiadające ośmiu składowym:

\(\begin{array}{c} A \cap B \cap C, \quad A \cap B \cap C', \quad A \cap B' \cap C, \quad A \cap B' \cap C', \\ A' \cap B \cap C, \quad A' \cap B \cap C', \quad A' \cap B' \cap C, \quad A' \cap B' \cap C'. \\ \end{array}\)

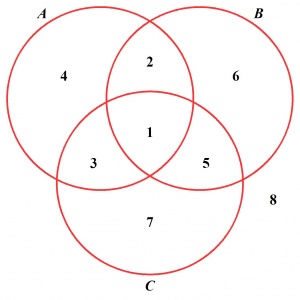
Na poniższym rysunku widzimy trzy zbiory naszkicowane w położeniu ogólnym:

Trzy zbiory, A, B i C, w położeniu ogólnym

Zbiory A, B i C zostały ponownie przedstawione jako trzy przecinające się okręgi, dzielące płaszczyznę na osiem obszarów, które odpowiadają składowym. Liczby wpisane wewnątrz tych ośmiu obszarów wskazują, której składowej odpowiada dany obszar:

\(\begin{array}{ll} 1: & \quad A \cap B \cap C, \\ 2: & \quad A \cap B \cap C', \\ 3: & \quad A \cap B' \cap C, \\ 4: & \quad A \cap B' \cap C', \\ 5: & \quad A' \cap B \cap C, \\ 6: & \quad A' \cap B \cap C', \\ 7: & \quad A' \cap B' \cap C, \\ 8: & \quad A' \cap B' \cap C'. \\ \end{array}\)

Natomiast na rysunku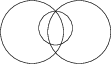

trzy zbiory A , B i C nie są narysowane w położeniu ogólnym, gdyż jedna z ośmiu składowych nie została uwidoczniona.

Zauważmy jeszcze, że składowe są zbiorami parami rozłącznymi (tzn. każde dwie składowe są rozłączne) i w sumie dają całą przestrzeń X .

Kolejne przykłady

Przypomnijmy ostatnie zadanie.

Zadanie 1.3.2: W klasie liczącej 33 osoby 17 uczniów uczy się języka włoskiego, 17 uczniów uczy się języka hiszpańskiego i 15 uczniów uczy się języka portugalskiego. Wśród nich 7 uczniów uczy się dwóch języków: włoskiego i hiszpańskiego, 9 uczniów uczy się języka włoskiego i portugalskiego oraz 6 uczniów uczy się języka hiszpańskiego i portugalskiego. Wreszcie 2 uczniów uczy się tych trzech języków. Ilu uczniów nie uczy się żadnego z tych języków?

Zbiory \(W,\,\, H\) i P. W poszczególne składowe wpisane są liczby ich elementów (można te liczby kolejno wyliczyć, patrz opis obok).

W obszary odpowiadające składowym wpisujemy liczby elementów tych składowych. Zaczynamy od składowej \(W \cap H \cap P\): wpisujmy w odpowiadający jej obszar liczbę 2, gdyż 2 uczniów uczy się wszystkich trzech języków.

Następnie w obszar odpowiadający składowej \(W \cap H \cap P'\) wpisujemy liczbę 5. Dlaczego? Otóż,

\(\qquad (W \cap H \cap P) \cup (W \cap H \cap P') = W \cap H.\)

Wiemy, że zbiór \(W \cap H\) ma 7 elementów, przy czym 2 z nich należą do składowej \(W \cap H \cap P.\) Zatem składowa \(W \cap H \cap P'\) musi mieć 5 elementów.

W podobny sposób stwierdzamy, że

\(\qquad |W' \cap H \cap P|=4 \, \, \mbox{oraz}\, \, |W \cap H' \cap P|=7.\)

Obie liczby wpisujemy w odpowiednie obszary.

Wreszcie, w analogiczny sposób obliczamy, ile elementów mają składowe \(W \cap H' \cap P'\) , \(W' \cap H \cap P'\) oraz \(W' \cap H' \cap P\).

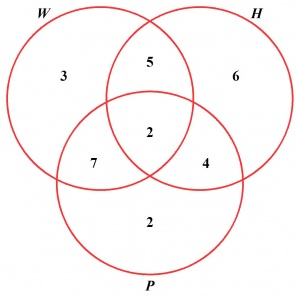
Po wpisaniu wszystkich liczb w odpowiednie obszary dostajemy rysunek, któy został przedstawiony obok. Teraz wystarczy zauważyć, że wszystkie wpisane liczby dają w sumie 29, a więc składowa \(W' \cap H' \cap P'\) ma 33 − 29 = 4 elementy.

∎

Zadanie 1.3.3: W klasie liczącej 31 osób 18 uczniów uczy się języka włoskiego, 16 uczniów uczy się języka hiszpańskiego i 12 uczniów uczy się języka portugalskiego. Wśród nich 7 uczniów uczy się dwóch języków: włoskiego i hiszpańskiego, 9 uczniów uczy się języka włoskiego i portugalskiego oraz 5 uczniów uczy się języka hiszpańskiego i portugalskiego. Wreszcie 3 uczniów nie uczy się żadnego z tych trzech języków. Ilu uczniów uczy się wszystkich języków?

Rozwiązanie:

To zadanie można łatwo rozwiązać za pomocą zasady włączeń i wyłączeń. Mamy bowiem

\(\qquad \begin{array}{ll} |W \cup H \cup P| & = |W| + |H| + |P| - |W \cap H| - |W \cap P| - |H \cap P| + |W \cap H \cap P| = \\ & = 18 + 16 + 12 - 7 - 9 - 5 + |W \cap H \cap P| = 25 + |W \cap H \cap P|. \\ \end{array}\)

Ponieważ 3 uczniów nie uczy się żadnego języka, więc

\(\qquad |W \cup H \cup P| = 31 - 3 = 28.\)

Zatem

\(\qquad 28 = 25 + |W \cap H \cap P|,\)

skąd wynika, że wszystkich trzech języków uczy się 3 uczniów.

∎

Pokażemy teraz rozwiązanie korzystające ze składowych.

Zbiory \(W,\,\, H\) i P. Nie wiemy z początku, ile elementów mają składowe - ale stopniowo układamy równanie.

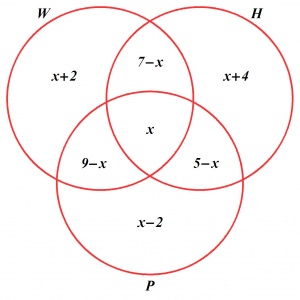
Znów robimy schematyczny rysunek, na którym zaznaczamy zbiory W, H i P w położeniu ogólnym. W polu odpowiadającym składowej \(W \cap H \cap P\) wpisujemy niewiadomą x.

W pola odpowiadające składowym \(W \cap H \cap P'\) , \(W \cap H' \cap P\) oraz \(W' \cap H \cap P\) wpisujemy odpowiednio 7 − x , 9 − x oraz 5 − x. Dlaczego? Chodzi o to, aby każdy z trzech iloczynów \(W \cap H\), \(H \cap P\) i \(W \cap P\) miał odpowiednią liczbę elementów.

Teraz w pola odpowiadające składowym \(W \cap H' \cap P'\) , \(W' \cap H \cap P'\) oraz \(W' \cap H' \cap P\) wpisujemy odpowiednio x + 2, x + 4 i x − 2.

Wiemy też, że zewnętrzna składowa \(W' \cap H' \cap P'\) ma 3 elementy. Dodając wpisane na rysunku liczby do tej trójki, otrzymamy równanie

\(\qquad x+(7-x)+(5-x)+(9-x)+(x+2)+(x+4)+(x-2)+3=31.\)

Jego rozwiązaniem jest liczba 3, a więc trzech uczniów uczy się wszystkich języków.