Żeby lepiej zrozumieć własności stycznych do okręgu, przyjrzyjmy się kilku przykładom. Niektóre rozwiązania przykładowych zadań będziemy przedstawiać jako ciągi kolejnych spostrzeżeń, które można traktować jako wskazówki, tak aby w dowolnym momencie można było przerwać czytanie i dokończyć rozwiązanie samodzielnie.
Na początku zdefiniowaliśmy styczną jako prostą, która ma z okręgiem dokładnie jeden punkt wspólny. Jest to jednak mało praktyczna definicja, trudno ją wykorzystać w zadaniach. Zwykle dużo łatwiej jest użyć własności zawartej w Twierdzeniu 1: styczna jest prostopadła do promienia poprowadzonego do punktu styczności. Ta własność charakteryzuje styczne do okręgów, co oznacza, że twierdzenie działa również w drugą stronę: jeśli prosta k przecina okrąg o środku O w punkcie A i wykażemy, że jest ona prostopadła do promienia OA, to k jest styczną do danego okręgu. A zwykle dużo łatwiej jest wykonać obliczenia miar kątów, niż wykazać, że dwie figury mają tylko jeden punkt wspólny.
Pomyślmy, co możemy wywnioskować z pojawienia się na rysunku prostej stycznej do pewnego okręgu (lub jej odcinka). Na pewno można zacząć od narysowania promienia do punktu styczności i zaznaczenia kąta prostego. Być może w tym momencie na rysunku widać już jakieś trójkąty prostokątne. Dlaczego chcielibyśmy je widzieć? O trójkątach prostokątnych można powiedzieć całkiem dużo: czasami łatwo wyznaczyć miary ich kątów, bo jeden kąt jest już znany, do dyspozycji jest twierdzenie Pitagorasa, podstawowe funkcje trygonometryczne, a ponadto okręgi wpisane i opisane na tych trójkątach mają różne ciekawe własności... Szczególnie ciekawe pod tym względem jest zadanie 5.
A jeśli zaznaczenie kąta prostego pomiędzy styczną i promieniem nie powoduje powstania trójkąta prostokątnego na rysunku? Wtedy pewnie trzeba jakąś kreskę dorysować, żeby mieć odpowiedni trójkąt, w którym kąt prosty pozwoli uzyskać nowe informacje.
Przykład 1 (Zadanie 2)
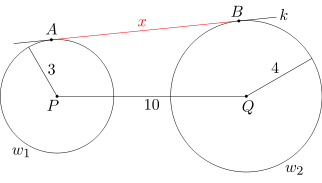
Dany jest odcinek PQ o długości 10 oraz okręgi: jeden o środku P i promieniu 3, a drugi o środku Q i promieniu 4. Okręgi te leżą po jednej stronie prostej k, która jest do nich styczna odpowiednio w punktach A i B. Oblicz długość odcinka AB.
Uwaga: Jeśli prosta k jest styczna do dwóch okręgów i oba te okręgi leżą po tej samej stronie prostej k, to mówimy, że prosta k jest wspólną styczną zewnętrzną tych okręgów.
Rozwiązanie
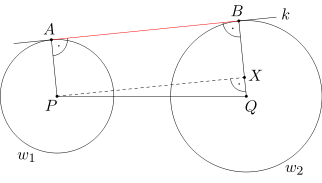
Zaczniemy od wykorzystania otrzymanych w treści zadania informacji o styczności prostej k do danych okręgów - dorysujmy promienie PA i QB oraz zaznaczmy kąty proste pomiędzy nimi a prostą k. Ponieważ odcinki PA i QB są prostopadłe do prostej k, to są równoległe. Wobec tego czworokąt PQBA, który powstał na rysunku po dorysowaniu promieni, jest trapezem - co więcej, trapezem prostokątnym, a bok AB jest jego wysokością, jako że jest prostopadły do podstaw.
Co możemy zrobić, jeśli na rysunku pojawiają się kąty proste, a naszym celem jest obliczenie długości pewnego odcinka? Intuicja podpowiada, że w tej sytuacji do wykonania obliczeń ma szanse przydać się twierdzenie Pitagorasa. Tylko na razie na rysunku nie mamy ani jednego trójkąta prostokątnego - spróbujmy więc go znaleźć!
Można na przykład zrobić trójkąt prostokątny z trapezu PQBA. W jaki sposób? Wystarczy rozciąć go wysokością poprowadzoną z punktu P na prostokąt ABPX i trójkąt prostokątny XPQ, jak na rysunku poniżej.
Zajmijmy się trójkątem XPQ. Utworzenie go wygląda na dobry krok, ponieważ jednym z jego boków jest odcinek XP, który ma tę samą długość, co szukany odcinek AB (czy umiesz wyjaśnić dlaczego?). Sprawdźmy, czy wiemy o tym trójkącie na tyle dużo, żeby umieć znaleźć długość boku XP. Ze sformułowania zadania znamy długość przeciwprostokątnej PQ. Zauważmy, że odcinek QX i odcinek XB sumują się do promienia QB o długości 4. A długość odcinka XB jest taka sama, jak długość promienia PA (czy to również umiesz uzasadnić?), czyli wynosi 3. Wobec tego odcinek QX ma długość 4 - 3 = 1.
Teraz możemy zastosować twierdzenie Pitagorasa do trójkąta XPQ:
XP2 + QX2 = PQ2,
więc XP2 = 102 − 12,
a stąd \(XP = \sqrt{99} = 3\sqrt{11}\).
A ponieważ odcinki XP i AB mają tę samą długość, to ostatecznie \(AB = 3\sqrt{11}\).
Ponieważ rozwiązując powyższe zadanie, a także zadanie 3, musimy narysować wspólne styczne do dwóch okręgów, a ponadto wykonane rysunki zbliżają nas do konstrukcji tych stycznych, naszkicujemy sposób ich konstruowania.
Następny przykład jest trochę trudniejszy, ale rozwiązanie opiera się na tej samej metodzie: wykorzystaniu prostopadłości stycznej do promienia i własności trójkątów prostokątnych. Po przeczytaniu kolejnych kroków rozwiązania warto sprawdzać, czy rozwiązanie nie leży już w zasięgu ręki.
Przykład 2 (Zadanie 5)
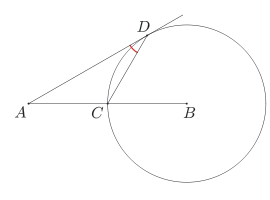
Punkt C jest środkiem odcinka AB. Niech w będzie okręgiem o środku B przechodzącym przez punkt C. Przez punkt A poprowadzono prostą, która jest styczna do okręgu w w punkcie D. Oblicz miarę kąta ADC.
Rozwiązanie
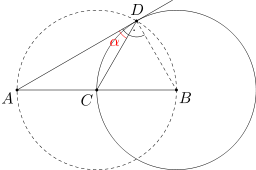
Znamy już miarę kąta ADB - wobec tego warto mieć ten kąt na rysunku. Trzeba dorysować brakujące ramię, czyli promień BD. Dzięki temu mamy na rysunku trójkąt prostokątny ABD - spróbujmy powiedzieć o nim coś więcej.
Czy widać, jaką funkcję pełni punkt C w tym trójkącie?
Punkt C jest środkiem przeciwprostokątnej. Wiadomo, że środek okręgu opisanego na trójkącie prostokątnym leży właśnie na środku przeciwprostokątnej. Wobec tego punkty A, B i D leżą na okręgu, którego środkiem jest punkt C. Jakie informacje dotyczące długości odcinków na rysunku możemy stąd otrzymać?
Odcinki CA, CB i CD to promienie okręgu opisanego na trójkącie ADB, więc są równe. Czyli na rysunku znajdują się dwa trójkąty równoramienne: ACD i BCD. O jednym z nich można powiedzieć jeszcze więcej...
Przyjrzyjmy się dokładniej trójkątowi BCD. Zauważyliśmy już, że CB=CD. Ponadto odcinki BC i BD mają tę samą długość, ponieważ są promieniami okręgu w. A to oznacza, że trójkąt BCD jest równoboczny.
Pozostaje łatwy rachunek: miara kąta BCD wynosi \(60^\circ\), czyli miara kąta ADC jest równa \(90^\circ - \angle BCD = 30^\circ\).
Twierdzenie 2 mówi, że jeśli z punktu A poza danym okręgiem poprowadzimy dwie styczne, to odcinki od punktu A do punktów styczności będą miały tę samą długość. To spostrzeżenie wydaje się oczywiste (i właściwie takie jest) - przecież okrąg jest figurą bardzo symetryczną, taką samą z każdej strony, więc właściwie jak moglibyśmy dostać w ten sposób różne odcinki? Jednak tak często przydaje się w zadaniach, że nie można o nim zapominać i warto przyjrzeć się dokładniej zastosowaniom.
Przykład 3 (Zadanie 7)
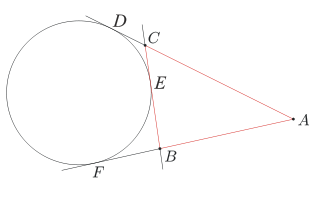
Dany jest trójkąt ABC. Okrąg w jest styczny do odcinka BC oraz do przedłużeń boków AC i AB. Niech F będzie punktem styczności okręgu w z prostą AB. Udowodnij, że połowa obwodu trójkąta ABC jest równa długości odcinka AF.
Uwaga
Na początek podchwytliwe pytanie: czy nie wydaje się dziwne, że w treści zadania występuje odcinek AF, i jego długość ma się ładnie wyrażać przez długości boków trójkąta ABC, a nie występuje punkt styczności danego okręgu z przedłużeniem boku AC (oznaczmy go D)? Dlaczego ten punkt miałby mieć inne własności niż punkt F?
Okazuje się, że w treści zadania może się pojawić dowolny z tych punktów. Po prostu odcinki AF i AD mają tę samą długość, ponieważ są odcinkami łączącymi punkt A z punktami przecięcia z okręgiem w stycznych poprowadzonych do niego z A.
Rozwiązanie
Oznaczmy przez D punkt styczności okręgu w z przedłużeniem boku AC, a przez E punkt styczności z bokiem BC. Zabierzmy się za rozwiązywanie zadania przy pomocy Twierdzenia 2 - na przykład spróbujmy wypisać wszystkie punkty, z których prowadzimy dwie styczne do okręgu, i wynikające z tych sytuacji równości odcinków.
Po pierwsze, styczne z punktu A dają równość AF = AD (a).
Po drugie, styczne z punktu B dają równość BF = BE (b).
W końcu z punktu C też wyprowadzamy dwie styczne i otrzymujemy równość CD = CE (c).
Spróbujmy zobaczyć, jak te równości pozwolą nam opisać długość odcinka AF. Przede wszystkim odcinek AF jest podzielony punktem B, więc możemy zapisać AF = AB + BF = AB + BH, korzystając z równości (b). Wydaje się, że lepiej mieć w opisie odcinek BE, niż BF, ponieważ BE jest częścią obwodu trójkąta. Podobnie, korzystając z równości (c), możemy zapisać, że AD = AC + CD = AC + CE.
Popatrzmy na rysunek: widzimy, że odcinki, które sumują się do długości odcinków AF i AD, czyli AB, AC, BE i CE, dają w sumie cały obwód trójkąta! Zaczynając z punktu A i idąc po obwodzie w prawo, skręcając w punkcie C i zatrzymując się w E, pokonujemy trasę równą odcinkowi AD. Natomiast idąc w lewo i skręcając w punkcie B do punktu E, przechodzimy długość odcinka AF. I mamy jeszcze niewykorzystaną równość (a) - mówi ona dokładnie tyle, że te dwie drogi są równe. A jeśli są równe i sumują się do obwodu trójkąta, ta każda z nich jest połową obwodu. Czyli długość odcinka AF (oraz AD) to połowa obwodu trójkąta, co należało wykazać.
Używając metod opisanych w poprzednim przykładzie, warto spróbować rozwiązać kolejne zadanie, korzystając z kolejnych wskazówek, jeśli są potrzebne.
Przykład 4 (Zadanie 10)
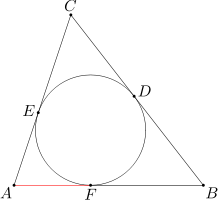
Okrąg wpisany w trójkąt ABC jest styczny do boków BC, CA, AB odpowiednio w punktach D, E, F. Wiedząc, że długości boków BC, CA, AB wynoszą odpowiednio a, b, c, oblicz długość odcinka AF.
Rozwiązanie
Jeśli okrąg jest wpisany w trójkąt (lub dopisany do trójkąta, jak w poprzednim przykładzie), to takimi punktami są jego wierzchołki.
Jeśli okrąg jest wpisany w trójkąt (lub dopisany do trójkąta, jak w poprzednim przykładzie), to takimi punktami są jego wierzchołki.
Z Twierdzenia 2 otrzymujemy równości odcinków: AD = AF, BF = BE, CE = CD.
Wiemy, że AF = AD. Wobec tego, gdybyśmy umieli wyznaczyć sumę tych odcinków, to dzieląc ją przez 2 otrzymalibyśmy szukaną długość odcinka AF. Spróbujmy więc wyznaczyć sumę długości tych odcinków.
Żeby obliczyć sumę długości odcinków AD i AF, można obliczyć długość pozostałej części obwodu trójkąta i odjąć ją od długości całego obwodu, czyli a+b+c. Długość odcinka BC jest dana - co z pozostałymi odcinkami, CD i BF?
Ponieważ CD = CE oraz BE = BF, to długości odcinków CD i BF sumują się do długości boku BC, czyli b.
Teraz wystarczy wykonać obliczenia. Suma długości odcinków AF i AD wynosi (AB + AC + BC) - (CD + BF + CB) = a+b+c - 2b = a+c-b. A stąd odcinek AF ma długość (a+c-b)/2.
Twierdzenie o stycznej i cięciwie (Twierdzenie 3) można bardzo łatwo i szybko udowodnić, wykonując rachunek na kątach. Ale umieszczanie tych dwóch linijek dowodu w opisach wielu rozwiązanych zadań byłoby bardzo uciążliwe, więc dużo lepiej jest zapamiętać tę własność. Zobaczmy, jak użycie tego twierdzenia skraca pracę i upraszcza rozwiązania.
Zaczniemy od prostego zadania, którego rysunek jest bardzo podobny, jak w poprzednim przykładzie - ale rozwiązanie będzie używać zupełnie innych własności stycznych.
Przykład 5 (Zadanie 11)
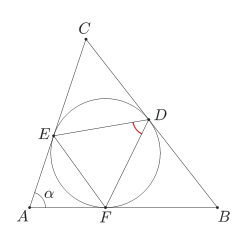
Okrąg wpisany w trójkąt ABC jest styczny do boków BC, CA, AB odpowiednio w punktach D, E, F. Wiedząc, że miara kąta BAC wynosi α, oblicz miarę kąta EDF.
Rozwiązanie
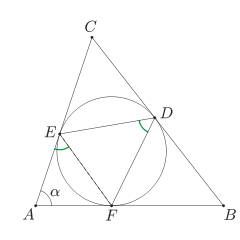
Popatrzmy na rysunek i zastanówmy się, jakich metod możemy użyć, żeby wyznaczyć miarę kąta EDF. Czy umiemy jakoś porównać miarę tego kąta z miarami innych kątów na rysunku? O których kątach na rysunku w ogóle coś wiemy?
Można na przykład próbować obliczyć miary kątów FED i EFD, a następnie wyznaczyć miarę trzeciego kąta w trójkącie DEF. Ale właściwie nie widać, dlaczego obliczenie miar tych kątów miałoby być łatwiejsze, niż obliczenie miary kąta EDF bezpośrednio. Można też obliczyć miary kątów CDE i BDF, a potem wyznaczyć miarę kąta EDF jako dopełniającego tamte dwa do kąta półpełnego. Ale znów o kątach CDE i BDF, a nawet o którychkolwiek kątach w trójkątach CDE i BDF, nic nie wiemy.
Mamy natomiast dane o kątach trójkąta AEF. Właściwie tylko o jednym kącie - miara kąta EAF, czyli kąta BAC, jest równa α. A co z pozostałymi? Tu warto spojrzeć na poprzedni przykład i Twierdzenie 2: punkty E i F są punktami wspólnymi danego okręgu i stycznych poprowadzonych z punktu A, więc odcinki AE i AF są równe. Czyli trójkąt AEF jest równoramienny i miary kątów AEF i AFE wynoszą \((180^\circ - \alpha)/2\).
Ale jak powiązać te kąty z szukanym kątem EDF? Tu właśnie przyda się twierdzenie o stycznej i cięciwie. Kąt EDF jest wpisany w dany okrąg, oparty na łuku EF. Wobec tego z Twierdzenia 3 jego miara jest taka sama, jak miara kąta pomiędzy cięciwą EF a styczną do okręgu w punkcie E (lub styczną w punkcie F - jak wiemy, te kąty są takie same). A kąt pomiędzy cięciwą EF a styczną w punkcie E to kąt AEF, którego miarę obliczyliśmy przed chwilą. Wobec tego miara kąta DEF wynosi \({(180^\circ - \alpha)\over2} = 90^\circ-{\alpha\over2}\).
Czasami może być łatwiej wymyślić rozwiązanie nie używające twierdzenia o stycznej i cięciwie, chociażby dlatego, że można zapomnieć o istnieniu takiego twierdzenia. Ale takie rozwiązanie okazuje się zwykle dłuższe w opisie. Obejrzyjmy różnicę na poniższym przykładzie, który ponadto pokazuje, jak korzystać z drugiej połowy twierdzenia o kącie między styczną a cięciwą.
Przykład 6 (Zadanie 15)
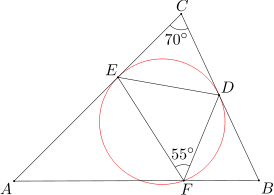
Dany jest trójkąt ABC, w którym miara kąta przy wierzchołku C równa się 70 stopni. Punkty D, E, F leżą odpowiednio na bokach BC, CA, AB, przy czym CE=CD oraz miara kąta DFE wynosi 55 stopni. Wykaż, że okrąg opisany na trójkącie DEF jest styczny do prostych BC i CA.
Rozwiązanie bez Twierdzenia 3 (być może łatwiejsze do wymyślenia)
Oznaczmy środek okręgu opisanego na trójkącie DEF przez O. Musimy wykazać, że promienie OD i OE są prostopadłe do prostych BC i AC - wtedy będziemy wiedzieli, że okrąg jest styczny do boków BC i CA.
W tym celu obliczymy miary kilku kątów. Kąt środkowy DOE ma dwukrotnie większą miarę, niż kąt wpisany DFE; wobec tego jego miara wynosi 110 stopni. Zauważmy, że trójkąt DOE jest równoramienny, ponieważ boki OD i OE są promieniami okręgu. Wobec tego miary kątów OED i ODE są równe i wynoszą \((180^\circ - 110^\circ)/2 = 35^\circ\).
Natomiast z warunków zadania wynika, że trójkąt CED jest równoramienny (CE = CD), więc miary kątów DEC i EDC są równe i wynoszą \((180^\circ - 70^\circ)/2 = 55^\circ\). Teraz możemy obliczyć miary kątów ODC i OEC:
\(\angle OEC = \angle OED + \angle DEC = 35^\circ + 55^\circ = 90^\circ\)
i tak samo \(\angle ODC = \angle ODE + \angle EDC = 35^\circ + 55^\circ = 90^\circ\),
czyli (z Twierdzenia 1) punkty D i E są punktami styczności okręgu opisanego na trójkącie DEF z bokami AC i BC.
Rozwiązanie używające Twierdzenia 3 (krótsze i bardziej eleganckie)
Ponieważ odcinki CD i CE są równe, to trójkąt CDE jest równoramienny - miary kątów CDE i CED wynoszą \((180^\circ - 70^\circ)/2 = 55^\circ\).
Popatrzmy na kąty EFD i CED. Mają tę samą miarę, 55 stopni. Ponadto kąt EFD jest wpisany w dany okrąg, oparty na łuku ED. Natomiast kąt CED to kąt pomiędzy cięciwą ED i pewną prostą przechodzącą przez punkt E. Naszym celem jest wykazanie, że ta prosta jest styczna do danego okręgu.
O takiej sytuacji mówi druga połowa Twierdzenia 3, będąca twierdzeniem odwrotnym do pierwszej, częściej używanej: jeśli kąt wpisany oparty na cięciwie ED i kąt między cięciwą ED a pewną prostą przechodzącą przez punkt E mają taką samą miarę, to ta prosta jest styczna do okręgu (oczywiście w punkcie E). Wykazaliśmy więc, że prosta AC jest styczna do okręgu opisanego na trójkącie DEF. Tak samo przebiega uzasadnienie, że prosta BC jest styczna do tego okręgu - warto je zapisać dla ćwiczenia.
Rozwiązanie ostatniego przykładowego zadania jest podzielone na ciąg wskazówek.
Przykład 7 (Zadanie 17)
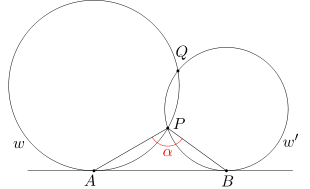
Okręgi w oraz w' przecinają się w punktach P i Q. Do okręgów w oraz w' poprowadzono wspólną styczną zewnętrzną AB (przyjmujemy, że styczna ta leży bliżej punktu P niż punktu Q). Wiedząc, że długość łuku AP stanowi 1/6 długości łuku okręgu w, a długość łuku PB stanowi 1/5 długości okręgu w', oblicz miarę kąta APB.
Rozwiązanie
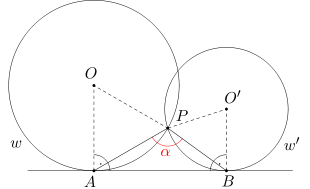
Zacznijmy od ważnej uwagi ogólnej: jak wykorzystać informację o długości pewnego łuku, a dokładniej o tym, jakim ułamkiem całego okręgu jest ten łuk. Najłatwiej będzie spojrzeć na kąty środkowe:
kąt środkowy jest takim ułamkiem kąta pełnego, jakim ułamkiem długości okręgu jest długość łuku, na którym jest oparty.
Na przykład, jeśli długość łuku AP to 1/6 długości całego okręgu, to miara kąta środkowego opartego na łuku AP jest równa \(360^\circ/6 = 60^\circ\). A jeśli długość łuku PB stanowi 1/5 długości okręgu, to miara kąta środkowego opartego na łuku PB jest równa \(360^\circ/5 = 72^\circ\). Te obliczenia pewnie przydadzą się dalej w rozwiązaniu.
Przez O i O' oznaczmy odpowiednio środki okręgów w i w'. Zauważmy, że miarę kąta BAP prawie możemy obliczyć korzystając z twierdzenia o kącie między styczną i cięciwą - prawie, ponieważ na razie znamy tylko miarę kąta środkowego AOP opartego na cięciwie AP, a nie kąta wpisanego...
Ale to żaden problem! Wiemy, że (każdy) kąt wpisany oparty na łuku AP ma miarę dwukrotnie mniejszą niż kąt środkowy oparty na tym samym łuku. Wobec tego miara kąta wpisanego opartego na łuku AP to 60/2 = 30 stopni. Z twierdzenia o kącie między styczną a cięciwą kąt BAP również ma miarę 30 stopni.
W ten sam sposób wyznaczamy miarę kąta ABP - wynosi ona 36 stopni.
Stąd ostatecznie miara kąta APB równa się 180-36-30=114 stopni.
