Zaprezentowane rozwiązania są tylko przykładami prawidłowych rozwiązań - większość z zadań można bowiem rozwiązać na wiele sposobów. Zachęcamy Czytelników do podjęcia samodzielnej próby znalezienia własnych metod rozwiązania.
Zadanie 1
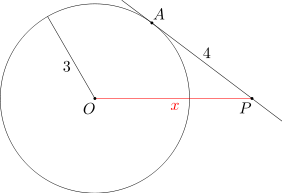
Dany jest okrąg o środku O i promieniu 3. Przez punkt P leżący na zewnątrz tego okręgu poprowadzono prostą, która jest styczna do danego okręgu w punkcie A. Wiedząc, że długość odcinka AP wynosi 4, oblicz długość odcinka OP.
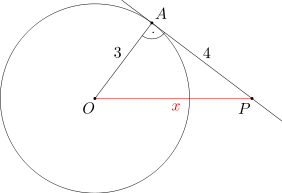
Ponieważ punkt A jest punktem styczności danego okręgu oraz prostej AP, więc kąt OAP jest prosty. Wobec tego wykorzystując twierdzenie Pitagorasa uzyskujemy kolejno:
OP2 = OA2 + AP2,
OP2 = 32 + 42,
OP = 5.
Zadanie 2
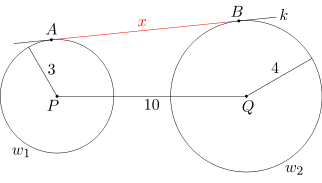
Dany jest odcinek PQ o długości 10 oraz okręgi: jeden o środku P i promieniu 3, a drugi o środku Q i promieniu 4. Okręgi te leżą po jednej stronie prostej k, która jest do nich styczna odpowiednio w punktach A i B. Oblicz długość odcinka AB.
Uwaga: Jeśli prosta k jest styczna do dwóch okręgów i oba te okręgi leżą po tej samej stronie prostej k, to mówimy, że prosta k jest wspólną styczną zewnętrzną tych okręgów.
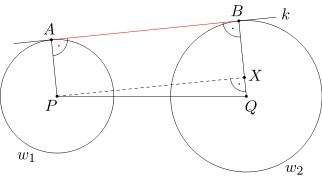
Niech X będzie takim punktem leżącym na odcinku BQ, że długość odcinka BX wynosi 3. Ponieważ kąty XBA oraz BAP są proste, więc odcinki AP i BX są równoległe. Ponadto odcinki te są równej długości, skąd wynika, że czworokąt ABXP jest równoległobokiem. A ponieważ w równoległoboku tym kąt ABX jest prosty, więc równoległobok ten jest prostokątem.
Wobec tego trójkąt PXQ jest trójkątem prostokątnym. Korzystając z twierdzenia Pitagorasa uzyskujemy kolejno:
PQ2 = PX2 + XQ2,
PQ2 = AB2 + (BQ − BX)2,
102 = AB2 + (4 − 3)2.
Stąd otrzymujemy ostatecznie:
\(AB=3\sqrt{11}.\)
Zadanie 3
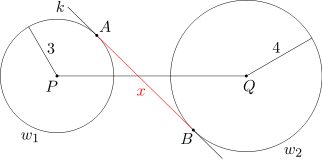
Dany jest odcinek PQ o długości 10 oraz okręgi: jeden o środku P i promieniu 3, a drugi o środku Q i promieniu 4. Okręgi te leżą po przeciwnych stronach prostej k, która jest do nich styczna odpowiednio w punktach A i B. Oblicz długość odcinka AB.
Uwaga: Jeśli prosta k jest styczna do dwóch okręgów i oba te okręgi leżą po przeciwnych stronach prostej k, to mówimy, że prosta k jest wspólną styczną wewnętrzną tych okręgów.
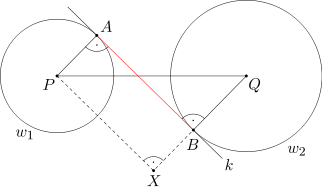
Niech X będzie takim punktem leżącym na prostej BQ, poza odcinkiem BQ, że długość odcinka BX wynosi 3. Ponieważ proste AP i BX są prostopadłe do wspólnej prostej AB, więc odcinki AP i BX są równoległe. Ponadto odcinki te są równej długości, skąd wynika, że czworokąt APXB jest równoległobokiem. A ponieważ w równoległoboku tym kąt PAB jest prosty, więc równoległobok ABXP jest prostokątem.
Zatem trójkąt PXQ jest trójkątem prostokątnym. Korzystając z twierdzenia Pitagorasa uzyskujemy:
PQ2 = PX2 + XQ2,
PQ2 = AB2 + (BQ + BX)2,
102 = AB2 + (4 + 3)2.
Stąd otrzymujemy ostatecznie:
\(AB=\sqrt{51}.\)
Zadanie 4
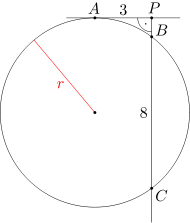
Punkt P leży na zewnątrz okręgu w. Przez punkt P poprowadzono prostą, która jest styczna do okręgu w w punkcie A. Przez punkt P poprowadzono także prostą prostopadłą do prostej AP, która przecina okrąg w w punktach B i C. Wiedząc, że długość odcinka AP wynosi 3, a długość odcinka BC równa się 8, oblicz długość promienia okręgu w.
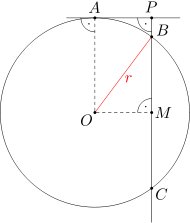
Niech O będzie środkiem danego okręgu, a M środkiem odcinka BC. Ponieważ trójkąt OBC jest trójkątem równoramiennym (odcinki OB i OC są równe promieniowi danego okręgu), więc odcinek OM jest wysokością w tym trójkącie. Stąd wnioskujemy, że trójkąt OMB jest trójkątem prostokątnym.
Zauważmy, że w czworokącie APMO trzy kąty są proste: kąt OAP jest prosty, gdyż prosta PA jest styczna do okręgu w w punkcie A, kąt APM jest prosty, gdyż prosta PM jest prostopadła do prostej AP oraz kąt OMB jest prosty, co uzasadniliśmy na początku rozwiązania. Stąd wynika, że czworokąt APMO jest prostokątem. W szczególności, długości odcinków AP i OM są równe.
Oznaczając przez r promień danego okręgu oraz wykorzystując twierdzenie Pitagorasa dla trójkąta OMB otrzymujemy kolejno:
OB2 = OM2 + MB2,
OB2 = AP2 + MB2,
r2 = 32 + 42,
r = 5.
Zadanie 5
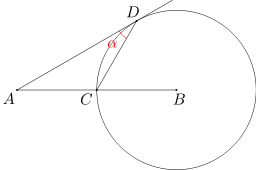
Punkt C jest środkiem odcinka AB. Niech w będzie okręgiem o środku B przechodzącym przez punkt C. Przez punkt A poprowadzono prostą, która jest styczna do okręgu w w punkcie D. Oblicz miarę kąta ADC.
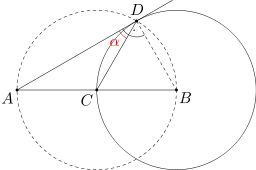
Ponieważ prosta AD jest styczna do okręgu w w punkcie D, więc kąt ABD jest prosty. Wobec tego środek okręgu opisanego na trójkącie prostokątnym ABD pokrywa się ze środkiem przeciwprostokątnej AB, czyli z punktem C.
A zatem odcinki BC i CD są równej długości (są to promienie okręgu opisanego na trójkącie ABD), a ponadto odcinki BC i BD są równej długości (gdyż są to promienie danego okręgu w). Stąd wynika, że trójkąt BCD jest trójkątem równobocznym, a więc miara kąta BDC równa się 60 stopni. Wobec tego miara kąta ADC wynosi 90-60=30 stopni.
Zadanie 6
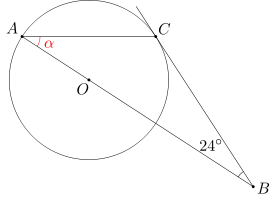
Dany jest okrąg o środku O oraz punkty A, C leżące na nim. Styczna do tego okręgu w punkcie C przecina prostą AO w punkcie B. Wiedząc, że miara kąta ABC wynosi 24 stopnie, oblicz miarę kąta CAB.
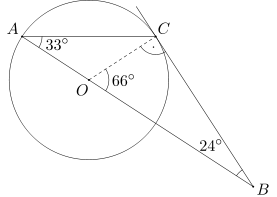
Ponieważ prosta BC jest styczna do danego okręgu w punkcie C, więc kąt BCO jest prosty. Stąd wynika, że miara kąta COB wynosi 90-24=66 stopni.
Zauważmy, że trójkąt ACO jest trójkątem równoramiennym (odcinki OA i OC są równej długości, gdyż są one promieniami danego okręgu). Stąd wynika, że miara kąta BAC jest równa 66:2=33 stopnie.
Zadanie 7
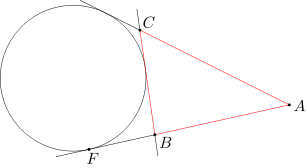
Dany jest trójkąt ABC. Okrąg w jest styczny do odcinka BC oraz do przedłużeń boków AC i AB. Niech F będzie punktem styczności okręgu w z prostą AB. Udowodnij, że połowa obwodu trójkąta ABC jest równa długości odcinka AF.
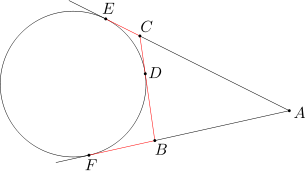
Niech D, E będą punktami styczności okręgu w odpowiednio z prostymi BC i AC. Wówczas CD=CE, BD=BF oraz AE=AF. Stąd otrzmujemy
AB+BC+CA=AB+BD+DC+CA=AB+BF+CE+CA=AF+AE=2AE.
Dzieląc uzyskaną równość stronami przez 2 uzyskujemy tezę.
Zadanie 8
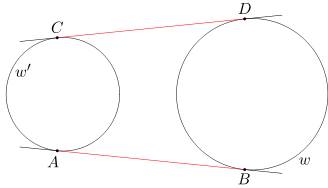
Dane są okręgi w oraz w'. Do obu tych okręgów poprowadzono dwie wspólne styczne zewnętrzne AB i CD. Udowodnij, że długości odcinków AB i CD są równe.
1. Okręgi w oraz w' mają równe promienie. Wykaż, że wówczas każdy z odcinków AB i CD ma długość równą długości odcinka PQ, gdzie P i Q są odpowiednio środkami okręgów w oraz w'.
2. Okręgi w oraz w' mają różne promienie. Wówczas proste AB i CD przecinają się.
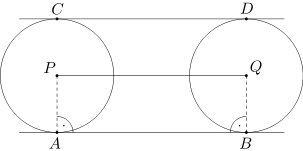
1. Okręgi w oraz w' mają równe promienie. Oznaczmy przez Q, P środki odpowiednio okręgów w, w'. Ponieważ prosta AB jest styczna do okręgów w oraz w' odpowiednio w punktach B oraz A, więc kąty PAB i ABQ są proste. Wynika stąd, że odcinki AP i BA są równoległe. Ponadto odcinki te są równej długości, więc czworokąt ABQP jest równoległobokiem. Stąd otrzymujemy równość AB=PQ.
Analogicznie dowodzimy, że CD=PQ. Ostatecznie zatem AB=CD.
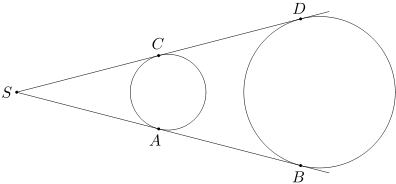
2. Okręgi w oraz w' mają różne promienie. Wówczas proste AB i CD przecinają się w pewnym punkcie S. Wobec tego AS=CS oraz BS=DS. Z równości tych wynika bezpośrednio, że AB=CD.
Zadanie 9
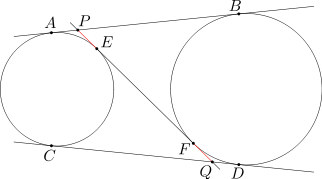
Dane są rozłączne okręgi w oraz w'. Do obu tych okręgów poprowadzono wspólne styczne zewnętrzne AB i CD. Wspólna styczna wewnętrzna EF tych okręgów przecina proste AB i CD odpowiednio w punktach P i Q. Wykaż, że długości odcinków EP i FQ są równe.
Korzystając z równości AB=CD (poprzednie zadanie) uzyskujemy zależność 2x+y=2z+y, skąd bezpośrednio otrzymujemy x=z, czyli EP=FQ.
Zadanie 10
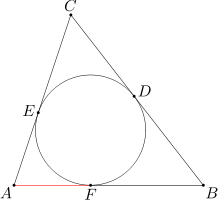
Okrąg wpisany w trójkąt ABC jest styczny do boków BC, CA, AB odpowiednio w punktach D, E, F. Wiedząc, że długości boków BC, CA, AB wynoszą odpowiednio a, b, c, oblicz długość odcinka AF.
W tym celu mnożymy drugie równanie stronami przez -1, po czym dodajemy stronami wszystkie trzy równania. W efekcie otrzymujemy x+y-y-z+z+x=b+c-a, czyli 2x=b+c-a. Stąd ostatecznie x=(b+c-a)/2.
Zadanie 11
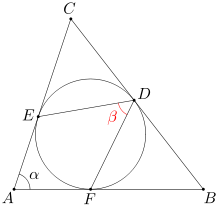
Okrąg wpisany w trójkąt ABC jest styczny do boków BC, CA, AB odpowiednio w punktach D, E, F. Wiedząc, że miara kąta BAC wynosi α, oblicz miarę kąta EDF.
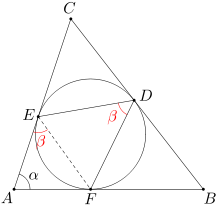
Ponieważ AE=AF, więc trójkąt AEF jest równoramienny. Stąd wynika, że
\(\angle AEF=90^\circ-{\alpha\over2}.\)
Korzystając z twierdzenia o kącie między styczną a cięciwą wnioskujemy, że
\(\angle EDF=\angle AEF=90^\circ-{\alpha\over2}.\)
Zadanie 12
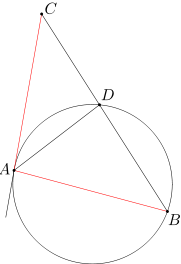
Dany jest trójkąt ABC. Okrąg przechodzący przez punkty A i B styczny do prostej AC w punkcie A, przecina bok BC w punkcie D. Udowodnij, że jeśli AD=CD, to trójkąt ABC jest równoramienny.
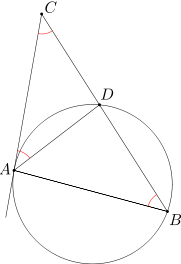
Ponieważ AD=CD, więc trójkąt ADC jest trójkątem równoramiennym, a zatem miary kątów CAD i ACB są równe. Ponadto z twierdzenia o kącie między styczną a cięciwą wynika, że miary kątów CAD i ABC są równe. Wobec tego miary kątów ACB i ABC są równe, czyli trójkąt ABC jest trójkątem równoramiennym.
Zadanie 13
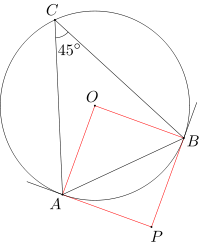
Dany jest trójkąt ABC, w którym miara kąta ACB wynosi 45 stopni. Punkt O jest środkiem okręgu w opisanego na tym trójkącie. Styczne do okręgu w w punktach A i B przecinają się w punkcie P. Wykaż, że czworokąt APBO jest kwadratem.
Wykazaliśmy zatem, że w czworokącie AOBP trzy kąty wewnętrzne są proste, a więc czworokąt ten jest prostokątem. Aby wywnioskować, że jest on również kwadratem wystarczy zauważyć, że OA=OB - oba te odcinki są promieniami okręgu w.
Zadanie 14
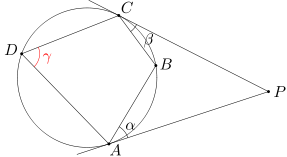
Czworokąt wypukły ABCD, o kącie ostrym przy wierzchołku D, jest wpisany w okrąg. Styczne do tego okręgu w punktach A i C przecinają się w punkcie P. Wiedząc, że miara kąta BAP wynosi α, a miara kąta BCP wynosi β, oblicz miarę kąta ADC.
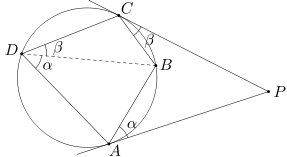
Korzystając z twierdzenia o kącie między styczną a cięciwą wnioskujemy, że miary kątów BAP i BDA są równe. Podobnie uzyskujemy równość kątów BCP i BDC. Stąd
\(\angle ADC=\angle BDA+\angle BDC=\angle BAP+\angle BCP=\alpha+\beta.\)
Zadanie 15
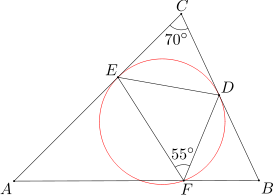
Dany jest trójkąt ABC, w którym miara kąta przy wierzchołku C równa się 70 stopni. Punkty D, E, F leżą odpowiednio na bokach BC, CA, AB, przy czym CE=CD oraz miara kąta DFE wynosi 55 stopni. Wykaż, że okrąg opisany na trójkącie DEF jest styczny do prostych BC i CA.
Zadanie 16
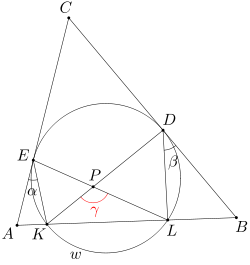
Dany jest trójkąt ABC. Okrąg w jest styczny do boków BC, CA odpowiednio w punktach D, E oraz przecina odcinek AB w punktach K, L (przyjmujemy, że punkty K, L, D, E leżą w tej właśnie kolejności na okręgu w). Odcinki KD i EL przecinają się w punkcie P. Wiedząc, że miara kąta AEK wynosi α, a miara kąta BDL wynosi β, oblicz miarę kąta KPL.
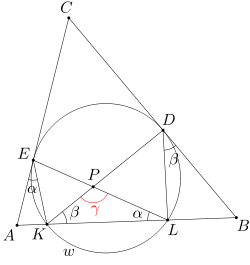
Korzystając z twierdzenia o kącie między styczną a cięciwą wnioskujemy, że miary kątów AEK i ELK są równe. Podobnie, miary kątów BDL i DKL są równe. Stąd uzyskujemy
\(\angle ELK+\angle DKL=\angle AEK+\angle BDL=\alpha+\beta.\)
Wobec tego
\(\angle KPL=180^\circ-\alpha-\beta\).
Zadanie 17
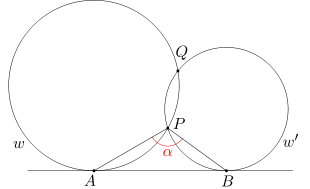
Okręgi w oraz w' przecinają się w punktach P i Q. Do okręgów w oraz w' poprowadzono wspólną styczną zewnętrzną AB (przyjmujemy, że styczna ta leży bliżej punktu P niż punktu Q). Wiedząc, że długość łuku AP stanowi 1/6 długości łuku okręgu w, a długość łuku PB stanowi 1/5 długości okręgu w', oblicz miarę kąta APB.
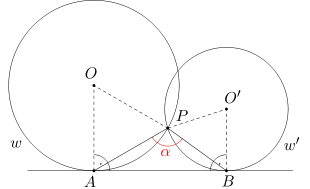
Oznaczmy przez O i O' odpowiednio środki okręgów w i w'. Ponieważ łuk AP okręgu w stanowi 1/6 długości okręgu w, więc kąt AOP ma miarę 360:6=60 stopni. Ponieważ trójkąt AOP jest równoramienny (odcinki OA i OP są promieniami okręgu w), więc miara kąta OAP równa się (180-60)/2=60 stopni.
Odcinek OA jest prostopadły do prostej AB, gdyż prosta AB jest styczna do okręgu w w punkcie A. Wobec tego miara kąta PAB wynosi 90-60=30 stopni.
Analogicznie obliczamy miarę kąta PBA: Ponieważ łuk PB okręgu w' stanowi 1/5 długości łuku okręgu w', więc kąt PO'B ma miarę 360:5=72 stopnie. Trójkąt PO'B jest równoramienny (odcinki O'P i O'B są promieniami okręgu w'), skąd wynika, że miara kąta O'BP równa się (180-72)/2=54 stopnie.
Odcinek O'B jest prostopadły do prostej AB, gdyż prosta AB jest styczna do okręgu w' w punkcie B. Wobec tego miara kąta PBA wynosi 90-54=36 stopni.
Stąd ostatecznie miara kąta APB równa się 180-36-30=114 stopni.
Zadanie 18
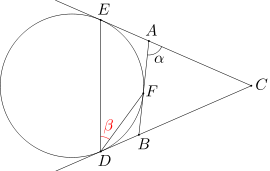
Dany jest trójkąt ABC. Okrąg dopisany do trójkąta ABC jest styczny do boku AB w punkcie F, a do prostych zawierających boki BC i AC odpowiednio w punktach D i E. Wiedząc, że miara kąta BAC wynosi α, wyznacz miarę kąta EDF.
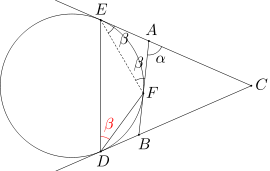
Ponieważ AE=AF, więc miara kąta AEF równa się mierze kąta AFE. Wobec tego miara kąta AEF wynosi α / 2.
Na mocy twierdzenia o kącie miedzy styczną a cięciwą, miara kąta EDF równa się mierze kąta AEF, czyli α / 2.
Zadanie 19
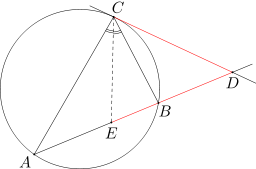
Okrąg w jest opisany na trójkącie ABC. Styczna do okręgu w w punkcie C przecina prostą AB w punkcie D. Dwusieczna kąta ACB przecina bok AB w punkcie E. Wykaż, że długości odcinków CD i DE są równe.
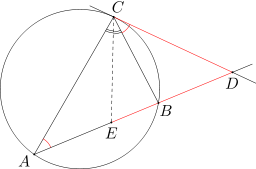
Korzystając z twierdzenia o kącie między styczną a cięciwą otrzymujemy
\(\angle ECD=\angle ECB+\angle BCD= \angle ACE+\angle CAB=\angle CED.\)
Stąd wynika, że odcinki CD i DE są równej długości.
Zadanie 20
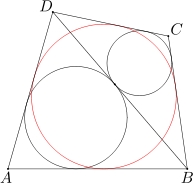
Dany jest czworokąt wypukły ABCD. Udowodnij, że jeśli okręgi wpisane w trójkąty ABD i BCD są styczne do odcinka BD w tym samym punkcie, to w czworokąt ABCD można wpisać okrąg.
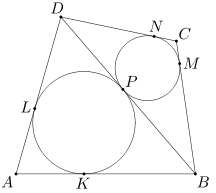
Przyjmijmy, że okręgi wpisane w trójkąty ABD i BCD są styczne do odcinka BD w punkcie P. Niech ponadto okrąg wpisany w trójkąt ABD będzie styczny do boków AB i AD odpowiednio w punktach K i L. Analogicznie, przyjmijmy, że okrąg wpisany w trójkąt BCD jest styczny do boków BC i CD odpowiednio w punktach M i N.
Wówczas uzyskujemy AK=AL, CN=CM, BK=BP=BM oraz DN=DP=DL. Z równości tych dostajemy
AB+CD=AK+BK+CN+DN=AL+BM+CM+DL=AD+BC.
Z otrzymanej równości wynika bezpośrednio, że w czworokąt ABCD można wpisać okrąg.
