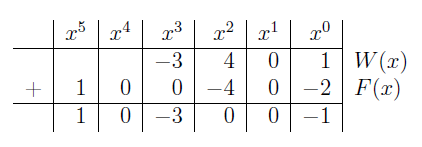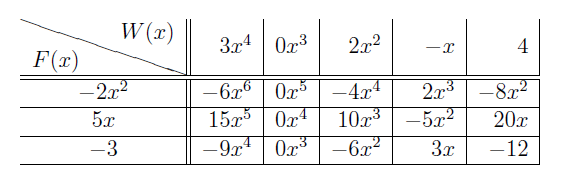Skip to Content

Działania na wielomianach

pt., 09/10/2010 - 10:32 — ciebie


2. Działania na wielomianach

Wielomiany zmiennej \(x\;\), jako jednomiany lub ich sumy, można dodawać i odejmować. W wyniku tych działań, po ewentualnej redukcji wyrazów podobnych, otrzymujemy znów jednomiany lub ich sumy czyli wielomiany. Zatem sumy i różnice wielomianów zmiennej \(x\;\) są także wielomianami zmiennej \(x\;\).

Przykłady:
  1. Niech \(W(x) = -3x^3+4x^2+1\;\) i \(F(x) = x^5-4x^2-2\;\).
    Wówczas
    \(\begin{array}{rl} W(x)+F(x) & = -3x^3\underline{+4x^2}\; \underline{\underline{+1}} + x^5 \underline{-4x^2}\; \underline{\underline{-2}} = x^5-3x^3-1,\\ W(x)-F(x) & = -3x^3+4x^2 + 1 - (x^5-4x^2-2)=\\ & = -3x^3\underline{+4x^2}\; \underline{\underline{+1}} - x^5 \underline{+4x^2}\; \underline{\underline{+2}}=\\ & =-x^5-3x^3+8x^2+3. \end{array}\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=3\;\), \(\mathrm{st}\, F(x)=5\;\), \(\mathrm{st}\big (W(x)+F(x)\big )=5\;\), \(\mathrm{st}\big (W(x)-F(x)\big )=5\;\).
  2. Niech \(W(x) = -x^3+x\;\) i \(F(x)=x^3+x^2-x+1\;\).
    Wówczas
    \(\begin{array}{rl} W(x)+F(x) & = \underline{-x^3}\; \underline{\underline{+x}}\; \underline{+x^3}+x^2\; \underline{\underline{-x}}+1 = x^2+1,\\ W(x)-F(x) & = \underline{-x^3}\; \underline{\underline{+x}}\; \underline{-x^3}-x^2\; \underline{\underline{+x}}-1 = -2x^3-x^2+2x-1. \end{array}\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=3\;\), \(\mathrm{st}\, F(x)=3\;\), \(\mathrm{st}\big (W(x)+F(x)\big )=2\;\), \(\mathrm{st}\big (W(x)-F(x)\big )=3\;\).
  3. Niech \(W(x)=x^4-x+2\;\) i \(F(x)=-x^4+x-2\;\).
    Wówczas
    \(\begin{array}{rl} W(x)+F(x) & = \underline{x^4}\; \underline{\underline{-x}} + 2 + \underline{(-x^4)}\; \underline{\underline{+x}} -2 = 0,\\ W(x)-F(x) & = x^4 - x + 2 - (-x^4 + x - 2) = \underline{x^4}\; \underline{\underline{-x}}+2\; \underline{+x^4}\; \underline{\underline{-x}}+2 = 2x^4-2x+4. \end{array}\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=4\;\), \(\mathrm{st}\, F(x)=4\;\), \(W(x)+F(x)\;\) jest wielomianem zerowym, \(\mathrm{st}\big (W(x)-F(x)\big )=4\;\).
  4. Niech \(W(x)=5x^6-2x^5+x+2\;\) i \(F(x)=0\;\).
    Wówczas
    \(\begin{array}{rl} W(x)+F(x) & = 5x^6-2x^5+x+2 + 0 = W(x),\\ W(x)-F(x) & = 5x^6-2x^5+x+2 - 0 = W(x),\\ F(x)-W(x) & = 0 - (5x^6-2x^5+x+2) = -5x^6+2x^5-x-2. \end{array}\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=6\;\), \(F(x)\;\) jest wielomianem zerowym, \(\mathrm{st}\big (W(x)+F(x)\big )=6\;\),\(\mathrm{st}\big (W(x)-F(x)\big )=6\;\), \(\mathrm{st}\big (F(x)-W(x)\big )=6\quad\;\)

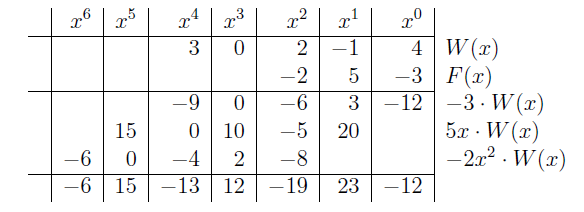
Uwaga 2.1. Dodawanie i odejmowanie wielomianów sprowadza się do pewnych operacji na współczynnikach. Można je zapisać w sposób analogiczny do operacji pisemnego dodawania i odejmowania liczb naturalnych. Obliczenia z przykładu 1. można zapisać następująco:

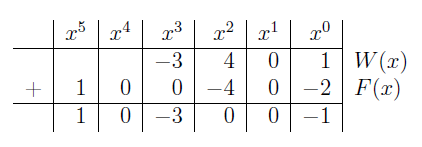
Z ostatniego wiersza tabeli odczytujemy \(W(x)+F(x) = x^5-3x^3-1\;\).

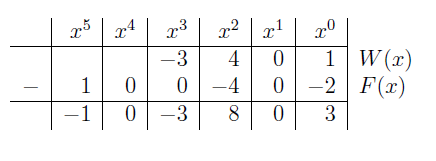
Image:tabelkaT12.png

Z ostatniego wiersza tabeli odczytujemy \(W(x)-F(x) = -x^5-3x^3+8x^2+3\;\).

Ta obserwacja pozwala dostrzec podobieństwa między dodawaniem i odejmowaniem liczb oraz dodawaniem i odejmowaniem wielomianów. Nie jest ważna kolejność sumowanych wielomianów. W sumach kilku wielomianów można przestawiać składniki i łączyć je w grupy, a prawidłowość wykonania odejmowania wielomianów można sprawdzić przez dodanie wyniku odejmowania do odjemnika.

Image:End_of_proof.gif

Odwołując się do mechanizmu tworzenia sumy i różnicy wielomianów zmiennej \(x\;\), można sformułować twierdzenie.

Twierdzenie 2.1.:
  1. Suma i różnica wielomianów niezerowych jest albo wielomianem zerowym, albo ma stopień nie większy niż największy ze stopni wielomianów, na których wykonujemy działanie.
  2. Suma i różnica wielomianów zerowych jest wielomianem zerowym.
  3. Wielomian będący sumą lub różnicą dwóch wielomianów, z których tylko jeden jest niezerowy, ma ten sam stopień co rozważany wielomian niezerowy.
Image:End_of_proof.gif

Wielomiany będące jednomianami lub sumami jednomianów mnożymy zgodnie z zasadami mnożenia sum algebraicznych. Ponieważ iloczyn jednomianów jest jednomianem, więc w wyniku mnożenia wielomianów uzyskujemy jednomiany lub ich sumy, czyli wielomiany.

Przykłady:
  1. Niech \(W(x) = 2x^5-x^2+1\;\) i \(F(x)=x^3-2x\;\).
    Wówczas
    \(\begin{array}{rl} W(x)\cdot F(x) & = (2x^5-x^2+1)(x^3-2x)=\\ & = 2x^8-4x^6-x^5+2x^3+x^3-2x=\\ & = 2x^8-4x^6-x^5+3x^3-2x. \end{array}\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=5\;\), \(\mathrm{st}\, F(x)=3\;\), \(\mathrm{st}\big (W(x)\cdot F(x)\big )=8 = \mathrm{st}\, W(x)+\mathrm{st}\, F(x)\;\).
  2. Niech \(W(x)=x^{100}-1\;\) i \(F(x)=x^2+4\;\).
    Wówczas
    \(W(x)\cdot F(x) = (x^{100}-1)(x^2+4) = x^{102}+4x^{100}-x^2-4.\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=100\;\), \(\mathrm{st}\, F(x)=2\;\), \(\mathrm{st}\big (W(x)\cdot F(x)\big )= 102 = \mathrm{st}\, W(x)+\mathrm{st}\, F(x)\;\).
  3. Niech \(W(x)=7\;\) i \(F(x)=x^3+3x\;\).
    Wówczas
    \(W(x)\cdot F(x) = 7(x^3+3x) = 7x^3+21x.\;\)
    Zauważmy, że \(\mathrm{st}\, W(x)=0\;\), \(\mathrm{st}\, F(x)=3\;\), \(\mathrm{st}\big (W(x)\cdot F(x)\big )= 3 = \mathrm{st}\, W(x)+\mathrm{st}\, F(x)\;\).
  4. Niech \(W(x)=-1\;\) i \(F(x)=4x^3-2x^7+x-5\;\).
    Wówczas
    \(W(x)\cdot F(x) = (-1)(4x^3-2x^2+x-5) = -4x^3+2x^2-x+5.\;\)
    Zamiast \((-1)F(x)\;\) piszemy \(-F(x)\;\). Zauważmy, że \(\mathrm{st}\, W(x)=0\;\), \(\mathrm{st}\, F(x)=3\;\), \(\mathrm{st}\big (W(x)\cdot F(x)\big )=3=\mathrm{st}\, W(x)+\mathrm{st}\, F(x)\;\).
  5. Niech \(W(x)=0\;\) i \(F(x)=x^{1000}+2x^2+x-1\;\).
    Wówczas
    \(W(x)\cdot F(x) = 0(x^{1000}+2x^2+x-1)=0,\;\)
    czyli iloczyn jest wielomianem zerowym.

Uwaga 2.2. Mnożenie wielomianów również sprowadza się do pewnych operacji na współczynnikach. Można je powiązać z mnożeniem pisemnym liczb naturalnych, chociaż analogia jest może trudniejsza do dostrzeżenia.

Niech \(W(x) = 3x^4+2x^2-x+4\;\), \(F(x) = -2x^2+5x-3\;\).

Image:tabelkaT13.png

Interpretacja wyniku w tabeli jest następująca:

\(W(x)\cdot F(x) = -6x^6 +15x^5-13x^4+12x^3-19x^2+23x-12.\;\)

Innym sposobem mnożenia wielomianów jest następująca procedura zademonstrowana na przykładzie wielomianów \(W(x)=3x^4+2x^2-x+4\;\) i \(F(x)=-2x^5+5x-3\;\).

1. Rozpisujemy oba uporządkowane wielomiany w tabeli umieszczając jednomiany jednego z nich w wierszu, a drugiego w kolumnie.

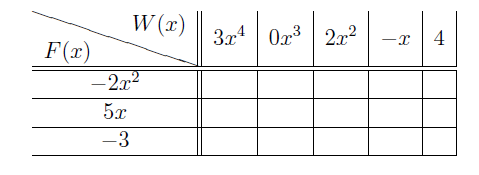
Image:tabelkaT14.png

2. Wypełniamy wolne pola tabeli wpisując iloczyny jednomianów występujące w odpowiednich wierszu i kolumnie.

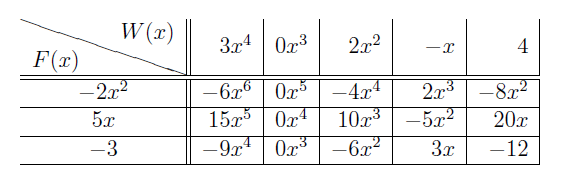
Image:tabelkaT15.png

3. Dostrzegamy, że na "przekątnych" powstają jednomiany z tą samą potęgą zmiennej. 4. Sumujemy jednomiany o wspólnej potędze zmiennej i dokonujemy redukcji. 5. Suma otrzymanych w taki sposób jednomianów daje wielomian \(W(x)\cdot F(x)=-6x^6 + 15x^5 -13x^4 + 12x^3 - 19 x^2 +23x-12\;\)

Image:End_of_proof.gif

Rozumiejąc mechanizm tworzenia iloczynu wielomianów, łatwo sobie uświadomić, że podobnie jak w przypadku mnożenia liczb, przy mnożeniu wielomianów nie jest ważna kolejność czynników. Można też w sytuacji mnożenia kilku wielomianów przez siebie przestawiać je i łączyć w pary, co może ułatwić rachunki.

Przykład 2.3.:

Niech \(W(x)=x-2\;\), \(P(x)=2x^2+3\;\), \(R(x)=x+2\;\). Zamiast liczyć iloczyn \(W(x)\cdot P(x)\cdot R(x)\;\) w podanej kolejności, można obliczyć \(\big (W(x)\cdot R(x)\big )\cdot P(x)\;\).
\(\begin{array}{rl} W(x)\cdot P(x)\cdot R(x) & = \big (W(x)\cdot R(x)\big )\cdot P(x) = \big ((x-2)(x+2)\big )(2x^2+3)=\\ & = (x^2-4)(2x^2+3) = 2x^4+3x^2-8x^2-12 = 2x^4-5x^2-12. \end{array}\;\)

Jeszcze raz odwołując się do mechanizmu tworzenia iloczynu wielomianów, można sformułować twierdzenie.

Twierdzenie 2.2.:
  1. Stopień iloczynu dwóch wielomianów niezerowych jest sumą stopni wielomianów występujących w iloczynie.
  2. Iloczyn wielomianu zerowego przez dowolny wielomian jest wielomianem zerowym.


Theme by Dr. Radut.