Processing math: 100%
Skip to Content

Funkcje wielomianowe

pt., 09/10/2010 - 11:56 — ciebie

8. Funkcje wielomianowe

Wielomiany są to pewne szczególne wyrażenia algebraiczne. W postaci uporządkowanej opisane są przy pomocy wzoru
W(x)=anxn+an−1xn−1+…+a1x+a0,
gdzie n jest ustaloną liczbą całkowitą nieujemną, a0,a1,…,an są ustalonymi liczbami rzeczywistymi. Za zmienną x można podstawić dowolną liczbę rzeczywistą x0 i otrzymana w ten sposób liczba anxn0+an−1xn−10+…+a1x0+a0 nazywa się wartością wielomianu dla x=x0.

Wśród wielomianów wyróżnia się między innymi

  • wielomian zerowy, który dla każdej liczby x0 przyjmuje wartość 0,
  • wielomiany stopnia zerowego przyjmujące tę samą wartość, różną od 0, dla wszystkich liczb rzeczywistych podstawionych za zmienną,
  • wielomiany stopnia pierwszego, postaci W(x)=a1x+a0, gdzie a0,a1 są ustalonymi liczbami rzeczywistymi i a1≠0,
  • wielomiany stopnia drugiego, postaci W(x)=a2x2+a1x+a0, gdzie a0,a1,a2 są ustalonymi liczbami rzeczywistymi i a2≠0.

Z wymienionymi wyżej wielomianami spotykamy się w nauczaniu szkolnym matematyki znacznie wcześniej niż z pojęciem wielomianu. Pierwsze trzy wielomiany poznaje się w trakcie nauki o funkcji liniowej, a ostatni przy omawianiu funkcji kwadratowej.

Funkcja liniową nazywamy funkcję f określoną w zbiorze liczb rzeczywistych, przyjmującą wartości rzeczywiste (f:R→R), zadaną dla każdego argumentu x∈R wzorem f(x)=ax+b, gdzie a,b sa ustalonymi liczbami rzeczywistymi. Wyrażenie algebraiczne ax+b opisujące sposób obliczania wartości funkcji f dla argumentu x jest

  • wielomianem zerowym, jeśli a=0 i b=0,
  • wielomianem stopnia zerowego, jeśli a=0 i b≠0,
  • wielomianem stopnia pierwszego, gdy a≠0 i b∈R.

Funkcją kwadratową nazywamy funkcję g określoną w zbiorze liczb rzeczywistych, przyjmującą wartości rzeczywiste (g:R→R), zadaną dla każdego argumentu x∈R wzorem g(x)=ax+bx+c, gdzie a,b,c sa ustalonymi liczbami rzeczywistymi i a≠0. Wyrażenie algebraiczne ax2+bx+c opisujące sposób obliczania wartości funkcji g dla liczby x jest wielomianem drugiego stopnia.

Naturalne jest wprowadzenie następującej definicji

Definicja 8.1. Funkcję h określoną w zbiorze liczb rzeczywistych, przyjmującą wartości rzeczywiste (h:R→R), zadaną dla każdego argumentu x∈R wzorem
h(x)=anxn+an−1xn−1+…+a1x+a0,
gdzie n jest ustaloną liczbą całkowitą nieujemną i a0,a1,…,an sa ustalonymi liczbami rzeczywistymi nazywamy funkcją wielomianową. Jeśli an≠0, to mówimy, że funkcja h jest funkcją wielomianową stopnia n.

Uwaga 8.1. Wykresy funkcji wielomianowych są zróżnicowane. Wykresem każdej funkcji liniowej jest prosta, a wykresem kwadratowej - parabola. Wykresy funkcji wielomianowych stopnia wyższego niż 2 mają bardzo rozmaite kształty. Poniżej podajemy kilka przykładów.

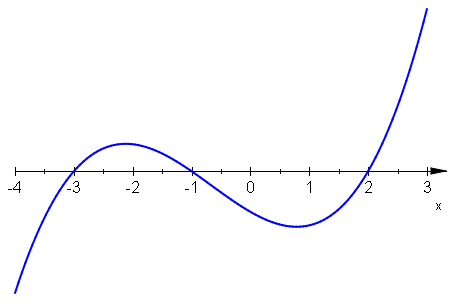
  • f1(x)=(x+3)(x+1)(x−2), czyli f1(x)=x3+2x2−5x−6,
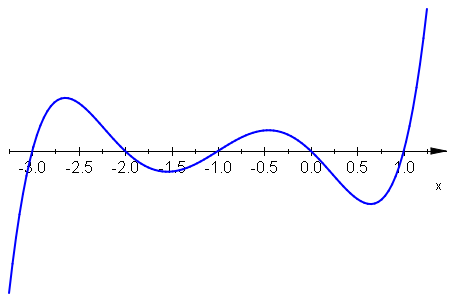
  • f2(x)=(x+3)(x+2)(x+1)x(x−1), czyli f2(x)=x5+5x4+5x3−5x2−6x,
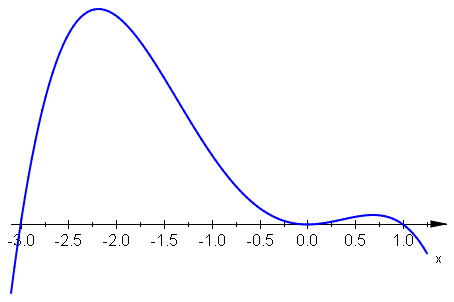
  • f3(x)=−2x2(x−1)(x+3), czyli f3(x)=−2x4−4x3+6x2,
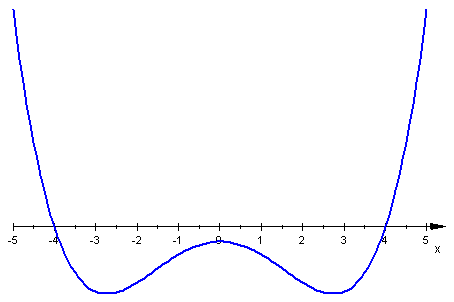
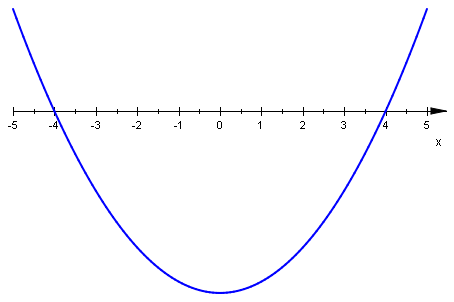
  • f4(x)=(x2+1)(x−4)(x+4), czyli f4(x)=x4−15x2−16,
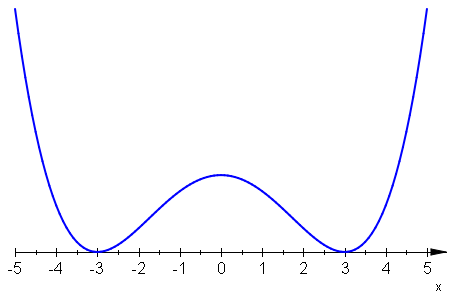
  • f5(x)=(x−3)2(x+3)2, czyli f5(x)=x4−18x2+81,
  • f6(x)=(x−1)(x+2)(6x2+1), czyli f6(x)=6x4+6x3−11x2+x−2.


f1(x)=(x+3)(x+1)(x−2)

f2(x)=(x+3)(x+2)(x+1)x(x−1)

f3(x)=−2x2(x−1)(x+3)

f4(x)=(x2+1)(x−4)(x+4)

f5(x)=(x−3)2(x+3)2

f6(x)=(x−1)(x+2)(6x2+1)

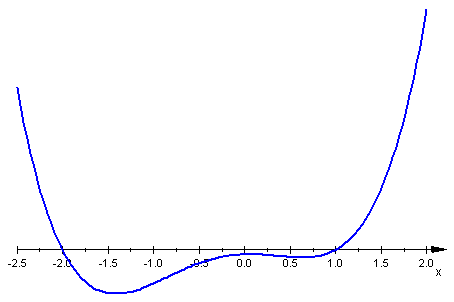Porównajmy wykresy funkcji f1−f6 z "wykresami znaków" wielomianów określających te funkcje (patrz Nierówności wielomianowe Metoda II). Korzystamy z postaci iloczynowej każdego z wielomianów.


f1(x)=(x+3)(x+1)(x−2)

f2(x)=(x+3)(x+2)(x+1)x(x−1)

f3(x)=−2x2(x−1)(x+3)

f4(x)=(x2+1)(x−4)(x+4)

f5(x)=(x−3)2(x+3)2

f6(x)=(x−1)(x+2)(6x2+1)

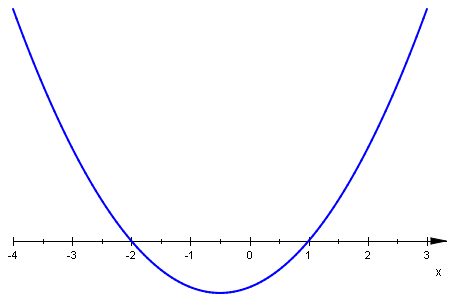W przypadku funkcji f1, f2, f3, f5 wykresy funkcji i "wykresy znaków" wielomianów są bardzo podobne. "Wykresy znaków" wielomianów dobrze przybliżają nam zarys wykresów funkcji, są jak gdyby jej szkicami. Będzie tak zawsze, gdy w rozkładzie wielomianu jedynymi czynnikami nierozkładalnymi są czynniki liniowe.

"Wykresy znaków" wielomianów opisujących funkcje f4 i f6 istotnie różnią się kształtem od wykresów funkcji. W przypadku funkcji f4 decyduje o tym czynnik x2+1 pojawiający się w postaci iloczynowej wielomianu; w przypadku funkcji f6 czynnik 6x2+1.

Prawidłowa jest intuicja:

"Wykres znaków" wielomianu W(x) stanowi pewne przybliżenie wykresu funkcji wielomianowej y=W(x). Nie może być jednak traktowany jako wykres funkcji.

∎

Uwaga 8.2. Porównajmy wykresy funkcji

  • g1(x)=−3(x+3)(x+1)(x−2),
  • g2(x)=−3(x+3)(x+1)(x−2)2,
  • g3(x)=−3(x+3)(x+1)(x−2)3,
  • g4(x)=−3(x+3)(x+1)(x−2)4.

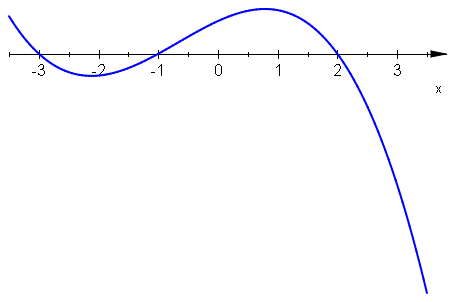
"Wykresy znaków" wielomianów −3(x+3)(x+1)(x−2) i −3(x+3)(x+1)(x−2)3 przedstawia krzywa


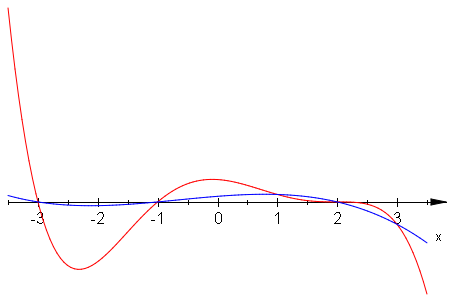
Różnicę wykresów funkcji g1 i g3 przedstawia rysunek


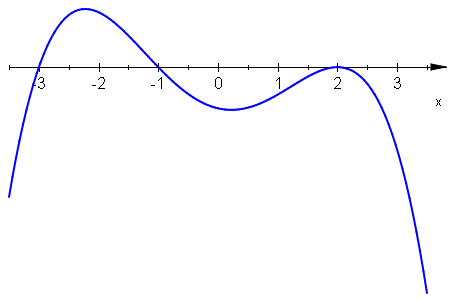
Podobnie "wykresy znaków" wielomianów −3(x+3)(x+1)(x−2)2 i −3(x+3)(x+1)(x−2)4 przedstawia krzywa


Różnicę wykresów funkcji g2 i g4 przedstawia rysunek


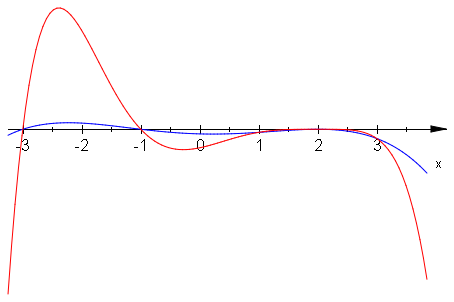Dla wielomianów, które mają "wyższą krotność" pierwiastka, punkty wykresu "w pobliżu punktu (2,0)" znajdują się bliżej osi OX.

∎



Theme by Dr. Radut.