Definicja 7.1: Nierównością wielomianową nazywamy każdą nierówność postaci
\(
W(x)>0,\quad W(x)<0,\quad W(x)\geq 0,\quad W(x)\leq 0,
\;\)
gdzie \(W(x)\;\) jest wielomianem. Nierówność wielomianowa jest stopnia \(n\;\) jeżeli wielomian \(W(x)\;\) występujący w którejś z wymienionych wyżej nierówności jest stopnia \(n\;\).
Definicja 7.2: Zbiorem rozwiązań nierówności wielomianowej nazywamy zbiór wszystkich liczb spełniających tę nierówność.
Zwracamy uwagę na to, że rozwiązywanie nierówności wielomianowej, np. \(W(x)>0\;\), możemy potraktować jako znajdowanie wszystkich liczb rzeczywistych, dla których wartości wielomianu \(W(x) \;\) są dodatnie.
Do rozwiązywania nierówności stopni wyższych niż \(2\;\) przydaje się znajomość sposobów rozwiązywania nierówności liniowych i kwadratowych. Podstawowe informacje przypominają następujące przykłady.
Przykład 1. (\(W(x)\;\) jest wielomianem zerowym): Nierówności \(W(x)>0\;\), \(W(x)<0\;\) mają pusty zbiór rozwiązań; natomiast zbiorem rozwiązań nierówności \(W(x)\geq 0\;\) i \(W(x)\leq 0\;\) jest zbiór wszystkich liczb rzeczywistych.
Przykład 2. \(W(x)\;\) jest wielomianem stopnia zerowego): Niech \(c\;\) będzie liczbą rzeczywistą różną od \(0\;\) i niech \(W(x)=c\;\) dla wszystkich \(x\in\mathbb{R}\;\). Jeśli \(c>0\;\), to zbiorem rozwiązań
- \(W(x)>0\;\) jest zbiór wszystkich liczb rzeczywistych,
- \(W(x)<0\;\) jest zbiór pusty,
- \(W(x)\geq0\;\) jest zbiór wszystkich liczb rzeczywistych,
- \(W(x)\leq0\;\) jest zbiór pusty.
W przypadku \(c<0\;\) można sformułować podobne stwierdzenie.
Przykład 3. (\(W(x)\;\) jest wielomianem stopnia pierwszego): Niech wielomian \(W(x)\;\) będzie postaci \(W(x)=ax+b\;\), gdzie \(a,b\in\mathbb{R}\;\) i \(a\ne 0\;\). Zbiorem rozwiązań
- nierówności \(ax+b>0\;\) jest
- przedział \(\left(-\frac{b}{a},+\infty\right)\;\), gdy \(a>0\;\),
- przedział \(\left(-\infty,-\frac{b}{a}\right)\;\), gdy \(a<0\;\),
- nierówności \(ax+b\geq0\;\) jest
- przedział \(\langle-\frac{b}{a},+\infty)\;\), gdy \(a>0\;\),
- przedział \(\left(-\infty,-\frac{b}{a}\right\rangle\;\), gdy \(a<0\;\),
- nierówności \(ax+b<0\;\) jest
- przedział \(\left(-\infty,-\frac{b}{a}\right)\;\), gdy \(a>0\;\),
- przedział \(\left(-\frac{b}{a},+\infty\right)\;\), gdy \(a<0\;\),
- nierówności \(ax+b>0\;\) jest
- przedział \(\left(-\infty,-\frac{b}{a}\right\rangle\;\), gdy \(a>0\;\),
- przedział \(\left\langle-\frac{b}{a},+\infty\right)\;\), gdy \(a<0\;\).
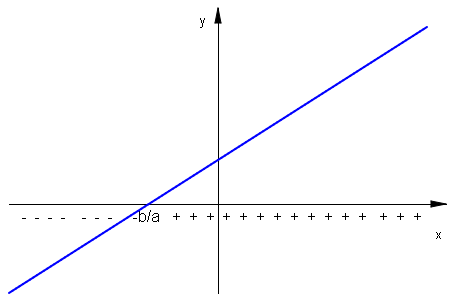
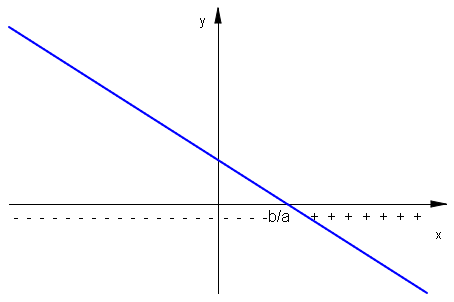
Zbiór rozwiązań nierówności pierwszego stopnia można odczytać z wykresu funkcji \(f(x)=ax+b\;\).
| \( a>0\;\) | \( a<0\;\) |
 |
 |
Przykład 4. (Wielomian \(W(x)\;\) jest wielomianem stopnia drugiego): Niech \(W(x)=ax^2+bx+c\;\) i \(a\ne 0\;\). Są dwa sposoby rozwiązywania nierówności kwadratowej.
I Metoda algebraiczna. W zależności od znaku wyróżnika \(\Delta =b^2-4ac\;\) postępujemy w zróżnicowany sposób.
Przypadek 1. \(W(x)=ax^2+bx+c\;\), \(a\ne0\;\) i \(\Delta>0\;\).
Trójmian kwadratowy \(W(x)=ax^2+bx+c\;\) można zapisać w postaci iloczynowej \(a(x-x_1)(x-x_2)\;\), gdzie \(x_1,x_2\;\) sa jego dwoma różnymi pierwiastkami.
Nierówność \(W(x)>0\;\) czyli \(a(x-x_1)(x-x_2)>0\;\) jest równoważna alternatywie
\(
\left\{\begin{array}{l}
a(x-x_1)>0\\
x-x_2>0
\end{array}\right.,\quad\mathrm{lub}\quad
\left\{\begin{array}{l}
a(x-x_1)<0\\
x-x_2<0
\end{array}\right..
\;\)
Rozwiązując każdy z układów nierówności i biorąc sumę ich rozwiązań otrzymujemy zbiór rozwiązań nierówności \(W(x)>0\;\).
Nierówność \(W(x)\geq0\;\) czyli \(a(x-x_1)(x-x_2)\geq0\;\) zastępujemy analogiczną alternatywą warunków
\(
\left\{\begin{array}{l}
a(x-x_1)\geq0\\
x-x_2\geq0
\end{array}\right.,\quad\mathrm{lub}\quad
\left\{\begin{array}{l}
a(x-x_1)\leq0\\
x-x_2\leq0
\end{array}\right.
\;\)
i dalej postępujemy podobnie.
Nierówność \(W(x)<0\;\) (\(W(x)\leq0\;\)) można sprowadzić do analogicznego przypadku mnożąc nierówność przez \((-1)\;\), lub zastąpić je warunkami równoważnymi
\(
\left\{\begin{array}{l}
a(x-x_1)>0\\
x-x_2<0
\end{array}\right.,\quad\mathrm{lub}\quad
\left\{\begin{array}{l}
a(x-x_1)<0\\
x-x_2>0
\end{array}\right.,
\;\)
\( \left( \left\{\begin{array}{l} a(x-x_1)\geq0\\ x-x_2\leq0 \end{array}\right.,\quad\mathrm{lub}\quad \left\{\begin{array}{l} a(x-x_1)\leq0\\ x-x_2\geq0 \end{array}\right. \right). \;\)
Przypadek 2. \(W(x)=ax^2+bx+c\;\), \(a\ne0\;\) i \(\Delta=0\;\).
Trójmian kwadratowy \(W(x)=ax^2+bx+c\;\) ma postać iloczynową \(a(x-x_0)^2\quad\;\), gdzie \(x_0\;\) jest jedynym jego pierwiastkiem.
Zbiorem rozwiązań
- nierówności \(a(x-x_0)^2>0\;\) jest \(\mathbb{R}\setminus\{0\}\;\), gdy \(a>0\;\) i \(\emptyset\;\) gdy \(a<0\;\),
- nierówności \(a(x-x_0)^2\geq0\;\) jest \(\mathbb{R}\;\), gdy \(a>0\;\) i \(\{x_0\}\;\) gdy \(a<0\;\),
- nierówności \(a(x-x_0)^2<0\;\) jest \(\emptyset\;\), gdy \(a>0\;\) i \(\mathbb{R}\setminus\{0\}\;\), gdy \(a<0\;\),
- nierówności \(a(x-x_0)^2\leq0\;\) jest \(\{x_0\}\;\), gdy \(a>0\;\) i \(\mathbb{R}\;\), gdy \(a<0\;\).
Przypadek 3. \(W(x)=ax^2+bx+c\;\), \(a\ne0\;\) i \(\Delta<0\;\).
W tym przypadku trójmian kwadratowy ma postać kanoniczną
\(
W(x) = a(x-x_w)^2+y_w \quad\mathrm{i}\quad a\cdot y_w>0,
\;\)
gdzie \((x_w,y_w)\;\) wskazuje współrzędne wierzchołka paraboli opisanej przez ten trójmian.
W przypadku \(a>0\;\) funkcja \(f(x)=ax^2+bx+c\;\) przyjmuje tylko wartości dodatnie. Zatem dla \(a>0\;\) zbiorem rozwiązań
- nierówności \(W(x)>0\;\) jest zbiór \(\mathbb{R}\;\),
- nierówności \(W(x)\geq0\;\) jest zbiór \(\mathbb{R}\;\),
- nierówności \(W(x)<0\;\) jest zbiór \(\emptyset\;\),
- nierówności \(W(x)\leq0\;\) jest zbiór \(\emptyset\;\).
Podobne stwierdzenie można wyprowadzić, gdy \(a<0\;\).
II Metoda graficzna (w oparciu o wykres funkcji kwadratowej).
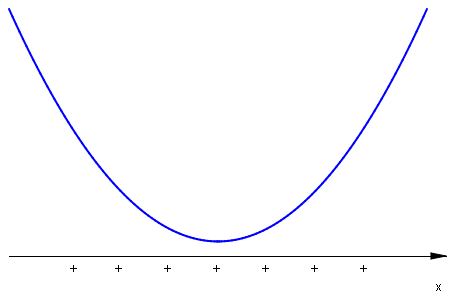
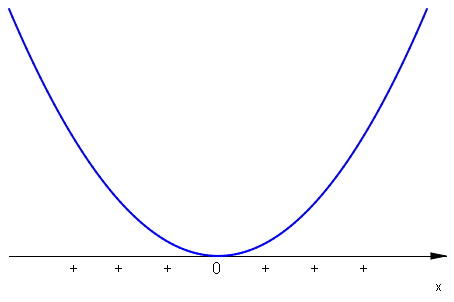
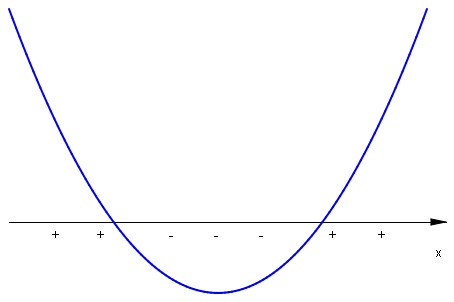
Z wykresu funkcji \(f:\mathbb{R}\rightarrow\mathbb{R}\;\), \(f(x)=ax^2+bx+c\;\) można odczytać zbiór rozwiązań nierówności \(f(x)>0\;\), \(f(x)\geq 0\;\), \(f(x)<0\;\), \(f(x)\leq 0\;\). W przypadku \(a>0\;\) mamy np. dla nierówności \(W(x)>0\;\) rozwiązanie
 |
 |
 |
|
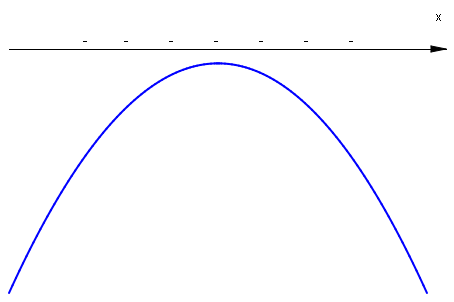
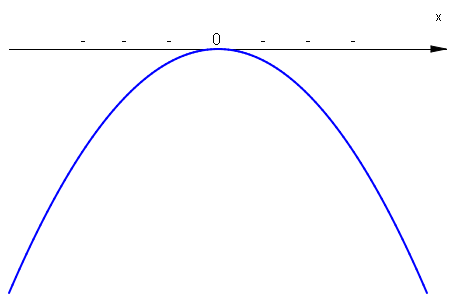
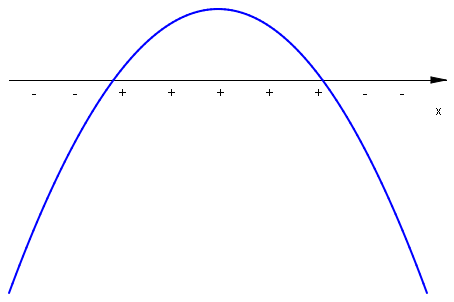
W przypadku \(a<0\;\) mamy dla nierówności \(W(x)>0\;\) rozwiązanie
 |
 |
 |
|
Analogicznie można opisać zbiory rozwiązań nierówności \(ax^2+bx=c\geq 0\;\).
Rozważmy teraz nierówności wielomianowe stopnia wyższego niż 2. Podstawą metod zaprezentowanych poniżej jest spostrzeżenie, że jeśli wielomian \(W(x)\;\) występujący w nierówności \(W(x)>0\;\) (\(W(x)<0\;\), \(W(x)\geq0\;\), \(W(x)\leq0\;\)) jest w postaci iloczynowej, zawierającej tylko czynniki liniowe i kwadratowe z wyróżnikiem ujemnym (patrz Twierdzenie 5.7. i Twierdzenie 5.8), to taką nierówność łatwo rozwiązać przez analizę znaków każdego z czynników.
Metoda 1. (Tabela znaków) Sposób rozwiązywania nierówności przedstawimy w kolejnych 2 zadaniach.
Zadanie 7.1: Rozwiąż nierówność \((x-2)(x+3)(5-x)<0\;\).
Rozwiązanie: Zauważmy, że potrafimy podać znaki każdego z czynników
| \(x-2\qquad\;\) | 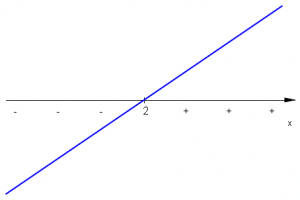 |
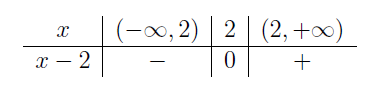 |
| \(x+3\qquad\;\) | 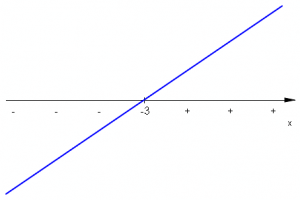 |
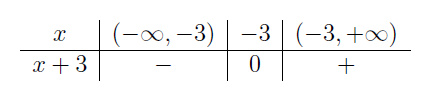 |
| \(5-x\qquad\;\) | 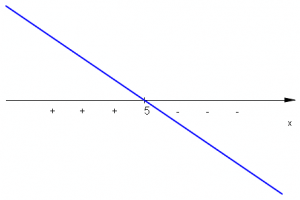 |
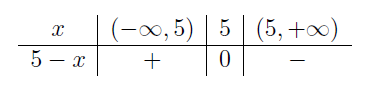 |
Umieszczamy te informacje w jednej tabeli.
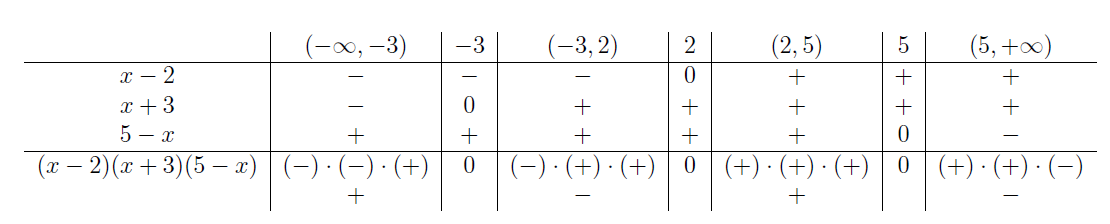
Znak iloczynu otrzymujemy "wymnażając" znaki w odpowiednich kolumnach.
Zbiorem rozwiązań nierówności \((x-2)(x+3)(5-x)<0\;\) jest \((-3,2)\cup(5,+\infty)\;\).
Zauważmy także, że zbiorem rozwiązań nierówności \((x-2)(x+3)(5-x)\leq0\;\) jest\break \(\langle-3,2\rangle\cup\langle5,+\infty\rangle\;\).
Zamiast tabeli można też użyć osi liczbowej z naniesionymi "ważnymi" punktami \(2,-3,5\;\) oraz znakami czynników w poszczególnych przedziałach.
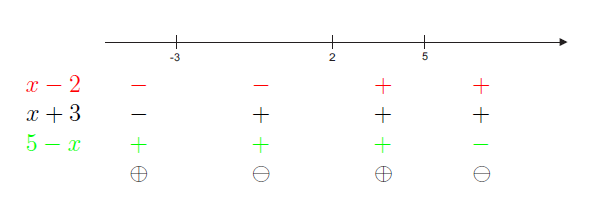
Znaki czerwone informują o znaku wyrażenia \(x-2\;\). Znaki czarne informują o znaku wyrażenia \(x+3\;\). Znaki zielone informują o znaku wyrażenia \(5-x\;\). Znaki iloczynu umieszczono "w kółkach". W oparciu o nie łatwo podać zbiór rozwiązań nierówności, np.
Zbiorem rozwiązań nierówności \((x-2)(x+3)(5-x)<0\;\) jest \((-3,2)\cup(5,+\infty)\;\).
Oznacza to, że pierwiastki wielomianu nanosimy na oś liczbową. Dokonany zostaje podział osi liczbowej na przedziały. W każdym z tych przedziałów ustalamy znak każdego czynnika występującego w rozkładzie wielomianu na czynniki. W każdym z tych przedziałów wartości wielomianu są stałego znaku.
Zadanie 7.2: Rozwiązać nierówność \((2x+3)(4-2x)(x-5)^2(x^2+1)<0\;\).
Rozwiązanie: Badamy znaki każdego z czynników oddzielnie w oparciu o znane własności funkcji liniowej i kwadratowej.
| \(2x+3\qquad\;\) | 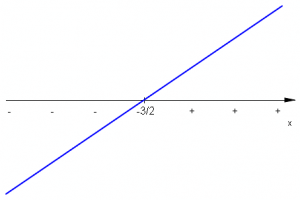 |
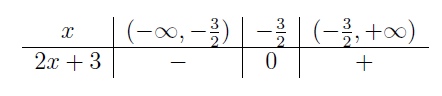 |
| \(4-2x\qquad\;\) | 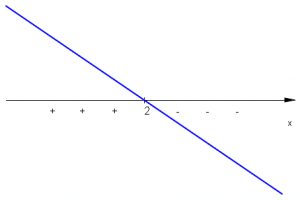 |
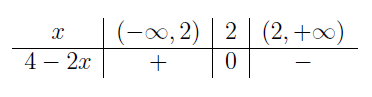 |
| \((x-5)^2\qquad\;\) | 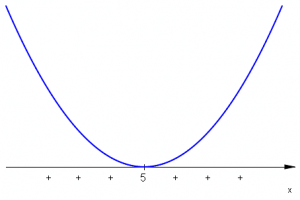 |
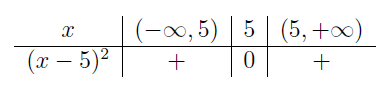 |
| \(x^2+1\qquad\;\) | 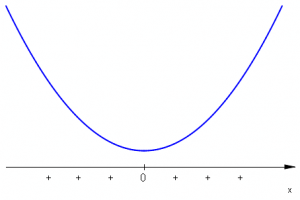 |
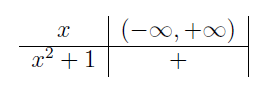 |
Ważnymi liczbami w naszych rozważaniach są \(-\frac{3}{2},2,5\;\). Zbieramy informacje w tabeli wypełniając kolejne wiersze, a następnie wyznaczając znak iloczynu \(W(x)=(2x+3)(4-2x)(x-5)^2(x^2+1)\;\).
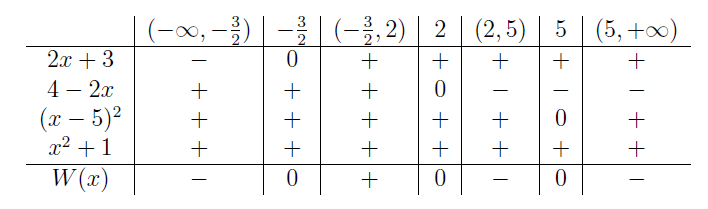
Z tabeli odczytujemy zbiór rozwiązań nierówności \(\left(-\infty,-\frac{3}{2}\right)\cup(2,5)\cup(5,+\infty)\;\).
Badanie znaku na osi liczbowej wyglądałoby w skrócie następująco
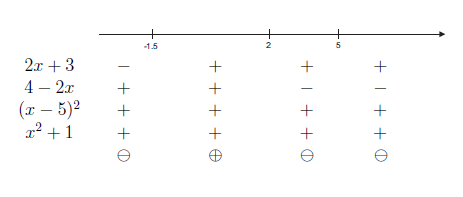
Znaki w kółkach oznaczają znaki wielomianu \(W(x)\;\) w poszczególnych przedziałach. Pozwalają na odczytanie zbioru rozwiązań nierówności \(\left(-\infty,-\frac{3}{2}\right)\cup(2,5)\cup(5,+\infty)\;\).
W przypadku nierówności \((2x+3)(4-2x)(x-5)^2(x^2+1)\leq 0\;\) otrzymujemy zbiór rozwiązań \((-\infty,-\frac{3}{2})\cup(2,+\infty)\;\).
Komentarz. Nasuwaja się dwie refleksje.
- "Ważne" przedziały dla zmiennej \(x\;\) wyznaczone są przez liczby będące rozwiązaniami równań powstałych przez przyrównanie do zera każdego z czynników. Równania
\( x+3=0,\quad 2-x,\quad x-1=0,\quad x^2+1=0 \;\)
wskazują ważne liczby: \(-3,2\;\) i \(1\;\). - Z uwagi na to, że wyrażenie \(x^2+1\;\) przyjmuje dla wszystkich liczb rzeczywistych \(x\;\) wartości dodatnie, można by na samym początku rozwiązywanie nierówności zastąpić badaną nierówność
\( (2x+3)(4-2x)(x-5)^2(x^2+1)<0 \;\)
nierównością równoważną
\( (2x+3)(4-2x)(x-5)^2<0. \;\)
Zauważmy, że nie można podobnie postąpić z czynnikiem \((x-5)^2\;\). Zbiorem rozwiązań nierówności \((2x+3)(4-2x)(x-5)^2<0\;\) jest bowiem zbiór \(\left(-\infty,-\frac{3}{2}\right)\cup(2,5)\cup(5,+\infty)\;\), podczas gdy zbiorem rozwiązań nierówności \((2x+3)(4-2x)<0\;\) jest \(\left(-\infty,-\frac{3}{2}\right)\cup(2,+\infty)\;\).
Obowiązuje
Reguła. Nierówność wielomianową można stronami podzielić przez wyrażenie algebraiczne wtedy, gdy dla wszystkich liczb rzeczywistych wartości zmiennej wyrażenie przyjmuje wartości dodatnie.
Metoda 2. (Wykres znaków)
Druga metoda rozwiązywania nierówności wielomianowych z wielomianem o postaci iloczynu czynników tylko liniowych lub kwadratowych z wyróżnikiem ujemnym jest szybka. U jej podstaw leży spostrzeżenie, że jeśli na osi zaznaczymy wszystkie pierwiastki \(x_1,x_2,\ldots,x_k\;\) wielomianu \(W(x)\;\), przy czym \(x_1<x_2<\ldots< x_k\;\), to dla liczb z ustalonego przedziału \((x_s,x_{s+1})\;\) o końcach będących kolejnymi pierwiastkami \(x_s\;\) i \(x_{s+1}\;\), wartości wielomianu \(W(x)\;\) sa stałego znaku. Na przykład, niech
\(
W(x) = (x+3)(x+1)x(4x-2)^2(x-4)^5(x^2+4).
\;\)
Pierwiastkami wielomianu \(W(x)\;\) są liczby \(-3, -1, 0, \frac{1}{2}, 4\;\). Jeśli \(t_1,t_2\in(-3,-1)\;\), to liczby \(W(t_1)\;\) i \(W(t_2)\;\) sa tego samego znaku; podobnie jeśli \(t_3,t_4\in(-\infty,-3)\;\), to liczby \(W(t_3)\;\) i \(W(t_4)\;\) sa tego samego znaku. Identyczna sytuacja ma miejsce, gdy rozważamy przedziały \(\left(0,\frac{1}{2}\right)\quad\;\), \(\left(\frac{1}{2},4\right)\qquad\;\), \((4+\infty)\;\).
Zademonstrujemy sposób tworzenia wykresu znaków wielomianu opisując rozwiązanie Zadania
Zadanie 7.3. Rozwiązać nierówność
\(
\left(x+\frac{3}{2}\right)(x+1)x(4x-2)^2(x-2)^5(x^2+4)<0.
\;\)
Rozwiązanie: Postępujemy według schematu.
1. Upewniamy się, czy w iloczynie występują tylko czynniki liniowe lub kwadratowe z wyróżnikiem ujemnym (iloczynów innego rodzaju tą metodą nie można analizować).
2. Każdy z czynników przyrównujemy do 0 i rozwiązania otrzymanych równań zaznaczamy na osi liczbowej.
Z równań \(x+\frac{3}{2}=0\;\); \(x+1=0\;\); \(x=0\;\); \(4x-2=0\;\); \(x-2=0\;\); \(x^2+4=0\;\) otrzymujemy rozwiązania \(-\frac{3}{2}, -1, 0, \frac{1}{2}, 2\;\).
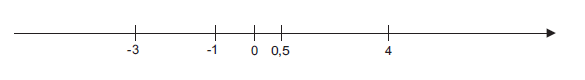
3. Sprawdzamy, jakiego znaku jest współczynnik przy najwyższej potędze zmiennej.
Wielomian \(W(x)\;\) jest stopnia \(1+1+1+2+5+2=12\;\) i przy \(x\;\) występuje współczynnik dodatni 16.
4. Rysujemy ciągłą linię według następujących reguł.
- linię zaczynamy rysować z prawego "końca" osi liczbowej; czyli "na prawo" od największego pierwiastka, przy czym
- zaczynamy linię znad osi, jeśli współczynnik ustalony w punkcie 3. jest dodatni
- zaczynamy linię spod osi, jeśli współczynnik ustalony w punkcie 3. jest ujemny
W naszym zadaniu współczynnik jest dodatni, więc linię zaczynamy rysować nad osią.
- prowadzimy linię od prawej do lewej strony docierając do kolejnych punktów osi wyznaczających pierwiastki wielomianu \(W(x)\;\), przy czym:
- jeśli krotność "odwiedzanego" przez nas pierwiastka jest nieparzysta, to linia przechodzi spod osi nad oś lub odwrotnie, przecinając oś,
- jeśli krotność "odwiedzanego" przez nas pierwiastka jest parzysta, to linia pozostaje w tej samej półpłaszczyźnie wyznaczanej przez oś.
Linia ta przekazuje informację o tym, jakie wartości, dodatnie, czy ujemne, ma ten wielomian w poszczególnych przedziałach. Linie tę nazywamy wykresem znaku wielomianu.
W naszym przypadku mamy:
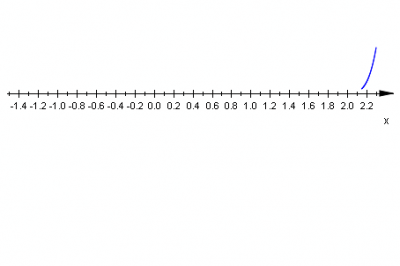 |
współczynnik przy \(x^{12}\;\) jest dodatni \(a_{12}=16\;\) |
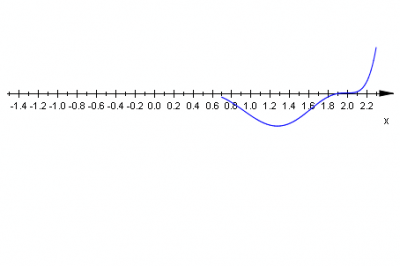 |
krotność pierwiastka \(x_1=2\;\) jest równa \(5\;\) |
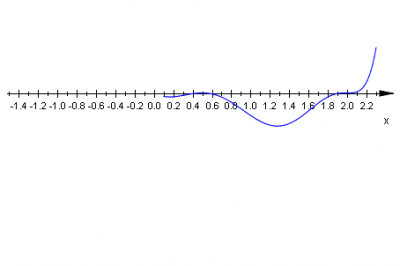 |
krotność pierwiastka \(x_2=\frac{1}{2}\;\) jest równa \(2\;\) |
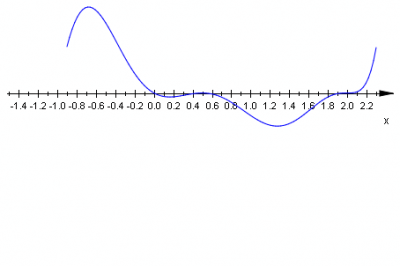 |
krotność pierwiastka \(x_3=0\;\) jest równa \(1\;\) |
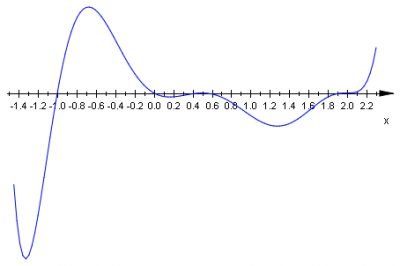 |
krotność pierwiastka \(x_4=-1\;\) jest równa \(1\;\) |
 |
krotność pierwiastka \(x_5=-\frac{3}{2}\;\) jest równa \(1\;\) |
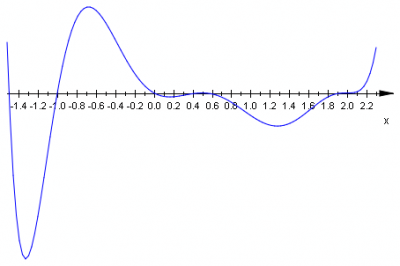
W ten sposób uzyskaliśmy wykres znaków wielomianu tzn.
- jeśli punkty linii znajdują się nad osią, wartości wielomianu dla liczb będących pierwszymi współrzędnymi tych punktów są dodatnie,
- jeśli punkty linii znajdują się pod osią, wartości wielomianu dla liczb będących pierwszymi współrzędnymi tych punktów są ujemne,
- punkty linii należące do osi liczbowej (tylko te, które zaznaczyliśmy na początku) wskazują pierwiastki wielomianu.
5. Odczytujemy zbiór rozwiązań nierówności z wykresu znaków.
Np. nierówność
\(
\left(x+\frac{3}{2}\right)(x+1)x(4x-2)^2(x-2)^5(x^2+4)<0
\;\)
jest prawdziwa dla \(x\in\left(-\frac{3}{2},-1\right)\cup\left(0,\frac{1}{2}\right)\cup\left(\frac{1}{2},2\right)\;\), a nierówność
\(
\left(x+\frac{3}{2}\right)(x+1)x(4x-2)^2(x-2)^5(x^2+4)\geq0
\;\)
jest prawdziwa dla \(x\in\left(-\infty,-\frac{3}{2}\right\rangle\cup\langle -1,0\rangle\cup\left\{\frac{1}{2}\right\}\cup\langle2,+\infty)\;\).
Zadanie 7.4. Rozwiązać nierówność
\(
(6x-5)(1-x)^3(4-3x)^2x^4(1-5x)^2\big((x+2)^2+1\big)(2x^2+x+6)^3\geq 0.
\;\)
Rozwiązanie: Szukamy "ważnych" punktów na osi liczbowej:
\(
6x-5=0;\quad 1-x=0;\quad 4-3x=0;\quad x=0;\quad 1-5x=0;\quad (x+2)^2+1=0;\quad 2x^2+x+6=0.
\;\)
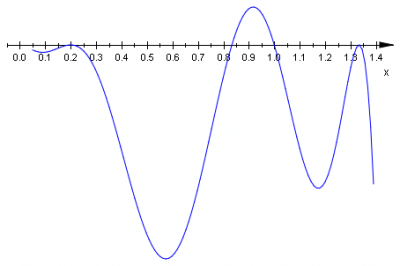
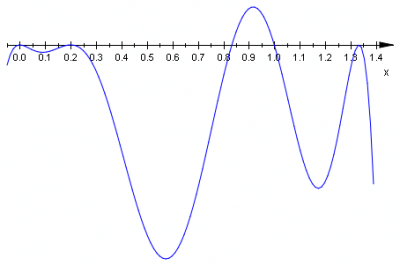
Z otrzymanych równań wyliczamy pierwiastki: \(\frac{5}{6}\;\), \(1\;\), \(\frac{4}{3}\;\), \(0\;\), \(\frac{1}{5}\;\). Rysujemy linię opisującą znaki wielomianu dla dowolnej liczby rzeczywistej, zauważmy, że stopień wielomianu jest równy \(1+3+2+4+2+2+2\cdot 3=20\;\).
 |
współczynnik przy \(x^{20}\;\) jest ujemny \(a_{20}=6\cdot(-1)^3\cdot(-3)^2\cdot 1^4\cdot (-5)^2\cdot 1\cdot 2^3<0\;\) |
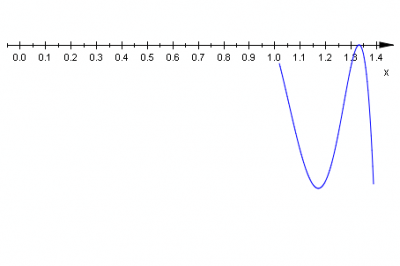 |
krotność \(x_1=\frac{4}{3}\;\) jest równa \(2\;\) |
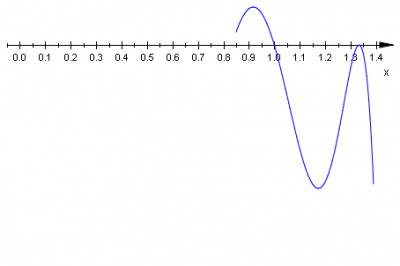 |
krotność \(x_2=1\;\) jest równa \(3\;\) |
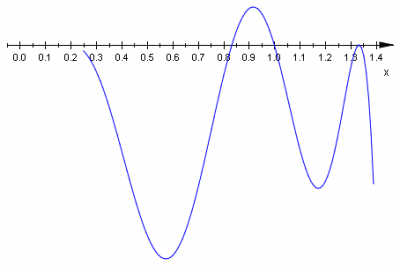 |
krotność \(x_3=\frac{5}{6}\;\) jest równa \(1\;\) |
 |
krotność \(x_4=\frac{1}{5}\;\) jest równa \(2\;\) |
 |
krotność \(x_5=0\;\) jest równa \(4\;\) |
Z wykresu odczytujemy zbiór rozwiązań nierówności \(W(x)\geq 0\;\): \(\left\{0,\frac{1}{5},\frac{4}{3}\right\}\cup\left\langle\frac{5}{6},1\right\rangle\;\).
Uwaga 7.1. Metoda 1. i Metoda 2. pozwalały na rozwiązanie nierówności wielomianowej tylko w przypadku postaci \(W(x)>0\;\) (\(W(x)\geq 0\;\), \(W(x)< 0\;\), \(W(x)\leq 0\;\)), gdzie \(W(x)\;\) jest iloczynem czynników liniowych lub kwadratowych z wyróżnikiem ujemnym. W każdym innym przypadku należy nierówność sprowadzić do tej właśnie postaci. Przykłady takich sytuacji demonstrujemy w kolejnych dwóch zadaniach. ∎
Zadanie 7.5. Rozwiązać nierówność \((x^2-x)(3x^2-2)\leq 5(x^3-x^2)\;\).
Zadanie 7.6. Rozwiązać nierówność \((x^8-81)(-x^2+4x-3)(9-x^2)^3\leq 0\;\).
Uwaga 7.2. Metoda 1. rozwiązywania nierówności wielomianowych wynika z własności funkcji liniowej, funkcji kwadratowej oraz własności mnożenia liczb oraz wyrażeń algebraicznych. Zastosowanie Metody 2. polega na wykonaniu serii określonych czynności według ustalonych reguł. Nasuwa się pytanie, dlaczego stosujemy właśnie takie reguły. W opisie Metody 2. wspomniano już, że jej podstawą jest fakt, iż między "sąsiednimi" pierwiastkami wielomianu przyjmuje on wartości stałego znaku. Ale powstają pytania:
- skąd bierze się reguła: "gdy współczynnik przy najwyższej potędze zmiennej jest dodatni, to rysowanie linii zaczynamy nad osią" itd.,
- dlaczego przy nieparzystych krotnościach pierwiastka linia przecina oś, a przy parzystych --- linia pozostaje po tej samej stronie osi.
Odpowiedź na pierwsze pytanie wiąże sie z pewną własnością wielomianów, którą wytłumaczymy na przykładzie.
Niech \(W(x)=3x^3+100x^2-150x-3000\;\). Wówczas dla \(x\ne 0\;\) mamy
\(
W(x) = x^3\left(3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\right).
\;\)
Gdy rozważamy liczby \(x\;\) większe niż np. 1000, to
\(
3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}>3-\frac{150}{1000^2}-\frac{3000}{1000^3}>3-\frac{2}{10}>2
\;\)
i dlatego
\(
W(x) = x^3\left(3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\right)>x^2\cdot 2,\!8>0.
\;\)
Zatem dla "dużych" liczb \(x\;\) (np. dla \(x>1000\;\)) wielomian \(W(x)\;\) przyjmuje wartości dodatnie. Liczba \(3\;\) "zdominowała" wszystkie pozostałe składniki sumy \(3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\;\) dla "dużych" liczb dodatnich. Wykres znaków rozpoczynamy "z prawej strony osi, znad osi".
Niech \(P(x)=-3x^3+100x^2-150x-3000\;\). Wówczas dla \(x\ne 0\;\) mamy
\(
P(x) = x^3\left(-3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\right).
\;\)
Gdy rozważamy liczby \(x\;\) większe niż np. 1000, to
\(
-3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}<-3+\frac{100}{1000}<-2
\;\)
i dlatego
\(
P(x) = x^3\left(-3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\right)<-2x^3<0.
\;\)
Zatem dla "dużych" liczb \(x\;\) (np. dla \(x>1000\;\)) wielomian \(P(x)\;\) przyjmuje wartości dodatnie. Liczba \(-3\;\) "zdominowała" wszystkie pozostałe składniki sumy \(-3+\frac{100}{x}-\frac{150}{x^2}-\frac{3000}{x^3}\;\) dla "dużych" liczb dodatnich. Wykres znaków rozpoczynamy "z prawej strony osi, spod osi".
Podobnie można wytłumaczyć własności dowolnego wielomianu stopnia \(k\;\), \(W(x)=a_kx^k+a_{k-1}x^{k-1}+\ldots+a_1x+a_0\;\), \(a_k\ne 0\;\).
Jeśli \(a_k>0\;\), to dla "dużych" liczb \(x\;\)
\(
W(x) = x^k\left(a_k+\frac{a_{k-1}}{x}+\frac{a_{k-2}}{x^2}+\cdots+\frac{a_0}{x^k}\right)>0,
\;\)
jeśli zaś \(a_k<0\;\), to dla "dużych" liczb \(x\;\)
\(
W(x) = x^k\left(a_k+\frac{a_{k-1}}{x}+\frac{a_{k-2}}{x^2}+\cdots+\frac{a_0}{x^k}\right)<0.
\;\)
Odpowiedź na drugie pytanie wynika z następującego spostrzeżenia.
Niech \(c\;\) będzie dowolną liczbą rzeczywistą i \(k\;\) dowolną liczbą całkowitą dodatnią.
- Jeśli \(k\;\) jest nieparzysta, to
- \((x-c)^k<0\;\) dla liczb mniejszych niż \(c\;\),
- \((x-c)^k>0\;\) dla liczb większych niż \(c\;\).
- Jeśli \(k\;\) jest parzysta, to \((x-c)^k>0\;\) dla wszystkich liczb \(x\ne c\;\).
Dlatego, gdy badamy znak iloczynu, w którym występuje czynnik \((x-c)^k\;\), to obserwujemy
- różne znaki tego iloczynu dla liczb \(x\;\) "znajdujących się w pobliżu" liczby \(c\;\) "z lewej jej strony" i "z prawej jej strony", gdy liczba \(k\;\) jest nieparzysta;
- stały znak tego iloczynu dla liczb \(x\;\) "znajdujących się w pobliżu" liczby \(c\;\), zarówno "z lewej jej strony" jak i "z prawej jej strony", gdy liczba \(k\;\) jest parzysta;
