Iteracja I

Iteracja [łac. iteratio "powtórzenie"], w matematyce wielokrotne powtarzanie tych samych operacji (np. działań arytmetycznych, przekształceń) na obiektach matematycznych lub danych przetwarzanych za pomocą programów komputerowych; wykorzystywana m.in. w metodach numerycznych; jedno z podstawowych pojęć informatyki. [Encyklopedia PWN]

Zadanie spirala

W prostokątnym układzie współrzędnych dane są dwa punkty, na których rozpięto prostokąt o bokach równoległych do osi. Ze środka układu rysujemy łamaną o kształcie spirali: z wierzchołka (0,0) prowadzimy odcinek o długości 1 na północ (zgodnie z kierunkiem i zwrotem wektora [0,1]), następnie odcinek o długości 2 na wschód (zgodnie z kierunkiem i zwrotem wektora [1,0]), następnie o długości 4 na południe (kierunek i zwrot wektora [0,-1]), następnie o długości 8 na zachód (kierunek i zwrot wektora [-1,0]), potem o długości 16 znów na północ itd., za każdym razem podwajając długość odcinka i zmieniając kierunki zgodnie z ruchem wskazówek zegara. Należy znaleźć pierwszy wierzchołek spirali, który leży poza prostokątem (tzn. poza jego wnętrzem i poza brzegiem).

Dane: prostokąt o bokach równoległych do osi, zadany przez dwa przeciwległe punkty w prostokątnym układzie współrzędnych.

Wynik: współrzędne pierwszego wierzchołka spirali leżącego poza prostokątem.

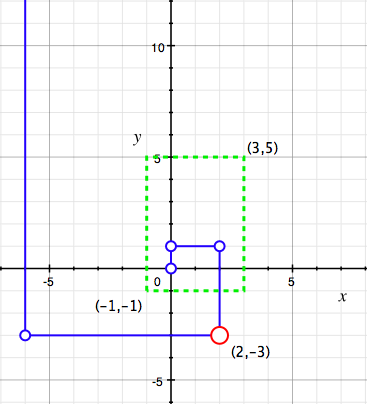
Oto sformalizowana metoda wyznaczania kolejnych wierzchołków spirali:

weź wektor [0,1] (północ)
weź długość odcinka 1
weź punkt (0,0)
powtarzaj
  narysuj wierzchołek w bieżącym punkcie
  przesuń punkt zgodnie z wektorem i długością odcinka
  podwój długość odcinka
  obróć wektor o kąt prosty w prawo

Niewiele potrzeba, by przerobić ją na algorytm znajdowania pierwszego wierzchołka leżącego poza prostokątem:

weź wektor kierunku [0,1] (północ)
weź długość odcinka 1
weź punkt (0,0)
dopóki punkt leży na prostokącie
  przesuń punkt zgodnie z wektorem i długością odcinka
  podwój długość odcinka
  obróć wektor o kąt prosty w prawo
bieżący punkt jest pierwszym wierzchołkiem poza prostokątem

Oto implementacja powyższego algorytmu. Potrzebujemy dwóch funkcji pomocniczych:

def naProstokącie(x,y, w1x, w1y, w2x, w2y):
    return ( min(w1x,w2x) <= x <= max(w1x,w2x)
          and min(w1y,w2y) <= y <= max(w1y,w2y) )
 
def obrocWPrawo(vx, vy):
    return (vy, -vx)
 
def pierwszyWierzchLamanejPozaProstokatem(w1x, w1y, w2x, w2y):
    x,y = (0,0)
    kierx,kiery = (0,1)
    dlugosc = 1
 
    while naProstokacie( x,y, w1x, w1y, w2x, w2y ):
        x = x + kierunekx * dlugosc
        y = y + kieruneky * dlugosc
        kierunekx, kieruneky = obrocWPrawo(kierunekx, kieruneky)
        dlugosc = dlugosc * 2
 
    return (x,y)

Oto przykładowy ślad wykonania głównej funkcji z programu dla spirali:

pierwszyWierzchLamanejPozaProstokatem(-1, -1, 3, 5):

    x,y = (0, 0)
    kierx, kiery = (0, 1)
    dlugosc = 1

    sprawdzenie dozoru: naProstokącie(0, 0,  -1, -1,  3, 5) → prawda
    x = 0 + 0 * 1                     czyli 0
    y = 0 + 1 * 1                     czyli 1
    kierx, kiery = obrocWPrawo(0, 1)  czyli (1, 0)
    dlugosc = 2 * 1                   czyli 2

    sprawdzenie dozoru: naProstokacie(0, 1,  -1, -1,  3, 5) → prawda
    x = 0 + 1 * 2                     czyli 2
    y = 1 + 0 * 2                     czyli 1
    kierx, kiery = obrocWPrawo(1, 0)  czyli (0, -1)
    dlugosc = 2 * 2                   czyli 4

    sprawdzenie dozoru: naProstokacie(2, 1,  -1, -1,  3, 5) → prawda
    x = 2 + 0 * 4                     czyli 2
    y = 1 + (-1) * 4                  czyli -3
    kierx, kiery = obrocWPrawo(1, 0)  czyli (-1, 0)
    dlugosc = 4 * 2                   czyli 8

    sprawdzenie dozoru: naProstokacie(2, -3,  -1, -1,  3, 5) → fałsz

    return (2, -3)

W opisanym algorytmie korzystamy z gwarancji pętli while: wykonanie pętli kończy się przy pierwszym niespełnieniu dozoru. Tutaj, po znalezieniu pierwszego wierzchołka łamanej nie leżącego na prostokącie.

Anatomia pętli while

Pętla while składa się z warunku (tzw. dozoru) oraz instrukcji (jednej lub wielu). Wykonanie pętli while to ciąg sprawdzeń, czy dozór jest spełniony; jeżeli tak, to wykonywane są instrukcje, po czym znowu sprawdzany jest dozór, jeśli jest spełniony, to ponownie wykonywane są instrukcje itd., aż do momentu, kiedy dozór po raz pierwszy okaże się niespełniony.

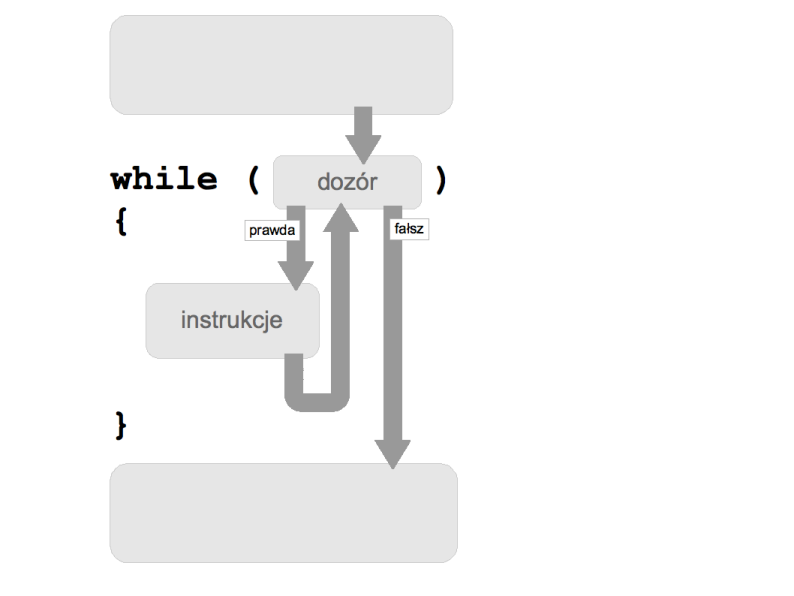
Pętla while daje programiście dwie gwarancje:

1. wykonanie instrukcji pętli rozpoczyna się tylko przy spełnionym dozorze;
2. wykonanie pętli kończy się przy pierwszym niespełnieniu dozoru.

W algorytmie z zadania Spirala korzystamy z tej drugiej gwarancji. Dozór pętli mówi wierzchołek spirali wciąż znajduje się w dozwolonych granicach.
Zakończenie pętli oznacza znalezienie pierwszego momentu, w którym ten warunek został złamany.

Zadanie pierwiastek dyskretny

Pierwiastkiem dyskretnym z liczby naturalnej \(n\) nazywamy największą liczbę naturalną, której kwadrat nie przekracza \(n\). Innymi słowy, jest to największa liczba naturalna \(p\) spełniająca nierówność \(p^2 \le n\). Napisz program znajdujący pierwiastek dyskretny i korzystający wyłącznie z dodawania i mnożenia (bez potęgowania).

Dane: liczba naturalna n.

Wynik: pierwiastek dyskretny z n.

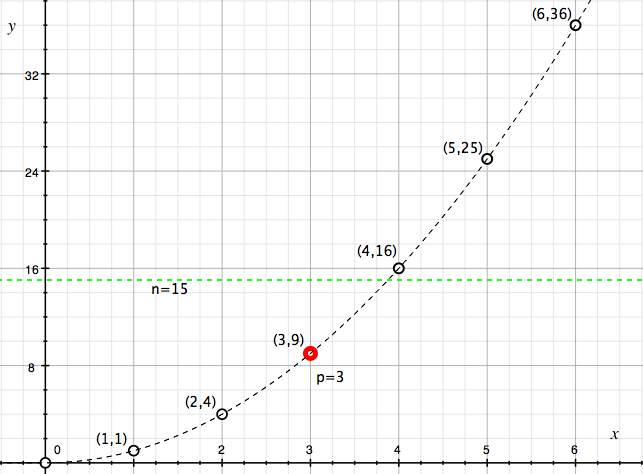
Spójrzmy na wykres funkcji \(f(x)=x^2\) dla liczb naturalnych. Będziemy się przyglądali liczbom spełniającym nierówność pierwiastka \(x^2\le n\), więc rysujemy kreskę na poziomie liczby \(n\). W pewnym momencie punkty wykresy przekraczają poziom \(n\), a współrzędna \(x\) ostatniego punktu nie wystającego ponad kreskę jest poszukiwaną liczbą \(p\) (bo jest największym naturalnym rozwiązaniem nierówności pierwiastka). Widać także, że wszystkie wartości funkcji dla argumentów od następnika \(p\) począwszy nie spełniają nierówności pierwiastka.

Łatwo wymyślić algorytm, który przegląda kolejnych kandydatów na pierwiastek, zatrzymując się, gdy po raz pierwszy następnik kandydata nie spełnia nierówności pierwiastka.

weź 0 na kandydata
dopóki następnik kandydata spełnia nierówność pierwiastka:
  niech ten następnik będzie nowym kandydatem
aktualny kandydat to poszukiwany pierwiastek dyskretny

def pierwiastekDyskretny(n):
    k = 0
    while (k+1)*(k+1) <= n:
        k = k + 1
    return k 

Przypomnijmy, pętla while daje programiście dwie gwarancje:

1. wykonanie instrukcji pętli rozpoczyna się tylko przy spełnionym dozorze;
2. wykonanie pętli kończy się przy pierwszym niespełnieniu dozoru.

Z gwarancji (1) korzystamy wewnątrz pętli - skoro następnik kandydata spełnia nierówność pierwiastka, to kandydat nie może być tym poszukiwanym największym, będziemy więc próbować szczęścia z jego następnikiem. Na podstawie gwarancji (2) wiemy, że po zakończeniu pętli następnik kandydata nie spełnia nierówności pierwiastka. Skąd jednak wiadomo, że po zakończeniu pętli kandydat spełnia nierówność pierwiastka? Ten warunek jest spełniony na wstępie (zero spełnia nierówność pierwiastka \(0^2\le n\)), a pętla jest zbudowana w ten sposób, żeby nie popsuć tego warunku.

def pierwiastekDyskretny(n):
    k = 0
        # <- kandydat k (==0) spełnia nierówność pierwiastka
    while (k+1)*(k+1) <= n:
            # <- kandydat k spełnia nierówność pierwiastka,
            #    a na podstawie zachodzenia dozoru wiemy, że również
            #    następnik k spełnia nierówność pierwiastka
        k = k+1
            # <- zmieniła się wartość k,
            #     następnik stał się nowym kandydatem,
            #     tym niemniej wciąż
            #    kandydat k spełnia nierówność pierwiastka
    return k
    # <- kandydat k spełnia nierówność pierwiastka,
    #    a z nie zachodzenia dozoru wiemy, że
    #    następnik k nie spełnia nierówności pierwiastka,
    #    zatem kandydat k jest pierwiastkiem dyskretnym z n

Warunek logiczny przypisany do konkretnego miejsca w kodzie programu lub opisie algorytmu nazywamy asercją. Asercję, która jest zawsze prawdziwa, nazywamy niezmiennikiem. Asercję, która jest zawsze prawdziwa w momencie sprawdzania dozoru pętli nazywamy niezmiennikiem pętli.

Własność stopu

Oto ślad przykładowego obliczenia:

  pierwiastekDyskretny(15):

    k = 0

    sprawdzenie dozoru: (0+1)*(0+1) <= 15  → prawda
      k = 0 + 1                            
    
    sprawdzenie dozoru: (1+1)*(1+1) <= 15  → prawda
      k = 1 + 1                            

    sprawdzenie dozoru: (2+1)*(2+1) <= 15  → prawda
      k = 2 + 1                            
    
    sprawdzenie dozoru: (3+1)*(3+1) <= 15  → fałsz

    return 3

Powyższy ślad kończy się po trzech obrotach pętli. Ale obliczenie nie zawsze musi być skończone, np. taka pętla

while x != 0:
   x = x - 1;

zakończy działanie lub nie, w zależności od początkowej wartości zmiennej \(x\). Jeżeli \(x\) będzie przebiegać liczby całkowite, przy tym na początku wykonania programu będzie liczbą nieujemną, to prędzej czy później kolejne przebiegi pętli sprowadzą \(x\) do zera, a wówczas niespełnienie dozoru spowoduje zakończenie wykonania pętli. W pozostałych przypadkach widzimy, że startując z \(x\) o wartości niecałkowitej dodatniej "miniemy" zero, natomiast startując od liczby ujemnej w ogóle się do niego nie zbliżymy.

Funkcja pierwiastekDyskretny zachowuje się lepiej. Wyrażenie \((k+1)*(k+1)\) stojące po lewej stronie nierówności w dozorze pętli przyjmuje wartości naturalne, które rosną z każdym obrotem pętli; mamy więc pewność, że prędzej czy później wartość wyrażenia przekroczy zadaną wartość \(n\), skutkiem czego wykonywanie pętli się zakończy.

O algorytmie lub programie, którego wykonywanie kończy się dla dowolnych danych wejściowych spełniających specyfikację zadnia, mówimy że ma własność stopu. Uzasadnianie własności stopu, jest jednym z najtrudniejszych elementów projektowania pętli.

ZADANIA

Zadanie 1

W programach komputerowych, tak jak w notacji matematycznej, różne działania mają różne priorytety: np. mnożenie (*) i dzielenie (/) mają pierwszeństwo przed dodawaniem (+) i odejmowaniem (-). By wymusić nietypową kolejność wykonywania działań lub by rozwiać wątpliwości można stosować nawiasy. Np. wyrażenie a + b * c można ponawiasować (a + b) * c lub a + (b * c). Ten drugi sposób odpowiada naturalnej kolejności obliczania wyrażanie a + b * c, natomiast pierwszy sposób wymusza wykonanie dodawania przed mnożeniem.

Przyjmijmy, że a==6, b==8, c==2, d==0.
Podaj uściślające nawiasowania lub narysuj drzewa obliczenia dla następujących wyrażeń.

• Wyrażenie a + b / c + d ma wartość 10. Wstaw nawiasy tak, by miało wartość 7. Odpowiedź: (a + b) / c + d == 7.
• Wyrażenie a - b - c ma wartość -4. Wstaw nawisy tak, by miało wartość 0. Odpowiedź: a - (b - c) == 0.
• Wyrażenie a - b * c ma wartość -10. Wstaw nawiasy tak, by miało wartość -4. Odpowiedź: (a - b) * c == -4.

Przyjmijmy, że x==True, y==True, z==False. W języku programowania Python operatorami logicznymi i oraz lub są odpowiednio and i or.

• Wyrażenie logiczne x and y or z ma wartość False. Wstaw nawiasy tak, by miało wartoćć True. Odpowiedź: nie jest to możliwe, wyrażenie zawsze będzie miało wartość False, niezależnie od nawiasowania
• Wyrażenie x or y and z ma wartość True. Wstaw nawiasy tak, by miało wartość False. Odpowiedź: (x or y) and z.

Zadanie 2

W matematyce występują oznaczenia na przedziały liczb rzeczywistych, np. \(\langle a;b)\) lub \([a,b)\). W matematycznych opisach programów przydają się podobne oznaczenia na przedziały liczb całkowitych (Z oznacza zbiór wszystkich liczb całkowitych):

\([a..b] = \{ x \in Z : a \leq x \leq b \}\)

\([a..b) = \{ x \in Z : a \leq x < b \}\)

\((a..b] = \{ x \in Z : a < x \leq b \}\)

\((a..b) = \{ x \in Z : a < x < b \}\)

Wartości \(a\) i \(b\) są liczbami całkowitymi takimi, że \(a\leq b\). Ile jest elementów w przedziale:

• \([0..5)\) Odpowiedź: 5 (\([0..5) = \{0,1,2,3,4\}\)).
• \([2..3)\) Odpowiedź: jeden.
• \([3..1)\) Odpowiedź: zero.
• \([0..a)\) Odpowiedź: \(a\), gdy \(a\) jest nieujemne i 0 w przeciwnym przypadku.
• \([a..b]\) Odpowiedź: \(b - a + 1\).
• \([a..b)\) Odpowiedź: \(b - a\).
• \((a..b]\) Odpowiedź: \(b - a\).
• \((a..b)\) Odpowiedź: \(b - a - 1\), ale oczywiście nie mniej niż 0. Możemy to zapisać tak: \(max(0, b - a - 1)\)
• \([0..b)\) Odpowiedź: \(b\), jeśli \(b\) nieujemne; 0 w przeciwnym przypadku. (Innymi słowy, \(max(0,b)\)).
• \([a..2*a)\) Odpowiedź: \(max(0,a)\).
• \([-a..a]\) Odpowiedź: \(max(0,2*a+1)\) (\(a\) elementów ujemnych, \(a\) elementów dodatnich, zero; stąd \(2*a+1\)).

Zadanie 3

Zapisz w zwięzłej formie zbiór tych wartości, dla których zostanie wywołana funkcja f w poniższych programach (o ile to możliwe posłuż się notacją dla przedziałów całkowitoliczbowych z zadania 2). Oblicz liczność (tj. liczbę elementów) każdego z tych zbiorów.

k = 0
while k < q:
    f(k)
    k = k + 1

Odpowiedź:

\([0..q)\), \(max(0,q)\) elementów.

k = 1
while k <= q:
    f(k)
    k = k + 1

Odpowiedź:

\([1..q]\), \(max(0,q)\) elementów.

k = 0
while k <= q:
    f(k)
    k = k + 1

Odpowiedź:

\([0..q]\), \(max(0,q+1)\) elementów.

k = p
while k < q:
    f(k)
    k = k + 1

Odpowiedź:

\([p,q)\), \(max(0,q-p)\) elementów.

k = p
while k < q:
    k = k + 1
    f(k)

Odpowiedź:

\([p+1,q+1)\), \(max(0,q-p)\) elementów

k = p
while True:
    f(k)
    k = k + 1
    if k >= q: break

Odpowiedź:

\(\{p\}\cup (p, q)\), \(1 + max(0,q-p-1)\) elementów

k = p
while k > 0:
    k = k - 1
    f(k)

Odpowiedź:

\([0..p)\), \(max(0,p)\) elementów.

**

k = p
while k != 1:
    f(k)
    if parzysta(k): k = k / 2
    else: k = 3 * k + 1

Rozwiązanie:

Jeśli udało Ci się rozwiązać ten podpunkt, to szczerze gratulujemy! W roku 1937 Lothar Collatz zadał pytanie, czy dla dowolnej liczby naturalnej \(p\) wykonanie tego programu się kończy (innymi słowy, czy liczba wywołań funkcji \(f\) jest skończona). Odpowiedzi do tej pory nie znaleziono. Program Collatza w języku Pascal umieszczono jako ozdobę na elewacji Biblioteki Uniwersytetu Warszawskiego.

ZADANIE 4

Uzupełnij poniższy program:

k = ...
while ...:
    ...
    f(k)
    ...

w ten sposób, by funkcja f została wywołana

• kolejno dla liczb \(0, 1, ..., n-1\),
• kolejno dla liczb \(n-1, n-2, ..., 0\),
• kolejno dla liczb \(1, ..., n\),
• kolejno dla liczb \(n, ..., 1\),
• po razie dla wszystkich liczb parzystych z przedziału \([p..q)\),
• po razie dla wszystkich liczb całkowitych, których kwadraty znajdują się w przedziale \([p..q)\).

Zadanie 5

Co się stanie, gdy wywołamy pierwiastekDyskretny(0) ?

Zadanie 6

W matematyce największą liczbę całkowitą nie przekraczającą liczby rzeczywistej \(x\) oznaczamy przez \(\lfloor x \rfloor\) lub \([x]\), a czasem \(E(x)\), albo też \(Ent(x)\). Tę liczbę nazywamy podłogą z x, częścią całkowitą x lub entier z x. Na przykład, gdy \(x=\pi=3.1415...\) różnymi liczbami całkowitymi nie przekraczającymi x są -10000, -7, 1, 3 i wiele innych. Największą z tych liczb jest 3, więc \(\lfloor\pi\rfloor = 3\). Analogicznie definiujemy sufit \(\lceil x\rceil\), jako najmniejszą liczbę całkowitą nie mniejszą niż \(x\). Przykłady:

Uzasadnij, że

• \(\lfloor x\rfloor \le x \le \lceil x\rceil\),
• \(\lfloor x\rfloor = \lceil x\rceil\) wtedy i tylko wtedy, gdy \(x\) jest liczbą całkowitą,
• pierwiastek dyskretny z \(n\) równa się \(\lfloor\sqrt{n}\rfloor \).

Zadanie 7

Niech \(p \ge 2, n \ge 1\) będą liczbami całkowitymi. Logarytmem dyskretnym przy podstawie \(p\) z liczby \(n\) nazywamy największą (nieujemną) liczbę całkowitą \(k\) taką, że \(p^k \le n\). Pamiętajmy przy tym, że \(p^0 == 1\).

Napisz funkcję, która dla danych liczb całkowitych \(p \ge 2, n \ge 1\) obliczy logarytm dyskretny przy podstawie \(p\) z \(n\). W swoim rozwiązaniu możesz posługiwać się tylko operacjami dodawania i mnożenia dla liczb całkowitych. Podaj niezmiennik pętli.

Wskazówka:

Logarytmem dyskretnym z \(n\) przy podstawie \(p\) nazywamy liczbę całkowitą \(k\) taką,że \(p^k \le n\) i jednocześnie \(p^{k+1} > n\).

Zadanie 8

Mamy sznur i wstążkę. Na ile sznurków o długości wstążki można pociąć dany sznur? Zapisz algorytm obliczający odpowiedź. Do dyspozycji masz tylko sznur, wstążkę, ręce i liczydło.

Rozwiązanie:

Oto jeden z możliwych sposobów:

  niech liczydło wskazuje 0
  ułóż sznur na stole
  przyłóż początek wstążki do początku sznura
  dopóki wstążka ułożona wdłuż sznura nie sięga poza jego koniec,
      zwiększ wartość na liczydle o jeden
      przesuń początek wstążki do punktu sznura, gdzie sięga jej koniec
  zwróć wartość wskazywaną przez liczydło

Zadanie 9

Dane są dwie liczby całkowite \(s \ge 0\) oraz \( w > 0 \).
Napisz funkcję obliczającą, ile razy liczba \(w\) mieści się (całkowicie) w liczbie \(s\).
Na przykład liczba w=3 w liczbie s=7 mieści się całkowicie 2 razy.
Innymi słowy, napisz program obliczający liczbę k taką, że zachodzi równość

s = k * w + r

dla pewnej liczby r z przedziału [0..k). Na przykład dla s=7 i w=3

7 = 2 * 3 + 1

Program powinien korzystać tylko z dodawania i odejmowania. Podaj niezmiennik pętli.

Wskazówka:

Skorzystaj z rozwiązania zadania 8.

Rozwiązanie:

Do rozwiązania tego zadania można wykorzystać algorytm podziału sznura z zadania 8. Przykładanie wstążki do kolejnych odcinków sznura to nic innego jak odejmowanie liczby \(w\) od \(s\). Wynikiem takiego obliczenia jest iloraz całkowity \(s//w\).

def ilorazCalkowity(s, w):
    k = 0
    reszta = s    # "niezużyta część sznura"
    while w <= reszta:
        k = k+1
        reszta = reszta-w
    return k

Zadanie 10

Dane są dwie liczby całkowite \(s \ge 0\) oraz \( w > 0 \).
Napisz program obliczający resztę z dzielenia liczby \(w\) przez liczbę \(s\).
Na przykład liczba w=3 podzielona przez s=7 daje resztę 1.
Dopuszczalne operacje: porównania, dodawanie, odejmowanie.

Wskazówka:

Wystarczy wziąć rozwiązanie zadania 9 i dokonać następujących zmian:

• zmienić nazwę funkcji z "ilorazCałkowity" na "resztaDzielenia"
• zmienić "return k" na "return reszta"

Mając też iloraz całkowity można resztę z dzielenia policzyć następująco:

def resztaDzielenia(s, w):
    return s - ilorazCalkowity(s, w)*w

Wykorzystując operator dzielenia całkowitego // (w Pythonie) można to zapisać tak:

def resztaDzielenia(s, w):
    return s - (s // w)*w

Zadanie 11

Napisz funkcję "parzysta" o jednym argumencie będącym liczbą całkowitą. Funkcja powinna zwracać wartość logiczną (prawda/fałsz) określającą parzystość argumentu funkcji.

Wskazówka:
Skorzystaj z operacji obliczania reszty z dzielenia.

Rozwiązanie:

def parzysta(k):
    return resztaDzielenia(k, 2) == 0

def parzysta(k):
    return k % 2 == 0

gdzie % jest operatorem modulo - brania reszty z dzielenia.

Zadanie 12

Uzasadnij, że program podany w rozwiązaniu zadania 9 faktycznie oblicza iloraz całkowity.

Rozwiązanie:

Przypomnijmy algorytm obliczania ilorazu całkowitego \(s//w\) z zadania 8 ( \(s\geq 0, w>0\) ):

    niech k = 0
    niech reszta = s
    dopóki w <= reszta:
        zwiększ k o jeden
        zmniejsz resztę o w
    zwróć k

Sztuka polega na znalezieniu odpowiednich niezmienników pętli. Niezmiennik to dowolne zdanie logiczne, które jest prawdziwe każdorazowo przed obliczeniem dozoru pętli.

Zauważmy, że operacja wykonywana w pętli, to jakby przekładanie odcinków o długości \(w\) z \(reszty\) do \(k\). To co zabierzemy z \(reszty\), odznaczamy w \(k\). Przed każdym obrotem pętli zachodzi warunek:

s = k * w + reszta

Początkowo

s = 0 * w + s

natomiast po zakończeniu pętli wartość \(reszta\) jest wyczerpana, nie da się z niej wyjąć już żadnego \(w\) bez czynienia jej ujemną (wynika to z dozoru pętli; po zakończeniu pętli prawdziwa jest negacja dozoru, czyli \(w > reszta\)). Ponadto, warunek pętli jest tak skonstruowany, że zachodzi jeszcze jeden niezmiennik:

reszta >= 0

To zdanie faktycznie jest niezmiennikiem, bo (a) na początku \(reszta=s\) (a z założenia \(s \geq 0\)), (b) warunek \(reszta \geq 0\) może się popsuć tylko podczas zmniejszania \(reszty\) o \(w\), ale pętla jest skonstruowana tak, że ta operacja zachodzi wyłącznie pod warunkiem "w <= reszta".

Po zakończeniu pętli zachodzą zatem następujące warunki:

s = k * w + reszta (niezmiennik)
reszta >= 0 (niezmiennik)
w < reszta (negacja dozoru)

czyli

s = k * w + reszta
0 <= reszta < w

a to jest dokładnie definicja ilorazu całkowitego (zob. treść zadania 8).

Zadanie 13

Liczba lustrzana S do danej liczby naturalnej Z to taka, która w zapisie dziesiętnym ma te same cyfry, tylko w odwrotnej kolejności, np. Z=123, S=321. Napisz funkcję "lustrzana", która oblicza liczbę lustrzaną argumentu. Dopuszczalne operacje: porównania, mnożenie, dodawanie, reszta z dzielenia, dzielenie całkowite.

Rozwiązanie

Po pierwsze, musimy w jakiś sposób arytmetycznie "rozłożyć" wartość liczby na poszczególne cyfry. W zasadzie wystarczy, jeśli za pomocą operacji arytmetycznych uda nam się "oddzielić" ostatnią cyfrę, a daje się to zrobić za pomocą dzielenia z resztą przez 10:

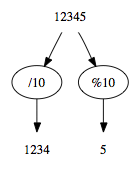
W analogiczny sposób możemy "dokleić" ostatnią cyfrę za pomocą mnożenia i dodawania:

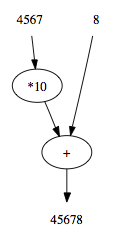
Algorytm konstrukcji liczby lustrzanej dla Z == 12345, oparty na oddzielaniu i doklejaniu ostatniej cyfry mógłby działać tak:

          p                 q
          12345             .
          1234              5
          123              54
          12              543
          1              5432
          .             54321=S

Kiedy czytamy cyfry liczby p, a następnie cyfry liczby q wspak, to zawsze otrzymujemy wyjściową liczbę Z. Kiedy natomiast czytamy cyfry liczby q, a następnie cyfry liczby p wspak, to zawsze otrzymujemy szukaną liczbę lustrzaną S. Ten warunek zachodzi w każdym wierszu tabelki. Wystarczy napisać pętlę która, zachowując ten warunek, w kolejnych obrotach "przerzuca" po jednej cyfrze z liczby p do liczby q, dążąc do "opróżnienia" (wyzerowania) liczby p.

def lustrzana(Z):
    p = Z
    q = 0
    while p != 0:
        # niezmiennik:
        #     czytając q wprost, a następnie p wspak, otrzymujemy liczbę lustrzaną do Z
        #     (zerową wartość p lub q traktujemy jako "brak cyfr")
        cyfra = p % 10
        p = p // 10
        q = q * 10
        q = q + cyfra
    # p==0, czyli w p "brak cyfr", 
    # zatem czytając samą liczbę q otrzymujesz całą liczbę lustrzaną do Z
    S = q
    return S

Zadanie 14

Pewien polski bank w ofercie na kwiecień 2009 miał produkt finansowy łączący cechy konta i lokaty. Środki bez karnych opłat można było podjąć tylko raz na miesiąc, ale za to oprocentowanie było bardziej korzystne, niż na zwykłym rachunku oszczędnościowo-rozliczeniowym. Oprocentowanie zależało od wysokości zgromadzonych środków. W kwietniu 2009 bank oferował oprocentowanie na następujących zasadach:

Odsetki są dopisywane miesięcznie. Wpłacamy kapitał początkowy (np. 49'400 PLN), ile miesięcy musimy czekać, zanim z konta da się wyjąć pewną określoną sumę (np. 50'500 PLN) ?

Dane: kapitał początkowy w zł, kapitał docelowy w zł (obie wartości podane jako liczby rzeczywiste dodatnie, z co najwyżej dwoma miejscami po przecinku).

Wynik: liczba miesięcy, po których kapitał początkowy wraz z odsetkami wystarczy do wypłacenia kapitału docelowego.

Zaproponuje algorytm i napisz program, który dla danego kapitału począkowego i końcowego oblicza, ile miesięcy trzeba poczekać na żądaną wypłatę.

Rozwiązanie:
Odpowiedź obliczymy symulując przyrost środków na koncie.

  za środki zgromadzone na koncie weź kapitał początkowy
  za zmienną m przyjmij zero
  dopóki środki zgromadzone na koncie < kapitał docelowy:
      powiększ środki zgromadzone na koncie o miesięczne odsetki
      powiększ m o jeden
  po m miesiącach z konta można wypłacić kapitał docelowy (być może z naddatkiem)

Program Lokata

def obliczOdsetkiMiesieczne(suma):
    assert 0 <= suma
    if suma < 50000: 
        return suma * 0.3675    # czyli 4.5% rocznie
    if suma < 100000: 
        return suma * 0.4074    # czyli 5.0% rocznie
    return suma * 0.4867        # czyli 6.0% rocznie
 
def zliczMiesiaceOszczedzania(kapitalPoczatkowy, kapitalDocelowy):
    assert 0 < kapitalPoczatkowy
    assert 0 < kapitalDocelowy
    srodki = kapitalPoczatkowy
    m = 0
    while srodki < kapitalDocelowy:
        odsetki = obliczOdsetkiMiesieczne(srodki)
        srodki = srodki + odsetki
        m = m + 1
    return m

Oto przykładowy ślad wykonania programu Lokata:

  zliczMiesiaceOszczedzania(kapitalPoczatkowy=49400.00, kapitalDocelowy=50500.00)
    assert(0 < kapitalPoczatkowy)                0 < 49400.00 → prawda
    assert(0 < kapitalPoczatkowy)                0 < 50500.00 → prawda
    srodki = kapitalPoczatkowy                   srodki = 50500.0
    m = 0
    while srodki < kapitalDocelowy               49500.00 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 181.9125
      srodki = srodki + odsetki                          srodki = 49681.9125
      m = m + 1                                     m = 1
    while srodki < kapitalDocelowy               49681.9125 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 182.581028
      srodki = srodki + odsetki                          srodki = 49864.493528
      m = m + 1                                     m = 2
    while srodki < kapitalDocelowy               49864.493528 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 183.252014
      srodki = srodki + odsetki                          srodki = 50047.745542
      m = m + 1                                     m = 3
    while srodki < kapitalDocelowy               50047.745542 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 203.894515
      srodki = srodki + odsetki                          srodki = 50251.640057
      m = m + 1                                     m = 4
    while srodki < kapitalDocelowy               50251.640057 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 204.725182
      srodki = srodki + odsetki                          srodki = 50456.365239
      m = m + 1                                     m = 5
    while srodki < kapitalDocelowy               50456.365239 < 50500.00 → prawda
      odsetki = odsetkiMiesieczne(srodki)        odsetki = 205.559232
      srodki = srodki + odsetki                          srodki = 50661.924471
      m = m + 1                                     m = 6
    while srodki < kapitalDocelowy               50661.924471 < 50500.00 → fałsz
    return m                                     → 6

-------------------------------------------------------------------------------------------------------------------------------------------------

Liczba \(p\) dzieli całkowicie \(q\), jesli tylko \(q\, \% p\, == 0\) (reszta z dzielenia \(q\) przez \(p\) jest równa 0). Każdą dodatnią liczbę całkowitą \(p\), która dzieli całkowicie \(q\) nazywamy dzielnikiem \(q\). Dzielnik nazywamy właściwym, gdy jest różny od 1 i od \(q\).

Dodatnią liczbę całkowitą nazywamy liczbą pierwszą, gdy jest różna od 1 i nie ma dzielników właściwych (dzieli się tylko przez 1 i samą siebie).

Zadanie 15

Każdą liczbę całkowitą różną od zera można zapisać jednoznacznie w postaci iloczynu liczby nieparzystej i liczby, która jest potęgą dwójki o nieujemnym, całkowitym wykładniku. Na przykład \(1 == 1*2^0,\, 24 == 3*2^3,\, 32 == 1*2^5,\, 80 == 5*2^4\).

Zmodyfikuj funkcję obliczania logarytmu dyskretnego z zadania 7 w taki sposób, żeby otrzymać funkcję Potega_2, której wartość dla danej dodatniej liczby całkowitej \(n\) jest równa potędze dwójki w opisanym iloczynie.

Zadanie 16

Napisz funkcję liczbaDzielnikow która dla danej dodatniej liczby całkowitej \(n\) wyznacza liczbę jej dzielników właściwych.

Wskazówka:

Przeglądaj kolejne liczby całkowite \(2, 3, \ldots n-1\) i zlicz te, które dzielą \(n\).

Rozwiązanie:

def liczbaDzielnikow(n):
    assert n >= 0
    k = 0
    dzielnik = 2
    while dzielnik < n: 
        if (n % dzielnik == 0):
            k = k + 1;
        dzielnik = dzielnik + 1;
    return k
}

Zadanie 17

Wykorzystaj funkcję z zadania 16 do napisania funkcji pierwsza, która sprawdza, czy dana dodatnia liczba całkowita jest liczbą pierwszą.

Rozwiązanie:

def pierwsza(n):
    assert n > 0
    if n == 1:
        return False
    else:
        return liczbaDzielnikow(n) == 0
} 

Zadanie 18

Każdą dodatnią liczbę całkowitą większą od 1 można przedstawić w postaci iloczynu liczb pierwszych: \(2 = = 2;\, 3 = = 3;\, 4 = = 2*2;\, 5 = = 5;\, 6 = = 2*3;\, 24 = = 2*2*2*3\). W tabeli poniżej przypominamy szkolny algorytm rozkładu zdanej liczby całkowitej na czynniki pierwsze.

Zaadoptuj algorytm szkolny i napisz funkcję liczbaCzynnikow, która dla danej liczby całkowitej \(n > 1\) obliczy liczbę jej czynników pierwszych.

Zadanie 19

Wykonaj zadanie podobne do zadania 18, tylko tym razem napisz funkcję liczbaRoznychCzynnikow zliczającą różne czynniki pierwsze. Na przykład, w rozkładzie liczby 924=2*2*3*7*11 występują 4 różne czynniki pierwsze.

Rozwiązanie:

def liczbaRoznychCzynnikow(n):
    assert n > 1
 
    czynnik = 2
    ostatniCzynnik = 1
    licznik = 0
    m = n
 
    while m != 1: 
        if m % czynnik == 0:
            if czynnik != ostatniCzynnik:
                licznik = licznik + 1
                ostatniCzynnik = czynnik
            m = m / czynnik
        else:
            czynnik = czynnik + 1
    return licznik