Iteracja II

Komputerowy skład czytelnych i estetycznych tabel to złożony problem, nad rozwiązaniem którego głowią się twórcy specjalizowanych programów (np. takiego jak LaTeX). Przykładem bardzo prostego zadania pojawiającego się przy okazji składu tabel jest wyznaczenie szerokości komórki tabeli na podstawie zawartej w niej wartości liczbowej. W maksymalnym uproszczeniu, chcielibyśmy dla danej liczby naturalnej obliczyć, ile cyfr zajmie jej reprezentacja dziesiętna.

Zadanie cyfry dzisiętne

Dane: liczba naturalna n.

Wynik: liczba cyfr liczby n w zapisie dziesiętnym.

Dozwolone operacje: porównania, operacje arytmetyczne.

Interesująca nas funkcja powinna dawać m.in. takie wyniki:

cyfryDziesiętne(2009) -> 4
cyfryDziesiętne(15) -> 2
cyfryDziesiętne(7) -> 1
cyfryDziesiętne(0) -> 1

Na pierwszy rzut oka wydaje się, że wystarczy policzyć ile razy daną liczbę da się podzielić przez dziesięć (każde całkowite dzielenie przez dziesięć "przesuwa" cyfry w prawo, gubiąc cyfrę "wypadającą" za przecinek dziesiętny).

def cyfryDziesietne(n):
    licznik = 1
    while n // 10 != 0:
        n =  n // 10
        licznik = licznik + 1
    return licznik

Niby dobrze, ale trochę dziwnie wygląda, że dzielenie przez 10 występuje w dwóch miejscach. Moglibyśmy przeformułować algorytm w ten sposób:

1. zlicz jedną cyfrę
2. n = n // 10
3. jeżeli "zostały jeszcze jakieś cyfry w n" (tzn. jeżeli n!=0), powtórz od punktu 1.

Tylko że nie bardzo wiadomo, jak go zapisać za pomocą pętli while. Pętla while zawsze sprawdza dozór przed wykonaniem obrotu pętli, natomiast w powyższym opisie sprawdzenie dozoru chcielibyśmy przeprowadzić po wykonaniu obrotu pętli.

Pętla do-while

Języki programowania oferują różne udogodnienia na tym polu. Np. język C++ posiada pętlę do-while, która sprawdza dozór po obrocie pętli:

int licznik = 0
do {
    licznik = licznik + 1;
    n = n / 10;
} while (n != 0);

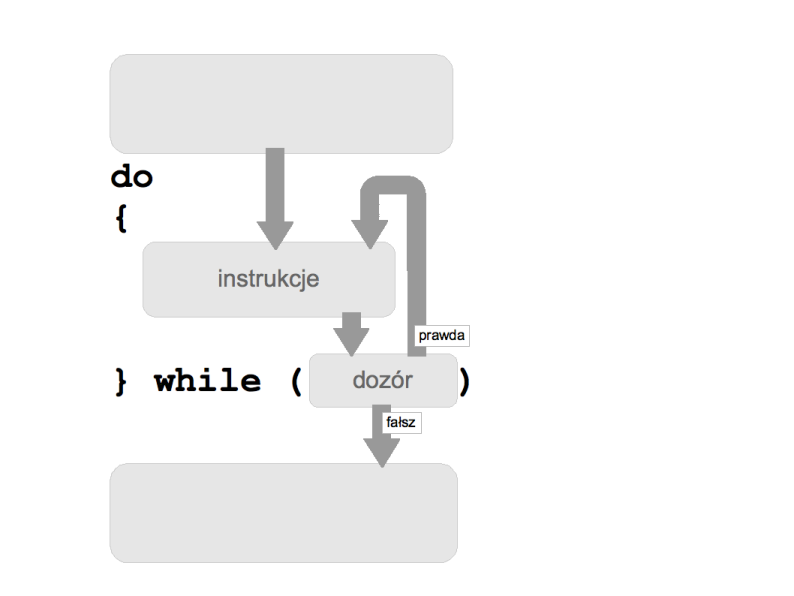
Język Python nie posiada instrukcji pętli do-while.

Instrukcja break

Innym rozwiązaniem jest instrukcja 'break' powodująca przerwanie wykonania pętli. W tym przypadku moglibyśmy skorzystać z instrukcji 'break' wstawionej w tzw. wieczną pętlę, której dozór jest zawsze prawdziwy:

licznik = 0
while True:
    licznik = licznik + 1
    n = n // 10
    if n == 0: break
return licznik

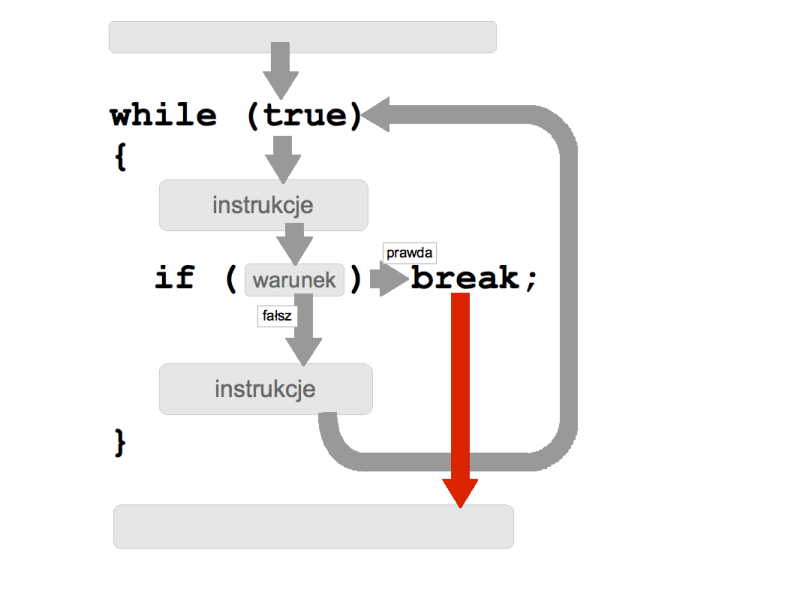
W tej wersji dziwnie wygląda inicjacja licznika wartością zero, bo w pierwszym obrocie pętli zaraz po przypisaniu zera licznik jest bezwarunkowo zwiększany o jeden. Czy nie da się zapisać tego kodu w ten sposób, by od razu inicjować licznik wartością 1? W tym przypadku możemy obrócić instrukcje pętli i wyciągnąć jedną kopię operacji zwiększania licznika przed pętlę:

licznik = 0
licznik = licznik + 1
while True:
    n = n // 10
    if n == 0: break
    licznik = licznik + 1
return licznik

Dwie pierwsze instrukcje możemy teraz zamienić na jedną instrukcję przypisania:

licznik = 1
while True:
    n = n // 10
    if n == 0: break
    licznik = licznik + 1
return licznik

Wyjście z pętli poprzez wyjście z funkcji

Powyższą funkcję można jeszcze uprościć, korzystając z faktu, że bezpośrednio po wyjściu z pętli następuje wyjście z funkcji. Ponieważ pomiędzy wykonaniem instrukcji break, a wykonanie instrukcji return nic ważnego się nie dzieje, możemy po prostu od razu posłużyć się instrukcją return:

licznik = 1
while True:
    n = n // 10
    if n == 0: return licznik
    licznik = licznik + 1

ZADANIA

Zadanie 1

Każdą liczbę naturalną można przedstawić jako iloczyn liczb pierwszych. W tym zadaniu zajmiemy się liczbami, których czynnikami pierwszymi są wyłącznie dwójki i trójki. Innymi słowy, taka interesująca nas liczba daje się przedstawić jako iloczyn pewnej potęgi dwójki oraz pewnej (niekoniecznie tej samej) potęgi trójki (mówimy tylko o potęgach o wykładnikach naturalnych). Takie liczby będziemy nazywać 2-3-mieszanymi. Oto 10 najmniejszych liczb 2-3-mieszanych:

\( 1 == 2^0*3^0; 2 == 2^1*3^0; 3 == 2^0*3^1; 4 == 2^2*3^0; 6 == 2^1*3^1; 8 == 2^3*3^0;\)
\(9 == 2^0*3^2; 12 == 2^2*3^1; 16 == 2^4*3^0; 18 == 2^1*3^2 . \)

Napisz program, który dla danej, dodatniej liczby naturalnej \(n\) policzy najmniejszą liczbę 2-3-mieszaną większą od \(n\).

Dokładna specyfikacja tego zadania jest następująca.

Dane: dodatnia liczba całkowita \(n\).

Wynik: najmniejsza liczba 2-3 mieszana większa od \(n\).

Rozwiązanie:

Proponujemy rozwiązanie naturalne - wyznaczamy kolejnych kandydatów do wyniku i spośród nich wybieramy najmniejszego. Przeglądanie kandydatów zaczynamy od najmniejszej potęgi dwójki większej od \(n\). Niech tą liczbą będzie \(2^r\). Kolejni kandydaci będą mieli postać \(2^i*3^{q_i}\), gdzie \(i == r-1, r-2,\ldots, 0\), a \(q_i\) jest najmniejsze takie, że \(2^i*3^{q_i} > n\). Do wyznaczenia liczby \(2^r\) i kolejnych kandydatów posłużymy się pętlą while.

def minPotegaDwojkiWiekszaOd(n):
    assert n >= 1
    p = 1
    while p <= n:
        p *= 2
    return p

Wynik funkcji minPotegaDwojkiWiekszaOd(n) daje nam pierwszego kandydata do obliczenia wyniku. W kolejnych krokach będziemy rozważali liczby

minPotegaDwojkiWiekszaOd(n) / 2¹
minPotegaDwojkiWiekszaOd(n) / 2²
minPotegaDwojkiWiekszaOd(n) / 2³
...

i każdą z nich mnożyli tyle razy przez 3, żeby dostać liczbę większą od \(n\) - to nasi kandydaci, z których musimy wyznaczyć najmniejszego. Opisana idea jest zrealizowana w funkcji \(minDwaTrzyMieszanaWiekszaOd(n)\).

def minDwaTrzyMieszanaWiekszaOd(n):
    assert n >= 1
    potegaDwojki = minPotegaDwojkiWiekszaOd(n)
    minMieszana = potegaDwojki
    while True:
        potegaDwojki = potegaDwojki//2
        mieszana = potegaDwojki
        while True:
            mieszana = mieszana*3
            if mieszana > n: break
        minMieszana = min(minMieszana, mieszana)
        if potegaDwojki == 1: break
    assert potegaDwojki == 1
    return minMieszana

Zastanowimy się teraz, czy nie można wyeliminować wewnętrznej pętli. Rozważmy wartości zmiennej mieszana obliczane w wyniku wykonania pętli wewnętrznej. Te wartości są liczbami 2-3-mieszanymi. Przyjmijmy, że po jednym wykonaniu pętli wartość mieszana jest postaci \(2^x*3^y\) (z faktu, że jest to liczba 2-3-mieszana wynika, że zawsze znajdą się odpowiednie wartości x i y). Ile wynosi wartość tej zmiennej po wykonaniu następnego obrotu pętli zewnętrznej (czyli po ponownym wykonaniu pętli wewnętrznej)? Jest nią \(2^{x-1}*3^y\), gdy ta wartość jest większa od \(n\), i \(2^{x-1}*3^{y+1}\), gdy \(2^{x-1}*3^y \le n\). Jest tak dlatego, ponieważ \(2^{x-1}*3^{y+1} > 2^x*3^y\). Biorąc to pod uwagę, instrukcje zewnętrznej pętli możemy zapisać tak:

  // mieszana = 2_x * 3_y
  mieszana = mieszana//2
  if mieszana <= n:
      mieszana = mieszana*3
  minMieszana = min(minMieszana, mieszana)

Teraz jeszcze raz cała funkcja, tylko musimy pamiętać o tym, że wartości zmiennej mieszana liczymy inaczej.

def minDwaTrzyMieszanaWiekszaOd(n):
    potegaDwojki = minPotegaDwojkiWiekszaOd(n)
        # potegaDwojki == 2<sup>x</sup>
        # x jest najmniejsza liczba dajaca 2<sup>x</sup> > n
    mieszana = potegaDwojki
        // mieszana == potegaDwojki * 3<sup>0</sup>
    while True:
        # mieszana == potegaDwojki * 3<sup>y</sup>
        #     gdzie y jest najmniejszą liczbą
        #     dającą  potegaDwojki * 3^y > n
        potegaDwojki = potegaDwojki//2
        mieszana = mieszana//2
        if mieszana <= n:
            mieszana = mieszana*3
        minMieszana = min(minMieszana, mieszana)
        if potegaDwojki == 1: break
    assert potegaDwojki == 1
    return minMieszana

Zauważmy, że w powyższej funkcji zmienna potegaDwojki służy nam tylko po to, żeby wiedzieć kiedy zakończyć wykonywanie pętli (i do zapisania warunków w logicznych w komentarzach). Gdy potegaDwojki == 1, to wartość zmiennej mieszana jest nieparzysta, natomiast gdy potegaDwojki > 1, wartość zmiennej mieszana jest parzysta (innej możliwości nie ma, potegaDwojki nigdy nie przyjmuje wartości mniejszych od 1). Wykorzystamy to w sformułowaniu dozoru pętli.

def minDwaTrzyMieszanaWiekszaOd(n):
    mieszana = minPotegaDwojkiWiekszaOd(n)
    minMieszana = mieszana
    while True:
        mieszana = mieszana//2
        if mieszana <= n:
            mieszna *= mieszana*3
        minMieszana = min(minMieszana, mieszana)
        if not parzysta(mieszana): break
    return mieszana

Zadanie 2

Pokaż w jaki sposób wyrazić pętlę

do instrukcje while (warunek);

za pomocą pętli

while (warunek) do instrukcje;

Rozwiązanie:

instrukcje; while warunek(W) do instrukcje

Zadanie 3

Ułóż algorytm, który dla dodatniej liczby naturalnej \(n\) obliczy iloma zerami kończy się zapis dziesiętny liczby \(1*2*\ldots*n\). Na przykład, dla \(n == 10\) wynikiem jest 2, ponieważ \(1*2*3*4*5*6*7*8*9*10 == 3628800.\)

Wskazówka:

Policz sprytnie ile jest 2 i ile jest 5 w rozkładzie \(1*2*\ldots*n\) na czynnik pierwsze. Mniejsza z tych liczb jest poszukiwaną odpowiedzią.